摆线针轮齿廓修形参数对摩擦润滑接触特性的影响*

孙章栋 梅 涵 任爱华 王红霞

(湖北汽车工业学院汽车动力传动与电子控制湖北省重点实验室 湖北十堰 442002)

摆线针轮传动以结构紧凑、传动比大和使用周期长等优点而广泛应用于汽车、建筑、石油、纺织等行业。摆线针轮传动同时啮合齿数理论上可以达到一半的摆线轮齿数，但实际上为了补偿制造与安装误差，摆线针轮在加工过程中必须进行合理修形，使摆线轮在齿根与齿顶位置与针齿存在顶隙。修形后的摆线针轮传动同时啮合齿数减少，承载能力及传动精度也随之发生变化。

本文作者基于Ostwald模型建立摆线针线接触润滑数值模型，研究摆线针轮修形参数对其摩擦润滑接触特性的影响规律。研究结果对工程实际中摆线针轮脂润滑问题有一定指导意义。

1 啮合分析

摆线针轮传动同时啮合的齿数多，但实际上为保证补偿制造误差、可靠润滑和装拆方便，摆线轮齿面在磨齿时必须进行合理的修形，使同时啮合齿数减少，达不到理论所说的一半齿数，并且会增加传递误差。常用的修形方法有3种，即移距修形、等距修形以及两者组合修形。如图1所示，在啮合过程中，摆线轮曲率半径ρ变化，针齿半径rz为定值，从而可得啮合过程中的当量曲率半径和载荷分别为

R=ρrz/(ρ±rz)

(1)

(2)

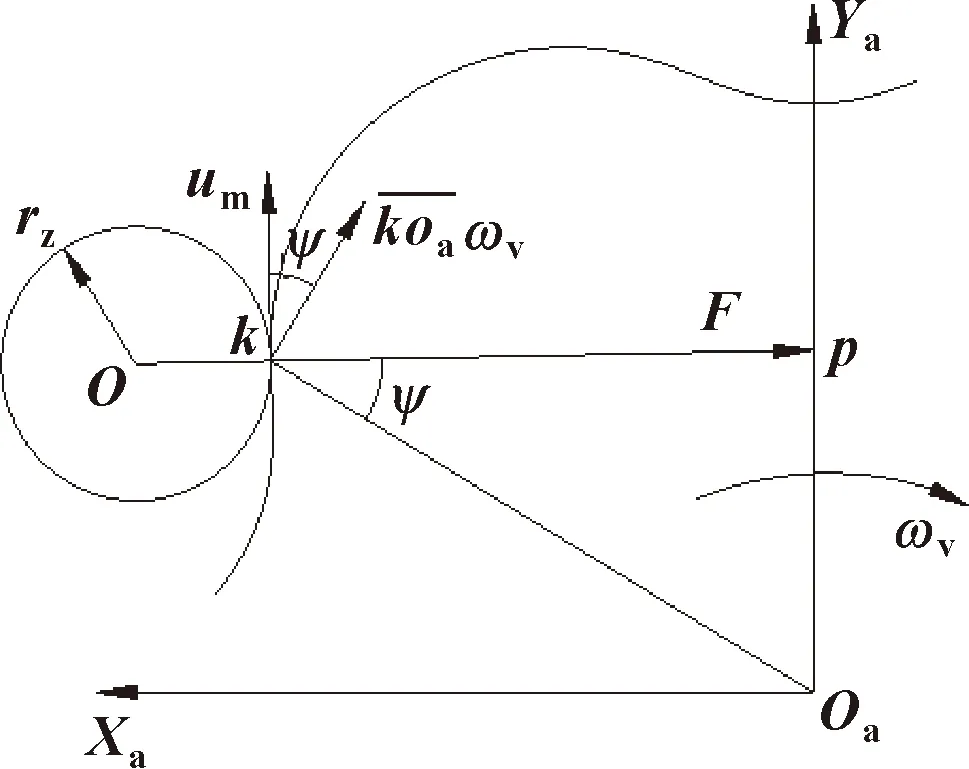
图1 摆线轮与针齿啮合示意Fig.1 The meshing of cycloid gear with needle teeth

由运动学分析可知，摆线轮与针齿在啮合点处的线速度是相等的，滑动速度为0。由图1所示，对润滑油的卷吸速度为

(3)

2 摩擦润滑接触模型

基于Ostwald模型的润滑脂本构方程[15]为

(4)

式中：m为黏性函数；n为脂润滑液流变指数。

如果采用Roelands方程，黏性函数可表示为

m=m0exp{(lnm0+9.67)[(1+1.98×10-8p)z0-1]×[(T-138)/(T0-138)]-s}

(5)

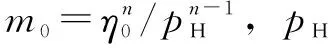
采用广义Reynolds方程[13]，引入等效黏度η*，对于Ostwald模型，其等效黏度为

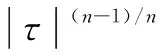
(6)

利用Hertz接触参数对润滑模型进行量纲一化，量纲一化公式为

式中：x为流动方向；z为膜厚方向；b为Hertz接触半宽；h为油膜厚度；p为油膜压力；R为等效曲率半径；η0为润滑油环境黏度；E为等效弹性模量；t为时间。

量纲一化Reynolds方程[13]为

(7)

其中

式中：ρ0为润滑油环境密度。

量纲一化Reynolds方程的边界条件为

(8)

式中：Xin和Xout分别为润滑接触入口边界和出口边界。

油膜的量纲一化能量方程为

(9)

固体的量纲一化能量方程为

(10)

量纲一化的膜厚方程、Dowson-Higginson密度方程、载荷方程，油膜量纲一化能量方程和固体量纲一化能量方程边界条件可参考文献[14-16]。离散量纲一化Reynolds方程[17]为如下形式：

αipi-1+βipi+γipi+1=δi

(11)

式中：αi、βi、γi和δi为Poiseuille流、Couette流和Squeeze流差分系数的和。

离散成式(11)的形式方便在压力迭代过程中利用追赶法求解压力。文中利用二阶中心差分离散Poiseuille流，一阶向后差分离散Couette流和Squeeze流。

二阶中心差分离散Poiseuille流：

(12)

其中

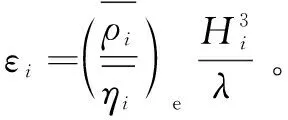
则二阶中心差分格式的Poiseuille流各系数可写为

(13)

一阶向后差分离散Couette流：

(14)

则构成Couette流线性方程各系数可写为

(15)

一阶向后差分离散Squeeze流：

(16)

则构成Squeeze流线性方程各系数可写为

(17)

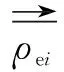
离散量纲一化Reynolds方程差分系数如下：

(18)

温度求解与压力求解相似，利用追赶法求解。量纲一化计算域范围X=[Xin,Xout]=[-4,1.5],油膜厚度量纲一化计算范围Z=[0,1]，固体计算范围Z1=Z2=[0,3.15]。X方向的节点数1 025，油膜厚度Z向节点数11。一个针齿与一个摆线轮齿的啮合相位角180°作为一个计算周期，把该计算周期分为241个瞬时进行计算。求解瞬态热弹流过程均包括压力和温度的分别求解，压力和温度求解需交替进行。上一瞬时压力和温度作为当前瞬时迭代的初始值，第一瞬时迭代的初始压力和温度分别为Hertz压力和环境温度。压力、载荷和温度数值迭代精度分别为

|∑|Pi|-(π/2)|/(π/2)<0.000 01

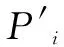
弹流润滑分析中计算接触副摩擦因数，采用两接触线上剪切力均值与载荷比值。

1.2.2 保脾手术 生物胶合止血、物理凝固止血和单纯缝合修补3例,脾修补加脾动脉结扎术3例。脾部分切除2例。

(19)

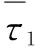
弹流润滑分析中计算接触副摩擦功率损失为：该接触点沿膜厚方向剪切力与膜厚层之间滑动速度的乘积并沿膜厚积分[18]。

(20)

整个接触区域的滚动摩擦功率损失为

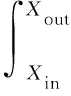
(21)

整个啮合区间总的滚动摩擦功率损失为

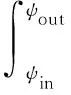
(22)

式中：ψin和ψout分别为啮合起始相位角和退出相位角。

3 结果与讨论

摆线轮主要采用4种修形方式，即负移距修形、正等距修形、正等距+正移距修形和负等距+负移距修形。修形量一定情况下，采用正等距修形承载能力优于负移距修形，但是传递误差较大；从高承载能力优化目标出发，来确定正等距修形量和正移距修形量，故正等距+正移距修形方法承载能最优；从高精度齿形优化目标出发，确定负等距修形量和负移距修形量，因此负等距+负移距修形传递误差最小。根据摆线齿轮减速器加工精度确定顶隙为0.1 mm，进一步确定等距修形量和移距修形量。选取摆线针轮行星传动啮合副为研究对象，其啮合副与润滑相关参数见表1。考虑制造与安装误差的影响，摆线轮与针齿之间的滑滚比设为0.2。

表1 摆线针轮传动副与润滑相关参数Table 1 The parameters of the cycloid gear pair and lubrication

摆线轮与针齿滚动线接触啮合，在啮合过程中，单位啮合力F、等效曲率半径和卷吸速度随着啮合相位变化。图2给出了标准理论齿廓与顶隙为0.1 mm条件下4种修形方式的单位啮合力、卷吸速度和等效曲率半径随啮合相位变化曲线，在相位ψ=arccosK1处为曲线拐点。可以看出：修形齿廓啮合区间相对标准齿廓缩小；在修形齿廓中，正等距+正移距组合修形啮合区间最大，负等距+负移距组合修形啮合区间最小，正等距单修形方式的啮合区间大于负移距单修形方式；修形齿廓的啮合力在相位角ψ=arccosK1附近处大幅增加，等效半径及卷吸速度在重合啮合区间与标准齿廓近似吻合。

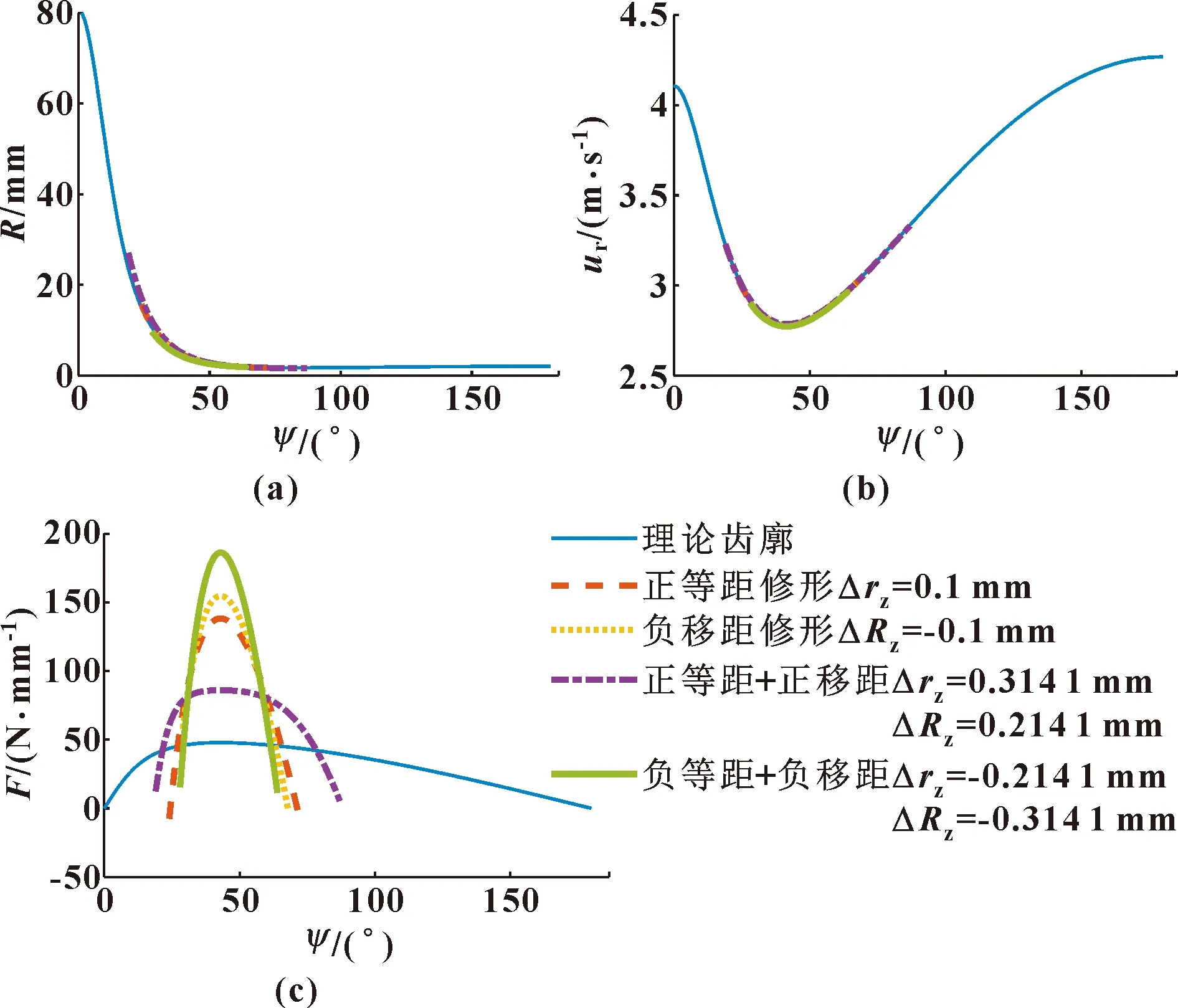
图2 标准理论齿廓与4种修形方式下等效曲率半径(a)、卷吸速度(b)、单位啮合力(c)随啮合相位变化Fig.2 Variation of equivalent radius(a),rolling speed(b)and contact force(c) with meshing process for thestandard profile and the four types of the modification

为验证数值模型的正确性，图3给出了顶隙为0.1 mm条件下正等距+正移距组合修形齿廓最小膜厚数值解与经验公式计算结果的比较。当Ostwald流体流变指数为1时表现出牛顿流体特征。

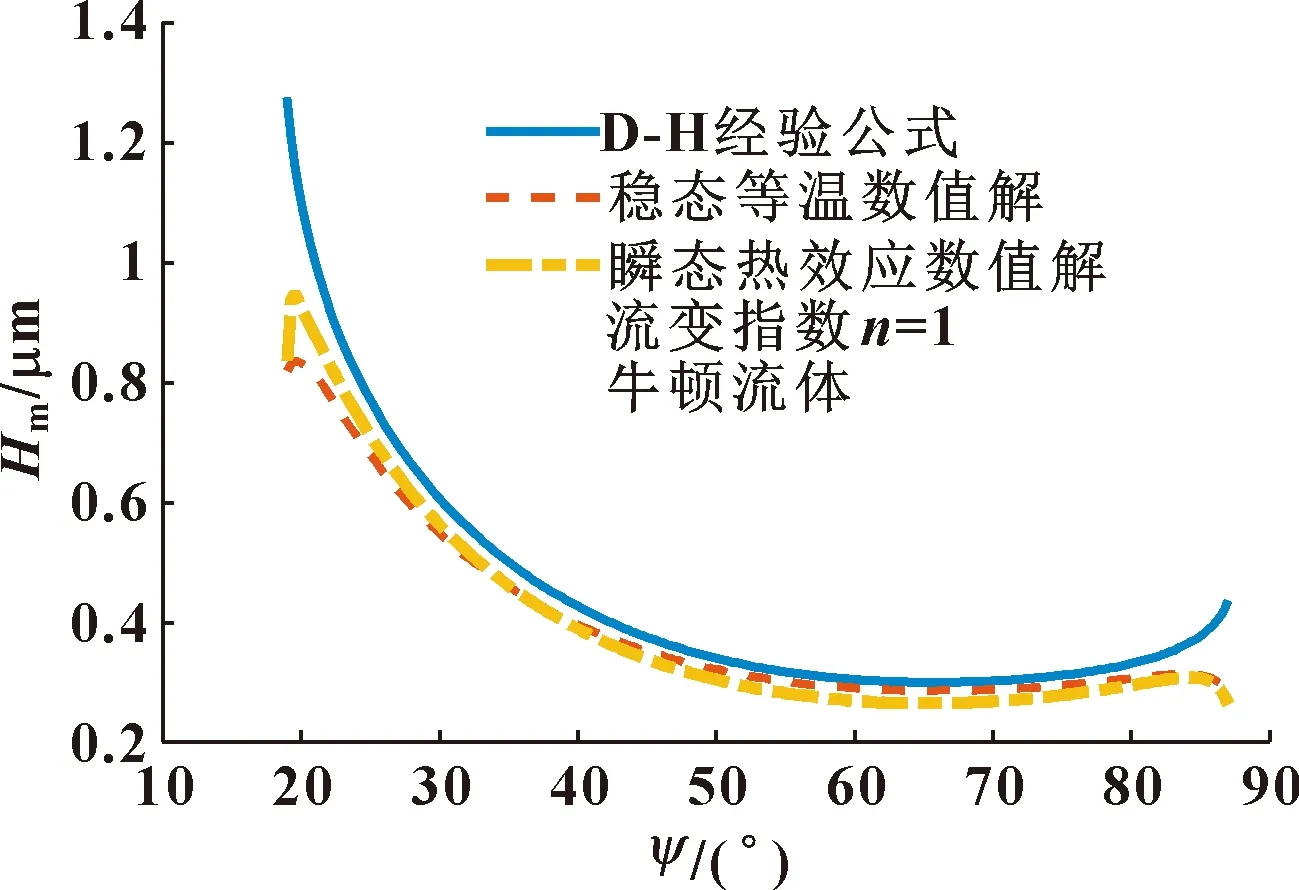
图3 正等距+正移距组合修形齿廓最小膜厚数值解与经验公式计算值比较Fig.3 Comparison between the minimum film thickness numericalsolution of the modification tooth profile with combinedpositive equidistant and positive radial-moving schemeand the calculation results of empirical formula

图3表明：修形齿廓最小膜厚稳态等温数值解与采用Dowson-Higginson润滑油膜厚经验公式计算结果变化趋势相吻合，但经验公式计算出的膜厚值偏大。修形齿廓最小膜厚瞬态数值解与稳态数值解变化趋势一致，在啮合相位初始阶段最小膜厚瞬态数值解较稳态数值解计算结果大。随着啮合相位增加，瞬态数值解不断减小，在某一啮合相位处先与稳态解计算结果相等，在啮合相位结束阶段小于稳态解。

3.1 不同修形方式对摩擦润滑状态的影响

为了研究不同修形方式对摆线轮齿廓摩擦润滑接触状态的影响，图4给出了顶隙为0.1 mm条件下不同修形方式下啮合过程中的中心压力和最小油膜厚度变化曲线。在大部分啮合区间内，负等距+负移距组合修形方式得到的中心压力最大、最小油膜厚度最小，正等距+正移距组合修形方式得到的中心压力最小、最小油膜厚度最大；负移距单修形方式得到的中心压力比正等距单修形方式大，最小油膜厚度比正等距单修形方式小。

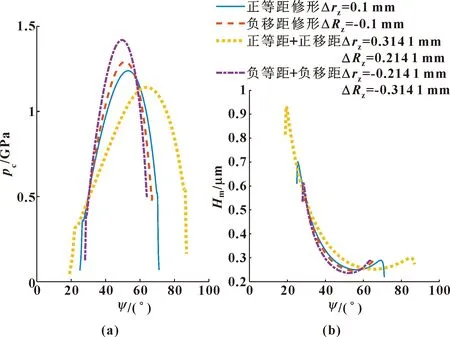
图4 不同修形方式下啮合过程中中心压力(a)及最小油膜厚度(b)变化Fig.4 Variation of the central pressure(a) and theminimum film thickness(b) in the meshingprocess with different modification schemes

图5(a)、图5(b)分别给出了不同修形方式下修形齿廓啮合过程中摩擦因数和摩擦损失功率变化曲线。图中每个相位的摩擦因数和摩擦损失功率由式(19)、(20)、(21)计算得到。可以看出，在大部分重合啮合区间内，负等距+负移距修形方式得到的摩擦因数和摩擦损失功率最大，正等距+正移距修形方式得到的摩擦因数和摩擦损失功率最小，负移距单修形方式得到的摩擦因数和摩擦损失功率比正等距单修形方式大。这主要是由于不同修形方式引起啮合过程中载荷变化，从而导致啮合过程中摩擦因数和摩擦损失功率发生变化，如图2所示。

为比较一个啮合周期内整个啮合过程中不同修形方式下产生的摩擦损失功率情况，图5(c)给出了不同修形方式整个啮合过程中总的摩擦损失功率(由式(22)计算得到)。可以看出，正等距+正移距修形方式整个啮合过程中总的摩擦损失功率值最小，负等距+负移距修形方式的摩擦损失功率值最大，负移距单修形方式整个啮合过程中总的摩擦损失功率大于正等距单修形方式的值。

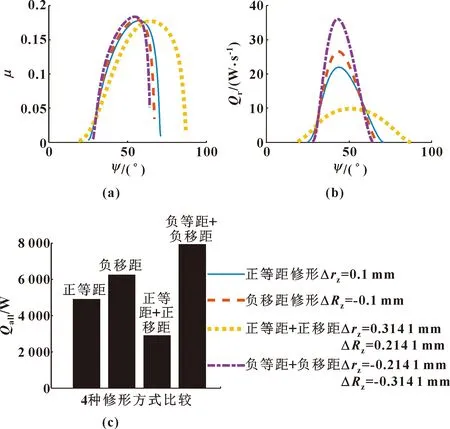
图5 不同修形方式下啮合过程中摩擦因数(a)、摩擦损失功率(b)及整个啮合过程中总的摩擦损失功率(c)变化Fig.5 Variation of friction coefficient(a) and rolling powerloss(b) in the meshing process and the totalrolling power loss(c) for the whole meshingprocess with different modification schemes

为进一步对4种修形方式下摩擦润滑状态进行评价，图6给出了不同修形方式下修形齿廓在啮合相位角ψ=arccosK1处润滑脂膜压力及油膜厚度分布曲线；图7给出了不同修形方式下修形齿廓在啮合相位角ψ=arccosK1处两固体表面平均剪切力、膜厚方向上平均速度变化率及摩擦损功率变化曲线。综合分析表明，正等距+正移距修形方式啮合过程中摩擦润滑状态最优，负等距+负移距修形方式摩擦润滑状态最差，正等距单修形方式摩擦润滑状态优于负移距单修形方式。

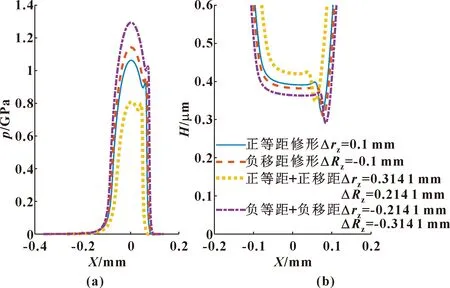
图6 不同修形方式下相位角θ=arccosK1处压力(a)及膜厚(b)变化

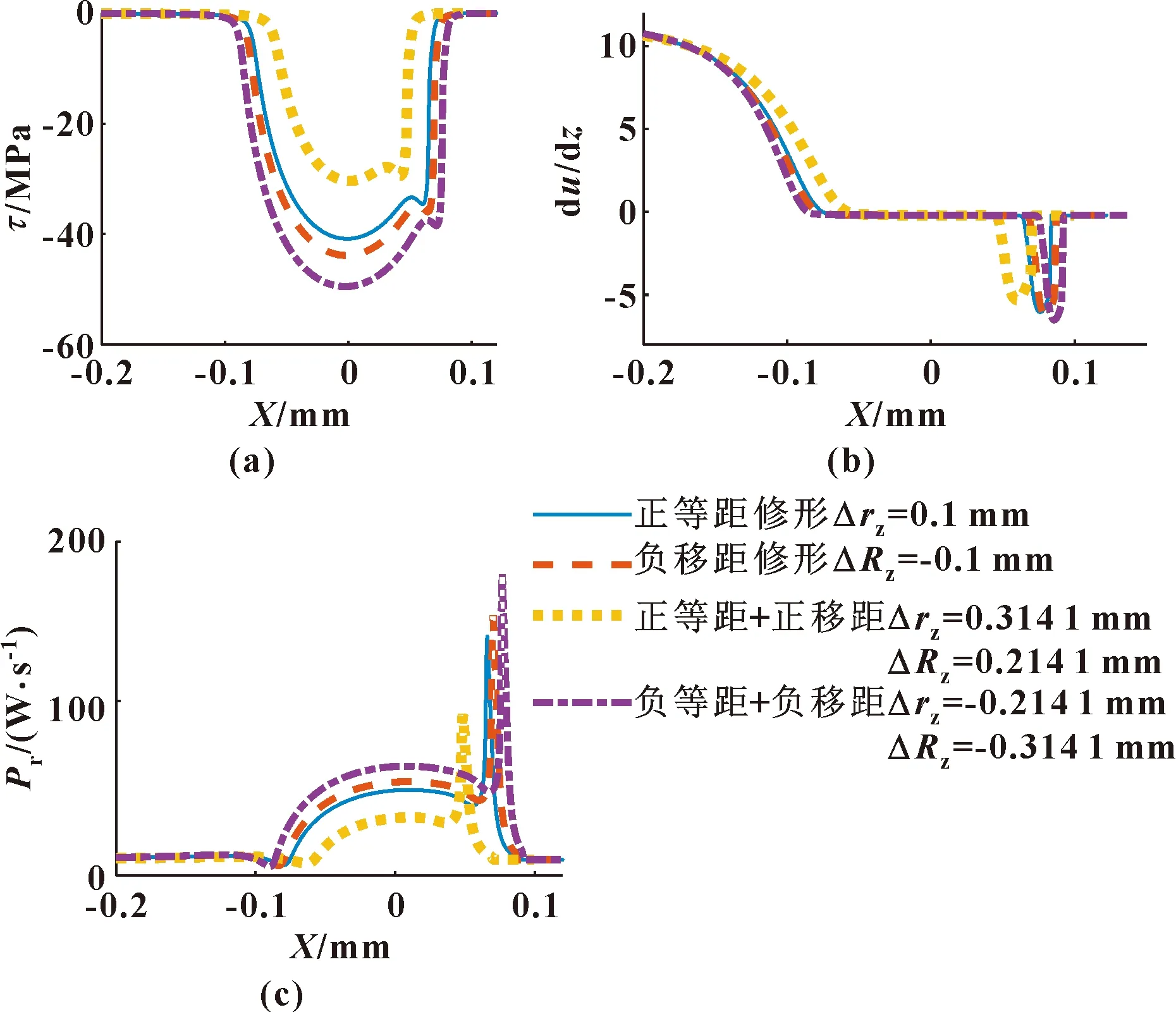
图7 不同修形方式下相位角ψ=arccosK1处两固体表面平均剪切力(a)、膜厚方向上平均速度变化率(b)及摩擦损功率(c)变化Fig.7 Variation of average shear stress(a) of the two interfaces,average sliding velocity(b) along the film thicknessdirection and rolling power loss(c) at the phase θ=arccosK1 for different modification schemes

3.2 修形量变化对摩擦润滑状态的影响

前面分析表明，负移距修形方式会引起修形齿廓摩擦润滑接触状态变差。下文讨论负移距单修形方式下修形量变化对摩擦润滑接触的影响。根据不同顶隙确定不同的移距修形量，图8给出了负移距单修形方式下修形量变化对啮合过程中中心压力及最小油膜厚度的影响，图9给出了负移距单修形方式下修形量变化对啮合过程中的摩擦因数、摩擦损失功率及整个啮合过程中总的摩擦损失功率的影响。图8表明，随着负移距修形量增加，啮合区间减小，大部分啮合区间中心压力增大，大部分啮合区间膜厚减小。如图9(a)、9(b)所示，随着负移距修形量增加，大部分啮合区间摩擦因数略微增大，大部分啮合区间摩擦损失功率增大。如图9(c)所示，随着负移距修形量增加，整个过程总的摩擦损失功率增加。

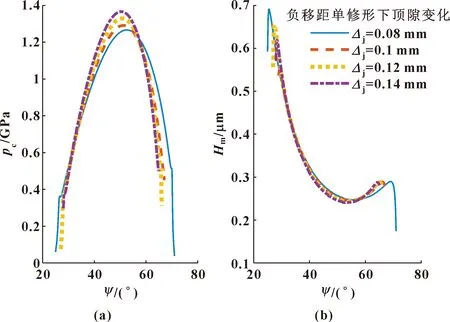
图8 负移距单修形方式下修形量对啮合过程中中心压力(a)及最小油膜厚度(b)的影响Fig.8 Effect of the amount of the single negative radial-movingmodification on the central pressure(a) and theminimum film thickness(b) in the meshing process

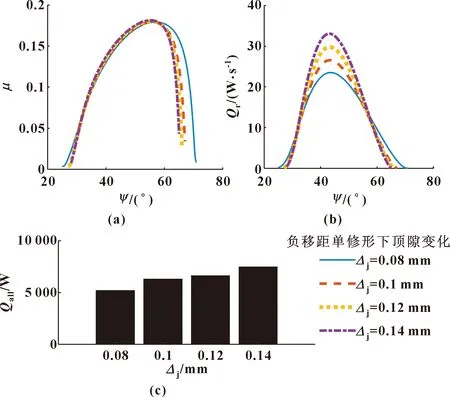
图9 负移距单修形方式下修形量对啮合过程中摩擦因数(a)、摩擦损失功率(b)及整个啮合过程中总的摩擦损失功率(c)的影响Fig.9 Effect of the amount of the single negative radial-moving modification on the friction coefficient(a),rolling power loss(b) and the total rolling powerloss(c) for the whole meshing process

图10、图11给出了组合正等距+正移距组合修形方式下修形量变化对啮合过程中中心压力、最小膜厚、摩擦因数、摩擦损失功率及整个啮合过程中总的摩擦损失功率的影响。图中结果进一步说明随着修形量增加，大部分啮合区间膜厚减小，大部分啮合区间摩擦因数略微增大，摩擦损失功率增大，整个啮合过程总的摩擦损失功率增加，摩擦润滑状态变差。

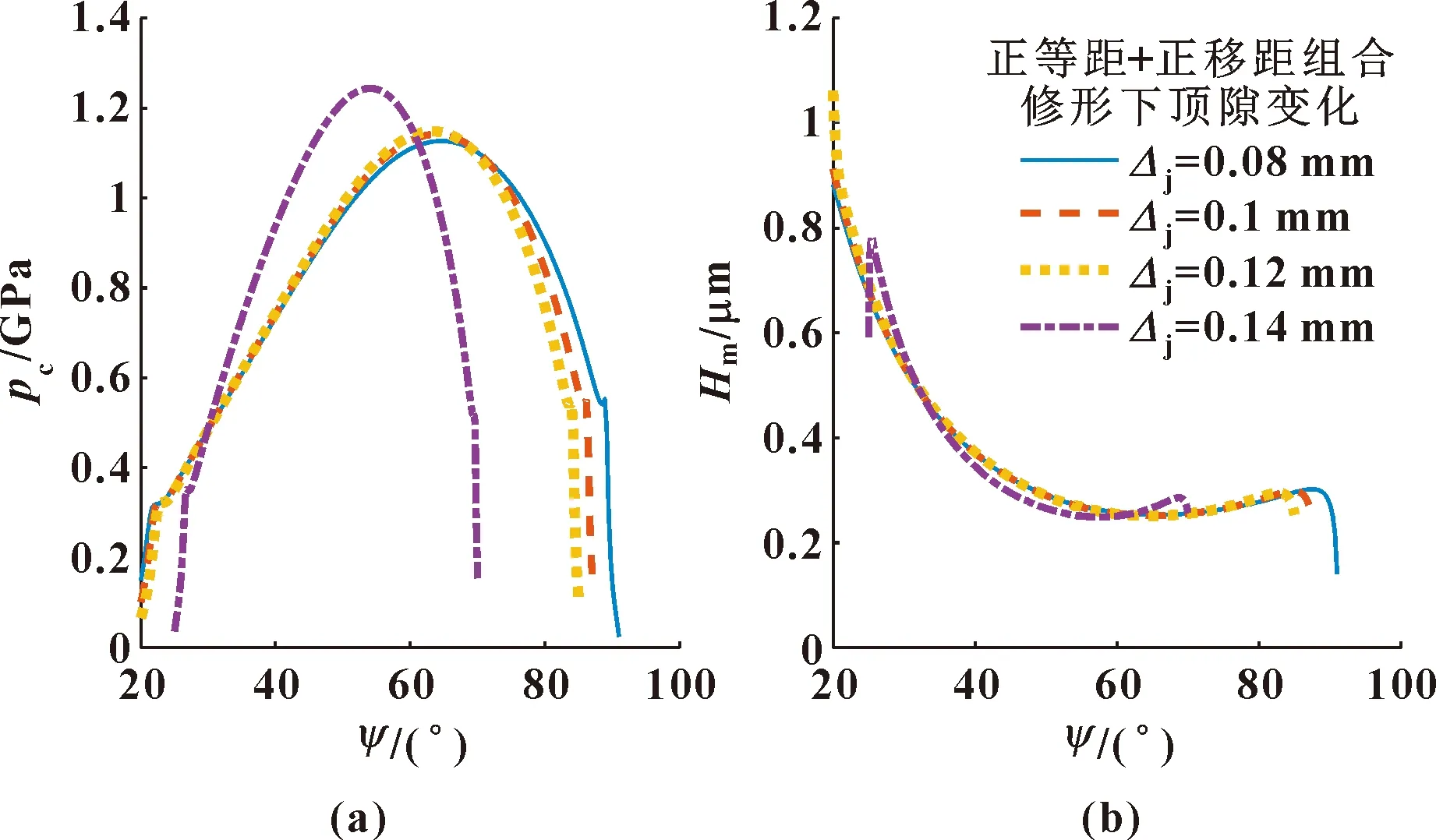
图10 组合修形方式下修形量对啮合过程中中心压力(a)及最小油膜厚度(b)的影响Fig.10 Effect of the amount of the combined modification onthe central pressure(a) and the minimum filmthickness(b) in the meshing process

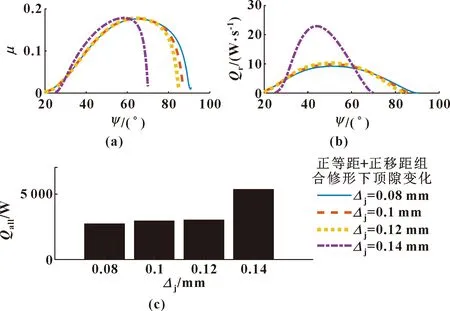
图11 组合修形方式下修形量对啮合过程中摩擦因数(a)、摩擦损失功率(b)及整个啮合过程中总的摩擦损失功率(c)的影响Fig.11 Effect of the amount of the combined modification on thefriction coefficient(a),rolling power loss(b) and the totalrolling power loss(c) for the whole meshing process

3.3 转速变化对摩擦润滑状态的影响

转矩变化会影响修形量变化，修形量变化对摩擦润滑状态的影响前面已分析，在此只讨论转速变化对摩擦润滑状态的影响。图12给出了正等距+正移距组合修形方式下转速变化对啮合过程中最小油膜厚度、摩擦因数、摩擦损失功率及整个啮合过程中总的摩擦损失功率的影响。可以看出，随着转速增加，啮合过程中最小油膜厚度增大、摩擦因数减小、摩擦损失功率增大、总的摩擦损失功率增加。这主要是由于转速增加有利于形成油膜，故膜厚增加；速度增加导致油膜温度增加，润滑油黏度降低，故摩擦因数降低，剪切力降低；但油膜厚度方向的速度变化率会增加，当油膜厚度方向的速度变化率增加值大于剪切力降低值时，两者乘积在油膜厚度增加的情况下积分就导致摩擦损失功率增大。

图12 正等距+正移距组合修形方式下转速变化对啮合过程最小膜厚(a)、摩擦因数(b)、摩擦损失功率(c)及整个啮合过程中总的摩擦损失功率(d)的影响Fig.12 Effect of the various input speeds on the minimumfilm thickness(a),friction coefficient(b),rollingpower loss(c) and the total rolling power loss(d)for the combined positive equidistant with positiveradial-moving modification

图13给出4种修形方式下啮合过程中总的摩擦损失功率随转速变化曲线。随着转速增加，不同修形方式下啮合过程中总的摩擦损失功率都线性增加，正等距+正移距组合修形啮合过程中总的摩擦损失功率在不同转速下始终最小，负等距+负移距组合修形啮合过程中总的摩擦损失功率始终最大，负移距单修形下总的摩擦损失功率大于正等距单修形方式下总的摩擦损失功率。

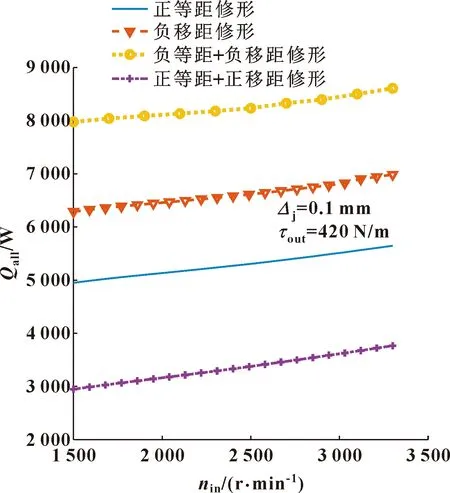
图13 转速变化对不同修形方式下整个啮合过程中总的摩擦损失功率的影响Fig.13 Effect of the various input speeds on the total rollingpower loss for the different modification schemes

4 结论

基于Ostwald模型建立摆线针线接触润滑数值模型，研究4种摆线轮修形方法对啮合传动过程中摩擦润滑状态的影响规律。得到以下结论：

(1)修形量一定的情况下，正等距+正移距组合修形得到的啮合过程中最小油膜厚度最大，摩擦因数、摩擦损失功率以及总的摩擦损失功率最小，摩擦润滑接触状态最优；而负等距+负移距修形得到的啮合过程中最小油膜厚度最小，摩擦因数、摩擦损失功率以及总的摩擦损失功率最大，摩擦润滑接触状态最差；正等距单修形摩擦润滑接触状态优于负移距单修形方式。

(2)对负移距单修形与正等距+正移距组合修形方式下修形量变化对摩擦润滑状态影响进行分析，结果表明：随着修形量的增加，啮合区间减小，大部分啮合区间膜厚减小，摩擦因数略微增大，摩擦损失功率增大，整个过程总的摩擦损失功率增加，摩擦润滑状态变差。

(3)随着转速增加，修形齿廓啮合过程中最小油膜厚度增大、摩擦因数减小、摩擦损失功率增大、总的摩擦损失增加。随着转速增加，不同修形方式下啮合过程中总的摩擦损失功率都线性增加。