数学教学中多向思维能力的培养

陈恩余

（湄潭县天城完小 贵州 遵义 564100）

为了全面提高学生的综合素质，增强学生适应社会发展的能力，我们需要针对学生的年龄特征和心理特点、学科背景和特点、知识面各个方面，在教学中做到有理、有据、有趣、有度，利用一切有利的因素，不失时机地对学生进行多向思维能力的培养。那么在数学教学中怎样培养学生的多向思维能力呢？我认为应引导学生从不同的角度去进行分析、观察思考、解答题目，从而扩展学生的视野和思路，才能培养学生的多向思维能力。

1.从多角度的观察、分析解答题目的过程中培养学生的多向思维能力

例如：教学应用题：“一辆汽车从甲地开往乙方，第一小时行了全程的1/4，第二小时行了全程的5/18，两小时行了114千米，甲乙两地之间的公路长多少千米？”

先引导学生分析：“第一小时”和“1小时”的区别，“第二小时”和“2小时”的区别，“114千米”是前面两小时共行的路程，所以要求甲乙两地之间的公路长得先求出两小时共行路程对应的分率，把两地的公路长看作单位“1”，得出：

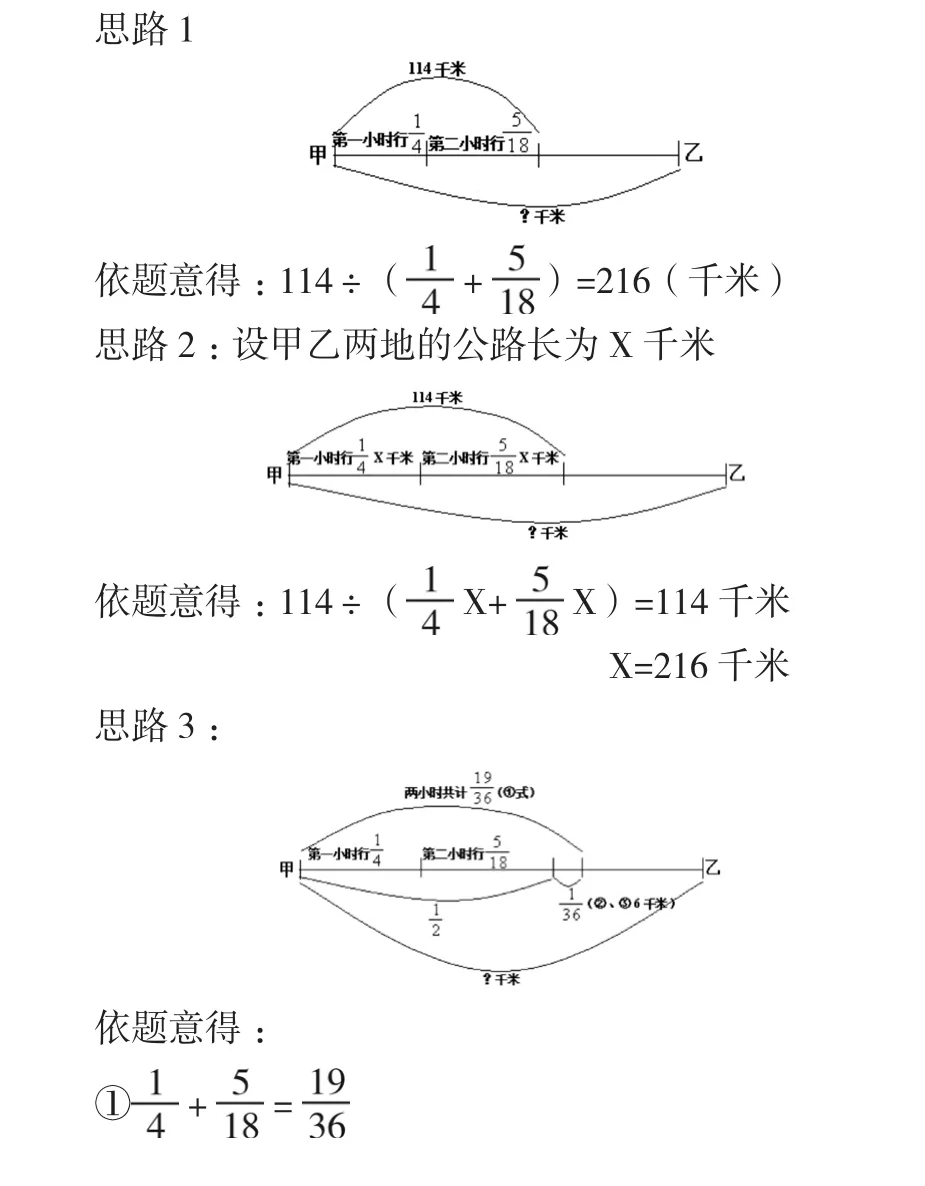
通过这样的分析解答，学生就会对同一道题目从多角度、多方面去寻找解题思路，思路1与思路2是由条件到问题的集中思维和逻辑思维，思路3与思路4是由问题到条件的逆向思维和发散思维，同时通过思路1与2对比，思路3、4对比，分析解答方法汇融与逻辑推理能力训练，培养学生的多向思维能力，从而提高学生解决问题的能力。

2.在不同的解题方法中去培养学生的多向思维能力，又如在教学“某印刷厂的男工与女工的人数比为4:3，全厂有职工364人，男女职工各有多少人？”一题时，先让学生独立思考，用不同的方法解答，得出：

思路4：用归一法解答（总人数看作单位“1”）

4+3=7

364÷7=52

男工为：52×4=208（人）

女工为：52×3=156（人）

思路5：依据男工与女工的人数比例出方程解答：

设男工人数为X人，则女工人数为（364－X）人，依题意得：

X：（364－X）=4：3

X=208

女工为：364－208=156（人）

思路6：设男工与女工的比例系数为X，那么男工为4X人，女工为3X人，依题意得：

4X+3X=364

X=52

男工为52×4=208（人）

女工为52×3=156（人）

通过上列的多项解题思路可知，解题思路多种多样，培养学生的思维方法是多方面的，可以从整体入手解答（思路1），培养学生的发散思维能力。可从问题入手解答（思路2、3、4），培养学生的逆向思维能力和发散思维能力，可从解答题目内部蕴涵的隐含条件入手去解答（思路5、6），培养学生的抽象思维能力。从条件到问题的分析解答过程中去培养学生的逻辑思维能力和发散思维能力，从一题多解的解题方法（思路1、2、3、4、5、6）中去培养学生的数学思考能力和解决实际问题的技能，让学生获得解决问题的基本活动经验，提高学生的多向思维能力。

3.从图形与几何的构建中培养学生的多向思维能力

如在解答“已知，如图，ABCD是长方形，宽BC=4cm，求阴影部分的面积”一题时，让学生从长方形到阴影部分中的圆，循序渐进仔细观察，从表象上看是求阴影部分的面积。重点则是弄清阴影部分与整个图形在空间形式上的组图关系，难点则是求阴影部分中小圆的半径，辅导学生从外到内分析发现，阴影部分面积是长方形面积减去以A、B两点为圆心的两个1/4圆面积，再减去阴影部分中小圆的面积（难点），从构图上看，宽为⊙A（或⊙B）的半径（4cm），长为半径的两倍（2×4cm），因此长方形中两个1/4圆面积易求出，再向阴影部分里看小圆与整个空间图形的构图关系（此时思维进入难点），小圆与⊙A、⊙B是两两外切，再与长CD相切，找出小圆圆心O将⊙O半径看作r，连接OB必过切点，OB长（4+r）cm，再连接OE，OE长为（4－r）cm，这种由点到线再到面的构建是培养学生空间想象能力和抽象思维能力的捷径，在建立Rt△OEB后，根据勾、股、弦三边关系得到

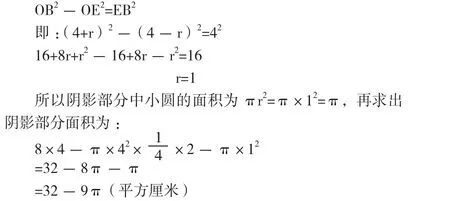
在解答过程中，涉及到的概念很多：①长方形面积，②圆的概念及面积计算，③Rt△OEB的构建及勾股弦三边关系，④两数和平方，⑤两数差平方，⑥方程概念及列解方程，既涉及空间与图形部分，又涉及数与代数部分，知识面广泛，涵盖了四到八年级的概念，所以学生理解起来跨度、难度很大。

这种由数量关系到图形面积的计算就是抽象思维和逻辑思维的培养过程，从而突出数学是研究“数量关系和空间形式的科学”主旨，从长方形面积减去两个1/4圆面积再减去阴影部分中小圆面积，这种由外到内的思维递进关系既培养了学生缜密的思维技巧，又拓展了孩子的思维空间。从A、B两点认识，⊙A、⊙B的1/4圆面联想到⊙O。既复习了有关圆的半径、切线等相关知识，又培养了用点线面建立空间图形及勾、股、弦，再求⊙O。半径r这种解决问题的基本活动经验，又培养了学生的数学思考能力。

像这样由已知条件进入题目分析→构建Rt△OEB三角形空间相象→再求出⊙O半径r→求出⊙O面积→再求出阴影部分面积的这种由条件到问题解决的思维过程就是培养学生集中思维和逻辑思维的过程中，使学生学习轻松，积极主动，有收获学习成功的获得感。激发了学生的学习热情，因势利导，让学生进入学习的主体角色，学习主线贯穿学习过程。既体现教师是组织者、参与者、引导者、合作者，又培养了学生热爱本学科的情感态度，培养了学生的多向思维能力，学生获得了解决实际问题的活动经验。

通过以上例题的学习可知，培养学生的多向思维能力，单靠学习书本上的题目是不够的，只会书中例题的单一解法是很肤浅、贫乏的，必须深刻理解数学知识的内涵，发挥组织者、参与者、引导者、合作者的作用，培养学生的数学思维能力与热爱数学知识的情感态度，才能提高学生解决实际问题的技能。同时要解放儿童的头、手、口，解放儿童的时间和空间，学习目标明确，在学习主线中彰显学生的主体地位，担责育人，有难不避，尽力所能，心爱全体学生，让学生既有“点线面体勾勒空间轮廓大千世界的遐想，又有加、减、乘、除演绎数学世界无限苍穹”的技能，引导学生多方面分析问题，丰富、充实自己的头脑，多角度、多方位思考解答，提高解题技能，才能提高学生的多向思维能力。