Implicit Finite Difference Scheme for Singularly Perturbed Burger-Huxley Equations

KABETO Masho Jimaand DURESSA Gemechis File

Department of Mathematics,College of Natural Sciences,Jimma University,Jimma,Ethiopia.

Abstract. In this paper, an implicit finite difference scheme is presented to solve one dimensional unsteady singularly perturbed Burger-Huxley equation. The quadratically convergent quasilinearization technique is used to linearize the nonlinear term of the equation. The innovative significance of this paper is the procedure to consider initial guesses in order to start the quasilinearization technique. This basic initial guessing causes to produce a more accurate solutions with the small iteration number for the problem under consideration. The derivatives are replaced by finite difference approximation, then we obtain the two-level time direction and the three-term recurrence relation in the spatial direction. The convergence analysis of the proposed method has been established. Numerical experiments were conducted to support the theoretical results. Further, the result shows that the proposed method gives a more accurate solution with a higher rate of convergence than some existing methods.

AMS Subject Classifications: 65M06,65M12,65M15

Key Words: Singularly perturbed;Burger-Huxley equation;higher-order;accurate solution.*Corresponding author.Email addresses:maashookoo.reemii@gmail.com(M.J.Kabeto),gammeef@gmail.com(G.F.Duressa)

1 Introduction

Consider one-dimensional unsteady singularly perturbed Burger-Huxley equation of the form:

where 0<ε ≪1 is a perturbation parameter. The solution domainD=(0,1)×(0,T],andα≥1,β≥0,γ∈(0,1)are given constants. Such equation describes the interaction between convection, diffusion and reaction processes [1]. Burger-Huxley equation describes numerous fascinating phenomena such as busting oscillation[2],interspike[3],population genetics[4],bifurcation and chaos[5].In the former few decades,several analytical methods were suggested to solve the Burger-Huxley equation. For example,by using Hirota method,Satsuma[6]obtained an exact solitary solution for this equation.Wang and other researchers in[7]built an exact solitary wave solution of the generalized Burger-Huxley equation. In [8], Wazwaz constructed some travelling wave solutions for the generalized forms of Burgers,Burgers-KdV and Burger-Huxley equation by using the standard tanh-function technique. The most innovative and robust numerical methods have been conducted on several families of singularly perturbed parabolic problems like in,[9–13].

Recently,several researches give attention to solve Burger-Huxley equation by the numerical methods such as different classes of domian decomposition method[14–17],variational iteration method[18],finite difference scheme[19,20],different kinds of spectral methods[21,22], family of collocation method[23,24], computational meshless method[25]. However, the nature of the solution of singularly perturbed Burger-Huxley problem exhibits boundary layer.Because of the occurrence of this layer,the above mentioned methods are in question and known to be insufficient to estimate the accurate solution.

Consequently,to obtain uniformly convergent method,Kaushik and Sharma[26]establishes on nonuniform mesh for solving Eq. (1.1). Gupta and Kadalbajoo [27] assembled a numerical scheme that contains of implicit-Euler method which is first order uniformly accurate to discretize in temporal direction on a uniform mesh and a monotone hybrid finite difference operator to discretize the spatial direction with a piecewise uniform Shishkin mesh.

Research has been conducted to improve on the performance of Shishkin meshes while recalling some of their simplicity.The use of a piecewise uniform mesh with choosing transition parameter. The extendibility of the methods using meshes of Shishkin type to higher dimensional problem clarifies why people are interested in using them. Another advantage of Shishkin meshes over other types of meshes,is the convenience to handle complicated higher-order methods. Thus, in this paper, we aim at formulating higherorder fitted mesh of Shishkin type to solve the singularly perturbed Burger-Huxley equations.

Evidently,the methods obtainable in[26,27]are of the layer-adapted mesh approach.Moreover,recently Liu,Li-Bin,and others in[1]constructed a robust adaptive grid method for the problem(1.1).However,the obtained accuracy of the solution needs improvement which indicates that still for such kind of problems requests to develop another numerical method to produce a more accurate numerical solution. To serve this purpose, we will devise more accurate, stable, and consistent scheme for the problem under consideration. We first linearized the nonlinear terms by using quasi-lineariztion technique. Then,the average finite difference approximation is applied to approximate the derivatives of the differential equation. The convergence analysis is given to show that the presented method is second-order convergent.

2 Properties of Continuous Solution

In this section, a priori estimate for the solution of Eq. (1.1) on the solution domain denoted byD. Suppose the base boundary Γb={(x,t):t=0,x∈[0,1]},left boundary Γl={(x,t):x=0,t∈[0,T]}and right boundary Γr={(x,t):x=1,t∈[0,T]},then∂D=Γl∪Γb∪Γr.For any given functiong(x,t)∈C0,the maximum norm is defnied as follows

Lemma 2.1.(Maximum Principle): Let v(x,t)∈C2,1( ¯D),be a smooth function such that Lx,εv(x,t)≥0,where ∀(x,t)∈D and v(x,t)≥0on ∂D. Then,v(x,t)≥0,∀(x,t)∈D.

Proof.The proof of this Lemma is done on[27].

A direct importance of this maximum principle is to establish the following stability estimte.

Lemma 2.2.Let u(x,t)be the solution of problem(1.1),then we have,

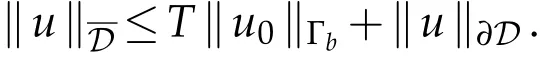
To drive the convergence and stability of the time direction, we give the bounds on the time derivatives as follows:

Lemma 2.3.Let u(x,t)be the solution of problem(1.1),then there exists a constant C,independent of ε,such that

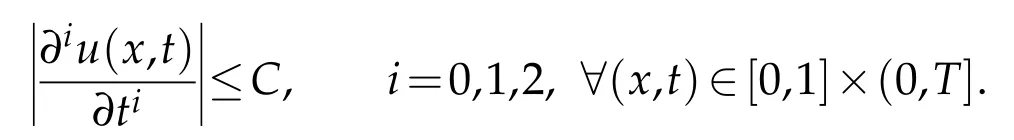
Proof.It follows from lemma (2.2), we can obtain. Next one can obtain the first-order derivative bound with respect to time variable as follows. Differentiating the initial funtion concerning to the space vatiable as∂u(x,0)/∂x=u′0(x)and∂2u(x,0)/∂x2=u′′0(x),which yields

On the boundariesx=0 andx=1,we obtain∂u(x,0)/∂t=s′0(t),∂u(1,t)/∂t=s′1(t),t∈(0,T].Therefore,for sufficiently smooth functionsu0(x),S0(t)andS1(t),there exists a constantC1,such that

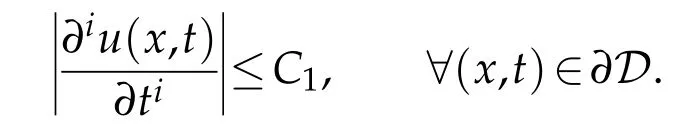
For∀(x,t)∈(0,1)×(0,T],it follows from Eq. (1.1)that

As the operatorLx,εis uniformly stable,using lemma(2.2),we get

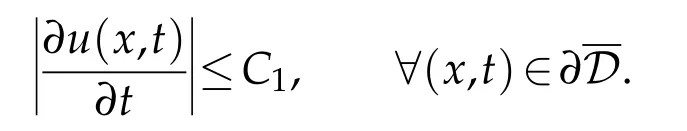
Similarly,we get the bound for the second-order derivative∂2u(x,t)/∂t2.

3 Formulation of the Numerical method

Consider Eq. (1.1),which re-written as

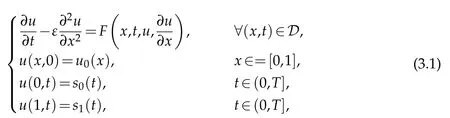
where

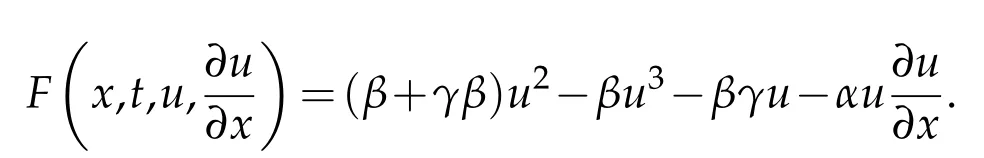
Let us consider the homogenous part of Eq. (3.1)written as

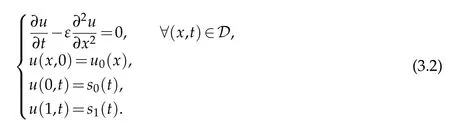
We look for a solution to the dimensionless heat equation of the form of Eq. (3.2), forε=1,using the concept of separation of variables,we get the solution of Eq. (3.2)as

which satisfies both the initial and boundary conditions.

To linearize Eq.(3.1), by applying the quasilinearization technique on the nonlinear term,for reasonable initial guess of the form of Eq. (3.3)is given by

Thus,the nonlinear termF(x,t,u,∂u/∂x)can be linearized initially as;

Substituting Eq. (3.5)into Eq. (3.1)and inducing for iteration numberi=0,1,...,we obtain the linearized differential equation.

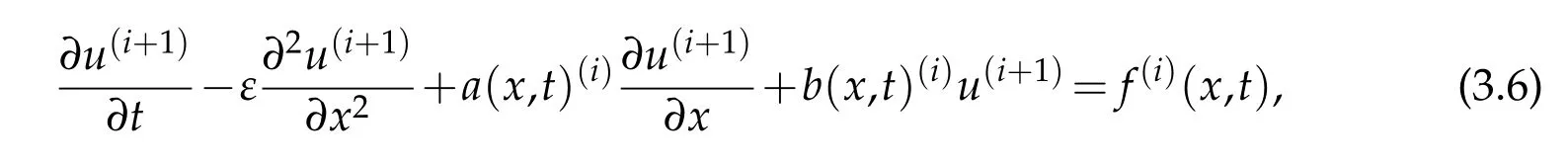
where

LetMandNbe positive integers,then discretize the interval of[0,1]and[0,T]intoMandNequal sub-intervals of the spatial and temporal direction respectively with uniform step lengthhandk. Thus,the gird points(xm,tn)can be generated by:

At the fixed(i+1)−thiteration,let us re-write equation(3.6)at the nodal pointas:

Then , to get the fniite difference approximation for, we considered the Taylor’s series expansion:

Subtracting Eq. (3.10)from Eq. (3.9),gives the second-order finite difference approximation:

where the truncation term

Considering the remaining terms of Eq. (3.8),at the average ofnthand(n+1)thtime level,we have:

where for the truncation term

Substituting Eqs. (3.11)and(3.12)into Eq. (3.8),and then re-written as the three-term recurrence relation in terms of the spatial direction and two-term recurrence relation in terms of the temporal direction as:

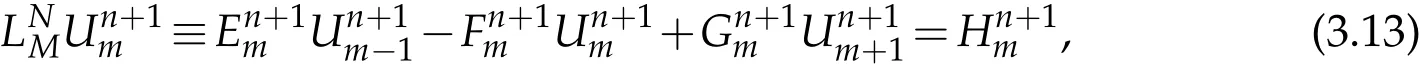
where

Note that,in this paper,we solve the problem under consideration numerically using Eq.(3.13)at the first iteration.

4 Convergence analysis

In this section,we carry out the stability analysis and derive the truncation error for the formulated scheme,and then we estimate its convergence.

Lemma 4.1.(Discrete Maximum Principle):Assume that the ith iteration of the discrete functionψnm satisfies ψnm ≥0on the discrete boundaryΓNM and LNMψnm ≥0,∀(xm,tn)∈DNM.Then ψnm ≥

Proof.Suppose that there exists a pointsuch thatThus,from te given conditions on the boundary ΓNM,we have,which implies that. It follows from the defniition of the pointthat

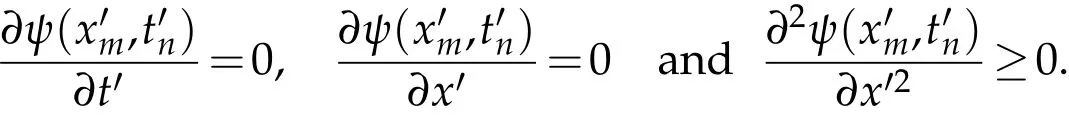
This lemma is used to prove the following uniform stability estimate.

Lemma 4.2.Uniform stability estimate for Eq.(3.7)at any time level is estimated if Unm is any function such that Un0=UnM=0,for n=0,1,2,···,N. Then

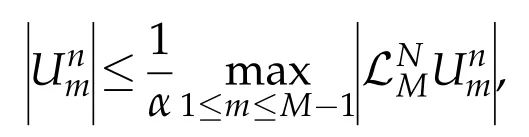
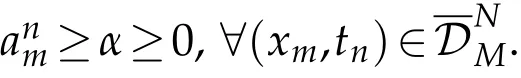
Proof.Assume thatψ±be the barrier mesh function defined by:

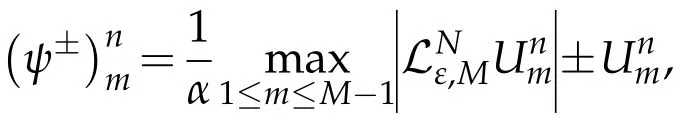
Sinceanm≥αand from Lemma(4.1),we haveLNMUnm≥0,which concludes that0,on.Hence,the required estimate.

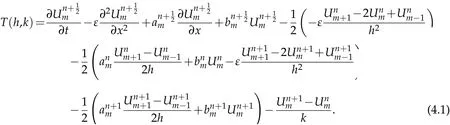
By Taylor’s series expansion,we have

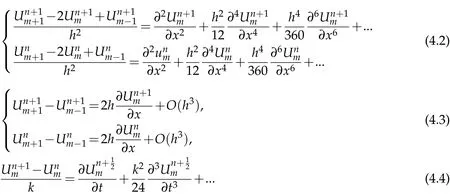
Recall that the relations for the average is given by

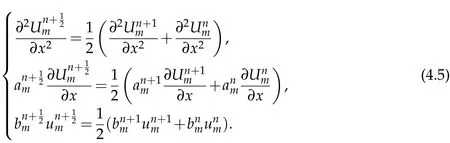
Using Eqs. (4.2)-(4.5)into Eq. (4.1),we get

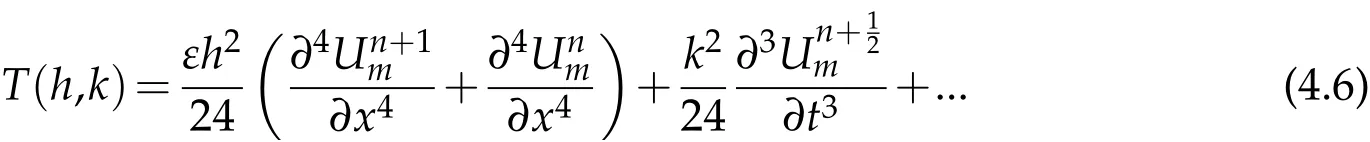
Hence,from Eq. (4.6),we have

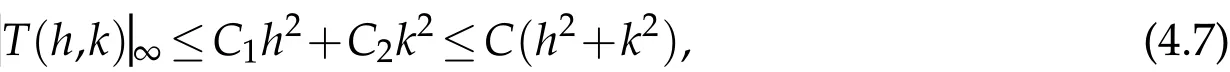
where

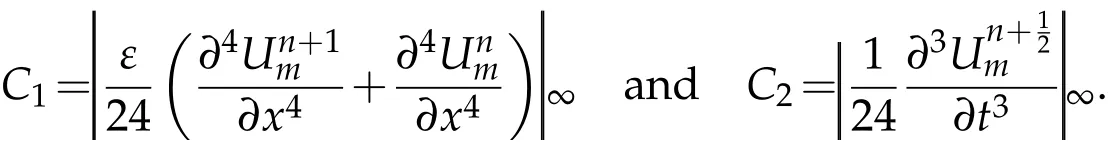
Thus,the constantCis independent of the mesh parametershandk.

5 Numerical iIllustrations and discussions

In this section,we considered model examples of singularly perturbed Burger-Huxley equations to validate our theoretical results. These examples have been chosen since they have widely discussed in the litrature under consideration. The exact solution for the considered examples are not available. Hence, the maximum absolute errors are calculated by double mesh principle,[1,28,29],given by:

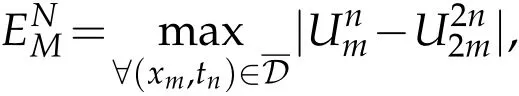
whereandare approximate solutions evaluated onandrespectively.

The corresponding rate of convergences are determined by:

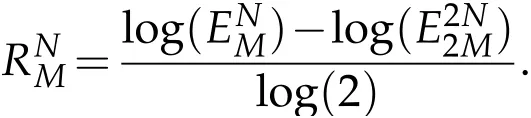
Example 5.1.Consider the following singularly perturbed Burgers-Huxley equation

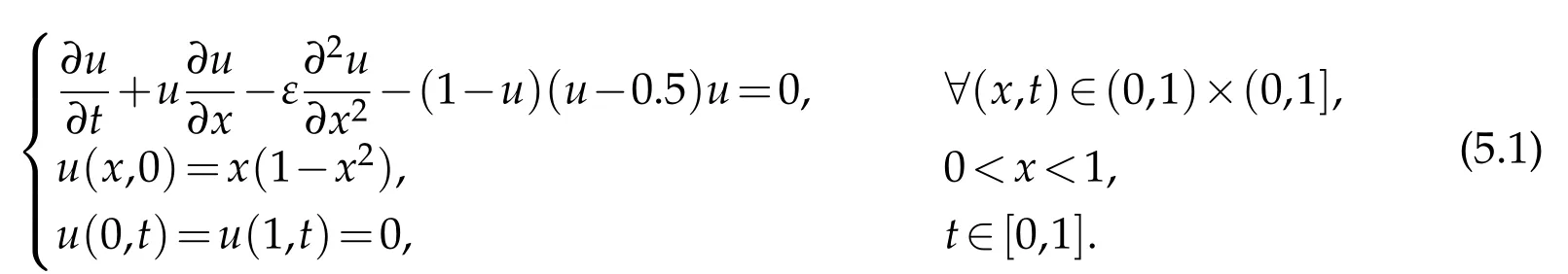
Example 5.2.Consider the following singularly perturbed Burgers’equation

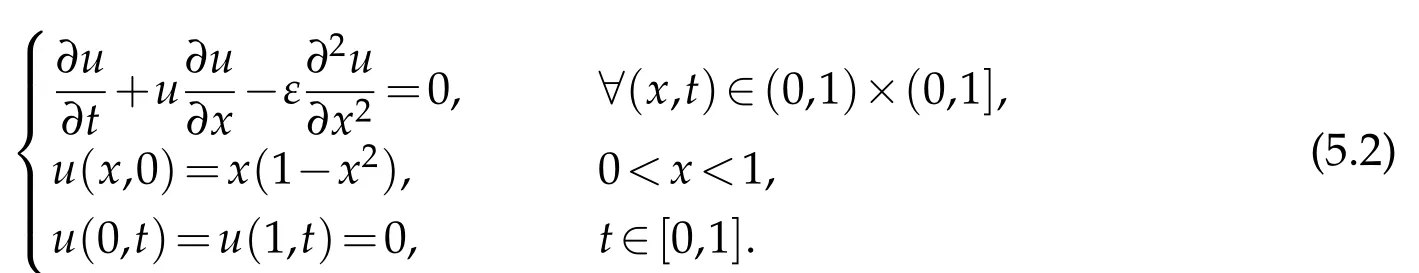
The numerical results are presented in Tables 1-4,and Figures 1 and 2.

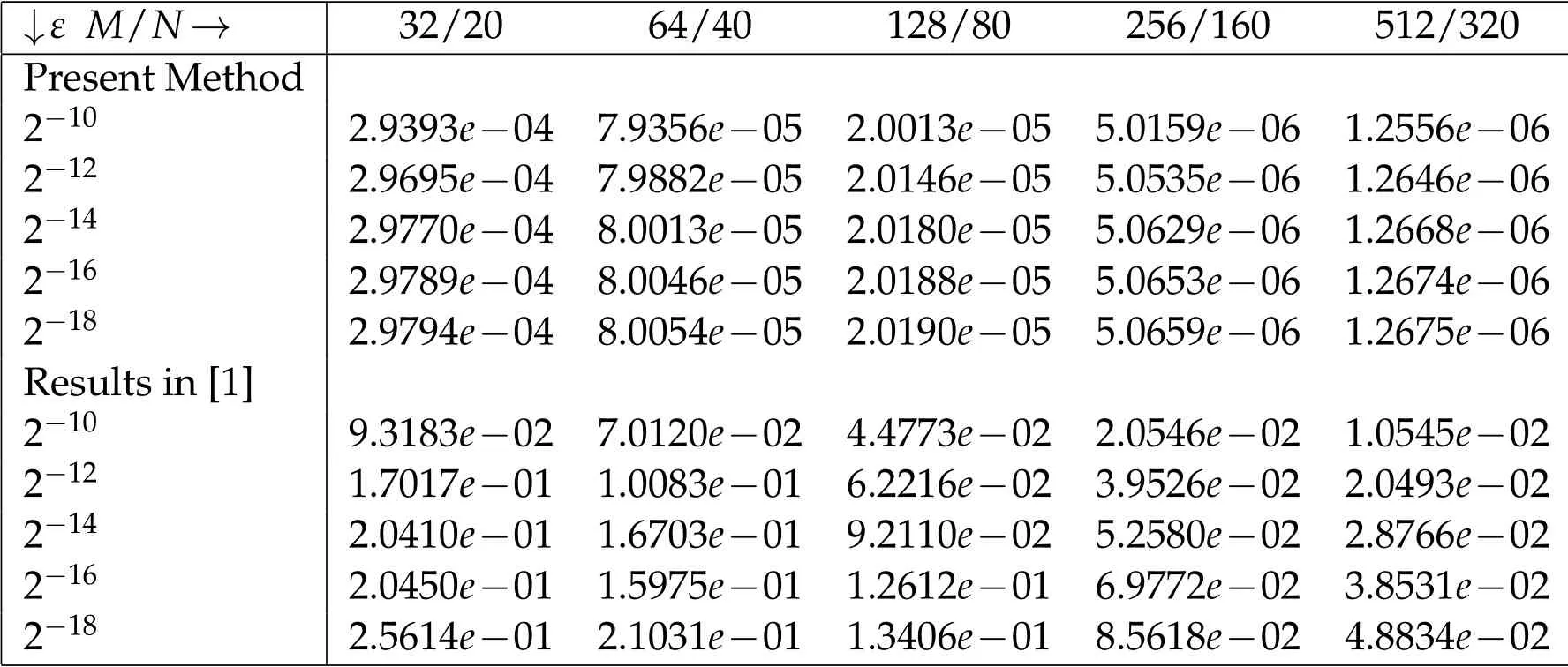
Table 1: Comparison of maximum absolute errors for Example 5.1.

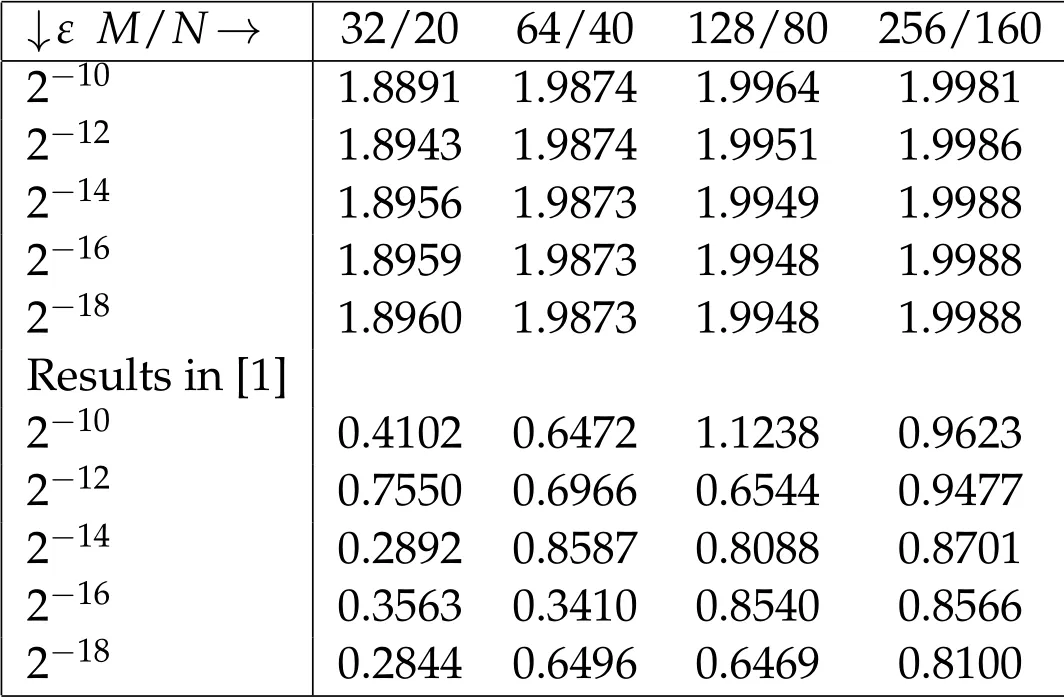
Table 2: Comparison of rate of convergence for Example 5.1.

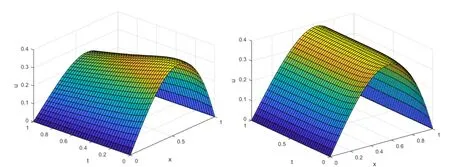
Figure 1: Solution profiles for Examples 5.1 and 5.2 respectively, when M=64,N=40,ε=2−18.

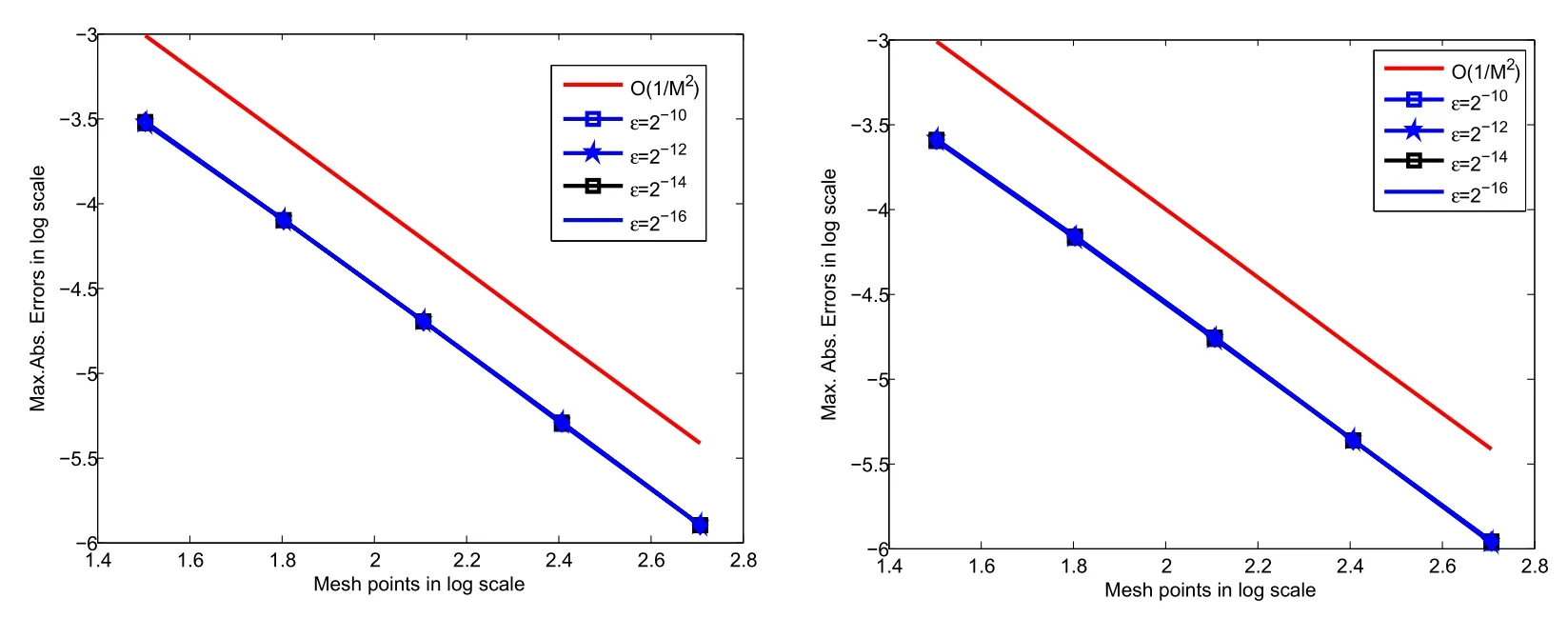
Figure 2: Log-log plots for Example 5.1 and 5.2 respectively.

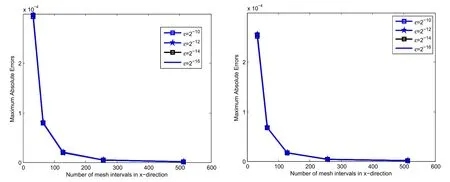
Figure 3: Maximum absolute errors via number of mesh points for Example 5.1 and 5.2 respectively.

Tables 1 and 3 shows the maximum absolute errors that demonstrates the validity of the present method, and errors are monotonically decreasing (see Figure 3) behavior with increasing the number of intervals which confirm the convergence of the method.Further, Tables 2 and 4 validates that the the rate of convergence described in Eq. (4.7).Thus,the proposed method with higher-order convergent than some existing methods in the literature.

Table 3: Comparison of maximum absolute errors for Example 5.2.

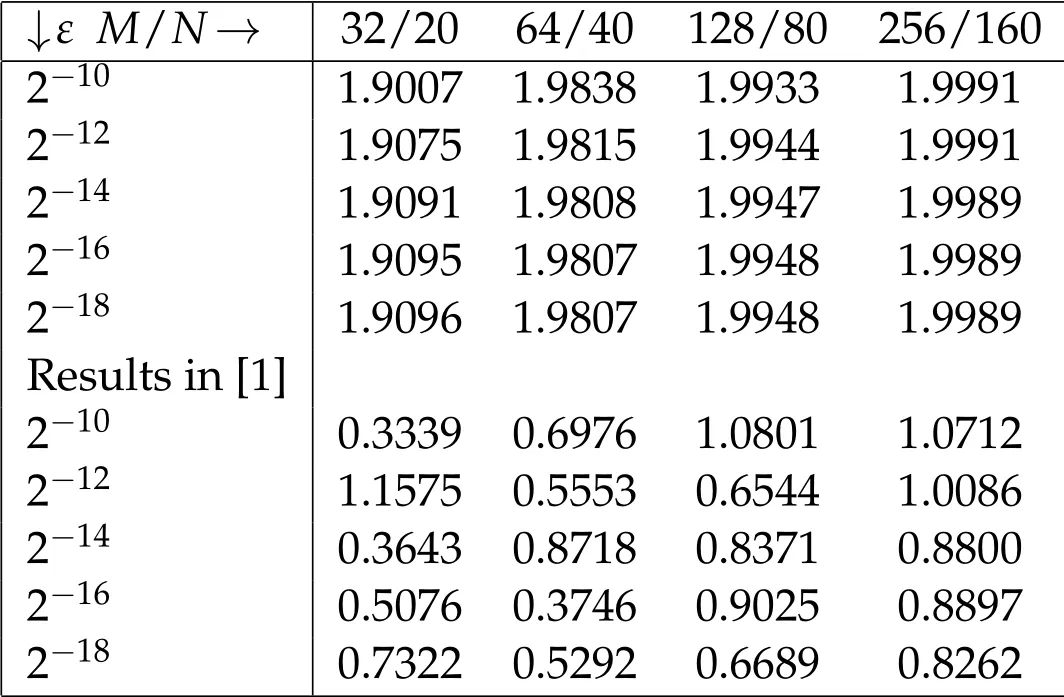
Table 4: Comparison of rate of convergence for Example 5.2.

Furthermore,the method gives more accurate solution than some existing methods in the literature. Figure 1 verifies that the physical behavior of the solutions for both Examples. Log-log plot presented in Figure 2 for the modeled examples under consideration.

6 Conclusion

In this paper, higher-order implicit finite difference scheme is presented for solving the singularly perturbed Burger-Huxley equation. At first,the nonlinear terms are linearizedby quasilinearization technique.Then,we use average finite difference approximation for the discretization of derivatives.A second-order point-wise convergent error estimations are established. It is provided that from numerical results,the proposed method gives a better accurate solution with higher order of convergence than some existing methods in the literature. Therefore, the proposed method is an implicit finite difference scheme of second-order converegnt and gives accurate solution for solving the singularly perturbed Burger-Huxley equation.

Acknowledgement

We thank Jimma University for the necessary support,reviwers and editors of the Journals of Partial Differential Equations.