An Averaging Principle for Caputo Fractional Stochastic Differential Equations with Compensated Poisson Random Measure
GUO Zhongkai,FU Hongbo and WANG Wenya
1 School of Mathematics and Statistics, South-Central University for Nationalities,Wuhan 430074,China.
2 Research Center of Nonlinear Science,College of Mathematics and Computer Science,Wuhan Textile University,Wuhan 430074,China.
3School of Artificial Intelligence,Jianghan University,Wuhan 430056,China.
Abstract. This article deals with an averaging principle for Caputo fractional stochastic differential equations with compensated Poisson random measure. The main contribution of this article is impose some new averaging conditions to deal with the averaging principle for Caputo fractional stochastic differential equations. Under these conditions,the solution to a Caputo fractional stochastic differential system can be approximated by that of a corresponding averaging equation in the sense of mean square.
AMS Subject Classifications:34C29,39A50
Key Words: Stochastic fractional differential equations; averaging principle; compensated Poisson random measure.
1 Introduction
Most systems in science and industry are perturbed by some random environmental effects, described by stochastic differential equations with (fractional) Brownian motion,L´evy process, Poisson process and etc. A series of useful theories and methods have been proposed to explore stochastic differential equations,such as invariant manifolds,averaging principle , homogenization principle. All of these theories and methods develop to extract an effective dynamics from these stochastic differential equations,which is more effective for analysis and simulation. For averaging principle, its often used to approximate dynamical systems with random fluctuations,and provides a powerful tool for simplifying nonlinear dynamical systems. The essence of averaging principle is to establish an approximation theorem that a simplified stochastic differential equation is presented to replace the original one in some senses.
The averaging principle for stochastic differential equations was first introduced by Khasminskii in paper [1], which extending the deterministic result of [2]. Since then,the theory of averaging principle for stochastic differential equations driven by different noise are considered by many authors,see[3–7].
Because the non-local property of time derivatives, the model of Caputo fractional stochastic differential equations applied in many areas, such as biology, physics and chemistry and etc.. Existence and uniqueness of solution for Caputo fractional stochastic differential have been discussed by many papers. Quite recently,some types of Caputo fractional stochastic(partial)differential equations problem are considered from the dynamic viewpoint. For example,in paper[8],existence of stable manifolds is established.In[9], the existence of global forward attracting set for stochastic lattice systems with a Caputo fractional time derivative in the weak mean-square topology is considered. The asymptotic distance between two distinct solutions under a temporally weighted norm is discussed by[10]. To the best of our knowledge,averaging principle for Captuo fractional differential equations only considered by two articles in present,see[11]and[12],it is worth noting that the average conditions given in these two papers are different,under this conditions,the corresponding averaging conclusions are drawn respectively. In this paper,we also impose a new averaging condition for our framework,which let us to derive the averaging principle for our consider problem from the theoretical derivation.
Let(Ω,F,Ft,P) be a complete stochastic base. Let(Z,B(Z)) be a measurable space andν(dz) aσ−finite measure on it. Letp=(p(t)),t∈Dp, be a stationary Ft−Poisson point process onZwith characteristic measureν. The counting measure associated withp(t) is given by, forA∈B(Z),N((0,t],A):=♯{t∈Dp:0 where∈is a small positive parameter,(dt,dz):=N(dt,dz)−dtv(dz)is the compensated Poisson martingale measures corresponding toN(dt,dz)and{Bt}t≥0is anm-dimensional standard Ft-adapted Brownian motion. We note that the above equation is a classical equation ifα=1,which has been studied by many authors.Under some conditions,which can be compared with the classic case as in[12],we derive an averaging principle for the stochastic fractional differential system(1.1). This article is organized as follows. In Section 2 we will give some assumptions and basic results for our theory. The solution of convergence in mean square between the stochastic fractional differential equations with Poisson random measure and the corresponding averaged equation are considered in Section 3. Throughout this paper,the letterCbelow will denote positive constants whose value may change in different occasions. We will write the dependence of constant on parameters explicitly if it is essential. We impose the following assumptions to guarantee the existence of the solution. H1(Lipschitz condition). There exists a bounded functionK1(t)>0 such that for allx,y∈Rd, H2(Growth condition). There exists a bounded functionK2(t)>0 such that for allx∈Rd, We also assume that theKi(t)have the same upper boundK,fori=1,2. To deal with fractional differential equation,we need the following generalization of Gronwall’s lemma for singular kernels[13,14]. Lemma 2.1.Suppose that b≥0and β>0. Assume that a(t)and u(t)are nonnegative and locally integrable functions on0≤t Then In this part, we consider the existence and uniquness for the following equation under conditions H1 and H2: Definition 2.1.A map X(t):[0,T]→L2(Ω,Rd)is called a solution of the initial value problem(2.1)if X(0)=x0and X(t)is c`adl`ag and satisfies for t∈[0,T], Using similarly methods as[15],we can derive the global existence and uniqueness of solutions for Eq.2.1. Similar problem also considered by[13]under different framework.In the following, we just given a priori estimate for the solutionX(t), which assure the existence of workspace for our problem. Theorem 2.1.Under conditions ofH1andH2, for every x0∈L2(Ω,Rd)there exists a unique solution to Eq.(2.2),such that Proof.The existence and uniqueness can be easily proved by the contraction mapping argument and hence omitted here.Next,we estimate the solutionX(t)inL∞([0,T],L2(Ω;Rd)). By employing the simple arithmetic inequality we have ForI2,by Cauchy-Schwarz inequality and the condition H2,we have where we have used the fact that{s:X(s)/=X(s−)} is countable. ForI3,by Itˆo isometry and the condition H2,we have In a similar way,forI4we have Therefore,we get for allt∈[0,T], whereE2α−1,1(·) is a two-parameter function of the Mittag-Leffler type[13]. Then we have This completes the proof of the theorem. We now study an averaging principle for a standard stochastic integral equation inRd: wherex0is a random vector satisfyE|x0|2<∞,and∈∈(0,∈0]is a positive small parameter with∈0a fixed number. To ensures an averaging principle,we need to assume the following condition. H3:There exist measurable functions:Rd→Rd,:Rd→Rd×Rmand:Rd×Z→Rdsuch that for allt>0, whereϕi(t)are positive bounded function with limt→∞ϕi(t)=0 fori=1,2,3. Remark 3.1.Note that, when we takeα=1, the above conditions are consistent with classic case. Our main result,Theorem 3.1,states that the solution of original equation(3.1)is well approximated,in the sense of mean square,by that of following equation Theorem 3.1.Assume HypothesesH1−H3. Then, for arbitrary α∈(12,1), L>0and β∈(0,2α−1),there exists a constant CL,α independent of ∈,such that that Proof.Let[0,T]be a fixed time interval. For anyt∈[0,T]we have Directly,we get ForJ1,we have Due to the Cauchy-Schwarz inequality,conditions H1 and(3.2)in H3,we get ForJ2,using the Itˆo isometry,we have By conditions H1 and(3.3)in H3,we obtain Finally,we take estimate onJ3. Using the Itˆo isometry yields and so,by H1 and(3.4)in H3,we have Therefore,from(3.7)–(3.9),Theorem 2.1,one can get where we have used the fact that{s:X∈(s)/=X∈(s−)or Z∈(s−)/=Z∈(s)}is countable. By settingandfrom Lemma 2.1,we have By selectingβ∈(0,2α−1) andL>0, such that for everywe obtain(3.6). This completes the proof. Acknowledgments Zhongkai Guo supported by NSF of China (Nos. 11526196, 11801575) and the Fundamental Research Funds for the Central Universities, South-Central University for Nationalities(Grant Number: CZY20014). Hongbo Fu is supported by NSF of China(Nos.11826209, 11301403) and Natural Science Foundation of Hubei Province (No. 2018CFB688).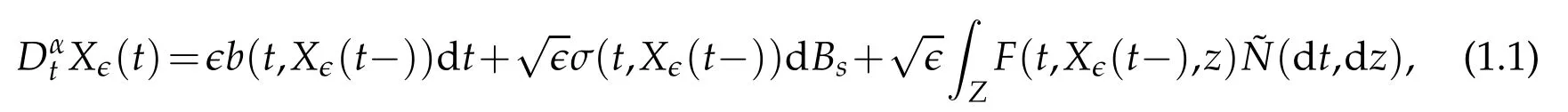
2 Stochastic differential equations with Poisson random measure
2.1 Basic Hypothesis and some useful results

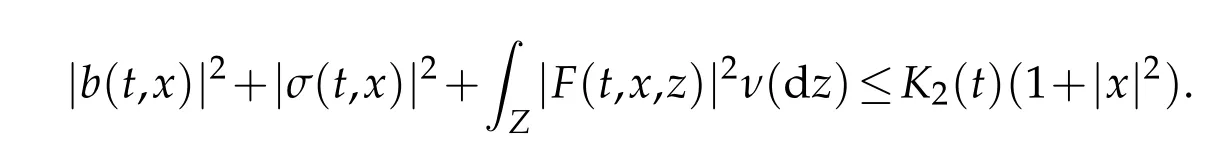

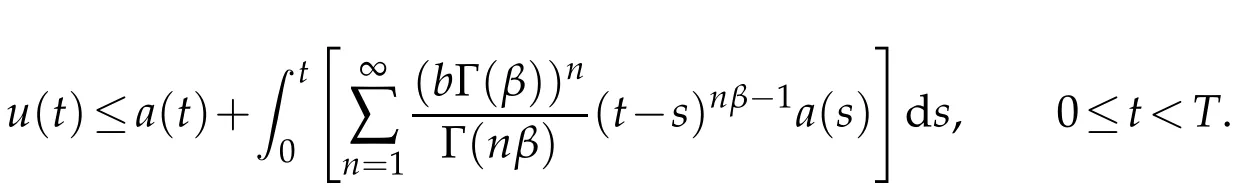
2.2 Existence and Uniqueness



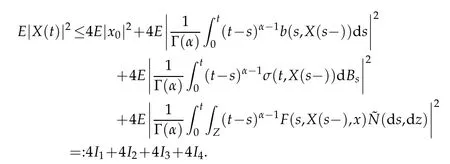
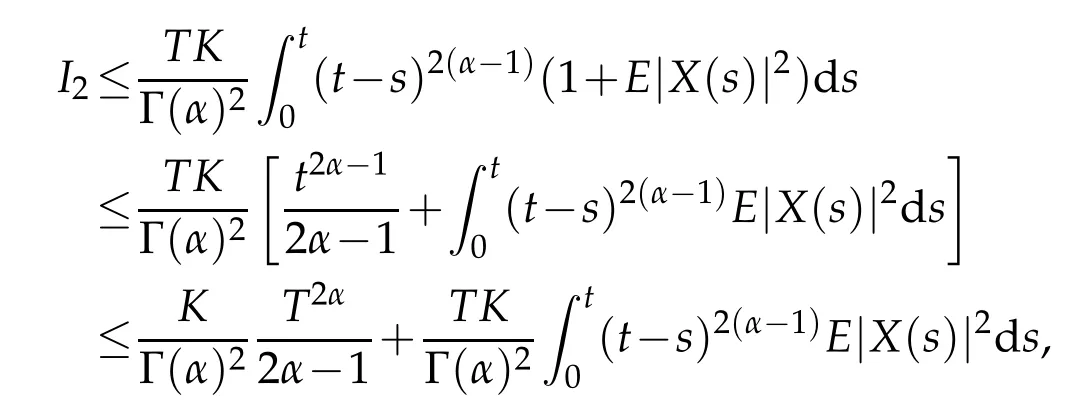
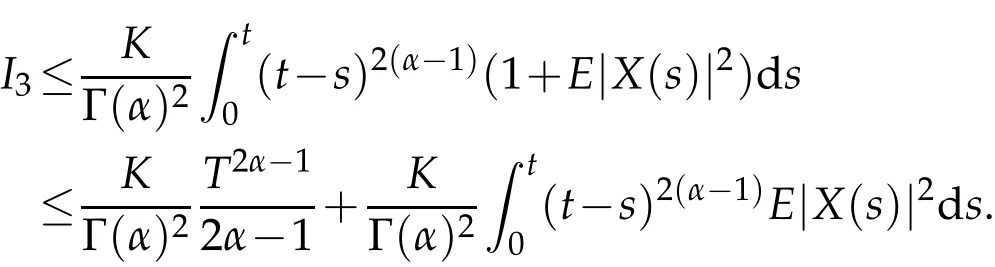
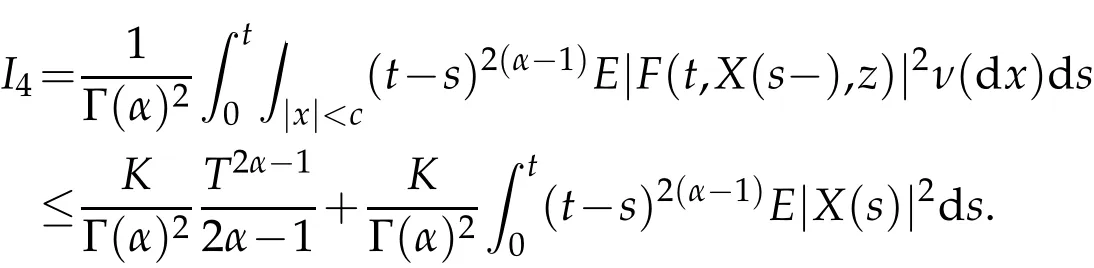

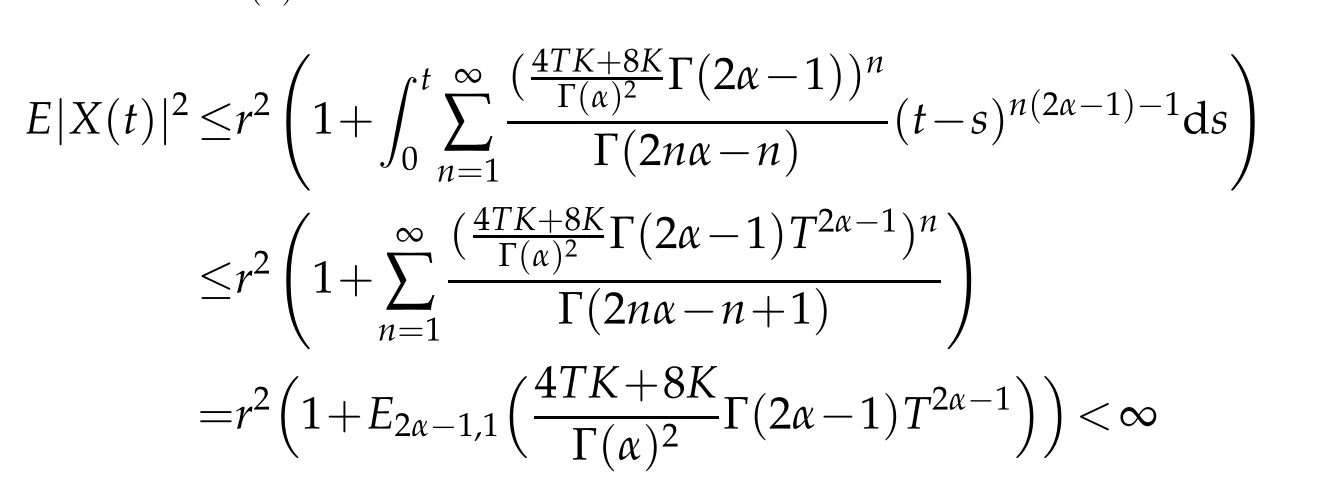
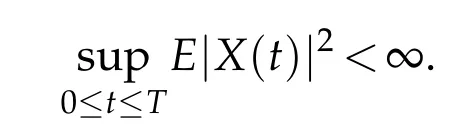
3 An averaging principle

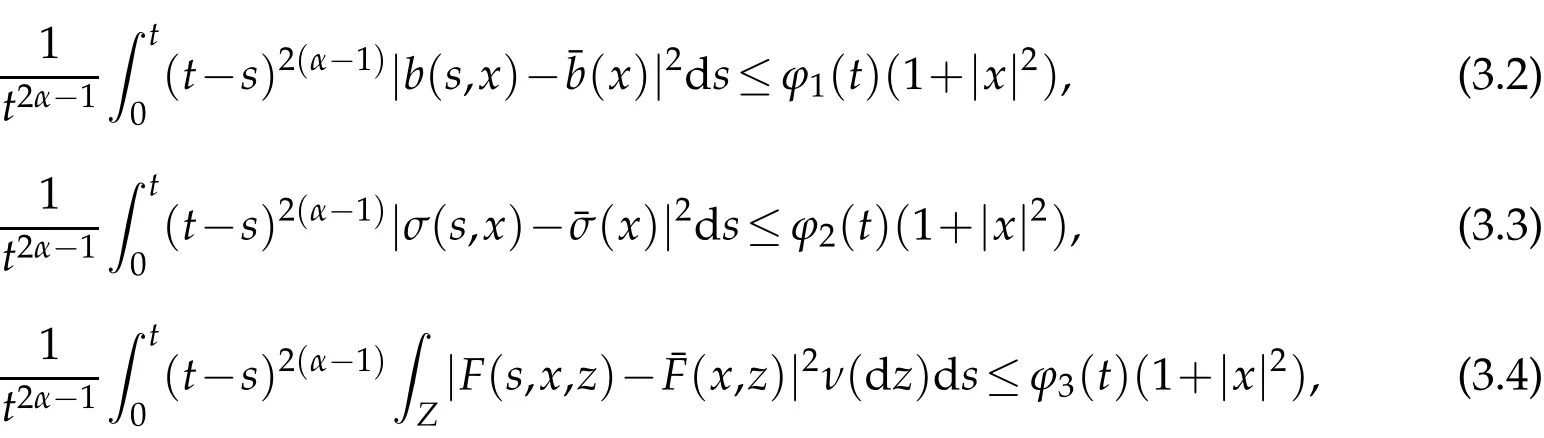
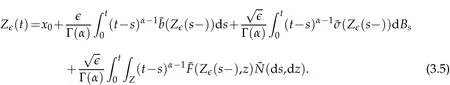
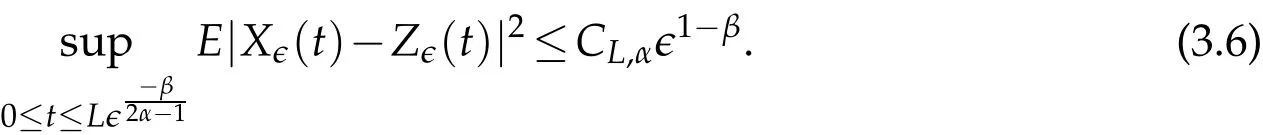









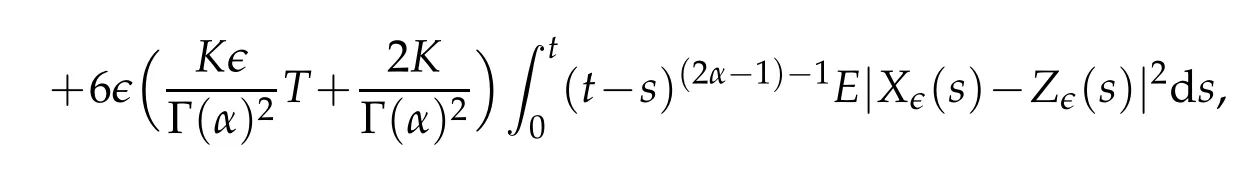
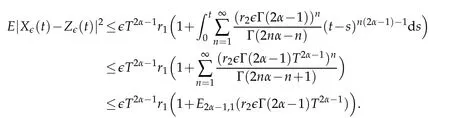
 Journal of Partial Differential Equations2022年1期
Journal of Partial Differential Equations2022年1期
