Integrated Pest Management System with Impulsive Control of Spatial Heterogeneity

ZHOU Hongling,SHEN Lin,,and WANG Shu

1 School of Mathematics and Statistics,Huanghuai University,Zhumadian 463000,China.

2 School of Mathematics,Faculty of Science,Beijing University of Technology,Ping Le Yuan 100,Beijing 100124,China.

Abstract. An impulsive integrated pest management system with diffusion is investigated within this paper. The conditions for pest eradication of the impulsive system without natural enemies are established based on the Krein-Rutman theorem and the comparison principle for parabolic equations. Integrated pest management can be achieved at an exponential rate,when the principal eigenvalues of the auxiliary system is large enough. Numerical simulations are presented to demonstrate the theoretical results. A discussion is given at the end.

AMS Subject Classifications: 65Q10,68Q85,68U20

Key Words: Integrated pest management;eigenvalue problem;pest control;diffusion.*Corresponding author. Email addresses: 8210s@163.com(H.L.Zhou),8810s@163.com(L.Shen),wangshu@bjut.edu.cn(S.Wang)

1 Introduction

The concept of integrated pest management(IPM)was introduced in the late 1950s and was widely practised during the 1970s and 1980s [1–4]. It is defined as a process consisting of the balanced use of all the pest controls that are environmentally compatible,economically feasible,and socially acceptable to reduce pest populations to tolerable levels. And pest control often involves biological,cultural,and chemical control[1–6].

Biological control,which is defined as the suppression or the elimination of pest populations by natural enemies,has been an important aspect in an IPM strategy[6].Natural enemies used for biological control can be divided into three categories: Predatory enemies, including lacewings, ladybugs and many insectivorous birds; Parasitic enemies,including parasitic wasps, parasitic flies, etc; The pathogenic microorganism, including the bacterium,bacillus thuringiensis,and so on. This control strategy is usually used by releasing natural enemies at a critical time to reduce a pest’s population[5,7,8]. Biological control has been applied to greenhouse culture,the use of Encarsia formosa against Trialeurodes vaporariorum on tomatoes and cucumbers is one of the first successful cases of biological control in greenhouses[3,4,9]. Another important method for pest control is chemical control. In most cropping systems, pesticide are still the principal means of controlling pests. They can be cheap and are easy to apply, act fast [5], but chemical control also has certain harmfulness,pesticide can not only environmental pollution,but also cause plant phytotoxicity and waste of resources,and if incorrectly used,also easily lead to human and animal poisoning.

In mid 80s, there has been renewed interest in modelling IPM.Many IPM strategies such as releases of natural enemies at critical times and killing pests instantly by spraying pesticides have been proposed by mathematical models [6–16]. In [7], Liang et al.developed two novel pest-natural enemy interaction models incorporating the evolution of pesticide resistance, they investigated the number of natural enemies to be released when threshold conditions for the extinction of the pest population in two different control tactics are reached. In [16], Tang et al. modelled IPM including residual effects of pesticides in terms of fixed pulse-type actions.

However,the aforementioned above studies ignore the effect of space. The questions that arise are: in the case of uneven distribution of space,if we aim to eradicate the pest,how do we release the natural enemies? what proportion do we need to kill the pests by pesticide? To address these questions, we present an impulsive differential equation with diffusion. In the established model,(a)insect and natural enemies are all dealt with control in space; (b) distributed control of pest are considered by a combination of the action of natural enemies and impulsive control which include pesticide spraying and natural enemies releasing;(c)because of the pesticide’s impact on the natural enemies,a proportion of the natural enemies could be killed at the time the pesticide is sprayed to kill the pests[17–19]. When we ignore the effect of space, the established model can be found in many domain of the applied sciences[20–22].

The aim of this work is to determine the conditions for pest eradication by pesticide spray-ing at critical times and the role of natural enemies releasing in enhancing the control. In order to show the conditions of pest extinction, Firstly, we discuss the model without natural enemies and get the sufficient and necessary conditions of pest extinction. Secondly we analyze the model without pest and we find the positive periodic solution of natural enemies. By using the conclusion of Section 3 and Section 4,we finally get the conditions for the extinction of the pests. Examples and numerical simulations are presented in Section 6 to illustrate the feasibility of our results. Section 7 involves some concluding remarks and discussions.

2 Two Species Model

The densities of pests and natural enemies are denoted byu(x,t)andv(x,t),respectively.The habitat is denoted by Ω.uandvare described by the following dynamical model:

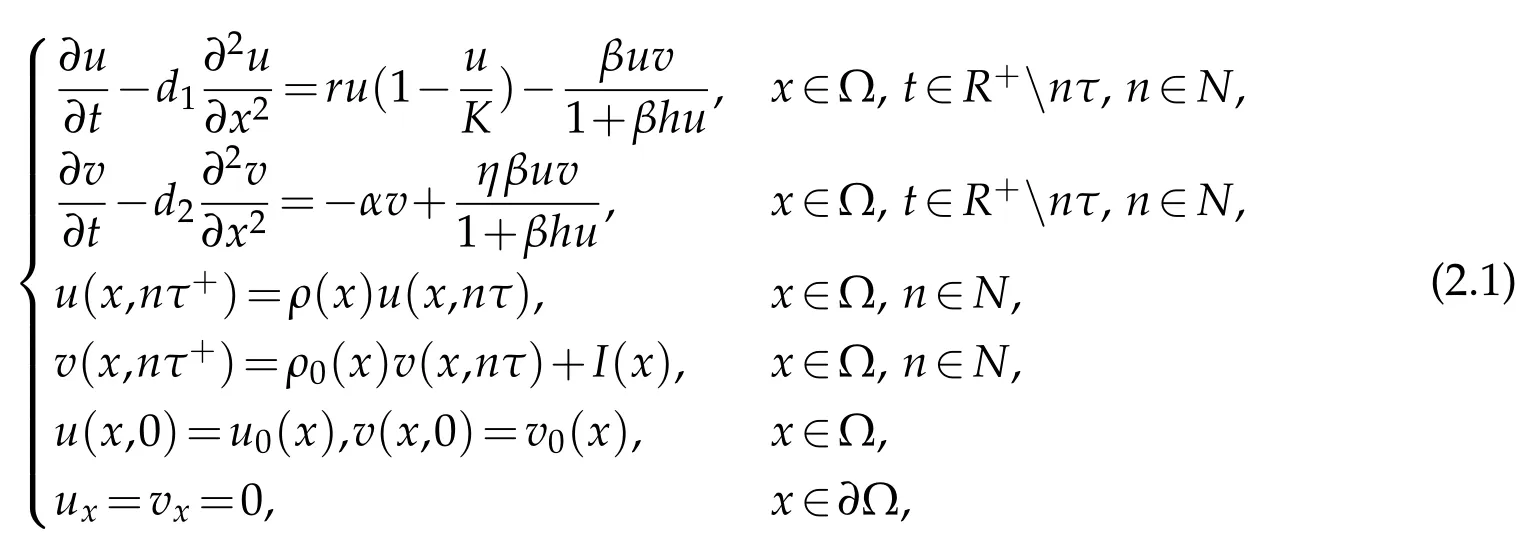
whered1,d2denote diffusion rate of pests and natural enemies,respectively;rrepresents growth rate of pests;αis mortality rate of natural enemies;Kis carrying capacity of pests;βis encounter rate;hrepresents handing time;ηdenotes conversion rate;τis the period of the integrated control.

Letu0(x),v0(x) denote the initial density of pest population and natural enemies,respectively. The Neumann boundary condition holds for the two populations. At every period,pesticide is used to control pest population,the effectiveness of pesticides is different at different locations,and the pesticide will also affect natural enemies.ρ(x),ρ0(x)denote the survival rate of the pest and natural enemies after thenth pesticide, respectively.I(x) represents the release function of the natural enemies atnτ. We assumeu(x,nτ+),v(x,nτ+)are the density of pests and natural enemies at the beginning of the(n+1)th period,u(x,nτ),v(x,nτ)are the density of pests and natural enemies at the end of thenth period. So, the pests and natural enemies at the beginning of the new period are denoted as follow

Before the research start,the following hypotheses are postulated:(H1)Ω⊂Ris a bounded domain of lengthland

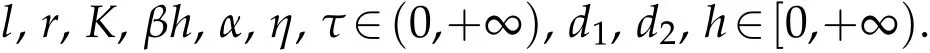
(H2)ρ,ρ0,I,u0,v0∈L∞(Ω),

wherec,c0,ρ*0∈(0,1),Imin,Imax∈(0,+∞).

We mention that the permanence and the existence of the unique periodic solution to(2.1)without the release function of the natural enemies are derived as in[23]. Please prepare your tex file. Thank you for your cooperation.

3 Single species pest model

The model without natural enemies population, but with a pesticide at the end of the period is represented as

In order to give a necessary condition and sufficient condition for the eradication of populationu. we need some basic properties of the following subsystems:

The next Lemma states the existence of the principal eigenvalue and properties related to the eigenvalue problems(see[24]).

Lemma 3.1.(i)System(3.2)exists a principal eigenvalue λ1,which is also the principal eigenvalue to the adjoined system(3.3);

(ii)there exist eigenvectors ϕ1to(3.2)andΨ1to(3.3),corresponding to λ1and satisfying

Without loss of generality, we also represent the extension by T-periodicity of ϕ1andΨ1by ϕ1andΨ1,respectively.

Theorem 3.1.Suppose u0satisfies condition(H2),(i)if the solution of(3.1)satisfiesthen λ1≥0.

Proof.(i)Assumeλ1<0. Then,for any 0<ε<−λ1,there existsN(ε)∈Nsuch that

in Ω×(nτ,(n+1)τ), and for anyn ∈N,n ≥N(ε). Thanks to the comparison result for parabolic equations[25],for anyn≥N(ε),we deduce

in Ω×(nτ,(n+1)τ),and for anyn∈N,n≥N(ε),whereis the solution to

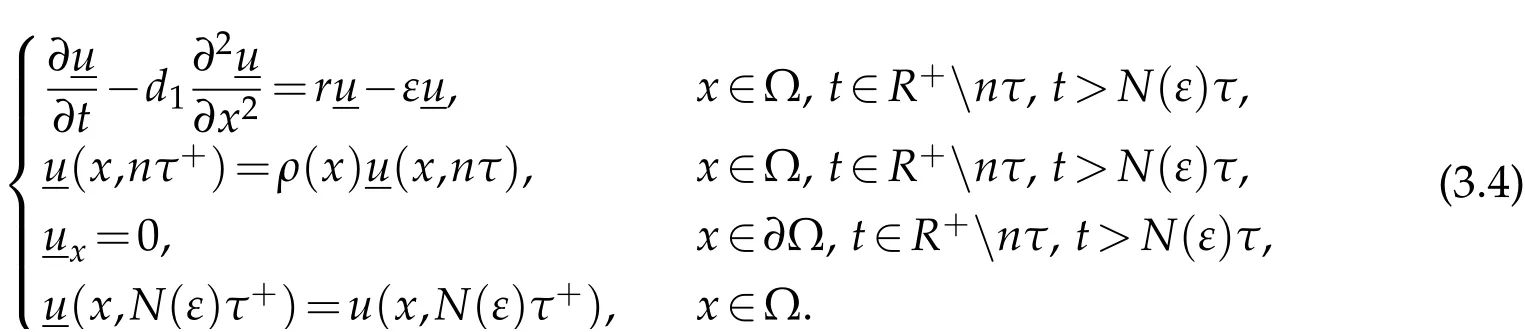
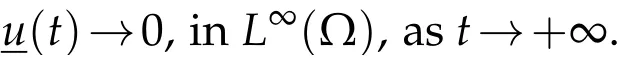
Multiply the first equation in(3.4)by Ψ1,integrate over Ω×(nτ,(n+1)τ),and recall(3.3)to discover

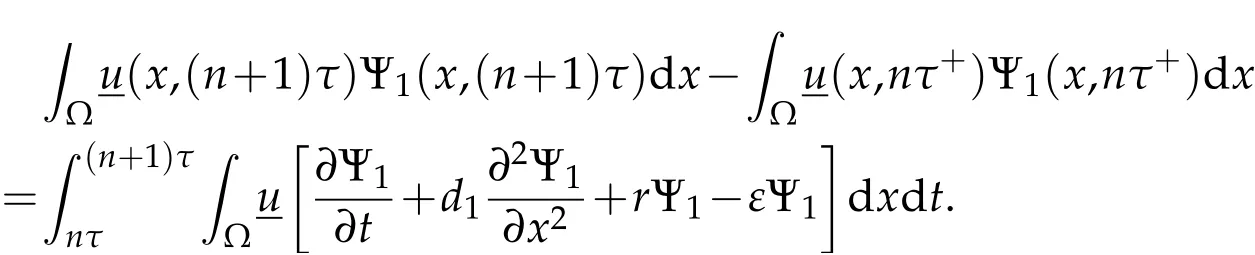
According to(3.3)and(3.4),we deduce

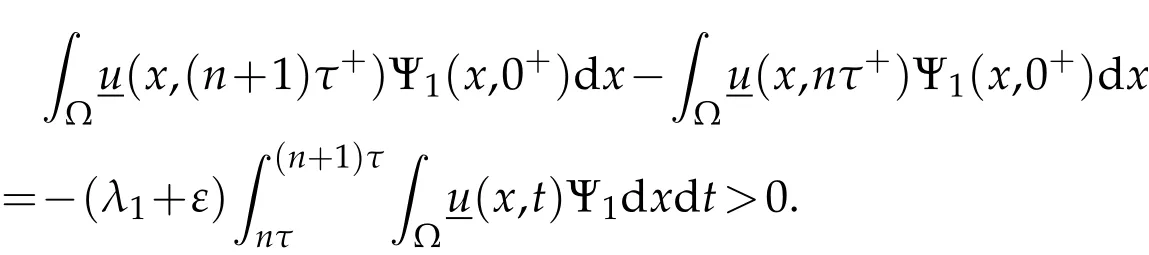
(ii)Assumeλ1>0. Thanks to the comparison result for parabolic equations[25,26],we have

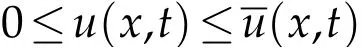
in Ω×[0,+∞),whereis the solution to

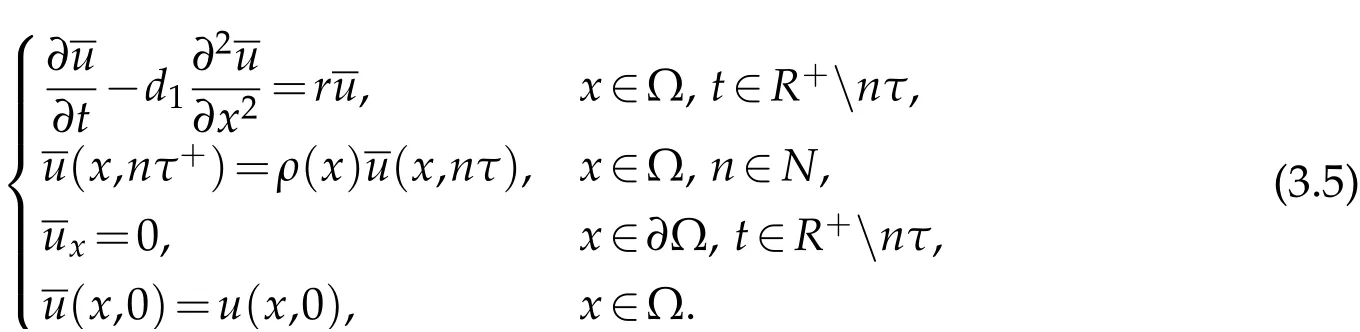
Multiply the first equation in (3.5) by Ψ1and integrate over Ω×(nτ,(n+1)τ), we deduce that

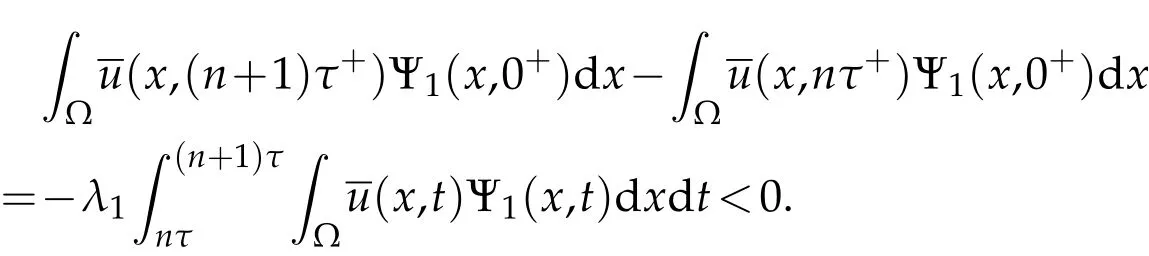
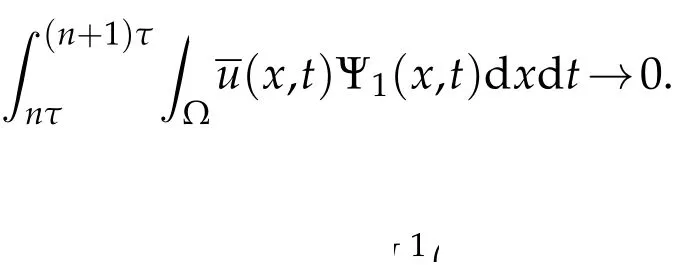
Thus,

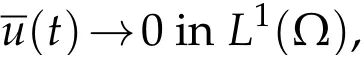
ast→+∞.The rate of convergence is that ofe−λ1t.

Sinceuis the solution to(3.5),we conclude thatast→+∞,and so,the same conclusion follows foru.

Remark 3.1.If we consider the space independent case, by direct calculation it follows that conditionλ1>0 is equivalent toρerτ<1 and conditionλ1≥0 is equivalent toρerτ≤1,which is same as the Corollary 3.1 of[24].

Theorem 3.2.Suppose u0satisfies(H2),if λ1<0,the solutionˆu to(3.1)satisfies

where u*(x,t)is the extension by τ-periodicity of the unique non-negative solution to

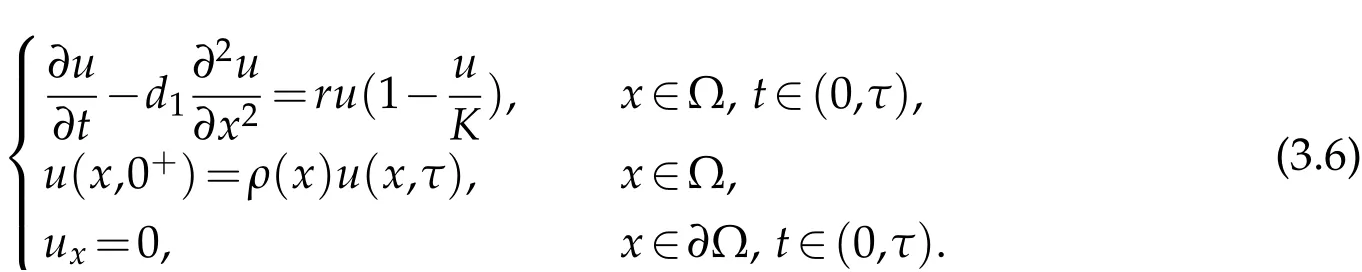
Proof.Ifλ1<0, we can deduce that:=∈ϕ1is subsolution of (3.6) for allwhereϕ1(x,t)is the principal eigenvector of(3.2),and satisfies

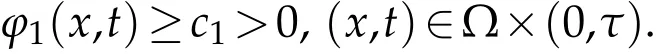
On the other hand,sinceρ(x)≤1,we can see thatρKis the supersolution of(3.6)for allρ>1.Thanks to comparison principle,we can get a unique non-negative solutionu*(x,t).Moreover we can choose∈ϕ1(x,0) as small andρKas large as we please, Applying the iteration scheme argument, we can get the global attractiveness ofu*(with respect to positive initial conditionsu0(x)).

4 Single species natural enemies model

Firstly,let us consider the following auxiliary problem:

wherevn(x,t)represents the density of the natural enemies population during periodn,vn,τ(x)denotes the density of the natural enemies population at timenτ,andv0=v0,τ(x).By calculation,the solution of the auxiliary problem(4.1)is expressed as

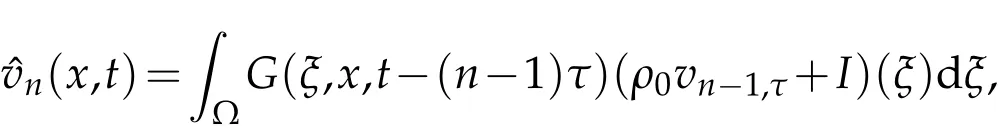
for allt∈((n−1)τ,nτ],where

We assumev0(x),I(x)∈L∞(Ω),then

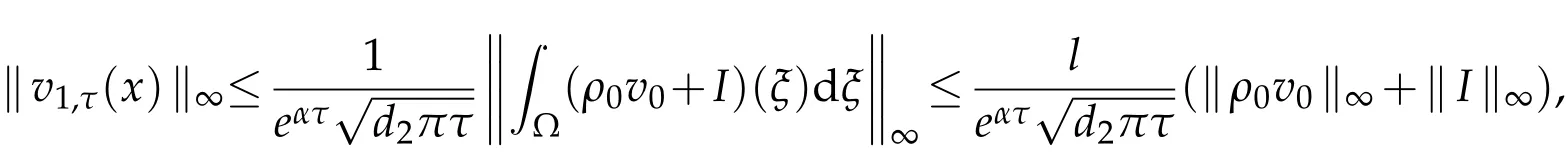
sov1,τ(x)∈L∞(Ω),and so onvn,τ(x)∈L∞(Ω),n∈N.

For anym>n∈N,

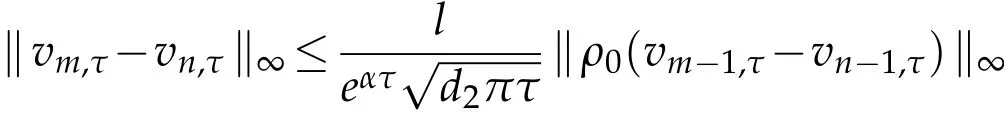
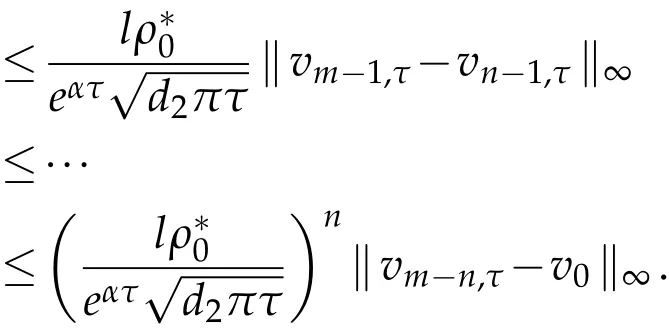
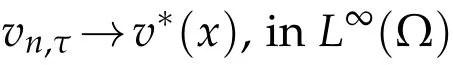
asn→∞,and

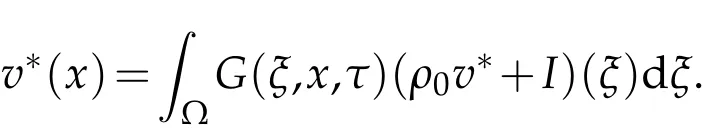
Now,we construct equation

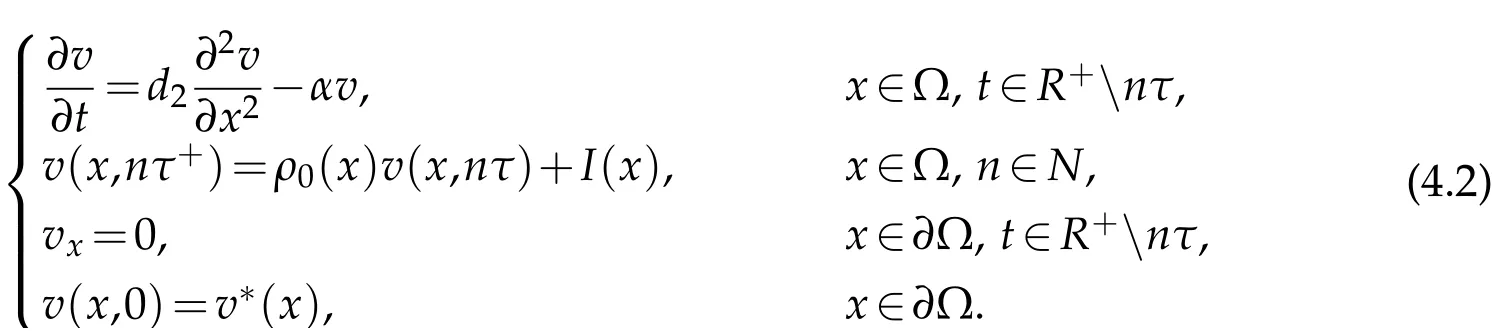
Thus,there is a unique non-negativeτ-periodicity solution ¯v(x,t),and

Then we get below Lemma.

Lemma 4.1.Ifthen the solutionvˆn(x,t)to(4.1)satisfies

as t→+∞.

Remark 4.1.If we consider the space independent case,then problem(4.1)becomes

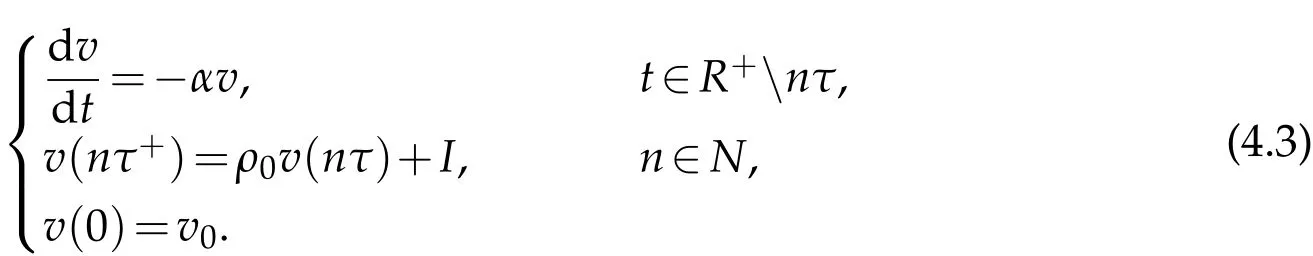
We can get the following result by direct calculation,

Corollary 4.1.If ρ0e−ατ<1,the solutionˆv(t)to(4.3)satisfies

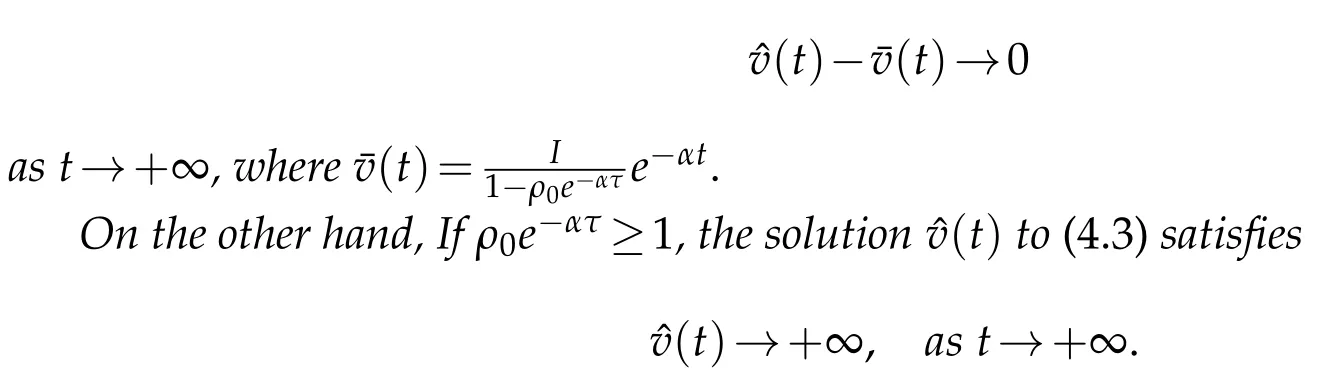
5 The boundary periodicity solution of the two species model

Firstly,the two eigenvalue problems are considered as follow

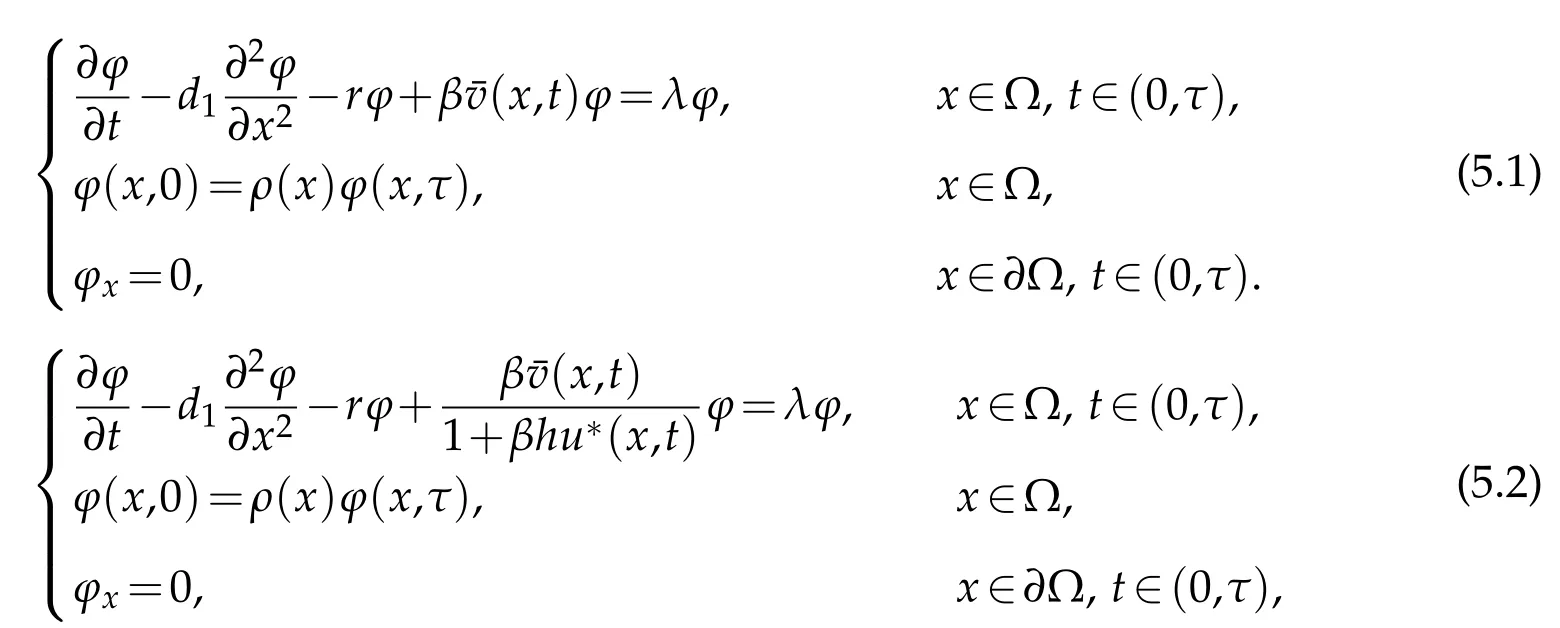
whereu*(x,t)is the extension byτ-periodicity of the unique non-negative solution to

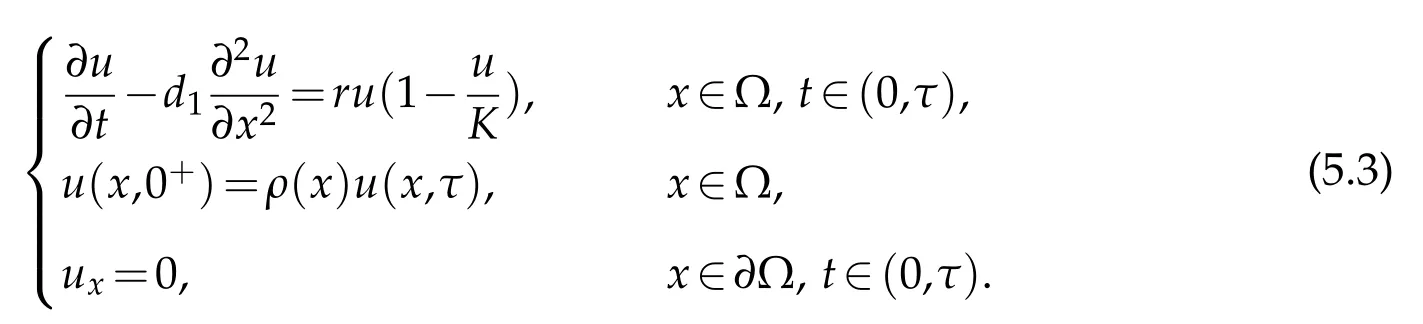
Supposeµ1,κ1be the principal eigenvalue to (5.1) and (5.2),respectively. It can be concluded thatκ1<µ1. we can deduce the following result.

Theorem 5.1.Suppose u0and v0satisfying(H2)andλ1<0, (i) the solution(u,v)to(2.1)satisfies:

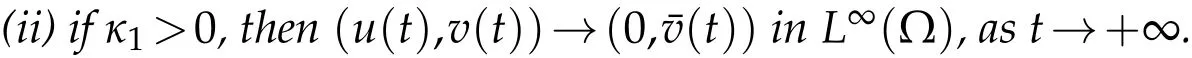
thenµ1≥0.Proof.(i)Supposeu(t)→0 inL∞(Ω),ast→+∞. Then,for any smallε>0,we can get

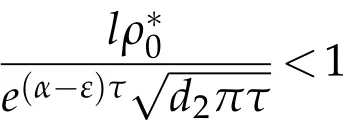
and also there existsN(ε)∈N,such that

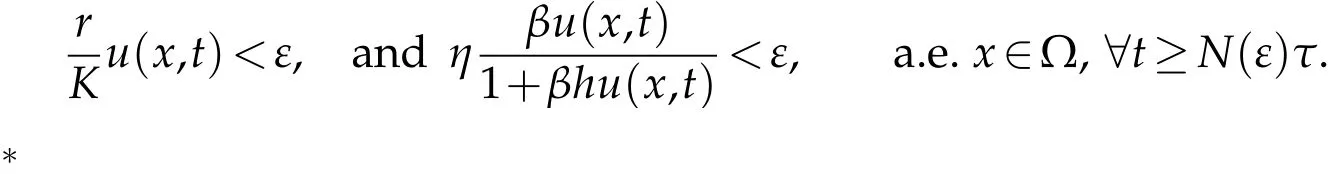
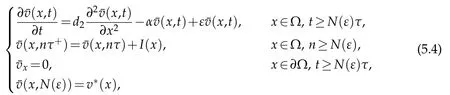
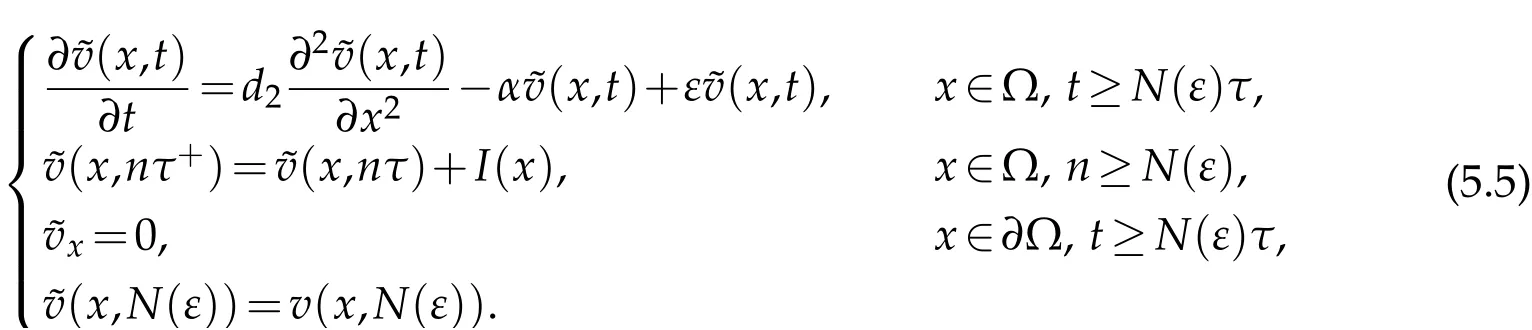
We get that

We may infer that fort≥N(ε)τ:I

n conclusion,

whereis the solution to

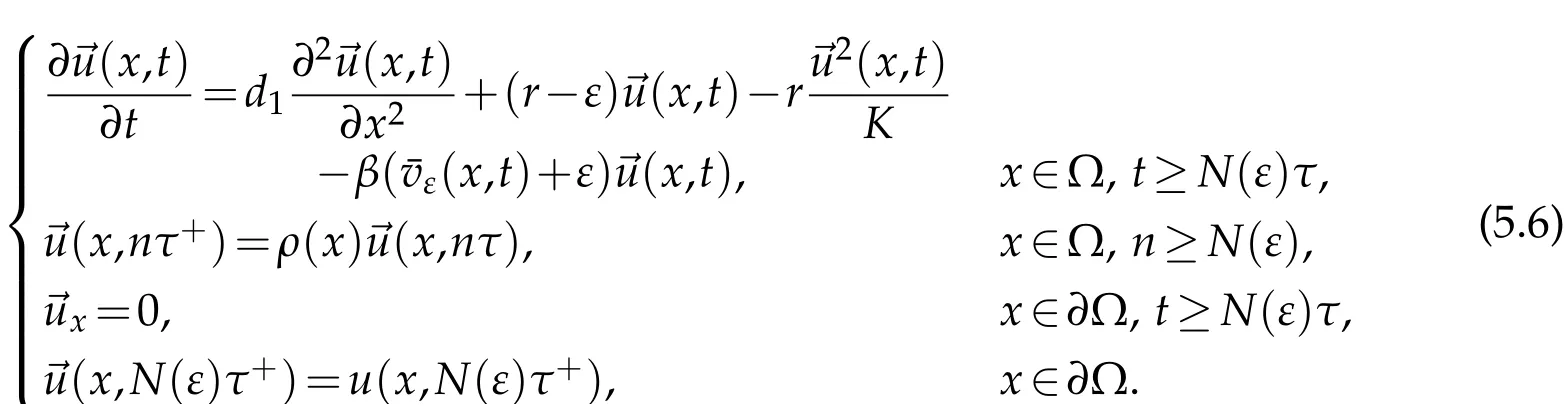
Sinceu(t)→0 inL∞(Ω),ast →+∞,we conclude that(t)→0 inL∞(Ω),ast →+∞and in the same manner as in Theorem 3.1 we get that

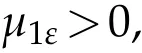
whereµ1ε>0 is the principal eigenvalue to (4.3), corresponding tor:=r−ε,(x,t):=

(ii) Suppose thatκ1>0. Ifλ1<0, Using a comparison result (see [27]), we get that there existsN1(ε)∈N,such that

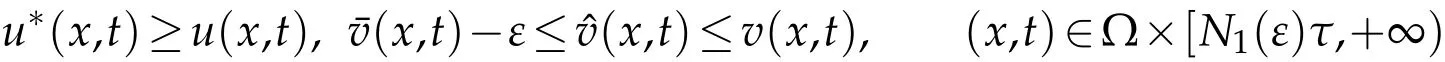
for arbitraryε>0, whereu*(x,t) is the extension byτ-periodicity of the unique nonnegative solution to(5.3),(x,t)is the solution of(3.6),(x,t)is the solution of(4.1). then

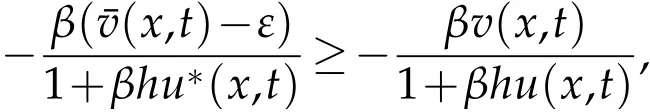
and so

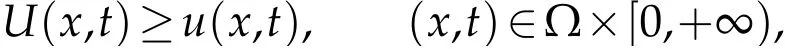
whereU(x,t)is the solution of

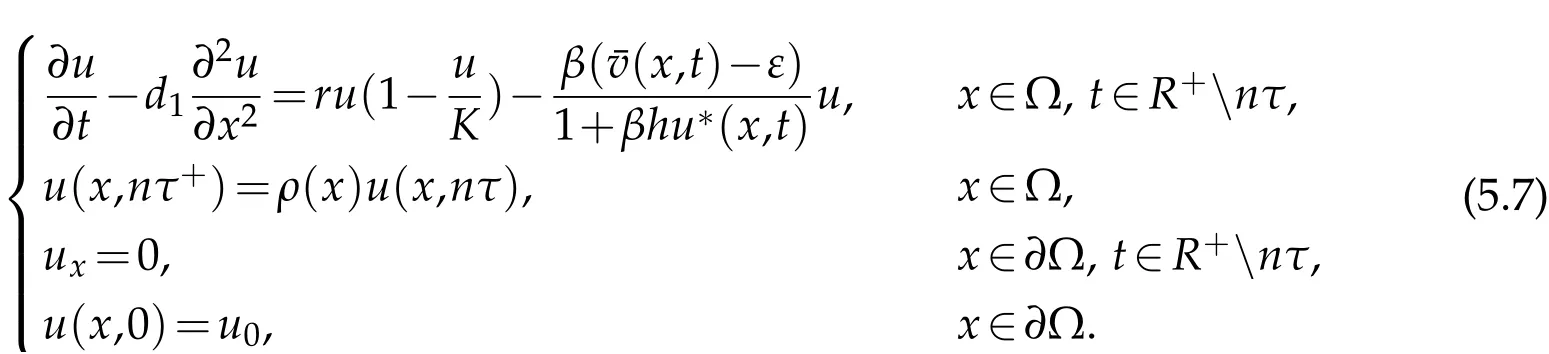
We can get

whereκ1εis the the principal eigenvalue to

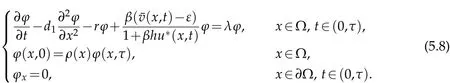
Sinceκ1>0,there exists very smallεsuch that

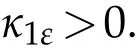
In the same manner as in Theorem 3.1,we get that

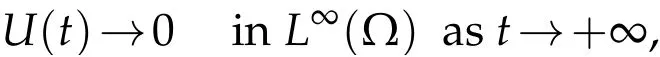
and consequently

Then,

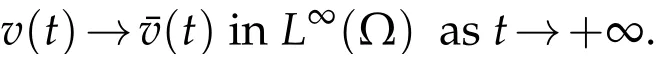
Remark 5.1.LetMis the maximum of ¯v(x,t),(x,t)∈Ω×(0,+∞),thenM=‖ρ0v*+I‖∞.If we assumedρ(x)=ρis a constant,we consider the following two eigenvalue problems:

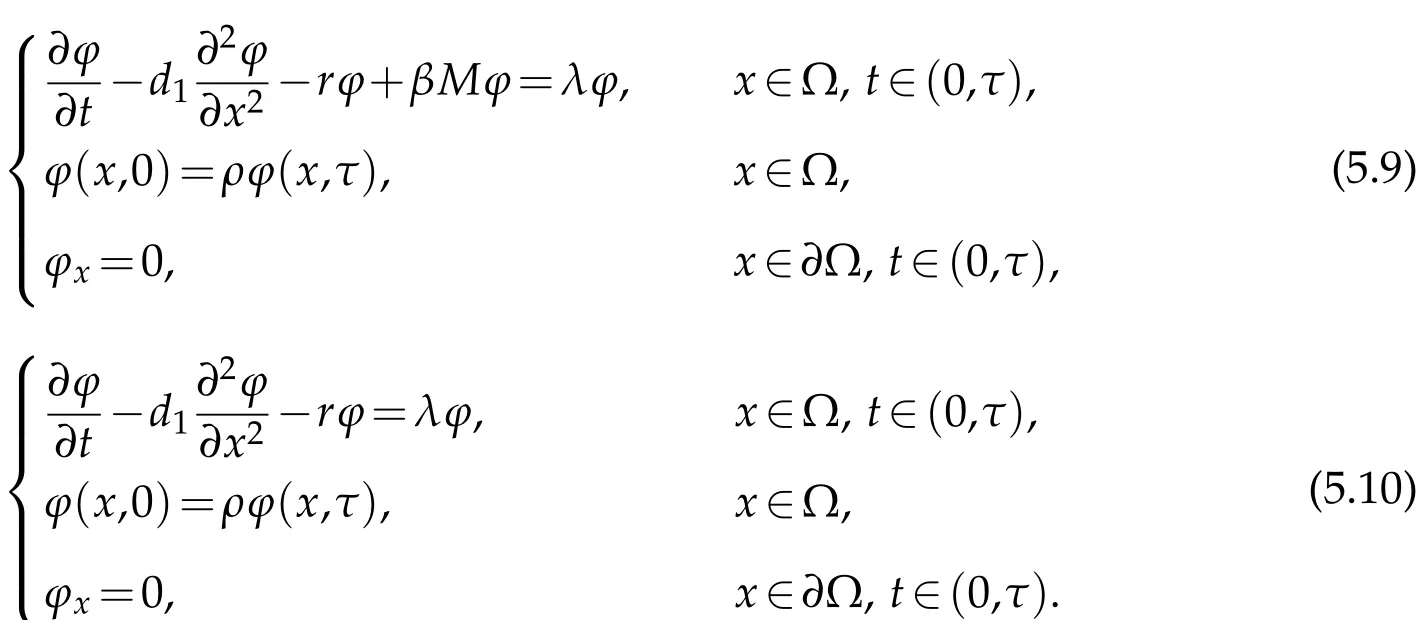
We can getζ1>κ1>µ1>ν1.Letζ1be the principal eigenvalue to(5.9)andν1be the principal eigenvalue to(5.10).

We can get the following corollary.

Corollary 5.1.The eigenvalue to(5.9)and(5.10)satisfies

Proof.Letϕ=e(λ+r−βM)tw,then problem(5.9)becomes

Using the method of separation of variables,we can get

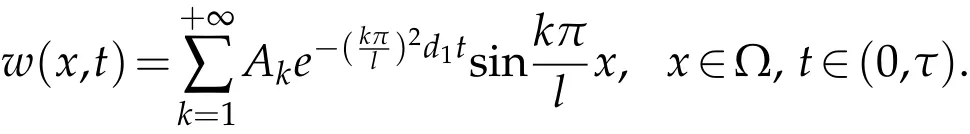
Use the conditionw(x,0)=ρe(λ+r−βM)τw(x,τ),we can get

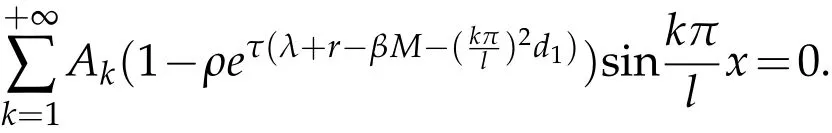
Multiply both sides with sin,and integral on(0,l),we can get

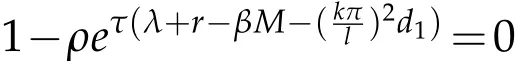
for allk∈N.So,ζksatisfies.Also,we can0 for the same methods.

According to Theorem 4.1,we can get the following corollary.

Corollary 5.2.Assume that. If ρ(x)=ρ is a constant and for any u0and v0satisfying(H2),the solution(u,v)to(2.1)satisfies:

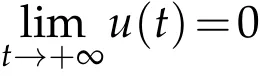
in L∞(Ω),then

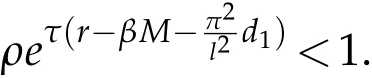
On the other hand,if

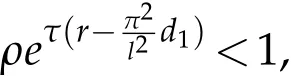
then for any u0and v0satisfying(H2),u(t)→0in L∞(Ω),as t→+∞.

Remark 5.2.If we consider the space independent case,then system(2.1)becomes

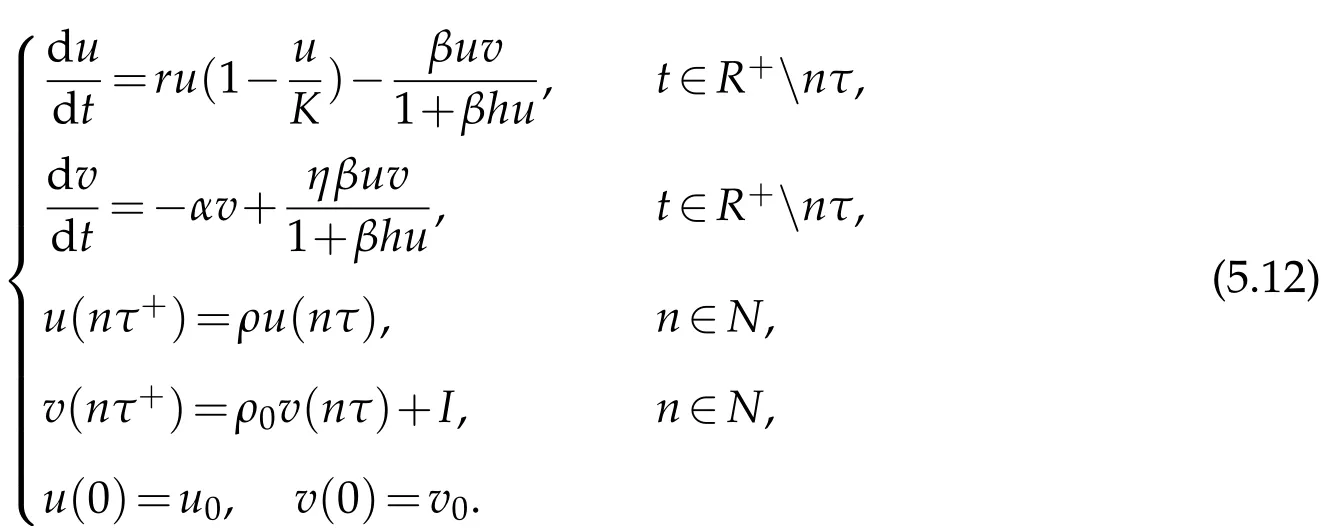
Finally,we obtain the following corollary.

Corollary 5.3.If ρ0e−ατ<1, for any u0and v0satisfying(H2), the solution(u,v)to(5.12)satisfies:

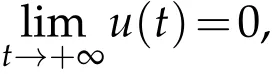
then

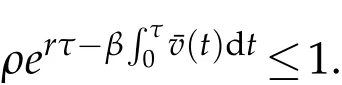
On the other hand,if

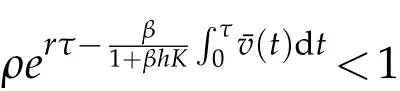
or

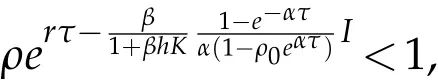
then for any u0and v0satisfying(H2), we have that u(t)→0, as t →+∞, where(u,v)is the solution to(5.12).

6 Simulations for the models

In order to verify the validity of the results,we consider system(2.1)withd1=d2=r=K=1,τ=2,β=h=α=η=1.Chooseρ=0.12,ρ0=0.8,obviously,we have that the parameters satisfy the condition of Corollary 5.2,

and

See Fig.1.Here we choosex∈Ω=(0,20)and the initial conditionu0(x)=v0(x)=e−(x−10)2,the natural enemy release functionI(x)=0.1 for allx ∈Ω.In this case, pests are extinct and natural enemies have a positive periodic solution.

If we chooseρ=0.12,ρ0=0.95,we have that the parameters satisfy the condition:

and

By numerical simulation, we can get the similar figure with Fig. 1. Here we give Fig.2. From Fig. 2, pests also are extinct and natural enemies also have a positive periodic solution. This means that the conditions in 5.2 are sufficient conditions,not necessary.

If we chooseρ=0.5,ρ0=0.8,we have that the parameters satisfy the condition:

and

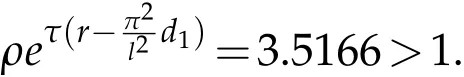
Form Fig. 3,pests and predators can coexist,all have positive periodic solutions.

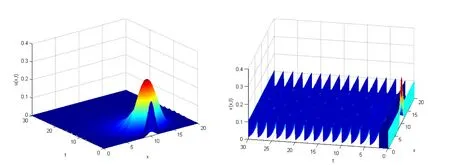
Figure 1: A numerical approximation to u and v with ρ=0.12,ρ0=0.8.

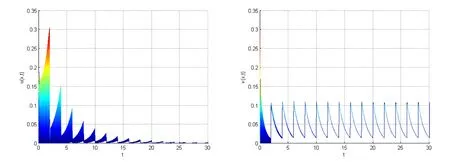
Figure 2: A numerical approximation to u and v at x=0 with ρ=0.12,ρ0=0.95.

7 Conclusion and discussion

In this article, we assume that the released natural enemies have less ability to adapt to new environment (intrinsic growth rate is less than zero) and uneven distribution of space(for convenience,assuming one dimensional space). Moreover,based on the control strategy of pest removal,the control strategy of natural enemies is added. At this point,the model is more reasonable and more applicable. It is found that the existence of the positive periodic solution of the single population pulse of natural enemy system is dependent of the release functionI(x), it is found that the increase of the release functionI(x)will cause the increase of the positive periodic solution. Meanwhile,the increase ofI(x)will indirectly make the condition of pest extinction easier to reach,which is straightforward to observe when the spatial distribution is uniform(Corollary 5.3). In addition,due to the complexity of partial differential equations,we do not find the explicit conditions for the extinction of pests,but when the survival rate of pests is constant,we get the explicit sufficient condition and necessary conditions for the extinction of pests, which makes our conclusions more practical(Corollary5.2).

Figure 3: A numerical approximation to u and v with ρ=0.5,ρ0=0.8.

Functional response of natural enemies and boundary condition

We use Holling II type functional response to describe the interaction between pest and natural enemies,when the handing time equals zero,the functional response is the simplest form. Moreover,the functional response can also be changed to Holling III and IV,and the conclusions are similar.

We assume that the second type of boundary condition holds for the pest and natural enemy population, model with the third types of boundary can also be discussed with the same methods.

The direction of later research

In the model, pulse control occurs which involves release of natural enemies and spraying pesticides in a fixed time. In fact,it can be improved to other two forms:

(a)spraying pesticides more(less)frequently than releasing natural enemies;

(b)releasing natural enemies and spraying pesticides only when pest densities reach their economic threshold (ET) [16]. And all of these can be used as a direction for later research.

Acknowledgement

The author wishes to express their gratitude to the editors and the reviewers for the helpful comments. The work is supported by the NSFC (11831003, 11771031, 11531010) of China, NSF of Qinghai Province (2017-ZJ-908), the young backbone teachers project of undergraduate universities of Henan Province in 2021, the science and technology key project of Henan Province of China under Grants(212102310464,182102110292)and Key Scientific Research Project of Higher Education Institutions of Henan Province(21A110015).