Blow-up of Classical Solutions to the Isentropic Compressible Barotropic Navier-Stokes-Langevin-Korteweg Equations

HU Ke

School of Mathematical Sciences,Fudan University,Shanghai 200433,China.

Abstract. In this paper, we study the barotropic Navier-Stokes-Langevin-Korteweg system in R3. Assuming the derivatives of the square root of the density and the velocity field decay to zero at infinity,we can prove the classical solutions blow up in finite time when the initial energy has a certain upper bound. We obtain this blow up result by a contradiction argument based on the conservation of the total mass and the total quasi momentum.

AMS Subject Classifications:35Q35,35B44

Key Words: Navier-Stokes-Langevin-Korteweg system;classical solutions;blow up.

1 Introduction

We are concerned with the Cauchy problem for the isentropic compressible barotropic Navier-Stokes-Langevin-Korteweg system in R3:

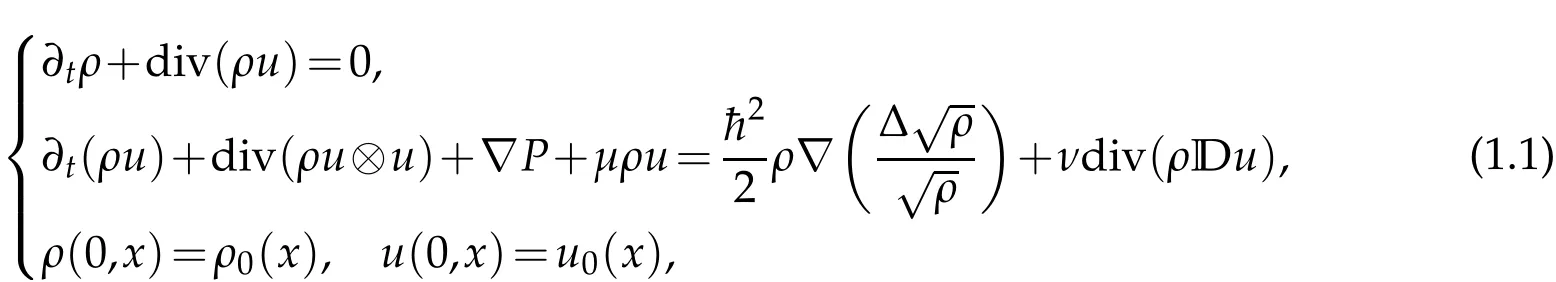
where Du=(▽u+▽u⊤)/2,the unknown functionsρ:R+×R3→R+andu:R+×R3→R3denote the density and the velocity field respectively, andP:R+×R3→R+is the barotropic pressure of the formP(ρ)=ργwhereγ>1 is the adiabatic constant.µ>0,¯h>0 andν>0 are the dissipation coefficient, the renormalized Plauck constant and the viscosity coefficient respectively.

The Navier-Stokes-Langevin-Korteweg equations include many classical equations,such as the compressible Navier-Stokes equations ifµ=¯h=0 which describe the law of mechanics of viscous fluids and are significant in fluid mechanics; the Navier-Stokes-Korteweg equations ifµ=0 which are firstly considered by Van der Waal and Korteweg to model fluid capillarity effect and then developed by Dunn and Serrin[1]to reflect the variation of density at the interface of two phases; the Euler-Langevin-Korteweg equations ifν=0 which are firstly used as a stochastic interpretation of quantum mechanics[2],then applied to quantum semiconductor[3]and quantum trajectories of Bohmia mechanics[4],and recently have a renewed interest in statistical mechanics and cosmology[5].

There are many theoretical studies in blow up of smooth solutions of compressible Navier-Stokes equations. In 1998, Xin [6] showed a sufficient condition which leads to blow up of smooth solutions with initial density of compact support, and the key idea of proof is the total pressure decays faster in time in the presence of the vacuum. Then these results were improved by Xin and Wei [7] by showing the finite time blow up of smooth solutions with initial density containing vacuum and without the assumption of finite total energy. For the same questions, Lai [8] applied a contradiction argument to prove the classical solutions blow up in finite time, when the gradient of the velocity satisfies some decay constraint and the initial total momentum does not vanish. The blow up results of the full compressible case and the isentropic compressible case with constant and degenerate viscosities are obtained by Jiu [9], and a more precise blow up time can be computed out when the results are applied to Euler equations. Huang [10]presented a blow-up criterion for classical solutions in R3in terms of the gradient of the velocity, which is the necessary condition of blow up. For the Navier-Stokes-Korteweg system, Tang [11] established a blow up result for the smooth solutions to the Cauchy problem of the symmetric barotropic case with initial density of compact support. The one-dimensional initial boundary value problem in a bounded domain was studied by Tang[12] and the blow up results of smooth solutions were obtained. Li[13] showed a Serrins type blow-up criterion for the density-dependent Navier-Stokes-Korteweg equations with vacuum in R3.

To our best knowledge,there isn’t any blow up result for the Navier-Stokes-Langevin-Korteweg system yet and the dissipative termµρuon the left side of(1.1)2brings some difficulties when we come to prove the total momentum is conserved.To overcome these difficulties,we define the total quasi momentum as

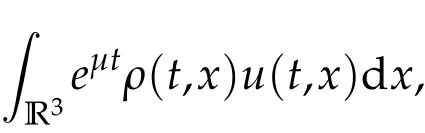
and we prove the classic solutions to the three-dimensional Navier-Stokes-Langevin-Korteweg system blow up in finite time by a contradiction argument based on the conservation of the total mass and the total quasi momentum in this paper.

Remark 1.1.Meanwhile,there are a lot of results on existence of weak solutions to these equations.Readers can refer to[14-20]if they have interest.

We now introduce the definition of classic solutions and state the main result of this paper.

Definition 1.1.Let T>0. We call(ρ(t,x),u(t,x))are clssical solutions to the barotropic Navier-Stokes-Langevin-Korteweg system(1.1)on[0,T)×R3if

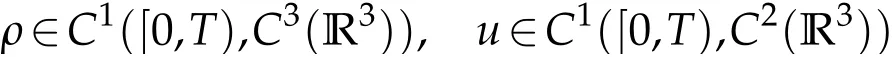
and satisfy(1.1)on[0,T)×R3pointwisely.

Theorem 1.1.Support that(ρ,u)are classical solutions of the barotropic Navier-Stokes-Langevin-Korteweg system(1.1)withµ>0,ν>0. We assume that

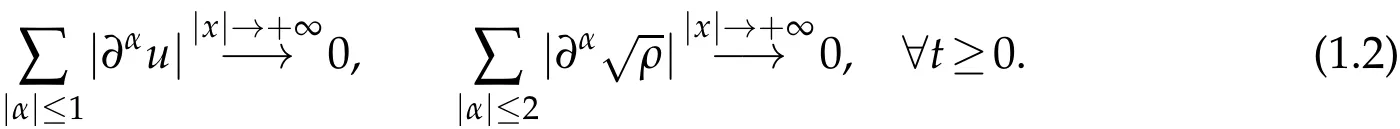
Moreover,ρ satisfies

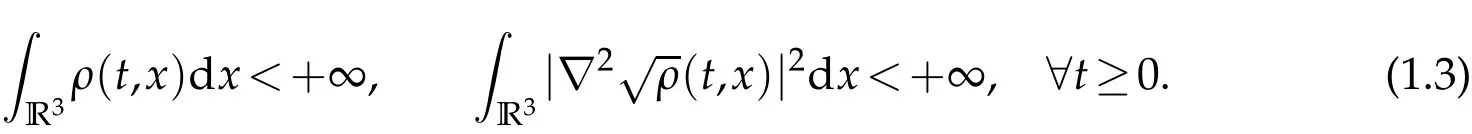
If the initial data satisfies

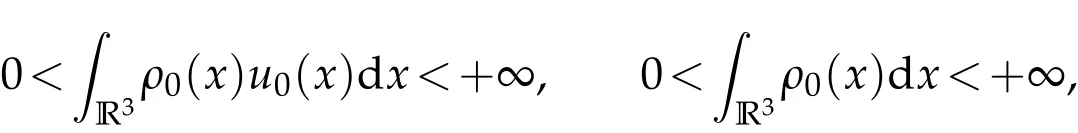
and the initial energy satisfies

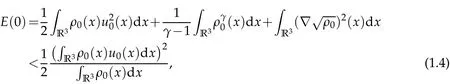
then the classical solutions of system(1.1)will blow up in a finite time T*.

Remark 1.2.Our method also works for other dimensions(n≥2).

2 Preliminaries

We first give three lemmas showing the energy estimate and stating the conservation of the total mass and the total quasi momentum before demonstrating the proof of the main theorem.

Lemma 2.1.Support that(ρ,u)are classical solutions of system(1.1)and satisfy(1.2),then we have the energy estimate for t∈(0,T*)

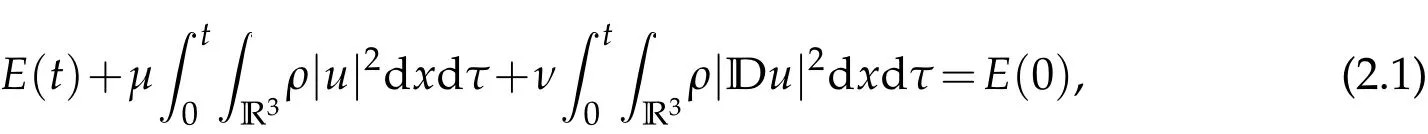
where E(t)is the total energy

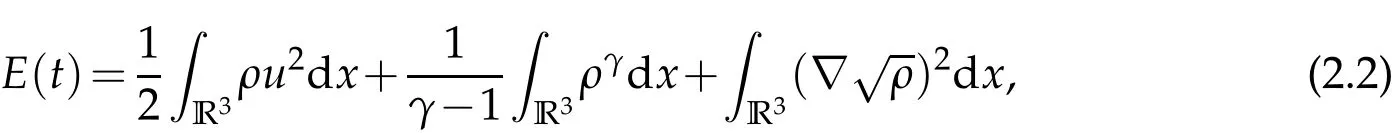
and T*denotes the lifespan of classical solutions.

Proof.Multiplying(1.1)2withuand using(1.1)1twice,we have

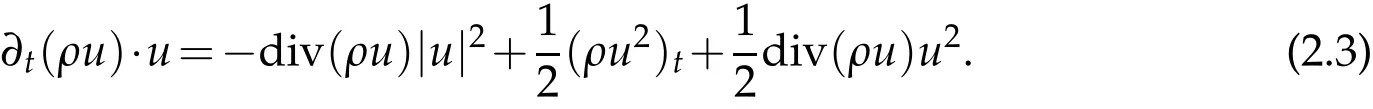
And it is easy to obtain

From(1.1)1,we have

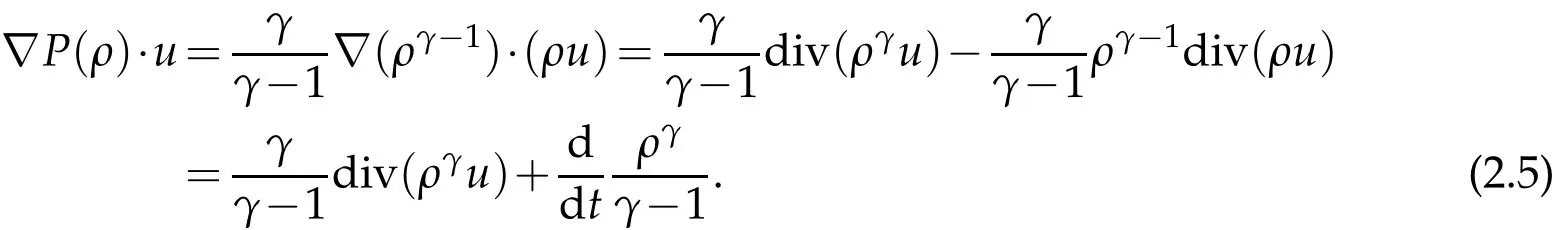
Using(1.1)1again,we get

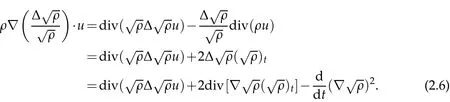
And it is obvious that

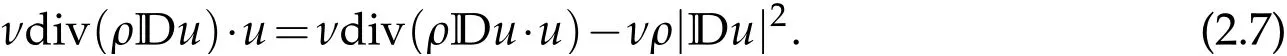
Combing(2.3)-(2.7),we have

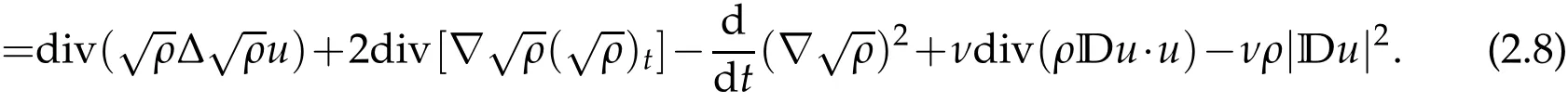
Integrating(2.8)over R3,and according to the assumption(1.2),we get

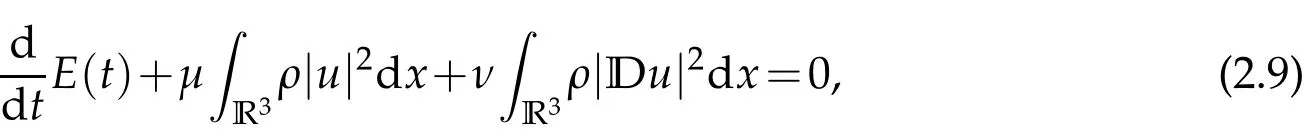
where

Integrating(2.9)over[0,t],we come to

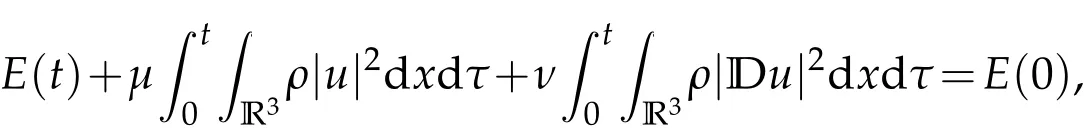
and the proof of Lemma 2.1 is finished.

Since the initial energy is finite,we can assert that

are all finite.

Lemma 2.2.Support that(ρ,u)are classical solutions of system(1.1)and satisfy∫R3ρ(t,x)dx<+∞,then the total mass of this system is conserved in the sense that

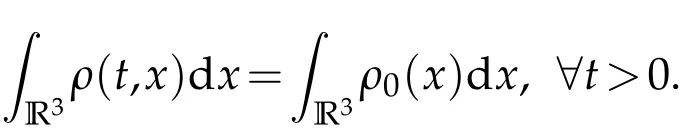
Proof.Integrating(1.1)1over[0,t]×BR={(τ,x)∈R+×R3|0≤τ≤t,|x|≤R},we yield

Using H¨older’s inequality and the assumption that ∫

R3ρ(t,x)dx<+∞,we have

which means that for any fixedt>0,

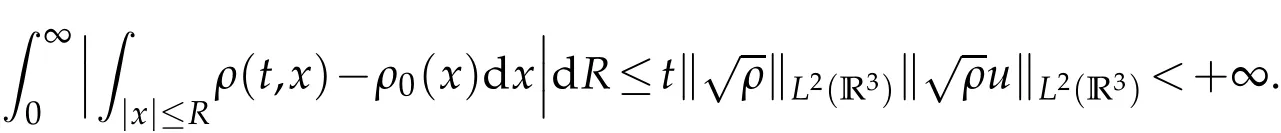
which is

and the proof of Lemma 2.2 is finished.

Next we will state the conservation of the total quasi momentum ∫

R3eµtρ(t,x)u(t,x)dx.

Lemma 2.3.Support that(ρ,u)are classical solutions of system(1.1)and satisfy(1.3),then the total quasi momentum of this system is conserved in the sense that

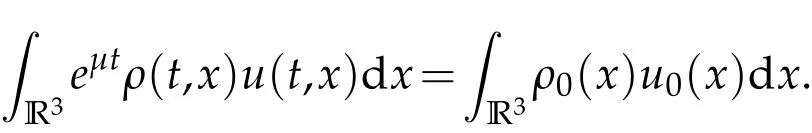
Proof.Multiplying(1.1)2witheµt,we yield

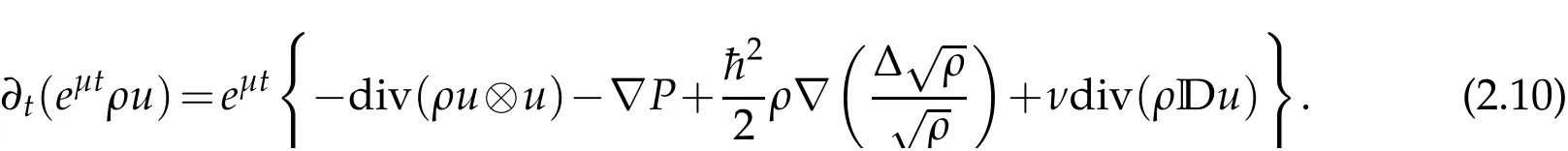
Integrating(2.10)over[0,t]×BR,we have

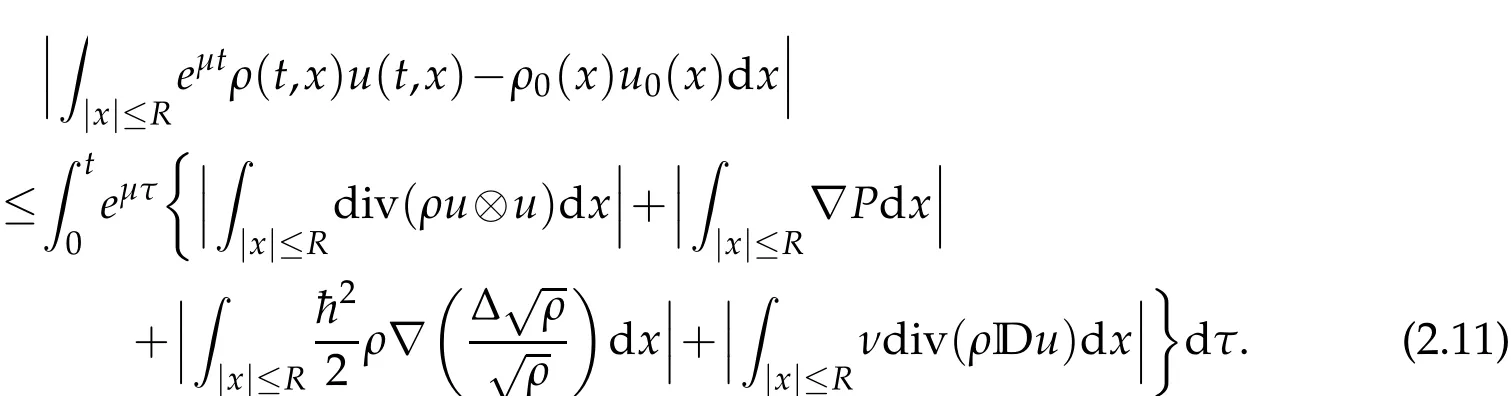
Integrating(2.11)over(0,+∞)with respect toR,we notice that

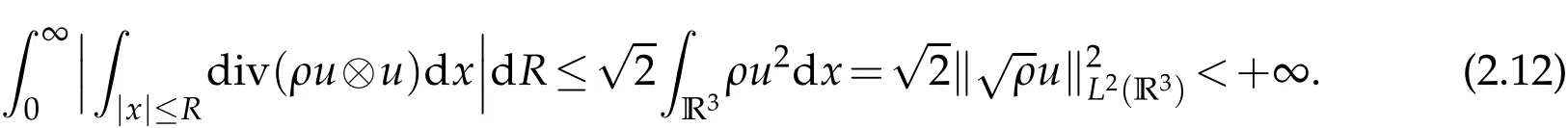
By using the Gauss’s formula,we have

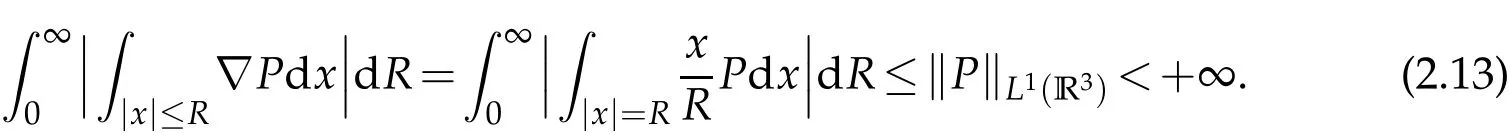
According to the assumption(1.3),we get

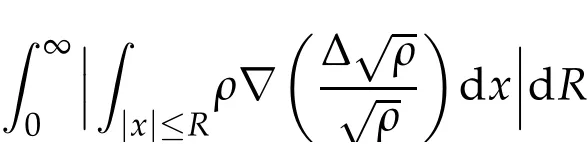
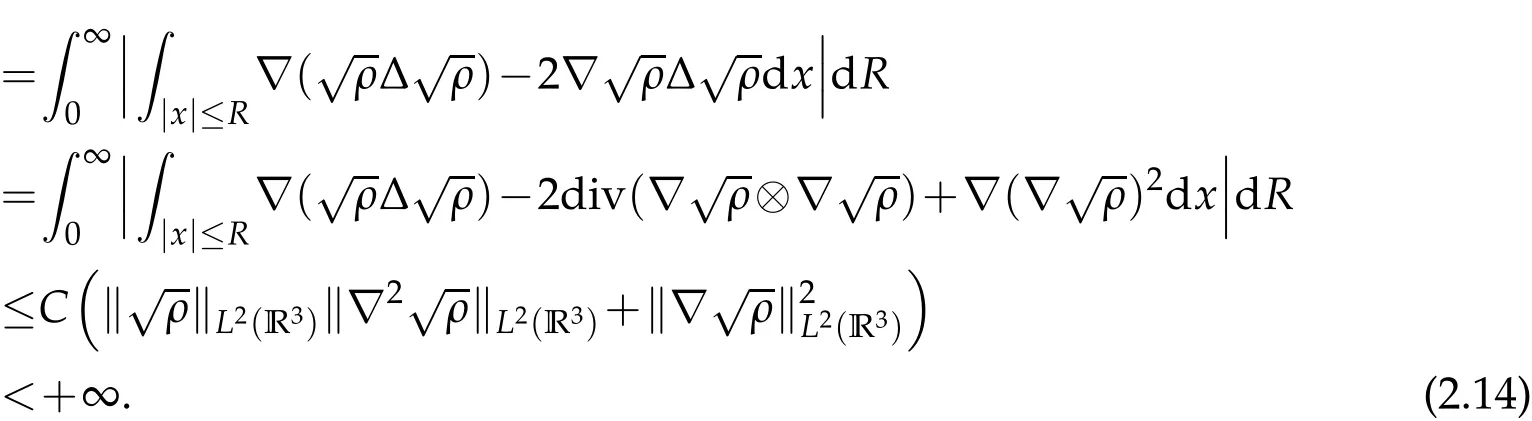
Then using the assumption that ∫

R3ρ(x)dx<+∞,we yield

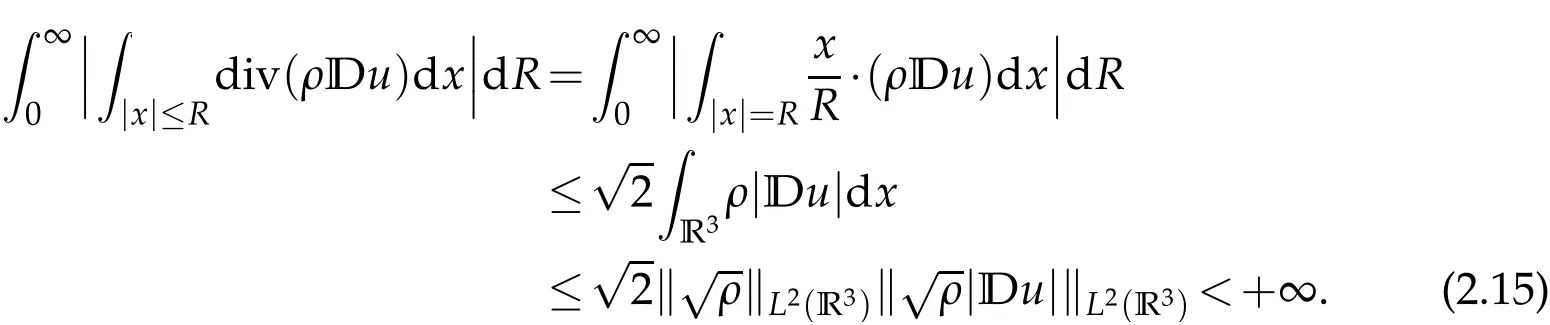
Combining(2.11)-(2.15),we can obtain that for any fixedt>0,

where

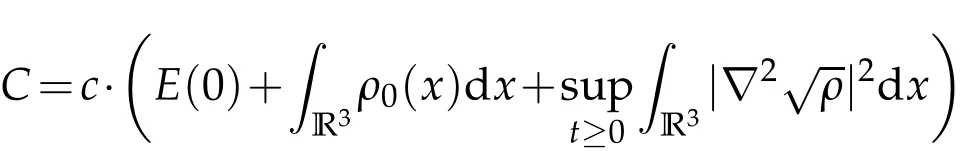
andcis a positive constant.Hence,we come to

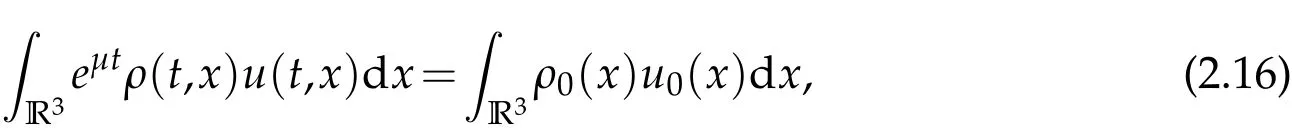
and the proof of Lemma 2.3 is finished.

3 Proof of the main theorem

In this section, we are going to prove Theorem 1.1 by a contradiction argument. On account of Lemma 2.2 and Lemma 2.3,we have

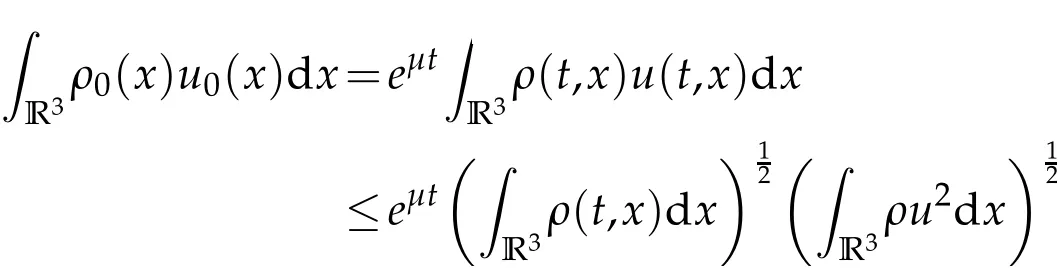
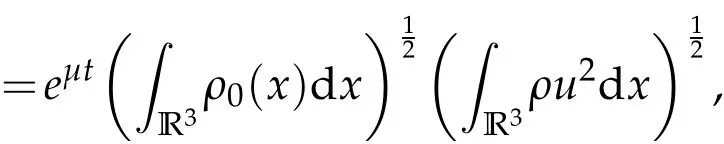
which means

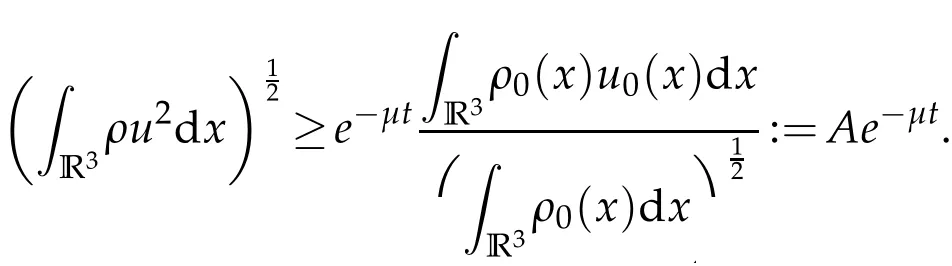
Hence we have

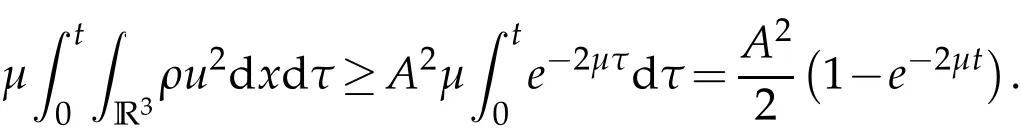
Using the assumption(1.4)thatE(0)

Substituting this result into(2.1),we obtain there isT*∈(0,T)such thatE(T*)=0 which contradicts to the conservation of the total mass,and the proof of Theorem 1.1 is finished.