Theory and Applications of Distinctive Conformable Triple Laplace and Sumudu Transforms Decomposition Methods
BHANOTAR Shailesh A.and BELGACEM Fethi Bin Muhammad
1 Department of Mathematics,LJIET,L J University,Ahmedabad,Gujarat,India.
2 Department of Mathematics,Faculty of Basic Education,PAAET,Al-Ardiya,Kuwait.
Abstract. This article presents some important results of conformable fractional partial derivatives. The conformable triple Laplace and Sumudu transform are coupled with the Adomian decomposition method where a new method is proposed to solve nonlinear partial differential equations in 3-space. Moreover, mathematical experiments are provided to verify the performance of the proposed method. A fundamental question that is treated in this work: is whether using the Laplace and Sumudu transforms yield the same results? This question is amply answered in the realm of the proposed applications.
AMS Subject Classifications: 35A25,35M12,35Q40,35R11.
Key Words: Riemann-Liouville fractional integral;fractional derivative;Adomian decomposition method;conformable fractional partial derivative;conformable triple Laplace and Sumudu transform.*Corresponding author.Email addresses:sbhanotar@gmail.com(Shailesh A.Bhanotar),fbmbelgacem@gmail.com(Fethi Bin Muhammad Belgacem)
1 Introduction
In recent years, it has been found that fractional partial differential equations (FPDEs)are very important for modelling many Real-life sciences and engineering applications, such as fluid dynamics, biology of mathematics, electrical circuits, optics, Quantum Mechanics, etc. [1-3]. Many definitions of fractional derivatives and integrals, such as Rizez, Weyl, Riemann-Liouville, Caputo, Hadamard and so on, have been mentioned in literature. These forms of fractional derivatives have many peculiar properties such as not all two functions follow chain rule, product, and quotient rule, these significant properties lead to some flaws in physics and engineering applications. In 2014, Khalil et. al[4]introduced a new type of derivative called the conformable fractional derivative(CFD)which satisfies the classical properties of the known derivative. The conformable fractional derivative of functionf:(0,∞)→R,of orderα∈(0,1]is defined by,
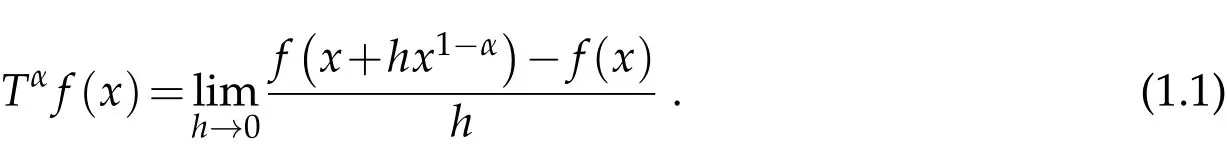
Many analytical and numerical methods for accurate and approximate solutions have been developed by several researchers over the last few years,such as the Tanh method[5],Reliable methods[6],Exponential rational function method[7],Kudryashov method[8],Simplest equation method(SEM)[9],Single conformable Laplace transform method(CLT) [10], single conformable Laplace transform method (CLT) [10], conformable double Laplace transform(CDLT)[11,12],conformable triple Laplace transform and Sumudu transform [34,35], double Shehu transform [13], and some critical analyses about conformable fractional[20].
Watugala [14], implemented a new integral transformation at the beginning of the 1990s, called the Sumudu transformation(ST),which derived from the classical Fourier Transform,and applied it to obtain the solution of many problems in real life science and engineering. Infect, it is proved to be an efficient method for solving physical problems because of its unit and scale preserving properties. For more about (ST) see[15,16],authors have studied about properties of Sumudu transform and[17,18]application of Sumudu transform(ST)and Laplace transform(LT).
The transformation of Sumudu is defined in the set of functions[33],
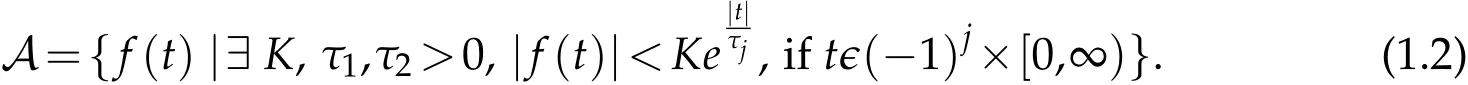
By the following formula,
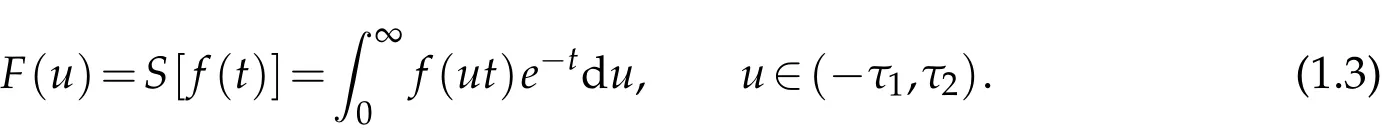
The authors in [19,21] recently introduced the single and double conformable Sumudu transform(CST)in 2019-20. Ibrahim et.al[36-38],have explored operator for symmetric conformable fractional derivative of complex variable and on quantum hybrid fractional conformable differential in a complex domain,in[39,40],on subclasses of analytic functions based on a quantum symmetric and the generalized wave dynamical equations based on time space symmetric differential equation operator, respectively, and Moreover, in [41], some fixed-point theorems for almost weak contraction in S- metric space via conformable fractional operator. In order to solve linear fractional partial differential equations in the conformable fractional derivative sense,we implement the conformable Triple Sumudu transform(CDST)due to the certain benefits of Sumudu transformation(ST) over Laplace Transformation (LT). After referring literature, we come up with the idea to study the nonlinear partial fractional differential equations by defining a function in three-dimensional space. Therefore, a Conformable triple Sumudu transform is defined and coupled with Adomian decomposition method to solve systematic nonlinear partial fractional differential equations. The main advantage of this method will give accurate solutions to nonlinear partial fractional derivatives in three dimensional space.One thing you will be able to get the answer of question asked by Atangana et al. [31],in his paper.
This paper is divided into the following sections: In Section 2, some basic Fractional calculus concept has been discussed on conformable partial derivatives. In Sections 3 and 4, the main results and theorems on the conformable triple Sumudu and Laplace transforms are investigated respectively. In Section 5, Sumudu and Laplace transform Adomian decomposition methods for a general nonhomogeneous partial fractional differential equation are given. In Section 6, numerical experiment is conducted using the proposed method to validate the obtained results,analyzed and presented plots for different parameters. In Section 7,a conclusion of our research work is provided.
2 Preliminary
The basic definitions and properties of the fractional calculus theory are provided in this section,which are further used in this paper.
Definition 2.1.The Riemann-Liouville fractional integral operator of order γ>0, for t>0is defined by

And the Riemann-Liouville derivative of order γ>0is given by

where n −1<γ When attempting to model real-world phenomena with fractional differential equations, the Riemann-Liouville derivative has a certain drawback. We shall therefore implement an updated fractional differential operator suggested by M. Caputo in his dissertation on viscoelasticity theory[25]. The properties of the operatorJγcan be found, where the gamma function is Γ(γ),γ>0 andt>0. Definition 2.2.The Caputo fractional derivative of f(t)of order γ>0with t>0is defined as,for m−1<γ≤m,m∈N. Definition 2.3.(see [32]). Given a function f:R+×R+×R+→R, the conformable partialfractional derivatives (CPFDs) of order α,β and γ of the functionis defined asfollows: whereare called the fractional partialderivatives of order α,β,and γ,respectively. We prove the basic Theorem 2.1, and the relation between the CPFDs and partial derivatives as follows: Theorem 2.1.Let α,β,γ∈(0,1]and f(x,y,t)be a differentiable at a point for x,y,t>0. Then, Proof.By the definition of CFPD, Similarity,we can prove the results(2)and(3). In the next proposition, we mention the conformable partial fractional derivative of some functions. By using Theorem 2.1,it can be verified easily. Proposition 2.1.Let α,β,γ∈(0,1]and a,b∈R,l,m,n∈N;Then,we have the followings: Proof.It can be easily verified with the help of Theorem 2.1. In this section,we recall some basic definitions on fractional conformable Laplace transform and some results which will be used later on. Also, we define conformable triple Laplace transform. For more details see[25-30]. Definition 3.1.Let the function u:(0,∞)→R and0<α≤1be the piecewise continuous function.Then, the conformable Laplace Transform (CLT) of functionof exponential of order, isdefined and denoted by, Definition 3.2.Let u(x,y)be a piece wise continuous function on the domain D of R+×R+ofexponential order. Then Fractional conformable double Laplace Transform(FCDLT)ofis defined and denoted by,wherep,q∈C,α,β∈(0,1]. Now, we define fractional conformable triple Laplace transform, forα,β,γ ∈(0,1], andp,q∈C are the Laplace variables. Definition 3.3.Let ube a real valued piecewise continuous function of x,y and tdefined on the domainDof R+×R+×R+of exponential order. Then,the fractional conformabletriple Laplace transform(FCTLT)of uis defined as follows: where p,q,s∈C,are Laplace variables of and respectively and α,β,γ∈(0,1]. The fractional conformable inverse triple Laplace transform,denoted byis defined by, Definition 3.4A unit step or Heaviside unit step function is defined as follows: Theorem 3.1.If,and=Vα,β,γ(p,q,s)andA,BandCare constants then the followings hold: whereΓ(·)Is the gamma function. Note thatΓ(n+1)=n!,forn=0,1,2,3,... 4. The First Shifting theorem for conformable triple Laplace transform: Proof.It can be proved using definition of Triple Laplace transform. Theorem 3.2.If(p,q,s),then where H(x,y,t)is a Heaviside unit step function as defined in eq.(3.3). Proof.By applying the definition of CTLT, Now,using definition of Heaviside Unit step functionH(x,y,t),we have which gives, This completes the proof of the theorem. Theorem 3.3.IfThen the fractional conformable tripleLaplace transform of the functionandare given by, Proof.It can be easily verified with the help of definition of triple Laplace transform. Theorem 3.4.For α,β,γ∈(0,1].Letbe the real valued piece-wise continuous func-tion defined on the domain(0,∞)×(0,∞)×(0,∞).The FCTLT (Fractional Conformable triple Laplace transform)of the conformable partial fractional derivatives of order α,β,and γ,then Proof.Here we go for proof of result(1),and the remaining results(2-7)can be proved. To obtain fractional conformable Triple Laplace transform of the fractional partial derivatives,we use integration by parts and Theorem 2.1. By applying the definition of FCTLT,we have Therefore,Eq. (3.4)becomes, The integral inside the bracket is given by, By substituting Eq. (3.6)in Eq. (3.5),and simplifying,we get the required result(1). That is, This completes the proof of the theorem. In general,the above results can be extended as, and In this section,we recall definition of Sumudu transform and defined conformable triple Sumudu transform and some important results on it and based on these results we will introduce new method to solve linear and nonlinear dynamic Partial fractional differential equation. Definition 4.1.The conformable fractional Sumudu Transform (CFST) of functiondefined over the set, And defined by the integral, Or equivalently, where p∈Cis the Sumudu variable correspond to x. Definition 4.2.([32])Letbe a piecewise continuous function on the domain D ofR+×R+. Then conformable fractional double Sumudu Transform(CFDST)ofis de-fined over the set: By the integral, where,and p,q are the transform variable of x and y accordingly. Definition 4.3.The fractional conformable partial Sumudu transformation of a piecewise continuous real valued function u:R+×R+×R+→R, is defined as follows and it can be extended over the set as it is mentioned in Eq.(4.1): Now,we define Conformable triple Sumudu transform,forα,β,γ∈(0,1],andp,q,s∈C are the transformable or Sumudu variables of positivex,yandtrespectively. Definition 4.4.Letbe a real valued piece wise continuous function defined on thedomain D of R+×R+×R+of exponential order. Then,the fractional conformable triple Sumudutransform(FCTST)ofis defined as follows: The conformable inverse triple Sumudu transform is defined by, Remark 4.1.The existence condition for the Conformable triple Sumudu transform. Ifuis an exponential ordera,bandcthen there existK>0,for allsuch that And we write, Equivalently, It means, the functiondoes not grow faster thanas Theorem 4.1.Let u and v:R+→R be the given functions,and for α,β,γ∈(0,1]. Ifand A,B and C are constants. Then the conformable triple Sumudu transform of some functions are given by, 3.isthe gamma function. Note thatΓ(n+1)=n!,forn=0,1,2,3,... Proof.It can be verify with the help of definition of Triple Sumudu Transform. Theorem 4.2.Ifthen the conformable frac-tional triple Sumudu Transform of the functions,are given by, Proof.Here we prove results 1,4,and 6. Remaining can be proved similar manner. By definition of Fractional Conformable triple Sumudu transform,we have, Differentiating Eq. (4.7)with respect to′p′, We partially differentiate inside the brackets, Substituting eq. (4.9)in eq. (4.8). we have, which gives, Hence the result(1)proved. To prove result(4), we need to partially differentiate of eq. (4.7)with respect to‘p’twice. We can get, Using eq. (4.7)in eq. (4.11)and simplifying,we have, Hence the result(4)is proved. Now to prove the result(6),we differentiate partially of Eq. (4.7)with respect top,qandsrespectively,we have, Therefore, Using the results of Theorem 4.2(Results-1-5)and Simplifying,we get, Hence,the result(6)is proved. Theorem 4.3.For0<α,β,γ ≤1, the Conformable fractional triple Sumudu transformation ofcan be represented as follows: Proof.(1)By applying the definition of CFTST,we get, Using the integration by part rule,Eq. (4.15)reduces to, which complete the proof(1). Similarly,result(2)and(3)can be proved. The following lemma also can be proved by similar way. Lemma 4.1.Ifthe conformable fractional triple Sumudutransform of theis given by: For0<α,β,γ≤1, Proof.The proof can be followed from Theorem 4.3. In general, the above lemma can be extended as follows and it can be verified by mathematical induction: The following theorem gives the conformable triple Sumudu transform of the fractional partial derivativesand Theorem 4.4.LetIf the conformable triple Sumudu trans-form of the functionandare given by: For0<α,β,γ≤1. Proof.By using the definition of triple Sumudu transform,we have Now differentiating with respect top,we get Therefore, We use Theorem 4.3 and simplifying,we get Hence,result-1 is proved. In a similar manner,one can prove result-2. In this section we propose conformable triple Sumudu Adomian decomposition method.Similarly,conformable triple Laplace Adomian decomposition method can be followed.Consider nonlinear non homogeneous partial fractional differential equation, wherem=1,2,3,...and γ∈(0,1]with the initial conditions, where R is the linear differential operator, N addresses the non-Linear partial fractional operator and,is the source term. To solve equation(5.1)follow the following steps: Step 1:Take fractional conformable triple Sumudu Transform to the Eq. (5.1)on both sides,and applying standard result. we have, Step 2:Using the derived result and applying the fractional conformable inverse triple Sumudu transform. we get, whereG(x,y,t) represents the term coming from the source term and prescribed initial conditions. Step 3:Apply the Adomian decomposition method,let the solution of the Eq.(5.1)series, and the nonlinear term can be decomposed as whereAnis called Adomian Polynomials ofu1,u2,u3,..,unand it can be calculated by the following formula: wheren=0,1,2,3,4,......... Substituting Eqs. (5.5)and(5.6)in the Eq. (5.4),we have Step 4:The recursive relation is given by, wheren=1,2,3,...andm=0,1,2,3,... At the end,we can approximate the dynamic analytical solution,as In this section,we do experiment and analyzed by both the proposed method. Example 6.1:Solve by Fractional conformable Sumudu transform decomposition method.Consider dynamic nonlinear non homogeneous partial fractional differential equation:Forα,β,γ∈(0,1],x,y,t∈[0,∞). with the initial conditions, Solution:Applying the conformable fractional triple Sumudu transform to both sides of Eq. (6.1) Recalling Lemma-4.1(i),we obtain, Using initial condition Eq. (6.2)and the inverse triple Sumudu transform,we obtain Applying the proposed method,we get the recursive formula, whereAnis the Adomian polynomial to decompose the nonlinear terms by using the relation; wheren=0,1,2,3,4,......... Let the nonlinear term can be represented as, Eqs. (6.6)-(6.8)gives, And so on... The approximate series solution is, forα,β,γ∈(0,1],x,y,t∈[0,∞). Note that forα,β,γ=1, the solution of Eq. (6.1)from Eq. (6.10),as which is exact solution of integer order of partial differential equation. Example 6.2:Solve by fractional conformable Laplace decomposition method. Consider nonlinear non homogeneous partial fractional differential equation, forα,β,γ ∈(0,1],x,y,t∈[0,∞). with initial conditions, Solution:Rewriting,Eq. (6.11)as: Imposing the fractional conformable triple Laplace transform to both sides, Recalling Theorem 3.4(4):Eq. (6.14)becomes, Using initial condition(6.12)and taking the inverse triple Laplace transform on Eq.(6.15),we obtain: Applying the proposed method,let And the recursive relation is, whereAnis the Adomian polynomial to decompose the nonlinear terms by using the relation; wheren=0,1,2,3,4,......... Let the nonlinear term be represented as, Note that,in Adomian relation,the linear term can be considered,in place of nonlinear.So,you may takef(u)=uand it leads to the same answer. So,this method is also valid for linear partial fractional differential equation. Forn=0, Therefore, Forn=1, Therefore, The approximate series solution is, Figure 1: 3D Plot of Eq. (6.20) for γ=0.50; β=0.25; y=1. Figure 2: 3D Plot of Eq. (6.20) for γ=0.75; β=0.50; y=1. forα,β,γ∈(0,1],x,y,t∈[0,∞). Note thatf or α,β,γ=1,the solution of Eq. (6.11)from Eq. (6.20)as, Figs. 1-4 show the 3D graphical representations for both the proposed methods, of Eq.(6.20)with various values ofβandγ. Figure 3: 3D Plot of Eq. (6.20) for γ=0.50; β=0.50; y=1. Figure 4: 3D Plot of Eq. (6.20) for γ=0.75; β=0.75; y=1. In this work, the definition of fractional conformable triple Laplace and Sumudu transform are defined and investigated using all our obtained novel results and theorems with its systematic proofs. The new fractional conformable triple Laplace and Sumudu transform decomposition methods are given in the generalized form, to find the solution of nonlinear partial fractional differential equations. Finally, a numerical experiment has been conducted using the proposed methods - conformable Sumudu and Laplace decomposition method,and analyzed it. Noted the outcome of both methods: Laplace and Sumudu transforms decomposition method yields the same results and mentioned with the graphical representation as fig. 1,2,3,4. which leads to the answer of question raised in[31].Infect,these methods can be led to solve simultaneous linear and nonlinear partial fractional differential equations. Acknowledgement We would like to thank the editors and the reviewers for their valuable comments on developing this paper and Dr Krunal B Kachhia,Faculty of Charusat University,Changa,Gujarat, India for his valuable suggestions and motivations for this research work: We also thank Prof Meghna Parikh,LJIET for their help developing the Tex file.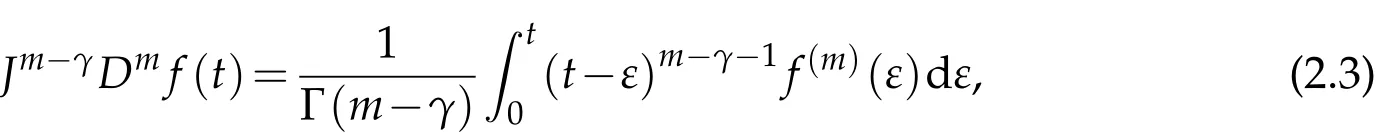



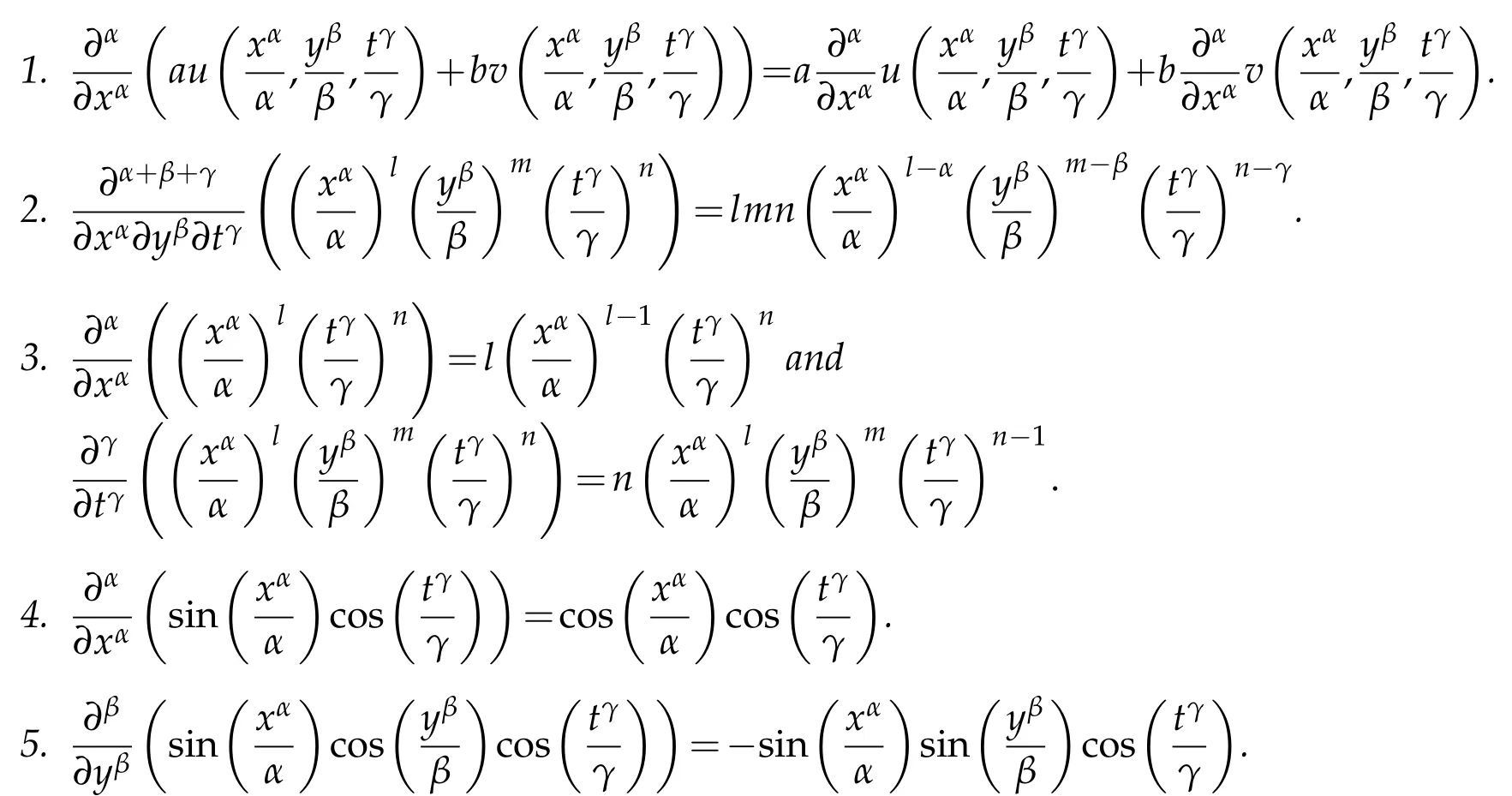
3 Some results and theorems of the conformable fractional triple Laplace transform




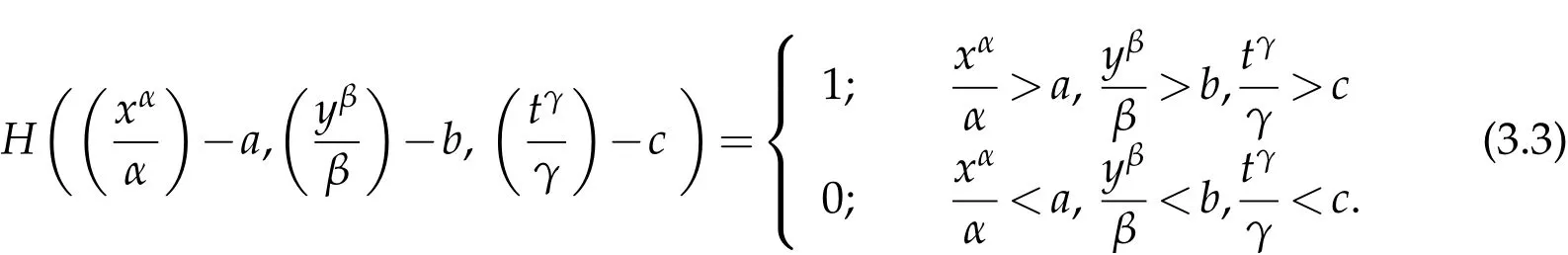












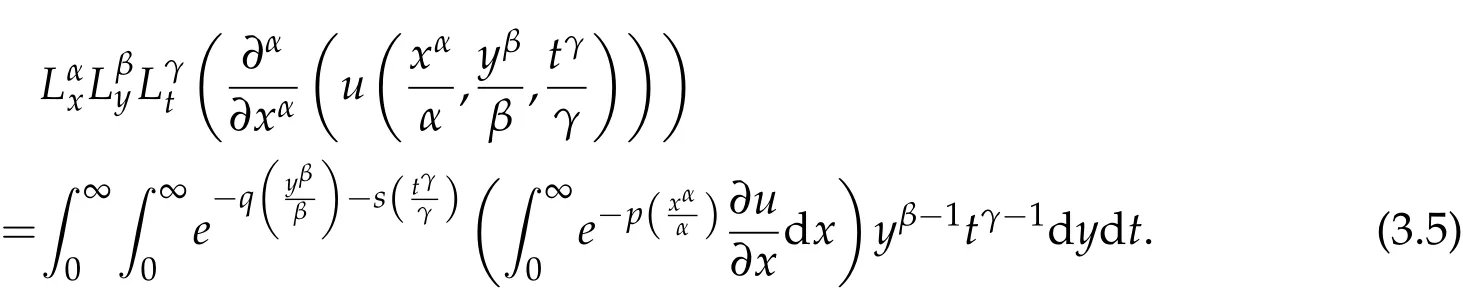

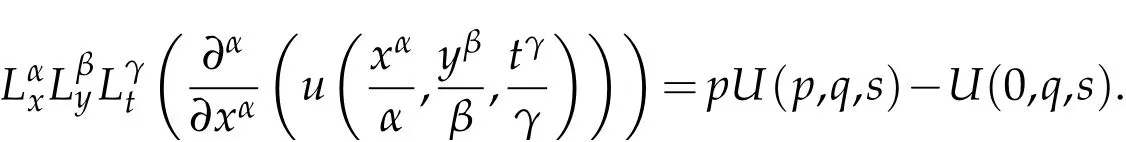

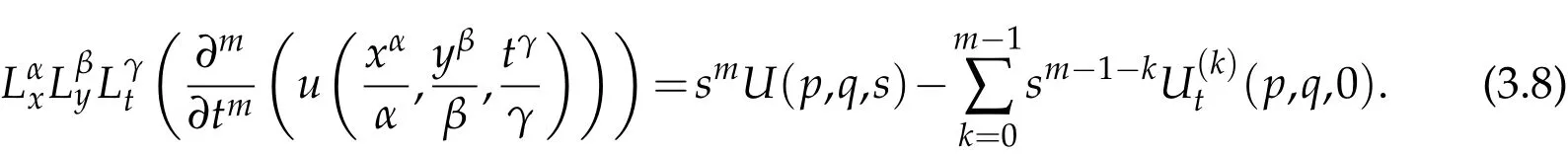
4 Some results and theorems of the fractional conformable triple Sumudu transform


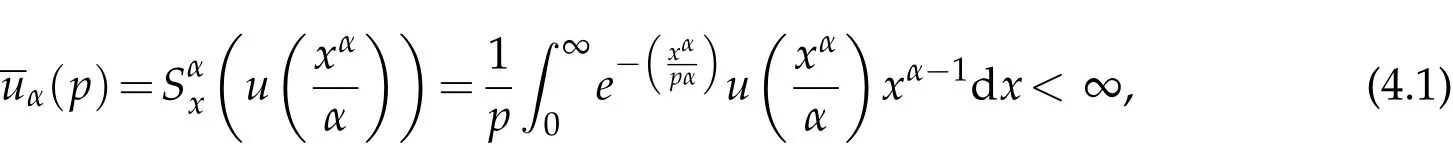






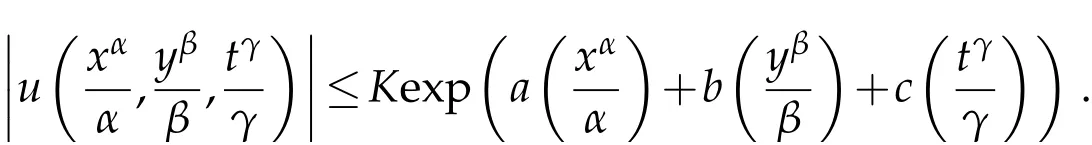
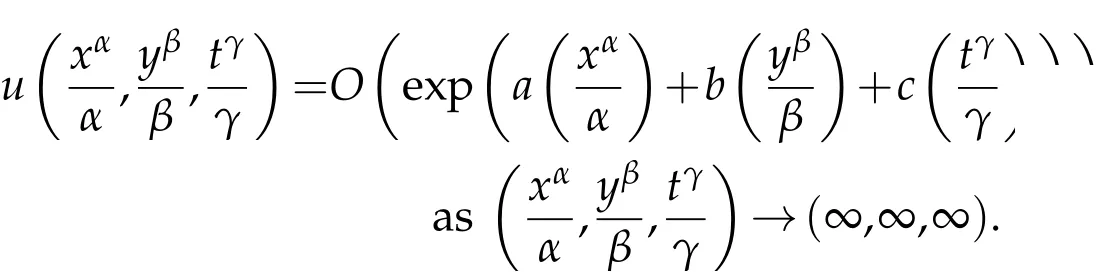



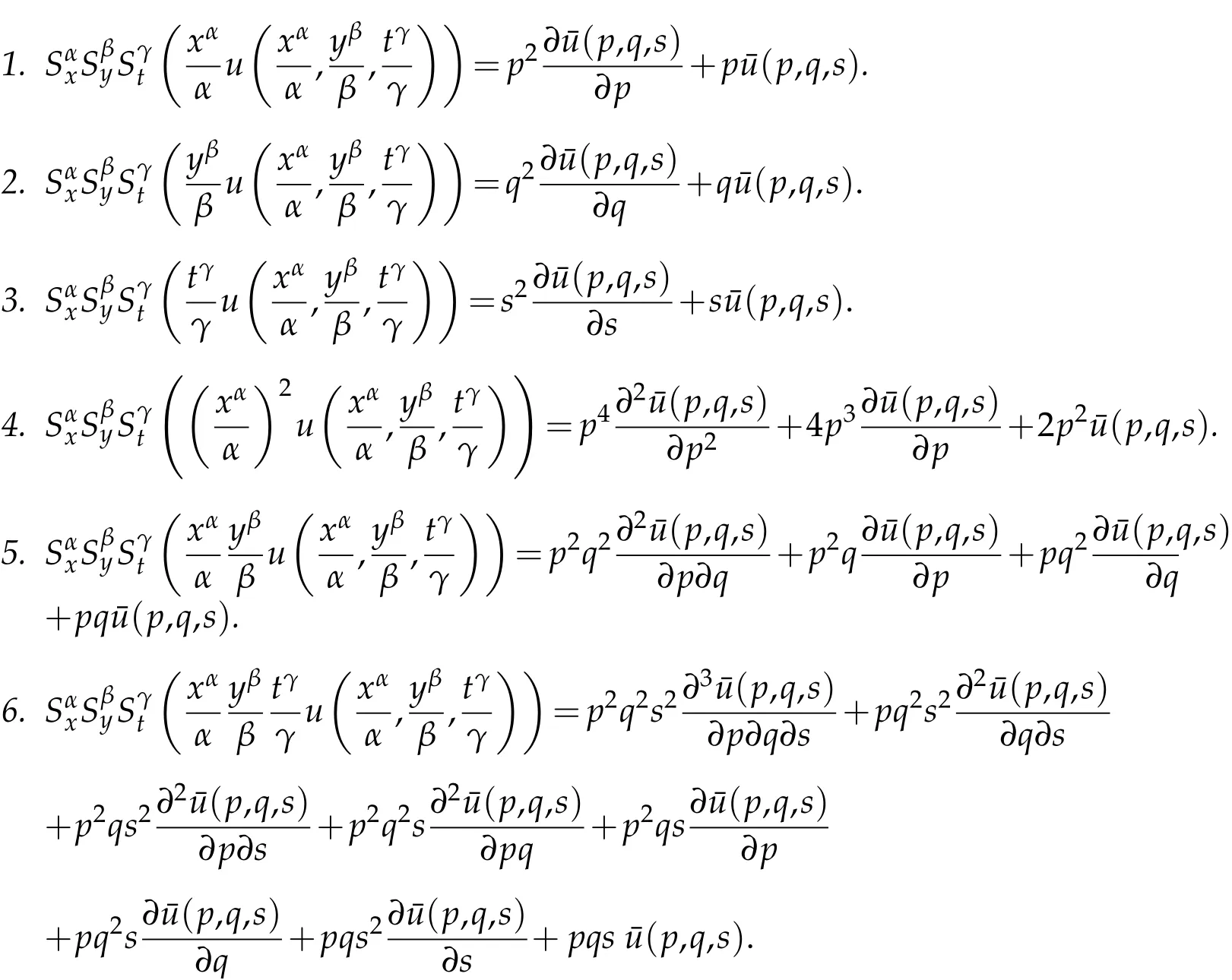
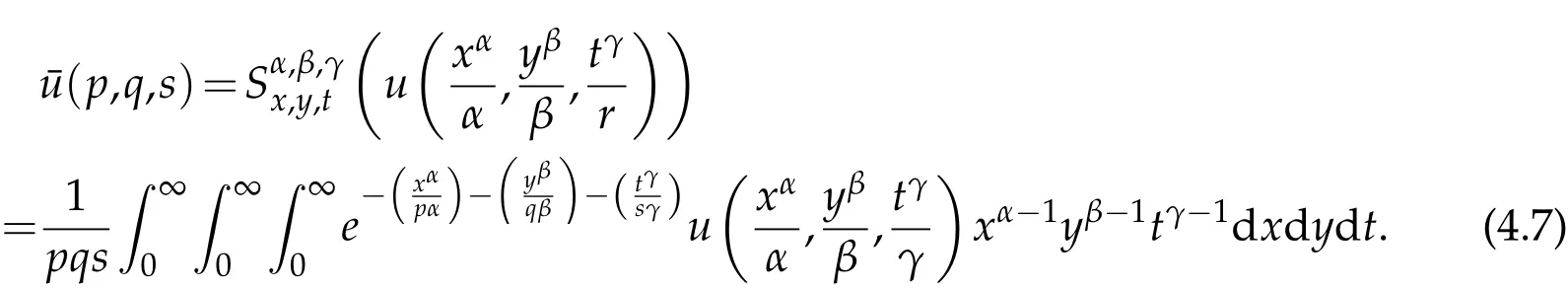



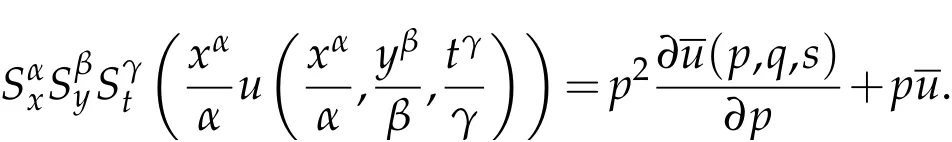


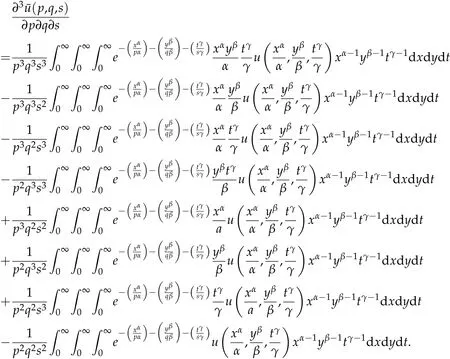
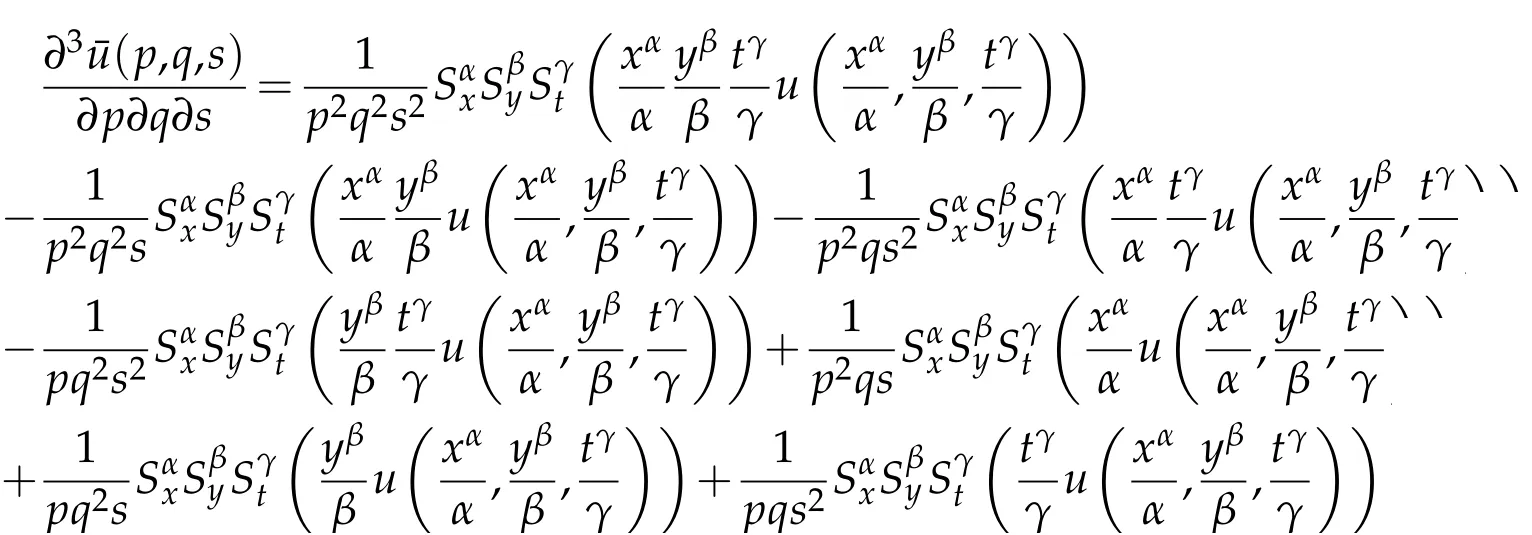





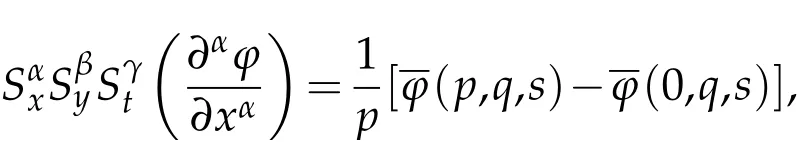





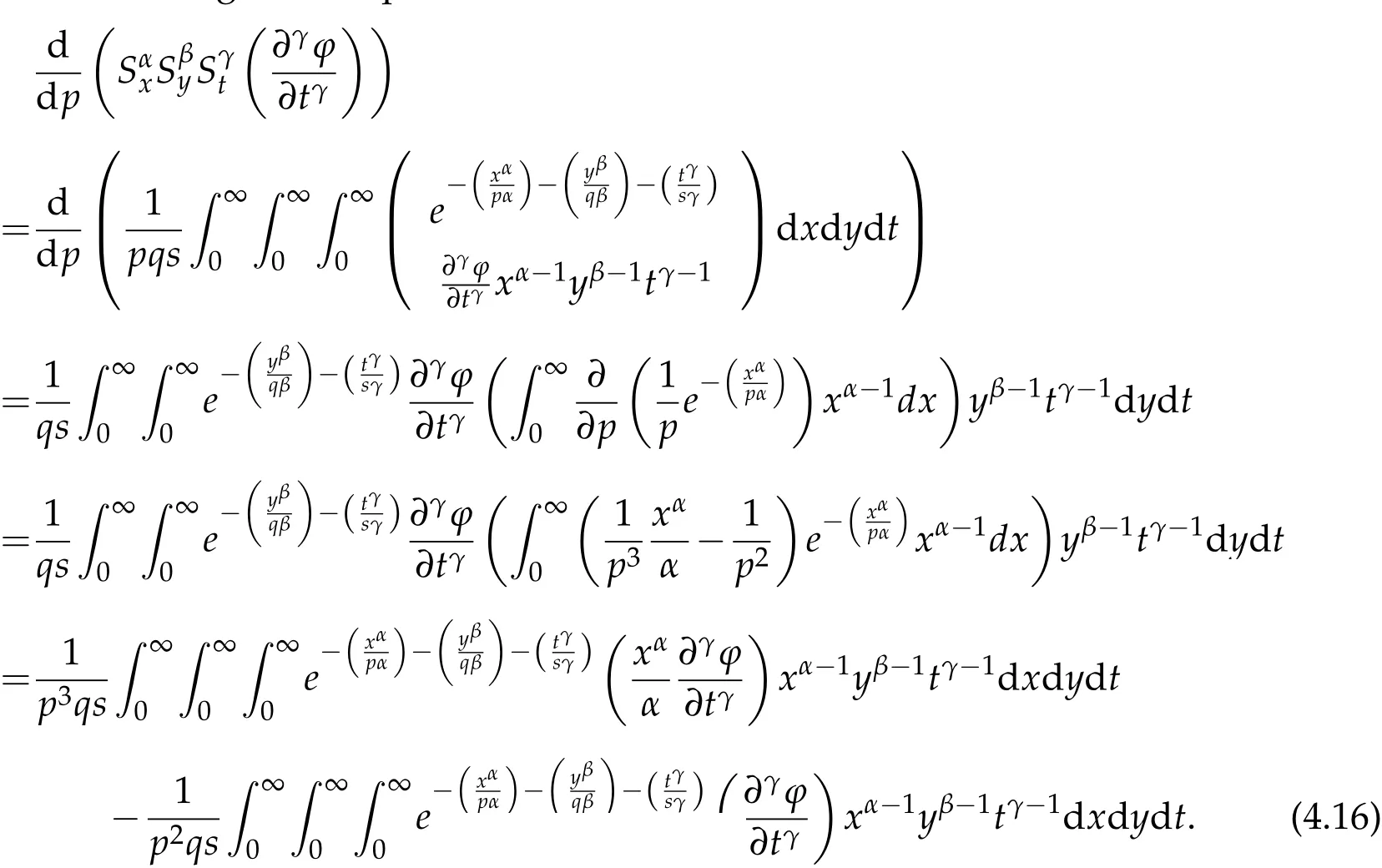
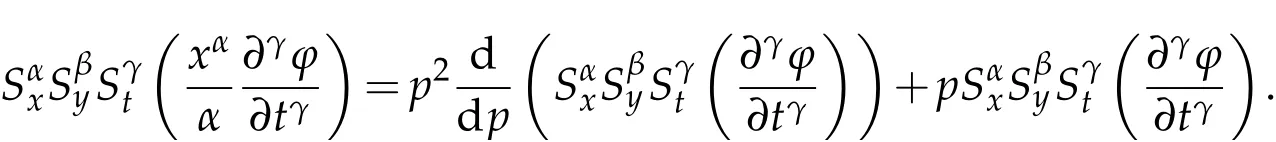

5 The fractional conformable triple Sumudu and Laplace transform and Adomian decomposition method



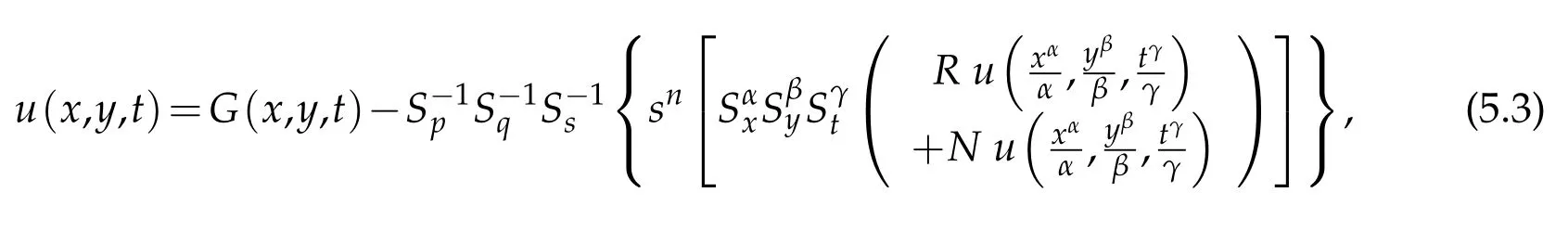

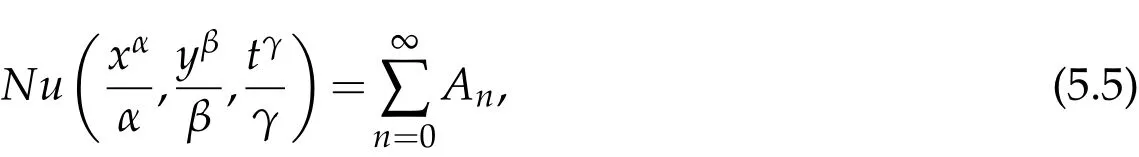
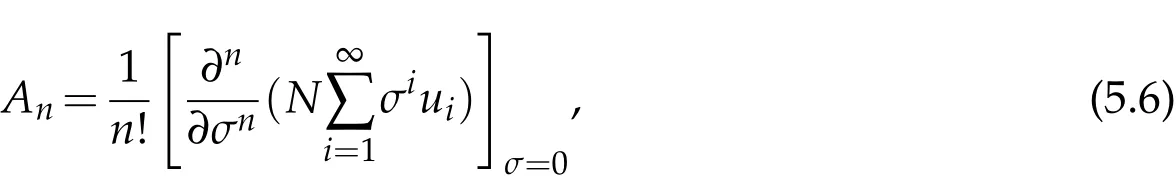



6 Applications


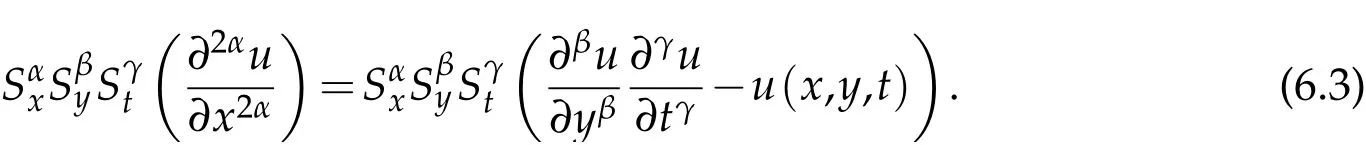


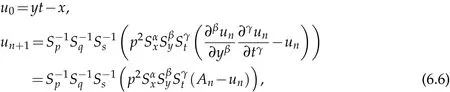


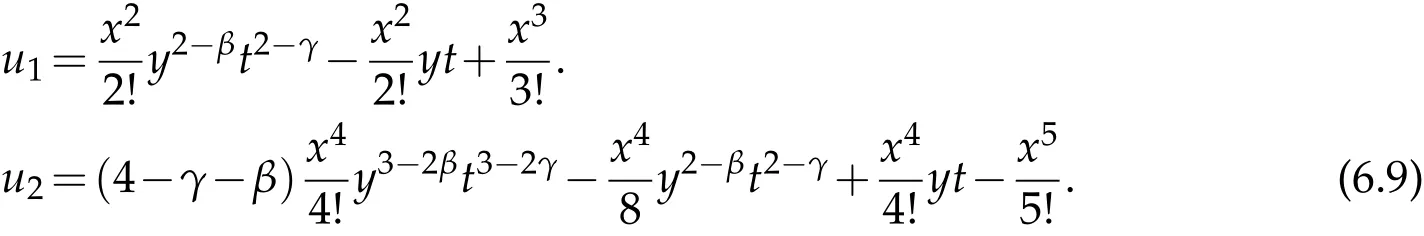


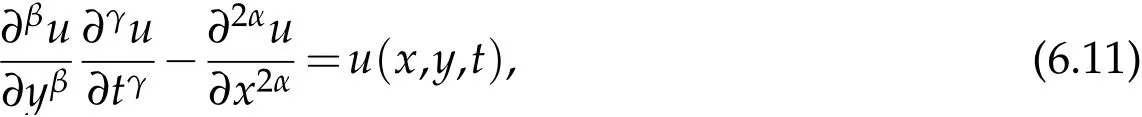
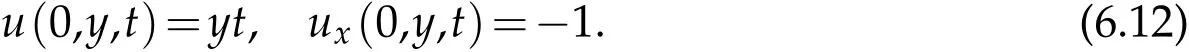






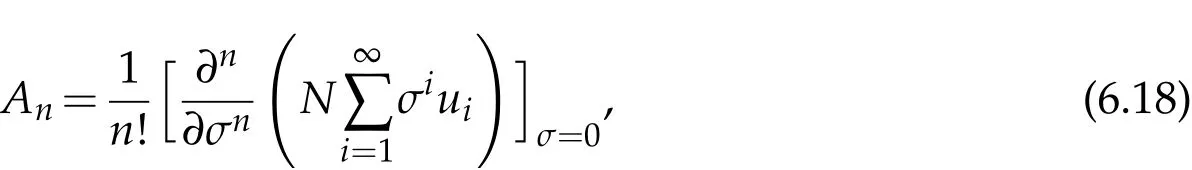





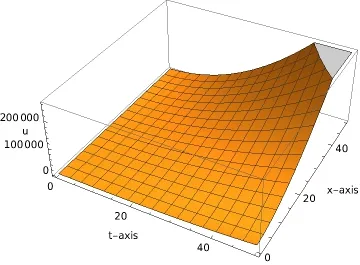
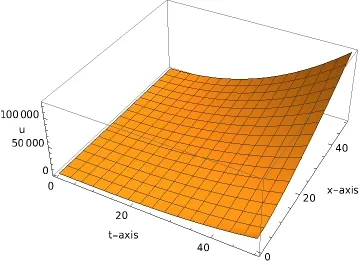

7 Conclusion


 Journal of Partial Differential Equations2022年1期
Journal of Partial Differential Equations2022年1期
- Journal of Partial Differential Equations的其它文章
- Implicit Finite Difference Scheme for Singularly Perturbed Burger-Huxley Equations
- Blow-up of Classical Solutions to the Isentropic Compressible Barotropic Navier-Stokes-Langevin-Korteweg Equations
- Integrated Pest Management System with Impulsive Control of Spatial Heterogeneity
- Gelfand-Shilov Smoothing Effect for the Radially Symmetric Spatially Homogeneous Landau Equation under the Hard Potential γ=2
- An Averaging Principle for Caputo Fractional Stochastic Differential Equations with Compensated Poisson Random Measure
