架空配电线路雷电感应电压特性及解析算法性能分析

于建立 张迎栋程 龙鲁志伟

(1.潍坊学院机械与自动化学院,山东潍坊 261061;2.现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林吉林 132012;3.武汉大学电气与自动化学院,湖北武汉 430072)

1 引言

雷电一直是导致架空线路故障的重要因素,其危害方式包括直击雷和雷电感应电压[1-2].雷电感应电压对架空线路的威胁主要存在于35 kV及以下的配电线路,110 kV及以上的输电线路因绝缘水平较高而很少由其造成事故[2].地闪回击电磁场具有多样化的耦合路径且传播范围极广,保障架空配电线路安全运行的关键问题之一,即是雷电感应电压的防护.

雷电感应电压的准确计算和特性的深入理解是对其进行可靠防护的前提.架空线雷电感应电压的计算方法可分为解析算法和数值算法两类:前者基于静电理论认为束缚电荷的运动产生过电压并以回击电流幅值、导线高度和落雷距离3个特征量为输入参数总结出相应的计算公式[3-6];后者基于电磁理论认为回击电磁场的激励作用在导线上产生过电压[7-9].二者的计算对象分别为导线上距雷击点最近位置的雷电感应电压幅值和观测点位置的雷电感应电压时域波形.Rusck等于1958年通过引入回击速度的影响对解析算法进行改进,改进算法虽于2011年被IEEE标准所采用但认为其存在较大的计算误差[10].解析计算公式由于表达简单易实现的优点多被电力运行部门应用于架空线路雷电感应电压的估算[3].但由于其计算准确性较差且仅能估算电压幅值而无法进行更多研究性分析并不被研究人员所关注.自上世纪60年代以来雷电感应电压的数值计算方法经过众多研究人员的开发与改进现已较为成熟[11].基于不同的计算模型国内外学者在雷电感应电压特性分析及防护等方面开展了一系列研究工作.张其林等采用三维时域有限差分(3-D finite-different time-domain,3-D FDTD)法计算了土壤垂直分层情况下的架空线雷电感应电压,该工作为进一步理解土壤电特性对感应电压的影响提供了参考[12].Thang等采用FDTD方法仿真计算了带有避雷器和变压器的架空线雷电感应电压,并将计算结果与试验数据进行对比[13].刘欣等基于Agrawal耦合模型将分布式激励源进行集中等效提出了计算雷电感应电压的宏模型,并结合蒙特卡罗法计算了10 kV架空线路的跳闸率[14].Cooray等通过标量势和矢量势的引入对Rusck场线耦合模型进行了改进[15].Barbosa等提出了考虑地闪回击速度的闭合回路导体中雷电感应电压的计算公式[16].Andreotti等采用电路法计算了考虑回击通道弯曲度的较复杂电力系统的雷电感应电压[17].

目前,架空线雷电感应电压在特性研究方面还不够系统和全面.此外,根据实际的工程需求可知,并非所有情况下都需要获取雷电感应电压的时域波形,若能通过解析计算较为准确的掌握其幅值对于工程应用亦有较高的实用价值[18].研究人员虽通过各种途径证实了解析计算的不准确性,但并未对解析算法的计算精度进行定量化的分析.基于目前的研究现状,本文采用二阶FDTD和Agrawal耦合模型相结合的数值计算方法对架空配电线路雷电感应电压进行计算[19].以解析计算公式中3个特征参数为考察对象对雷电感应电压特性进行研究,在此基础上对解析算法的计算误差进行定量化分析.本文工作进一步揭示了架空线路电磁耦合的物理机制,加深了对雷电感应电压特性的理解.此外,在实现对解析算法计算性能系统性评价的基础上,可为配电网运维部门在架空线路安全性评估和雷电防护装置的优化配置方面提供理论指导.

2 计算方法

架空线雷电感应电压的计算方法可以概括为基于静电理论的解析计算方法和基于电磁理论的数值计算方法.

2.1 解析计算方法

雷电感应电压静电分量的物理基础是导线中束缚电荷的运动.当落雷点与架空线之间的落雷距离S ＞65 m时,基于静电理论的导线雷电感应电压解析计算方法如式(1)所示[3-6]:

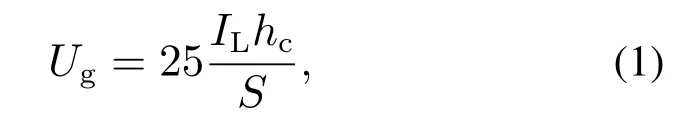
式中:Ug为导线上距落雷点最近处的雷电感应电压幅值(kV),IL为回击电流幅值(kA),hc为导线架设高度(m),S为落雷距离(落雷点与导线间的地面垂直距离,m).由式(1)可知,若分别保持其他参数值不变,则Ug与IL和hc均成正比,与S成反比.

需要注意的是,由于本文的计算对象为架空配电线路且电压等级较低(针对10 kV线路),通常不会架设避雷线,因此本文只介绍没有避雷线情况下的架空线雷电感应电压计算.

2.2 数值计算方法

目前常用的架空线雷电感应电压数值计算方法一般由2个计算环节构成:

1) 将地闪回击电流作为激励源,采用解析方法或数值方法计算获取回击通道周围空间的电磁场;

2) 以步骤1)中计算所得地闪回击电磁场作为激励源,采用数值方法求解电磁场与架空导线的耦合电路方程,进而获取导线上各点的雷电感应电压和感应电流时域波形.

本文采用文献[19]所介绍的数值计算方法对架空线雷电感应电压进行计算.在该方法中采用FDTD实现计算环节1)中地闪回击电磁场的计算,然后采用二阶FDTD法求解Agrawal耦合模型的电路方程,获取观测点雷电感应电压波形.在地闪回击电磁场的计算中,本文采用一个Heidler函数和一个双指数函数叠加拟合回击基电流[20]:

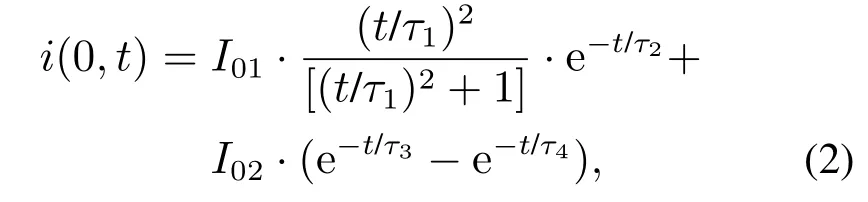
式中:I01和I02决定回击电流的幅值,τ1和τ4决定回击电流的上升时间,τ2和τ3决定回击电流的下降时间.另外,鉴于工程回击模型具有显著的表达简单易实现且计算所得电磁场与几十米乃至几十千米范围内观测结果吻合度较高等优点,本文采用其中的改进线性衰减传输线(modified transmission-line model with linear current decay with height,MTLL)模型[21]:

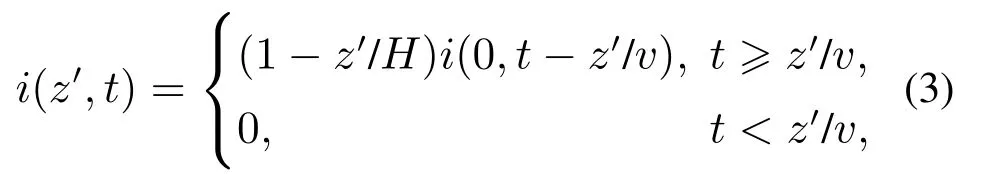
式中:z′为回击通道内任一点高度,t为时间,i(z′,t)表示t时刻通道内z′高处电流,v为回击速度,H为回击通道高度.

考虑大地影响的Agrawal耦合模型多导线控制方程为[8]

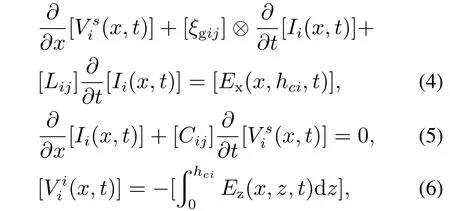
式(4)-(6)中:i,j为导线序号;x,z分别表示沿导线方向和垂直导线方向;hc为导线高度;V s,V i和I为节点的散射电压、入射电压和全电流;Ex和Ez分别为2个方向的入射电场;L和C分别为导线单位长度的电感和电容;ξg为大地瞬态阻抗;⊗表示卷积积分.

由于本文所用雷电感应电压数值计算方法为成熟方法,本文旨在以该方法为工具探索架空配电线路雷电感应电压特性,有关该计算方法的详细实现过程不再赘述.

图1所示为架空线雷电感应电压数值计算与现场实测的对比结果.试验布置参数为:水平架空线长度1300 m,高度3 m,观测点位于距线路一端5 m处,落雷点距导线约400 m且距导线两端距离相等,回击电流幅值为20 kA.

图1 实测和数值模拟雷电感应电压Fig.1 Measured and numerically simulated lightning induced voltage

3 数值计算及分析

本文通过定量分析解析计算方法式(1)中各参数(hc,IL和S)的影响,对架空线感应电压特性进行深入研究,以此对解析计算方法的有效性进行评估,并对其后续的改进提出建议.

以10 kV架空配电线路为研究对象,杆塔结构和尺寸参数均参考国家电网公司《配电网工程典型设计-10 kV架空导线分册》进行设置.单(双)回路塔头结构及参数如图2所示,图2(a)中单回路三相导线架设高度为10 m,图2(b)中双回路上下两回导线架设高度分别为12.7 m和11.6 m.

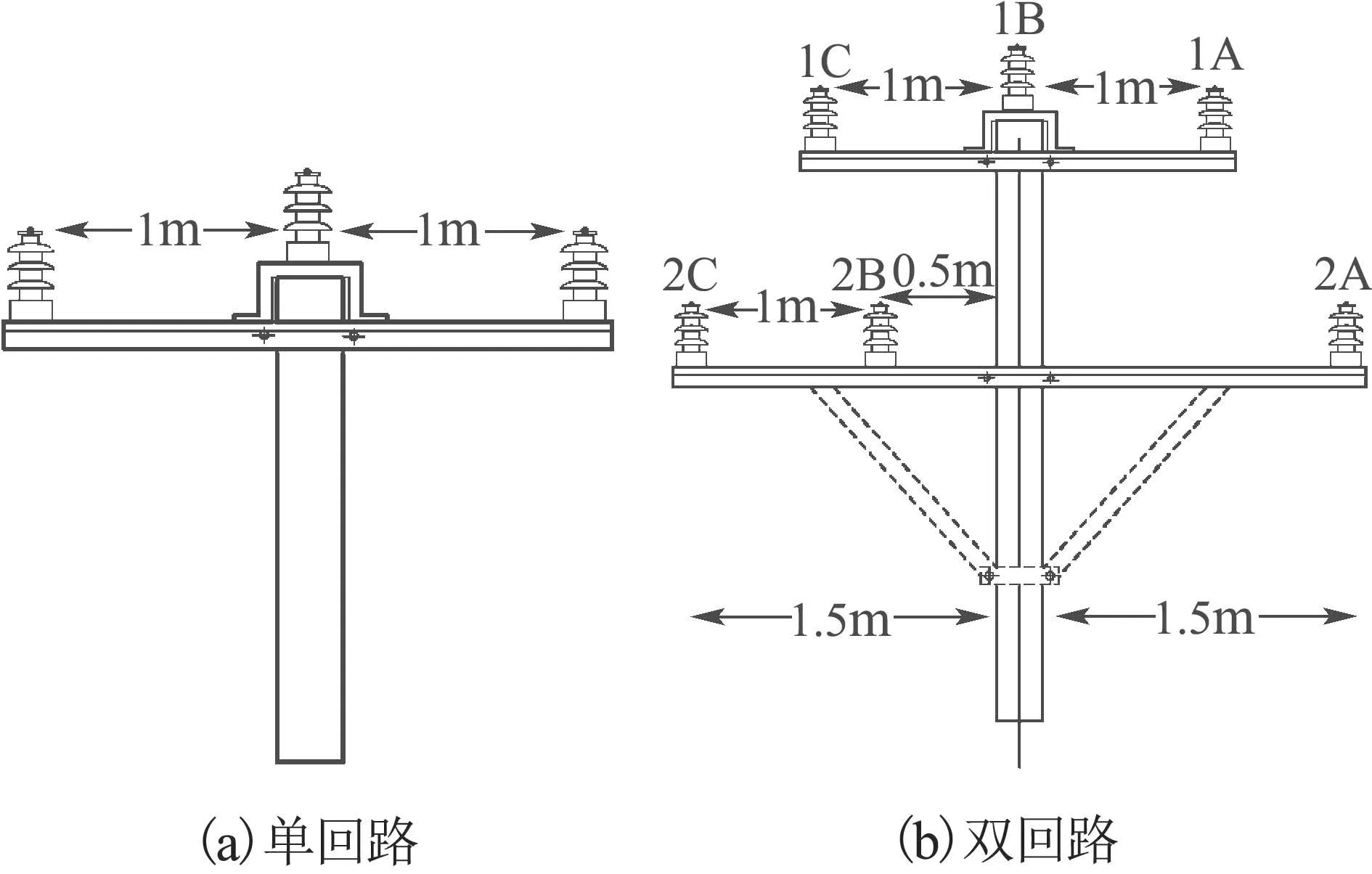
图2 单(双)回线路塔头结构Fig.2 Structure of single(double)circuit tower head

需要说明的是,由于实际运行线路的架设高度均有明确规定而无法考察其影响.在分析高度因素的影响时,为得到更直观的效果并排除其他因素的干扰,计算对象设置为双端匹配接地的架空单导线.

3.1 导线架设高度的影响

根据式(1),若回击电流幅值和落雷距离确定,则架空线雷电感应电压幅值应与导线对地高度成正比.本文对导线高度分别取4 m,8 m,12 m,16 m和20 m时的感应电压进行计算.落雷点与导线两端距离相等,导线长度、导线与落雷点相对位置以及导线上观测点(共13个点)设置如图3所示.

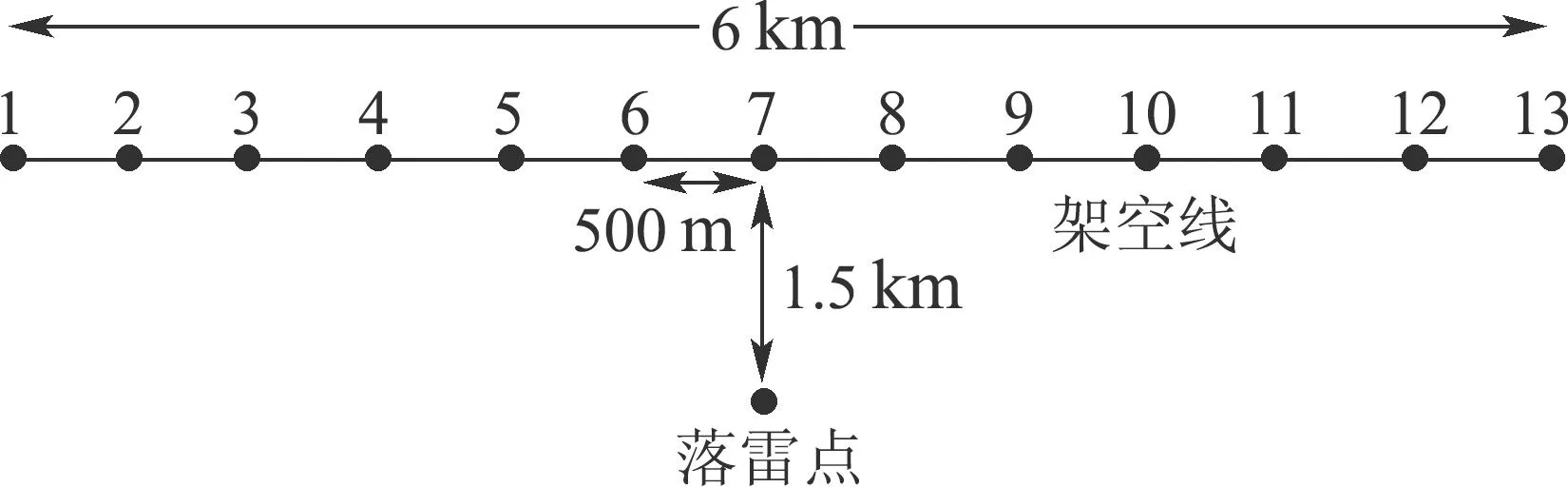
图3 线路观测点设置Fig.3 Observation points setting on lines

该部分计算采用式(2)的回击电流波形和式(3)的回击模型,式中各计算参数取值为:I01=2.6 kA,I02=8.0 kA,τ1=0.072µs,τ2=16.67µs,τ3=100µs,τ4=0.5µs,H=7 km,v=1.5×108m/s,此 外,大地电导率σ=2×10−3S/m,大地相对介电常数ε=10.图4给出了3,7,11共3个观测点(限于论文篇幅未给出所有观测点计算结果)的雷电感应电压波形.若不考虑脉冲极性,图5给出了3个观测点雷电感应电压脉冲幅值以及采用式(1)计算雷电感应电压随导线高度的变化情况.

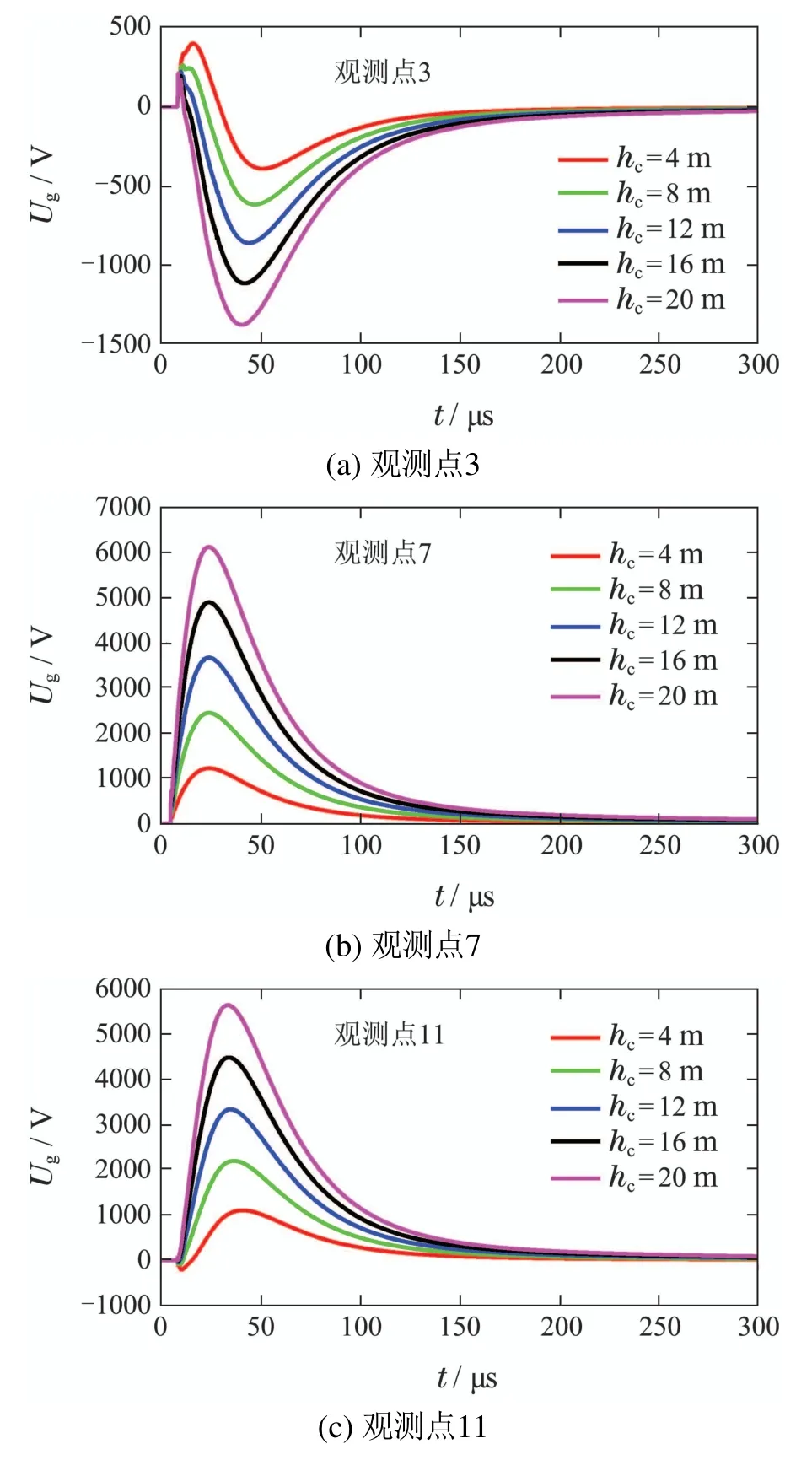
图4 不同导线高度时雷电感应电压波形Fig.4 Lightning induced voltage waveforms for different conductor heights

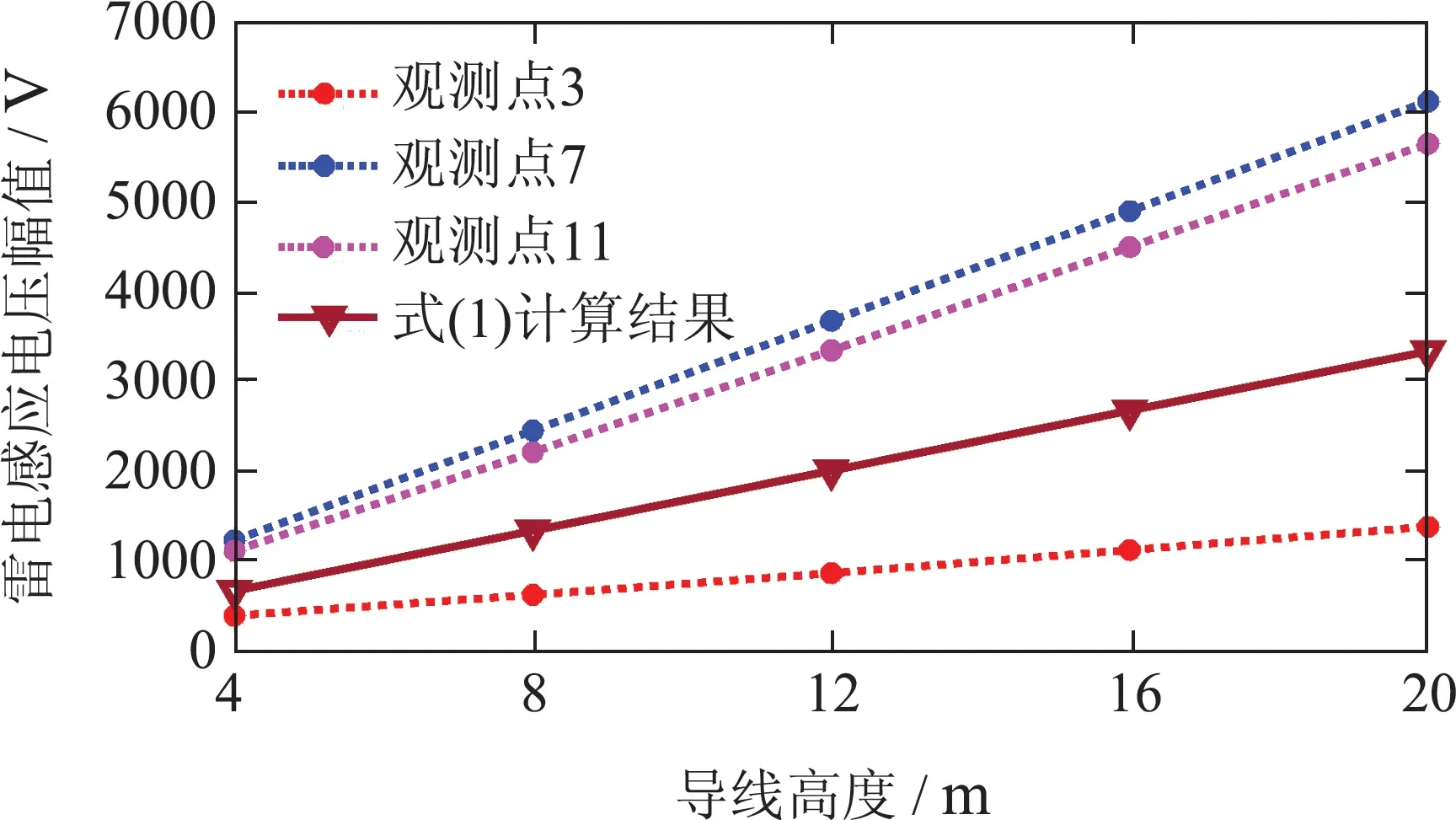
图5 雷电感应电压幅值随导线高度的变化Fig.5 Variation of lightning induced voltage amplitude with conductor height

图4中,当观测点雷电感应电压出现双极性脉冲时,定义幅值较高者为“主脉冲”,幅值较低者为“次脉冲”,若非特殊说明本文讨论脉冲幅值的对象默认为“主脉冲”.观测点3与其他观测点的电压脉冲极性相反,这是由于在水平电场的激励下导线中的电荷定向运动,在导线与大地组成的回路中形成电流,从而使导线两端积累异极性电荷所致.由图4可见,导线高度对雷电感应电压的影响主要体现在电压脉冲幅值和脉冲上升陡度,二者均随导线架设高度的增大而明显提高,且幅值影响效果尤为明显.其中,感应电压脉冲幅值提高是由于地闪回击水平电场的场强在地面以上几十米以内的高度范围内随高度增加而增强[22].本文采用Agrawal耦合模型进行感应电压计算,在该模型中水平电场是最主要的激励源,因此导线上感应电压激励源的“作用强度”必然随导线高度增加而增强.

另一方面,可以借助法拉第电磁感应定律对该现象进行理解,根据法拉第电磁感应定律可知

式中:Ug为导线上的感应电压,φ表示穿过“闭合面”的磁通,t为时间,其中dφ=B·dSm,B为“闭合面”内的磁场强度,Sm为“闭合面”的面积.导线高度增加可理解为导线与地面构成的闭合回路面积增大,则单位时间内穿过该“闭合面”的磁通量将增加,亦即感应电压将提高.

由图5可见,采用数值计算方法与采用式(1)计算所得雷电感应电压幅值均随导线高度增大而近似线性提高,这说明式(1)中雷电感应电压幅值与导线高度成正比关系是基本合理的.由于式(1)的计算对象应为观测点7[3-6],可见其计算结果明显偏低,存在较大误差.

以式(1)计算对象(观测点7)做对比,以本文数值计算结果为标准,图6(a)和图6(b)分别为式(1)计算结果与标准值之间的幅值差(ΔUg)和幅值的相对误差(δh).由图6可见,式(1)在本文工况参数下其计算所得雷电感应电压幅值偏低可达约500 V至2700 V,ΔUg随导线高度增加而近似线性增大,不同导线高度时的δh均超过45%.

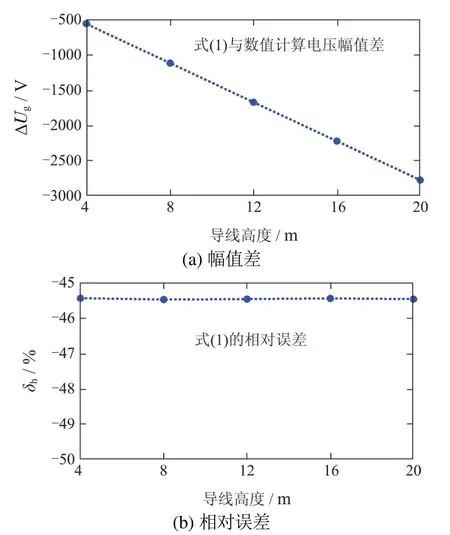
图6 导线高度对式(1)计算误差的影响Fig.6 Influence of conductor height on calculation error of formula(1)

由上述分析可知,导线高度与雷电感应电压幅值成线性关系,式(1)计算所产生幅值差和相对误差亦与导线高度基本成线性关系.

3.2 回击电流幅值的影响

根据式(1),若导线架设高度和落雷距离确定,则架空线雷电感应电压幅值应与回击电流幅值IL成正比.根据此前研究人员采用地闪定位系统观测所得统计数据表明,幅值为10～30 kA的地闪占有明显较高的比重[23-24].为考察回击电流幅值对架空线雷电感应电压的影响.本文在计算中设定回击电流幅值的取值范围为10～30 kA(以5 kA为变化步长).以图2(a)中A相导线和图2(b)中1A相导线为计算对象,观测点位置分布及落雷点如图3所示.图7和图8分别给出了不同回击电流幅值时,单/双回路架空配电线路中3个观测点(3,7,11)的雷电感应电压计算结果.图9给出了3个观测点雷电感应电压脉冲幅值以及采用式(1)计算雷电感应电压随回击电流幅值的变化情况.

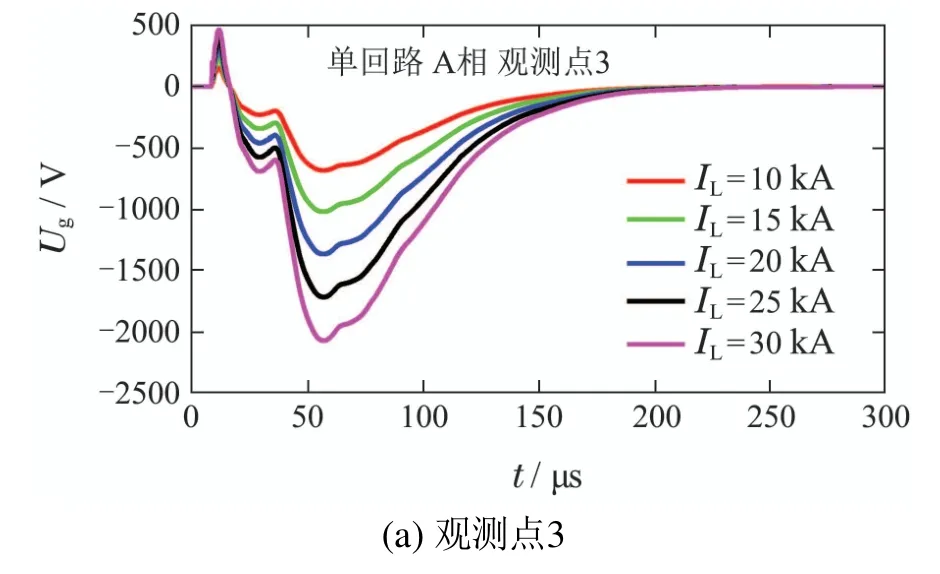
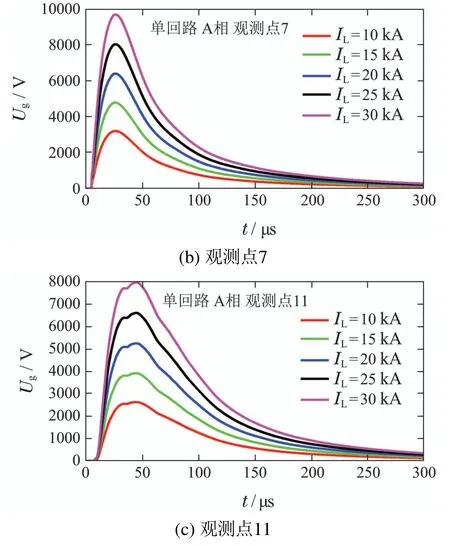
图7 不同回击电流幅值时单回线路雷电感应电压波形Fig.7 Lightning induced voltage waveforms of single circuit for different return-stroke current amplitudes

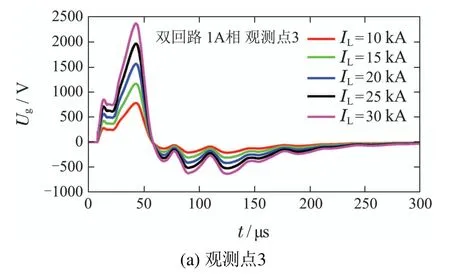
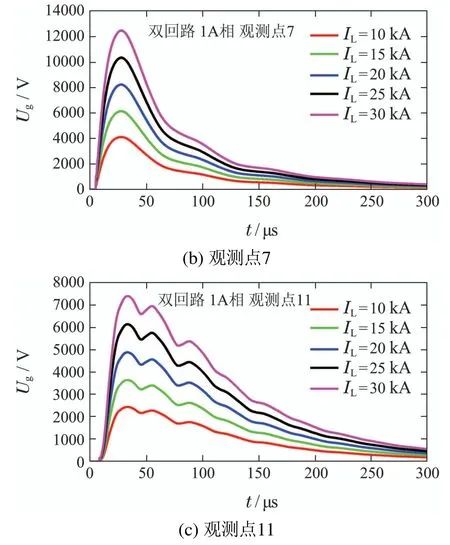
图8 不同回击电流幅值时双回线路雷电感应电压波形Fig.8 Lightning induced voltage waveforms of double circuit for different return-stroke current amplitudes

由图7-8可见,回击电流幅值对架空线雷电感应电压计算结果的影响几乎仅体现在脉冲幅值.由图9可见各观测点数值计算结果和采用式(1)计算所得雷电感应电压幅值均随回击电流幅值增大而线性提高,这说明式(1)中雷电感应电压幅值与回击电流幅值成正比关系是合理的.

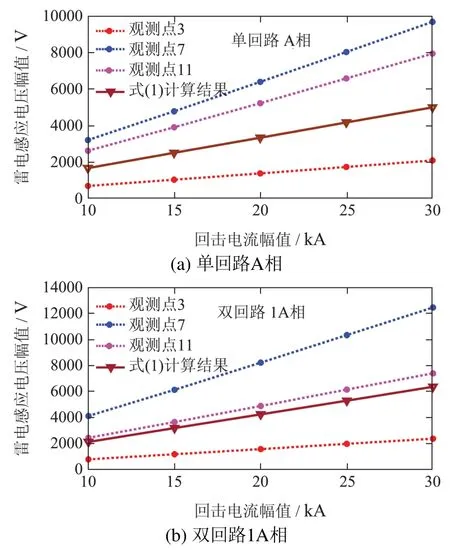
图9 雷电感应电压幅值随回击电流幅值的变化Fig.9 Variation of lightning induced voltage amplitude with return-stroke current amplitude

同样以式(1)计算对象(观测点7)为对比对象,若以本文数值计算结果为标准,图10(a)和图10(b)分别给出了式(1)计算结果与标准值之间的幅值差(ΔUg)和幅值的相对误差(δI).由图10(a)可见,式(1)计算结果明显偏低,单/双回路计算ΔUg分别偏低约1500～4700 V和2000～6000 V,ΔUg随回击电流幅值增大近似线性增加.由图10(b)可见,应用式(1)计算单/双回路所产生的δI高达48%～49%,且该误差在IL=15 kA时最低,在15 kA ≤IL≤30 kA时随回击电流幅值增大而近似线性增加.

此外,由图10可知采用式(1)计算双回路感应电压幅值所产生误差明显高于单回路,这是由于在雷电感应电压的计算中平行多导线之间互相影响的媒介条件为互电感和互电容,导线数越多导线间的互电感和互电容越多,多导线相互间的影响会越复杂,故此该影响随导线数增多而增大.式(1)的应用没有考虑该影响,其计算误差必然随导线数增多而增大.

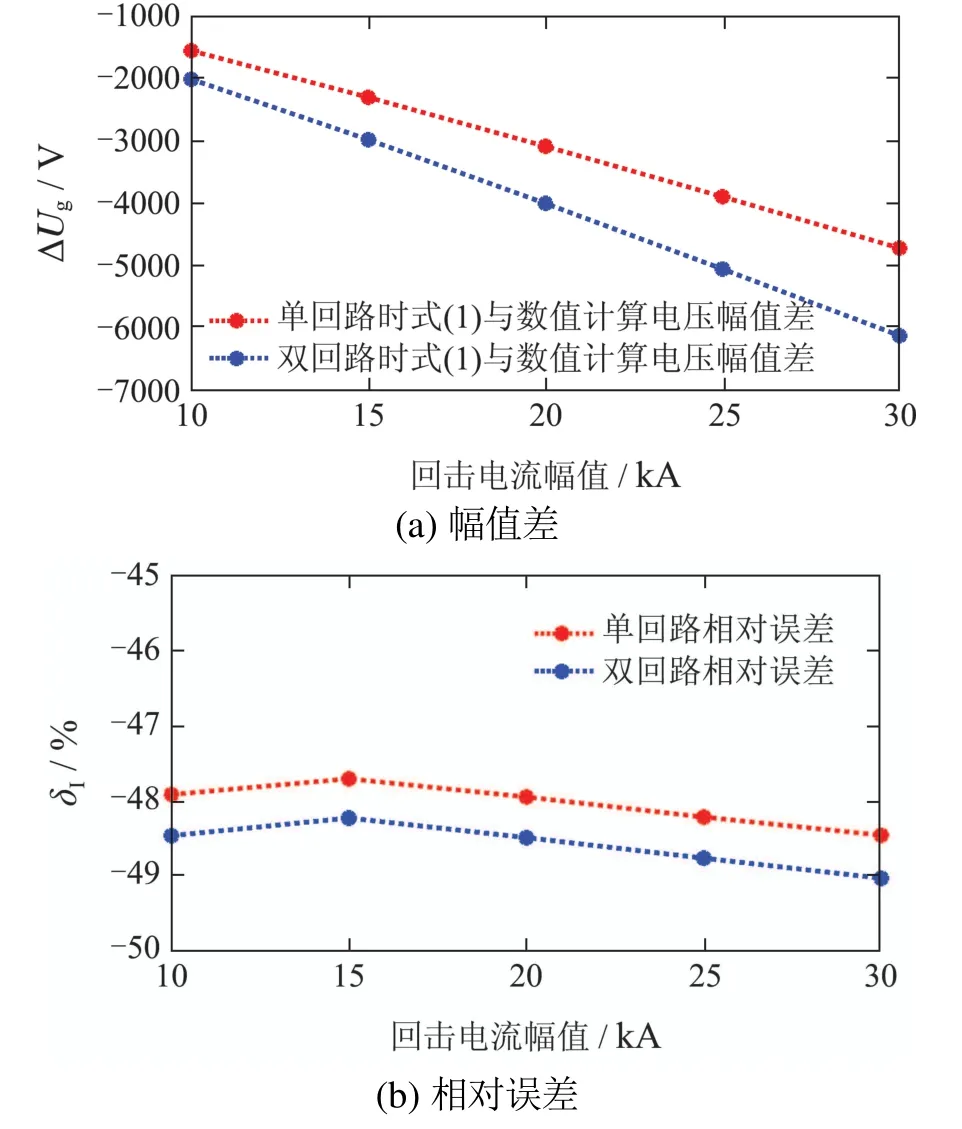
图10 回击电流幅值对式(1)计算误差的影响Fig.10 Influence of return-stroke current amplitude on calculation error of formula(1)

由上述分析可知,回击电流幅值与雷电感应电压幅值成线性关系.式(1)计算的ΔUg与回击电流幅值近似成线性关系,式(1)计算的δI与回击电流幅值整体为非线性关系,但在15 kA ≤IL≤30 kA时二者近似为线性关系.

3.3 落雷距离的影响

由式(1),若导线架设高度和回击电流幅值确定,则架空线雷电感应电压幅值应与落雷距离成反比.为考察落雷距离对架空线雷电感应电压的影响,本文取落雷距离为0.5～2.5 km(以0.5 km为递增步长),落雷点始终与线路两端距离相等.以图2(a)中A相导线和图2(b)中1A相导线为计算对象,观测点位置分布如图3所示,回击电流幅值取10 kA.图11和图12分别给出了不同落雷距离时,单/双回路架空配电线路中3个观测点(3,7,11)的雷电感应电压计算结果.图13给出了3个观测点雷电感应电压脉冲幅值以及采用式(1)计算雷电感应电压随落雷距离的变化情况.

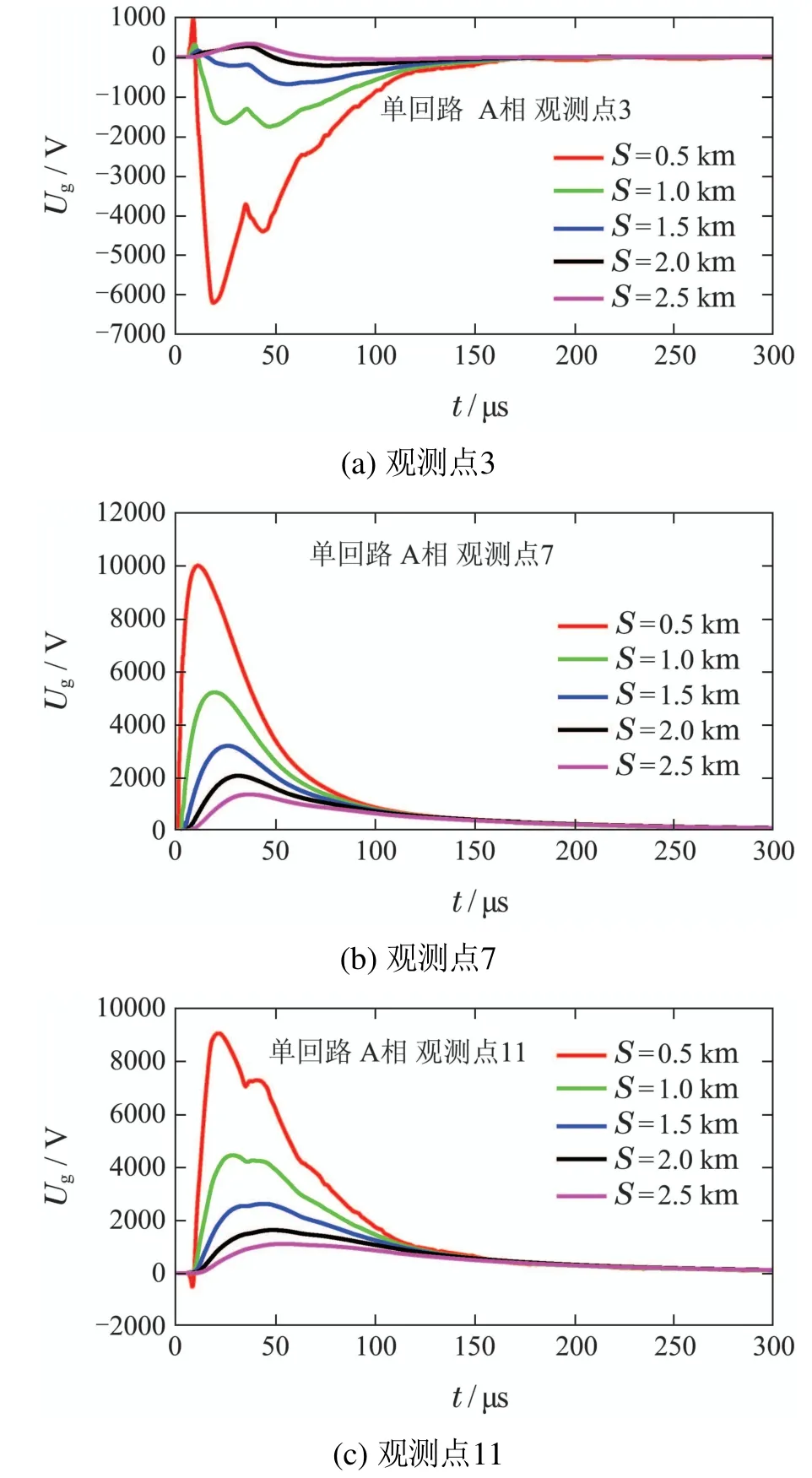
图11 不同落雷距离时单回线路雷电感应电压波形Fig.11 Lightning induced voltage waveforms of single circuit for different return-stroke distances

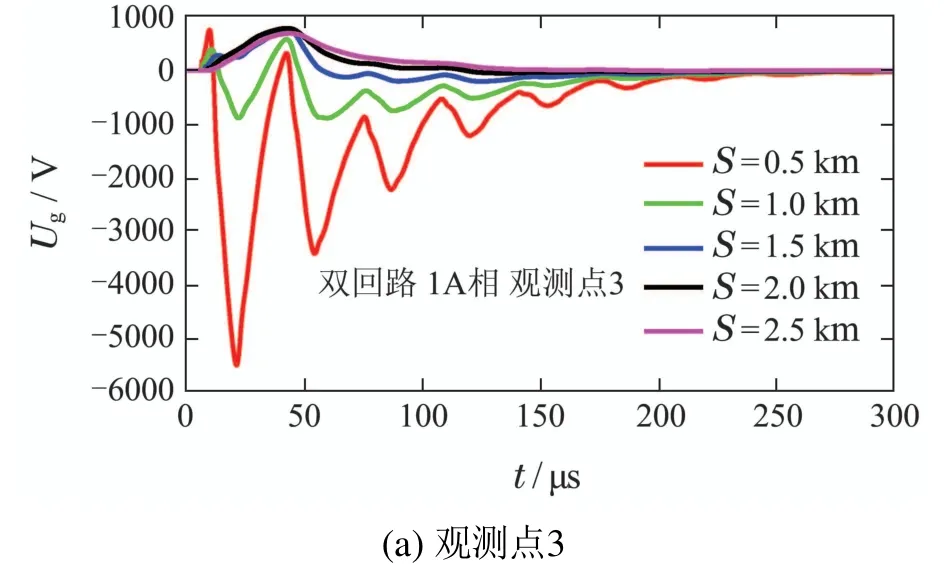
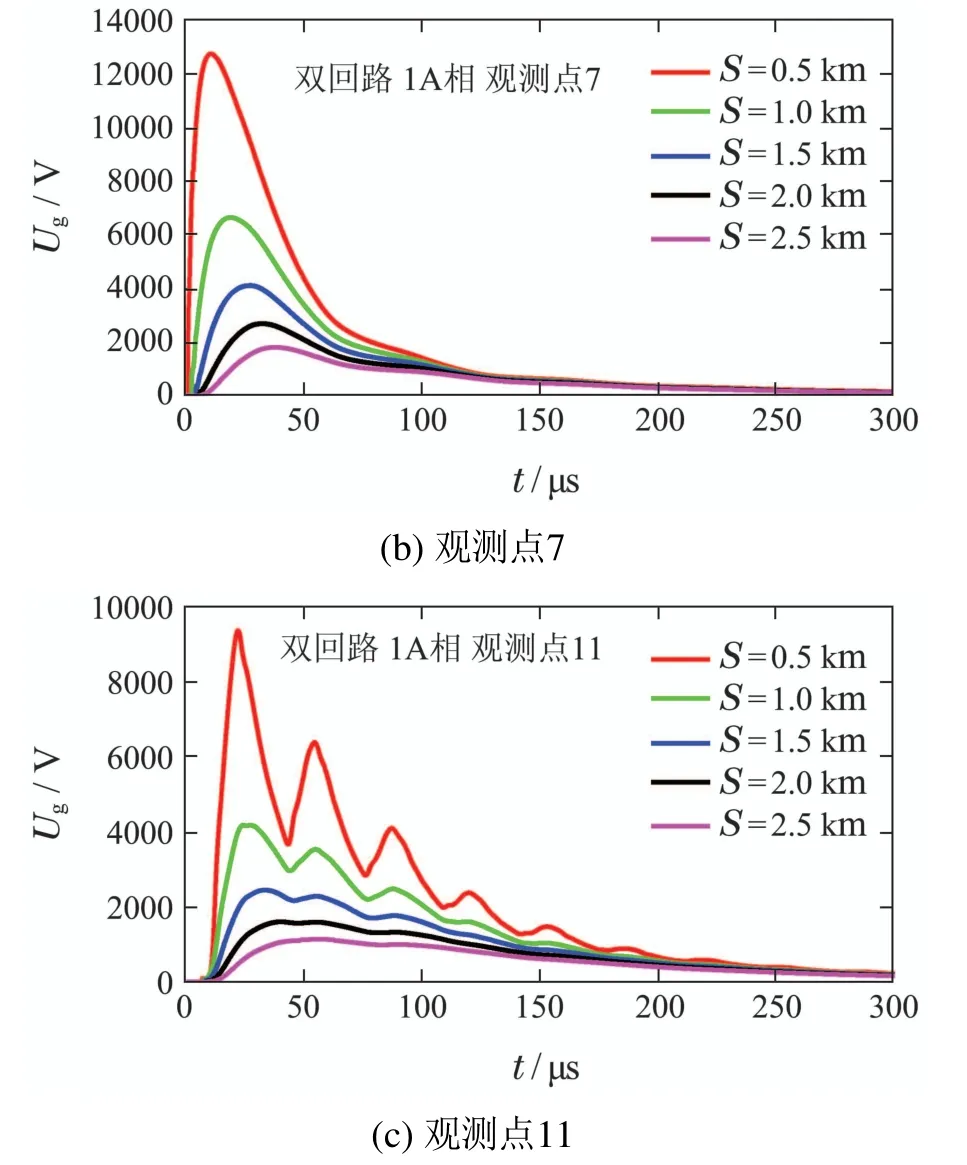
图12 不同落雷距离时双回线路雷电感应电压波形Fig.12 Lightning induced voltage waveforms of double circuit for different return-stroke distances

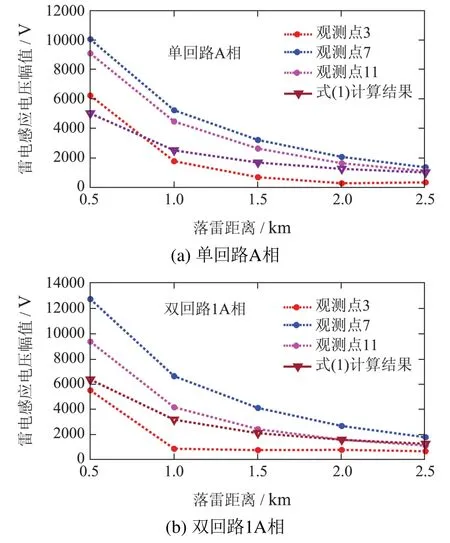
图13 雷电感应电压幅值随落雷距离的变化Fig.13 Variation of lightning induced voltage amplitude with return-stroke distance

由图11-12可知,落雷距离对架空线雷电感应电压的影响主要体现在脉冲幅值、脉冲上升时间和波形畸变程度.另外,部分观测点的“次脉冲”幅值也对落雷距离的变化较为敏感.各观测点雷电感应电压脉冲幅值均随落雷距离增大而明显降低,这是由于导线上的电场强度随辐射源与导线间距离增大而降低,致使感应电压激励源强度减弱.

同样以式(1)计算对象(观测点7)为对比对象,若以本文数值计算结果为标准,图14(a)和图14(b)分别给出了式(1)计算结果与标准值之间的幅值差(ΔUg)和幅值的相对误差(δS).由图14 可见,当回击距离由0.5 km增至2.5 km时,式(1)计算单/双回路雷电感应电压的ΔUg分别由约−5000 V和−6400 V降至约−360 V和−530 V,δS由约−52%分别降至约−26%和−29%.由此可见,式(1)基于静电理论计算雷电感应电压的静电分量,无法体现地闪电磁场场强随回击距离(回击通道与观测点间地面距离)的变化及该变化对雷电感应电压的影响,其计算误差的总体趋势为随回击距离减小而增大.值得注意的是,虽然式(1)的δS总体趋势随落雷距离越近而逐渐变大,但δS最大值出现在S取1 km时而并非为S取0.5 km时,可见二者之间并非单调递变的关系.

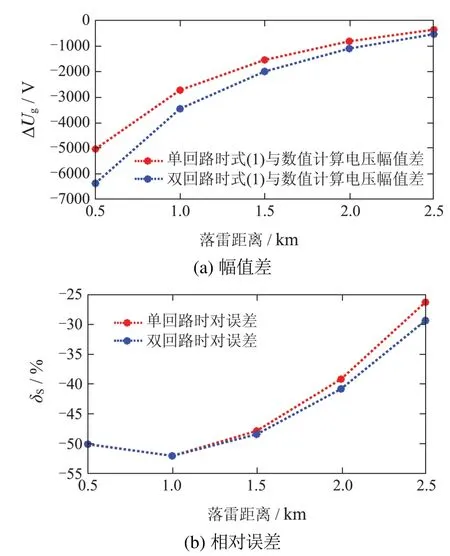
图14 落雷距离对式(1)计算误差的影响Fig.14 Influence of return-stroke distance on calculation error of formula(1)

另外,观察图11和图12中各观测点的雷电感应电压波形可以发现,电压脉冲波形在不同落雷距离时表现出不同程度的“波形畸变”.若将图11和图12进行整体对比,则不难发现,除落雷距离外,观测点位置和导线回路数也会对电压脉冲波形的畸变程度构成显著影响.3个因素对电压脉冲波形的整体影响趋势表现为:1)同一观测点的电压波形畸变程度随落雷距离的减小而增强;2)同一导线中观测点7的电压波形畸变最弱;3)相同情况下,双回路中观测点电压波形畸变程度较单回路明显加重.对于上述现象可基于地闪回击电磁场特性及Agrawal模型耦合机理进行理解.

1) 雷电感应电压的“入射”和“散射”激励源分别为回击电磁场与地面反射电磁场的叠加和导线中感应电流所产生的电磁场.除导线两端外两个激励源被分别等值为回击垂直电场和水平电场,水平电场的作用强度直接决定多导线间相互影响的强弱.另外,不同回击距离的地闪水平电场差异较大,这是由于水平电场由静电场、感应场和辐射场3个分量构成且前二者随回击距离增大而迅速衰减[25].水平电场的作用强度和复杂度均随落雷距离减小而增强,前者增加了导线间的相互影响,后者则直接影响感应电压波形.这二者作用的叠加导致雷电感应电压波形出现畸变且落雷距离越近畸变越严重.

2) 水平电场对导线的激励作用方向为导线轴向,在导线径向不产生作用.由图2可知观测点7几乎不存在水平电场的轴向分量,受水平电场影响微弱,因此其感应电压波形畸变最弱.

3) 在Agrawal耦合模型中,平行多导线雷电感应电压的散射激励源为所有导线中感应电流所激发的电磁场,因此导线间的互电容及互电感成为了其产生相互影响的媒介.导线数增多则导线间互电容和互电感的数量增加且结构更加复杂,导线间相互影响的强度增大.因此,相同情况下双回路较单回路雷电感应电压波形的畸变程度更严重.

由上述分析可知,落雷距离与雷电感应电压幅值成非线性关系,式(1)计算所产生幅值差和相对误差亦随落雷距离成明显的非线性关系.

4 结论

本文以解析算法中的计算参数为研究对象对雷电感应电压特性进行分析,并根据计算结果对解析算法的有效性进行了分析.得到以下结论:

1) 受地闪回击水平电场的影响,在20 m高度内雷电感应电压脉冲幅值随导线高度增大近似线性提高,脉冲上升陡度随导线高度增加而增加.

2) 回击电流幅值对雷电感应电压的影响仅体现在脉冲幅值,后者随回击电流幅值增大而线性提高.

3) 在2.5 km范围内随着落雷距离的减小,雷电感应电压脉冲幅值显著的非线性提高、脉冲上升时间有所降低、脉冲波形畸变程度明显加重.导线数越多,感应电压脉冲波形畸变越严重.

4) 解析算法所得雷电感应电压幅值随3个参数变化的趋势与数值计算较为相符,但存在显著的计算误差.以数值计算为标准,解析算法计算误差可高达45%～50%.