线性随机系统的微小传感器故障检测

牛艺春,刘诗洋,高 明,盛 立

(中国石油大学(华东)控制科学与工程学院,山东青岛 266580)

1 引言

随着现代工业对机器安全性与可靠性的不断重视,故障检测技术受到了学术界的广泛关注,在过去几十年里涌现出了丰硕的研究成果[1-5].纵观现有的研究成果,定量分析的故障检测方法可大致分为两类:基于解析模型的方法和数据驱动的方法[1].数据驱动的方法利用数据处理技术,在系统模型未知情况下进行故障检测,适用于大规模系统.但是对于动态机理已知的系统,基于解析模型的方法可利用精确的系统数学模型和可测数据构造残差,其检测性能通常要优于数据驱动的方法[2].

如文献[6-7]所述,故障可按照对系统影响的大小分为显著性故障和微小故障.微小故障是指一类具有微小的异常征兆的故障,如齿轮磨损引起的故障[8]、电路系统中的电弧放电故障[9].由于故障幅值过小或者所处环境噪声过大,微小故障对残差信号的影响通常会被未知的干扰和噪声所淹没,常用的故障检测手段难以检测到微小故障.另一方面,微小故障经过一段时间可能演化为显著性故障,对系统的安全运行构成重大威胁.因此,微小故障检测问题成为了当前工业界和学术界亟待解决的棘手问题,具有重要的研究意义.

近年来,由于工业界的迫切需求,微小故障检测技术得到了一定的发展[10-13].例如,文献[10]研究了基于数据驱动方法的微小故障检测问题.文献[12]通过区间滑模观测技术研究了中国高铁牵引装置中的微小传感器故障检测问题.文献[13]基于Kullback-Leibler散度方法设计了线性随机系统的微小传感器故障检测方案.在现有的基于模型的微小故障检测方法中,通常只能定性地说明微小故障检测的有效性,缺乏定量分析的结果.目前仍有一些关键问题有待解决,如故障误报率和漏报率的实时评估、故障幅值与故障可检测性之间关系的定量分析.

受上述文献的启发,本文从定量分析的角度研究了一类线性随机系统的微小故障检测问题.本文的主要贡献包括:1)基于移动加权平均方法设计了一种微小故障检测算法;2)定量分析了故障幅值、故障检测误报率和漏报率以及移动平均方法的窗口长度之间的关系;3)给出了确保微小故障在统计意义下可检测的最小窗口长度和最优权值矩阵.

2 问题描述

考虑一类线性随机系统

假设1(C,A)满足能观性判据.

其中Jth是设定的阈值.

考虑到系统(1)受到随机噪声的影响,可能发生故障误报和漏报的情况.根据文献[14],故障的误报率和漏报率定义如下:

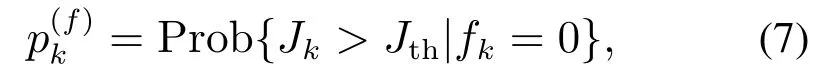
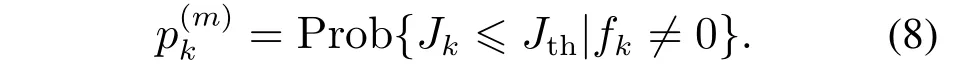
受到文献[15]的启发,给出如下的故障可检测性定义.

注1正如文献[15]所述,由于随机噪声的影响,故障的误报、漏报以及检测时延通常是不可避免的.因此,本文综合考虑了误报率、漏报率和检测时延,提出了故障在统计意义下的可检测性定义,确保了在无故障时,误报率低于给定上界;在故障发生一段时间后,漏报率也会低于给定上界.

随机系统故障检测的主要难点体现在如何区分故障与噪声对评价函数的影响.对于微小故障而言,由于噪声过大或者故障幅值过小,微小故障可能会被噪声淹没,漏报率远远超出给定上界.因此,本文的主要研究目标是设计合适的评价函数和阈值,确保微小故障满足统计意义下的可检测性.

3 主要结论

本节将给出微小故障检测的设计方法,分析微小故障在统计意义下的可检测性.

为了提高评价函数对故障的敏感程度,引入移动加权平均算法设计如下残差:

我的姐姐们整天跟着父亲下地，不是薅草，就是栽苗挖苕，总有干不完的活儿。母亲虽然不允许我走出院子，但她有时候竟忘了我的存在。她喂了更多的鸡和猪，每天要打几背篓的草，还要切细剁碎，哄着那些牲口吃光。我沉闷极了，孤零零地坐在院子边，等着有人经过时和我说上几句话。

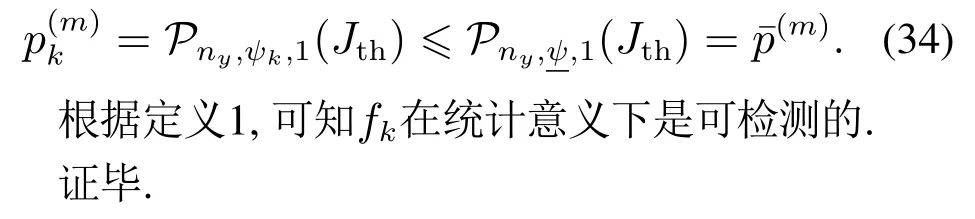
注5根据式(20),可以发现故障对评价函数的影响是动态变化的.在实际应用中,由于故障发生时刻kf是未知的,故障对评价函数的影响难以精确刻画.本文利用Kalman滤波器的性质,分析了故障发生后评价函数的最终趋势.在定理1中,设计最优权值矩阵和最小窗口长度,确保了在故障发生一段时间后,可以使得漏报率低于给定指标.

由于非中心卡方分布的累积分布函数形式复杂,ψ可能难以得到,给出如下的推论.

综上所述,给出系统(1)的微小故障检测算法如下.

算法1微小故障检测算法.

步骤1给定

步骤2利用MATLAB迭代计算出.若ny为偶数,利用式(36)和定理1得到最小窗口长度N和权值Ξs.若ny为奇数,利用推论1计算出合适的窗口长度N和权值Ξs.

步骤3当k ＞0时,系统运行,采集输入输出数据.

步骤4利用式(2)-(5),构造状态估计器.

步骤5利用式(9)和式(14),计算残差和评价函数.若Jk≤Jth,则判定故障没有发生;反之,则判定故障发生.

步骤6令k=k+1,返回步骤3.

注6正如文献[17]所述,非中心卡方分布的累积分布函数是一个极度复杂的函数.当自由度为偶数时,非中心卡方分布的累积分布函数可以通过如下公式求得[21]:

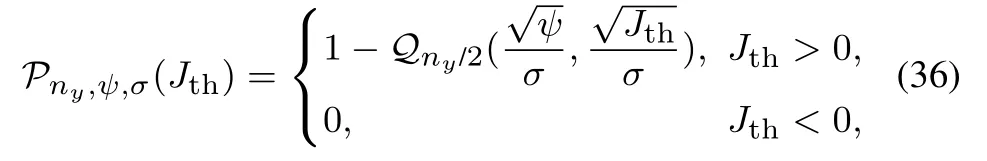
其中Qm(a,b)是广义马库姆Q函数,可通过MATLAB计算得到.此时,最小的窗口长度可通过试凑法得到.然而,当自由度为奇数时,无法直接计算出非中心卡方分布的累积分布函数,此时,可利用推论1的结论求出合适的窗口长度.由于推论1中利用了不等式缩放,所得窗口长度要大于最小长度.

4 算例

为验证上述方法的有效性,考虑如图1所示的车辆横向动力学系统,系统模型如下[14]:

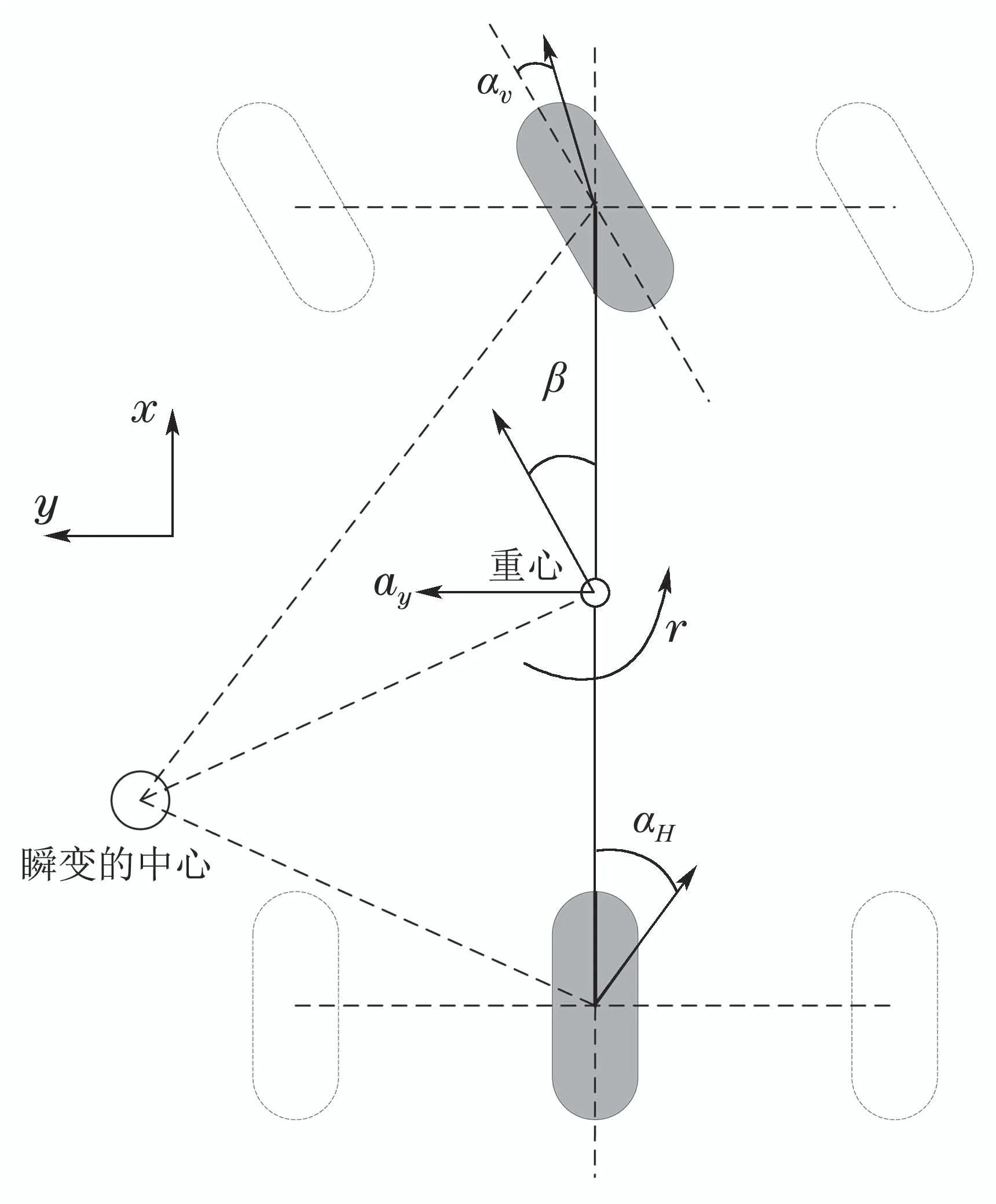
图1 车辆横向动力学系统Fig.1 Vehicle lateral dynamic system

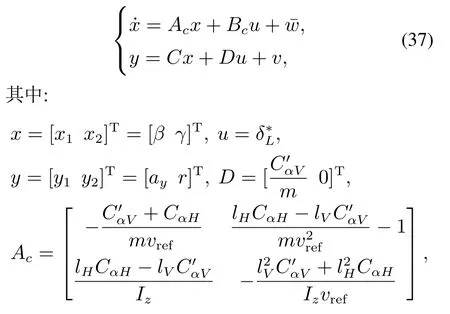
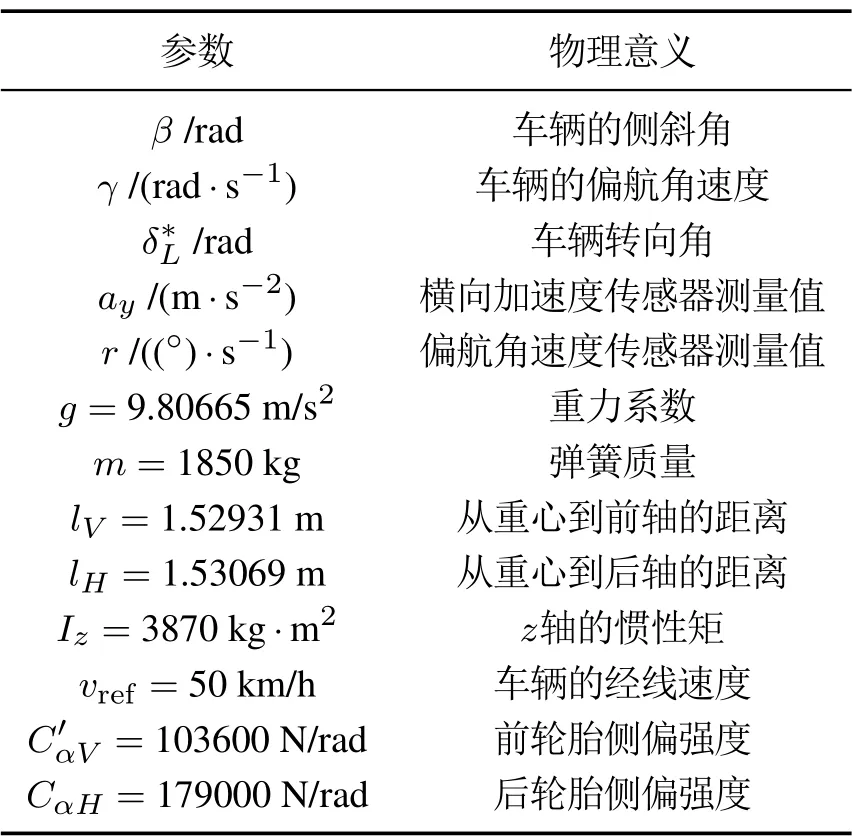
表1 系统(37)的参数Table 1 The parameters of system(37)

当采样时间为0.1 s时,系统(37)可以离散为具有如下参数的系统(1):

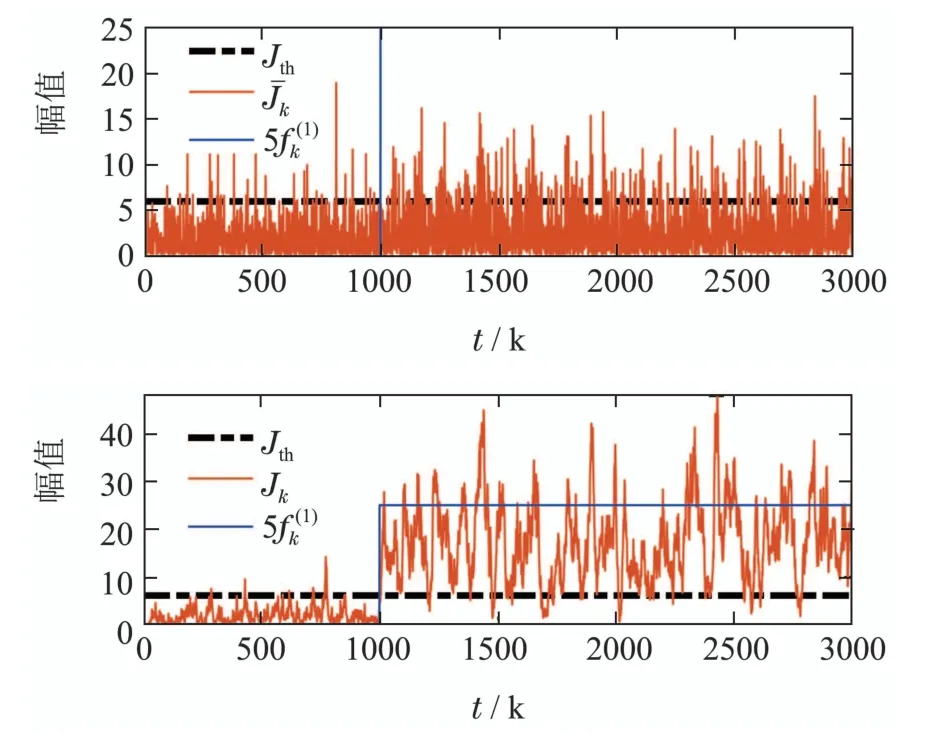
图2 故障发生时的检测结果Fig.2 The detection results when fault occurs

为了进一步验证故障检测器的误报率,漏报率与窗口长度的关系,采用蒙特卡洛法,统计故障检测器的实际误报率与漏报率.给定误报率为(f)=0.05,则阈值给定为Jth=5.99.定义实际误报率为

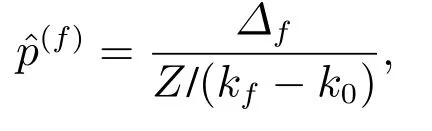
其中:Z=100为仿真次数,kf=1000为故障发生时刻,k0=0为仿真初始时刻,Δf为仿真过程中误报发生的次数.定义故障的实际漏报率为

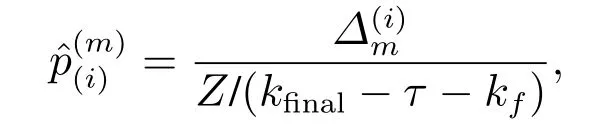
其中kfinal=3000为仿真终止时间,为仿真过程中漏报发生的次数,τ=500为检测延时.给定窗口长度,利用式(36)计算出故障发生时的漏报率理论结果为.表2给出了不同窗口长度下的误报率和漏报率的理论值与真实值的对比结果.仿真结果说明了在所设计的方法中,误报率和漏报率的理论值与真实值几乎一致.因此,可以通过调节移动加权平均方法的窗口长度,定量地调节故障检测器的漏报率,与此同时,故障的误报率不会受到影响.

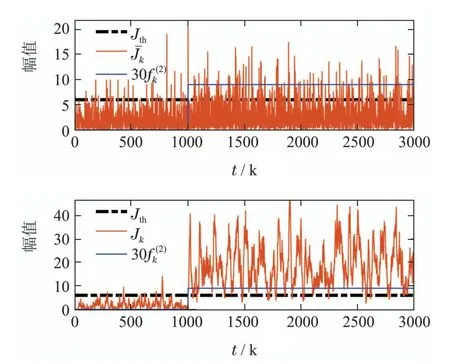
图3 故障发生时的检测结果Fig.3 The detection results when fault occurs

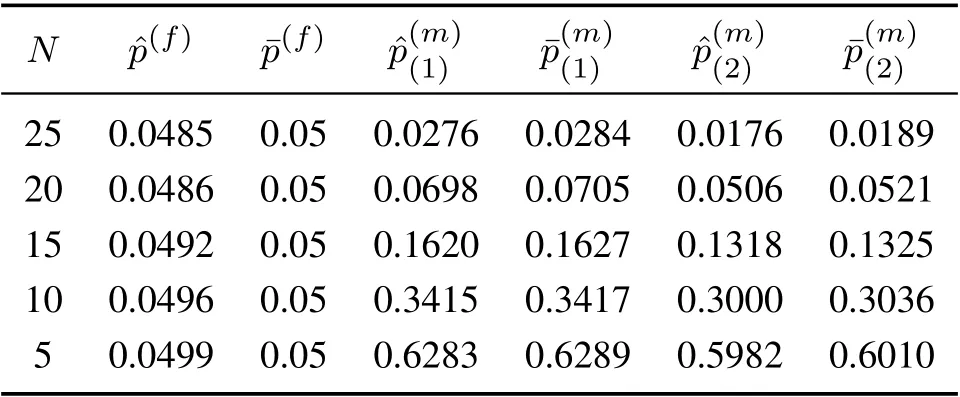
表2 不同窗口下实际误报率与漏报率Table 2 The actual false alarm rate and missed detection rate with different windows

注7与现有的基于模型的微小故障检测方法[12-13]相比,本文定量分析了故障检测器的误报率,漏报率与移动加权平均方法的窗口长度之间的关系.通过理论分析和仿真验证,都可以看出窗口长度的增大将有助于检测更小幅值的故障,但是与此同时会引起更长的检测时延.本文所设计的方法可以求得保障故障可检测性的最小窗口长度,有效降低了检测时延.

注8目前,已有文献定量分析了故障检测的误报率与漏报率[14-15].例如,文献[14]利用Neyman-Pearson准则、最大后验概率准则或贝叶斯准则设计合适的阈值,在给定的指标下优化误报率和漏报率.然而,由于微小故障的幅值很小,上述方法所得的最优误报率和漏报率也可能远高于设定值.本文基于移动加权平均方法设计残差和评价函数,引入了移动窗口可以有效提高评价函数对故障的敏感性,确保了故障幅值较小时误报率和漏报率仍可以低于设定值.

5 结论

本文针对一类线性随机系统研究了微小传感器故障检测问题.基于Kalman滤波算法,得到了随机系统的滤波器.然后利用移动加权平均方法,设计了残差和评价函数.通过对故障幅值、窗口长度、误报率和漏报率之间关系的定量分析,得到了最优的权值矩阵和最小窗口长度,并分析了微小故障在统计意义下的可检测性.最后,通过车辆横向控制系统仿真实验,验证了所提算法的有效性.相比于现有故障检测算法,本文方法可以通过改变窗口长度定量调节故障检测器的误报率和漏报率.在本文结果基础上,后续可以开展的工作有:1)将本文的结果推广到时变系统与非线性系统中;2)考虑非高斯噪声情况下的微小故障检测问题;3)考虑网络化现象对微小故障检测的影响[22].