融合强化学习和进化算法的高超声速飞行器航迹规划

池海红,周明鑫

(哈尔滨工程大学智能科学与工程学院,黑龙江哈尔滨 150001)

1 引言

高超声速飞行器具有快速响应、大航程、高效摧毁和强突防能力等突出优点,在飞行过程中,如果能够有效地实施机动飞行,就能避开障碍或威胁区域,从而提高生存概率.但是,由于高超声速飞行器的复杂特性,很难对这种控制对象进行路径规划和控制.宋建梅等[1]对远程导弹的运动模型进行离散化处理,运用A∗[2]算法来进行三维的航迹规划.李春华等[3]提出的稀疏A∗则将每次的搜索空间限制在满足无人机性能约束的范围内来进行航迹规划.上述研究均保证了规划的航迹满足实际对象的飞行需求,但是并不适用于存在动态威胁的情况,对环境的适应性也差.

相反,强化学习(reinforcement learning,RL)具有较好的实时性、优秀的泛化表现和设计流程的通用性等优点,使得它在机器人、无人机等领域的路径规划问题上均取得了优异的表现.Faust等[4]运用概率路线图(probabilistic roadmaps,PRM[5])在大型地图上分割出多个局部目标点,然后由深度确定性策略梯度(deep deterministic policy gradient,DDPG[6])训练的RL智能体引导机器人朝局部目标点移动,解决了复杂环境下机器人的远距离路径规划问题.Bae等[7]以整个地图图像作为RL 智能体的观测状态,采用的深度Q 网络(deep Q networks,DQN[8])算法在静态和动态障碍物的环境中表现出了优于A∗和D∗[9]的效果.上述方法均基于无模型的强化学习(model-free rein-forcement learning,MFRL),并且均使用“离线训练+在线使用”的模式,但没有探讨在线使用阶段RL智能体失败时的应对措施.尽管可以将离线训练阶段使用的梯度优化方法用于在线使用阶段继续对RL智能体进行训练来作为应对措施,但这过于耗费计算资源并且降低了实时性.

交叉熵方法(cross-entropy method,CEM)是一种简单、高效、易于并行和不依赖于梯度计算的优化方法.在控制问题中,CEM常被作为基于模型的强化学习(model-based reinforcement learning,MBRL)框架中优化策略的首选方法[10-11].Yang[12]等基于MBRL框架将CEM应用于现实世界的四足机器人的步态控制问题.除此以外,Pourchot[13]等将CEM 和DDPG,双延迟深度确定性策略梯度(twin delayed deep deterministic policy gradient,TD3[14])算法相结合,在训练期间,利用CEM和原本的梯度优化方法对参数化的RL智能体的策略参数进行优化,该方法有效提升了DDPG和TD3的性能,Pourchot等的研究中也表明了仅仅采用CEM进行策略参数的优化效果是不佳的.

总之,近几年新提出的强化学习理论,如DQN,DDPG等表现出了高于传统路径规划算法的自主性、实时性和对环境的适应性.然而,这些新理论在高超声速飞行器的航迹规划问题上的应用研究相对较少.孟中杰等[15]在稀疏A∗算法中引入了变步长策略来有效提高了规划效率,但是规划期间无法处理威胁数量动态变化的情况.为此,沈海冰等[16]对变步长的稀疏A∗算法进行改进,将D∗算法的思想引入其中,在新威胁与已规划的航迹相交时进行局部重规划,实现了在线实时航迹规划.

在考虑航迹长度最小、航迹曲率(需用过载)的平滑性和飞行器过载约束的前提下,本文利用MFRL和CEM来解决高超声速飞行器巡航段的航迹规划问题.在离线训练阶段,本文设计了可以处理动态威胁数量的网络结构,利用全局信息对RL智能体进行训练,并对比了屏蔽部分信息后对训练结果的影响,全局信息包括了飞行器的位姿信息、威胁和目标点的坐标信息等.在在线使用阶段,本文将MFRL和CEM结合,提出了RL-CEM规划方法,该方法仅仅利用CEM来优化RL智能体的规划策略.同时,设计了一种简单有效的动作过滤器来保证航迹曲率(需用过载)的平滑性.实验结果表明了,让RL智能体获得更丰富的环境信息可以提高其性能,以及RL-CEM具有令人满意的航迹规划的成功率.最后,本文在威胁分布密集、威胁数量动态变化、存在动态威胁、威胁呈U型分布的特殊环境中验证了RL-CEM的鲁棒性.

2 高超声速飞行器航迹规划

2.1 问题阐述

本文针对高超声速飞行器的巡航段,对其航迹规划问题进行研究.本文中将雷达阵地、高炮阵地和禁飞区等影响飞行器安全的区域或不可飞区域统称为威胁.假设C为整个作战空域中飞行器位姿点p=(x,y,z,θ,ψv)的集合,这里(x,y,z)代表飞行器所在位置或航路点,(θ,ψv)分别代表飞行器的弹道倾角和弹道偏角.Csafe⊂C为飞行器与威胁不相交的位姿点的集合.航迹P由一系列的位姿点pi组成,pi ∈C,i ∈[0,k],该航迹始于p0结束于pk,对于任意两个连续的位姿点pi和pi+1,i=1,···,k −1,从pi经过一个固定的离散时间步长ΔT均可到达pi+1.给定一个有效的目标位姿点pg,如果航迹P中的任意一个位姿点pi/∈Csafe或者飞行器超过飞行任务限定的执行时间Tmax,则该条航迹不满足任务约束.如果航迹P中的任意一个位姿点均满足pi ∈Csafe,飞行器未超过飞行任务限定的执行时间Tmax,且pk与pg的欧氏距离满足给定阈值,即‖pk −pg‖≤dg,则该条航迹规划满足任务约束,本文称这种满足任务约束的航迹为有效航迹.本文的最终目的是在给定的作战环境中,利用RL求解这样的一条有效航迹.

高超声速飞行器为了减小气动加热,其巡航段的飞行高度都较高,因此对其巡航段进行航迹规划时不用考虑地形、障碍等因素.于是,本文进行如下假设以简化航迹规划问题:1)高超声速飞行器等高等速飞行;2)已知威胁区域的位置和覆盖范围;3)威胁均为无限高的圆柱体.

这样,三维空间的航迹规划问题就可以简化为二维平面的航迹规划问题,这有效地降低了问题的复杂度.于是,本文可以重新定义位姿点p=(x,z,ψv)和相关关系式.

二维平面的高超声速飞行器运动学方程如下:

式中:x和z是飞行器质心在地面坐标系下的位置坐标;v是飞行器的巡航速度;ψv是弹道偏角.

过载与弹道形状的关系式如下:

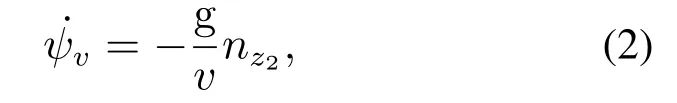
2.2 航迹规划方法

高超声速飞行器造价高昂,将强化学习应用于真实的高超声速飞行器上时,样本效率是首先需要考虑的问题.因此,本文建立了一个环境模拟器来模拟真实的飞行环境.由于本文研究的是高超声速飞行器的航迹规划问题而非制导问题,因此虚拟环境中的飞行器建模为一个简易的模型,它能够立即响应给定的指令.

强化学习方法通过与环境交互,学习状态到动作的映射关系,它可以解决离散时间的马尔可夫决策过程问题.本文从局部可观和完全可观的角度,将航迹规划问题建模为部分可观的马尔可夫决策过程(partially observable Markov decision process,POMDP)和完全可观的马尔可夫决策过程(Markov decision process,MDP),关于二者的描述见第2.3节.这里,本文将POMDP 模型用五元组〈O,A,R,P,γ〉来表示,MDP模型则用五元组〈S,A,R,P,γ〉来表示.除了特别说明,本文中POMDP模型的状态o ∈O和MDP模型的状态s ∈S均使用s来表示.

本文的航迹规划分2个阶段:1)离线训练阶段,训练一个不依赖于固定环境的RL智能体作为航迹规划的基线策略;2)在线规划阶段,RL-CEM利用环境模拟器预测未来的状态进行规划,之后,选择优于基线策略的策略作为执行策略,否则将使用基线策略.

第1阶段,构建环境模拟器来模拟真实的飞行环境,该虚拟环境中存在飞行器、威胁和目标.环境模拟器在每次重置时,均会设定一个随机的初始位置给飞行器、威胁和目标,这可以保证RL智能体的规划策略不依赖于固定的环境.该阶段的最终目的是:训练一个RL智能体去控制虚拟飞行器在虚拟环境中成功地执行突防任务.换句话说,RL智能体需要在一个与其动作a相关的转移函数=f(p,a)下(本文中该转移函数意味着虚拟环境),使得生成的航迹的所有位姿点pi,i=1,···,k,满足pi ∈Csafe,且‖pk−pg‖≤dg,转移函数表明了完成任务的条件仅仅取决于RL智能体能观察到什么以及它由此做出的行动.最终,训练结束的RL智能体将作为在线规划阶段的基线策略.

第2阶段,RL-CEM规划最优策略作为执行策略,执行策略则通过与环境模拟器的交互生成有效的航迹.图1描述了这一流程.RL-CEM首先使用CEM规划一个CEM策略,该策略尽可能最大化从某一起始状态开始未来H个时间步的累积奖励,然后,选择基线策略和CEM策略中该累积奖励最大的策略作为最优策略,在下一轮规划期间,将该最优策略作为执行策略与环境模拟器交互.RL-CEM每隔Tp个时间步规划一次,用于规划的起始状态领先此轮规划开始时的实际状态Tp个时间步,该起始状态及其后续的状态均通过子模拟器预测.规划和执行操作是异步进行的,这保证了RL-CEM的实时性.在真实飞行器系统的每个采样时刻,环境模拟器发送此时虚拟飞行器的位姿点作为真实飞行器的期望位姿点.期望位姿点在时间上的平滑性则由动作过滤器来保证.环境模拟器将定期根据真实环境来更新其动力学.

图1 有效航迹生成流程图Fig.1 Flow chart of effective track generation

2.3 MDP模型和POMDP模型

本文构建的MDP和POMDP模型具有相同的动作空间和奖励函数,它们主要的区别在于状态空间的不同.

2.3.1 状态空间

POMDP的状态空间:在本文的POMDP模型中,RL智能体仅仅能够观测到环境中的局部信息,记观察到的状态为o ∈O,o ∈R30,则状态o包含:(x,z),飞行器的实时位置;(cosψv,sinψv),弹道偏角的信息,ψv,弹道偏角;,弹道偏角的转动角速度;v,飞行器的巡航速度;(xg,zg),目标的实时位置;(cosq,sinq),视线角的信息,q,视线角;F,目标线是否与威胁相交的标志位,条件为真表示相交;dray,在RL智能体视角正前方180°均匀分布19条长500 km的射线,dray包含了每条射线到最近的威胁边沿的距离信息,dray∈R19,这类似于激光雷达的原理.

MDP的状态空间:RL智能体能够观察到完整的环境状态,记它观察到的状态为s ∈S,MDP模型中的状态s除了包含POMDP模型中的信息以外,还包含了:,每个威胁的实时位置,i=1,···,N;(cosηi,sinηi),飞行器和威胁的连线与基准线之间的夹角信息,η为飞行器和威胁的连线与基准线之间的夹角,i=1,···,N;(cosh,sinh),当前经过的时间信息,h=2π·(T/Tmax),T为当前经过的时间步数.由上可知,威胁数量的不固定导致了该状态空间是动态变化的.

式中s ∈R32+4×N.本文假设这样的一个状态包含了所有的环境信息.

2.3.2 动作空间

考虑到在环境模拟器中没有对高超声速飞行器进行完整的建模,仅仅建立了满足飞行器运动学模型的虚拟飞行器,所以无法将RL智能体的动作设定为舵偏角.并且,本文生成的航迹的需用过载必须要满足约束.因此,本文将动作a定义为最大角速度的比率,可以得到a与的关系式如下:

本文中,MDP和POMDP模型的动作空间是一致的,均使用该小节描述的动作空间.

2.3.3 奖励函数

RL智能体的任务目标是避开不可飞的区域抵达目标,故奖励函数的设计可拆解为两部分:规避威胁和目标导航的奖励设计.规避威胁的奖励鼓励RL智能体不与威胁接触,目标导航的奖励则鼓励RL智能体不断接近最终的目标点.

规避威胁和目标导航的奖励相互耦合,使得奖励函数的设计变得困难.本文从两个方面来设计目标导航的奖励以降低不同奖励之间的耦合:当飞行器与目标点之间的连线与威胁相交时,通过相邻时刻飞行器与目标点的距离变化量设计距离奖励来引导飞行器;当不相交时,设计航向奖励来引导飞行器的速度矢量指向目标点.和的具体表达式如下:

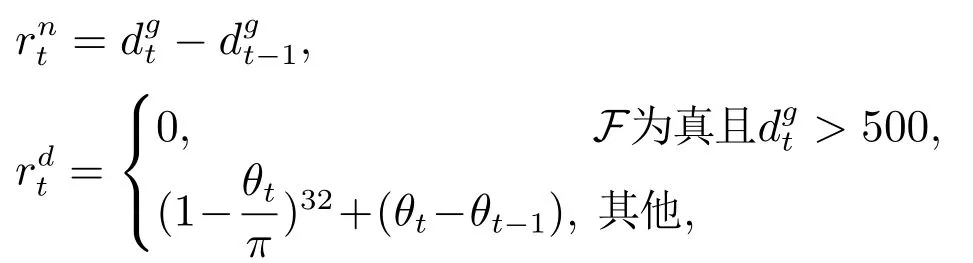
式中:表示t时刻飞行器与目标点的距离;θt ∈[0,π]表示飞行器的速度矢量与目标线之间的夹角.

另外,当飞行器抵达目标点时提供一个丰厚的奖励,该奖励与抵达目标所花费的时间成反比,定义如下:

式中:Tmax表示最大的分幕步数;T表示飞行器抵达目标花费的分幕步数;表示飞行器与目标点之间可允许的最小距离.

在航迹规划问题中,飞行时间也应该是考虑的指标.本文引入了一个时间惩罚以鼓励RL智能体尽可能快地抵达目标点,的定义如下:

最后,本文考虑了航迹需用过载最小的问题.由于RL智能体的动作a与弹道的需用过载成正比,因此,可以设计奖励

综上,MDP和POMDP模型的奖励函数定义如下:

式中k=[k1,···,k6],表示各项奖励的权值向量.

2.4 网络结构

RL智能体的策略由两个具有不同参数的独立网络组成:actor网络(策略网络)和critic网络(价值网络).Actor网络由状态信息得到一个动作分布,critic网络则预测期望的未来折扣回报.针对连续的动作空间,本文主要使用近端策略优化(proximal policy optimization,PPO[17])对策略进行优化.在本文中,定义参数φ为参数化的critic网络的参数,参数θ为的actor网络的参数.由于PPO中的critic网络预测的是状态价值V(s):给定状态的情况下,从当前状态往后的期望的累积奖励.于是,本文将actor网络表示为πθ(·|s),critic网络则表示为Vφ(s).

在本文的POMDP中,策略π可以采用如多层感知网络(multi-layer perception,MLP).MLP网络具有2个隐层,每个隐层有64个神经元,并使用relu作为激活函数,输出层则为线性激活函数.

在本文的MDP中,RL智能体能够直接观测到环境状态,由于环境中的威胁数量不固定,导致了状态空间的维度是动态变化的,因此,本文采用了一种基于自注意[18](self-attention)的结构化表征的关系推理机制[19-20]结合来解决.MDP中的策略和价值网络使用了图2所示的网络结构.

图2 MDP中的策略和价值网络Fig.2 Actor and critic in MDP

2.5 RL-CEM

强化学习本身是一种黑箱优化方法,通常情况下无法预知智能体的行为带来的危害.因此,为了保证在智能体发生异常时有一个有效的补救措施,本文将RL和CEM结合,在实际应用阶段通过CEM来对RL智能体的策略进行优化.为了方便说明,在这里,本文中POMDP模型的状态o ∈O和MDP模型的状态s ∈S均使用s来表示.

表1 RL-CEM的伪代码Table 1 Pseudocode for RL-CEM

本文中使用了MLP来近似CEM策略µθCEM,该网络仅由一个16个神经元的隐层构成,每一层的激活函数均使用了双曲正切函数tanh.

为了保证实时性以及最优动作序列不过时,本文采用了异步规划的方法:一个进程规划最优策略,一个进程执行规划的最优策略.这与文献[12]中的异步控制相似.

2.6 动作平滑

在本文的方法中,尽管能够保证RL智能体构建的航迹是平滑的,但是无法保证路径上的曲率变化平滑.本文分析得出曲率不平滑的问题是由于RL智能体相邻时刻的动作发生突变导致,即动作在时间上不具有相关性.也就是说,本文需要保证RL智能体给出的动作指令在时间上具有相关性.本文结合指数加权平均设计了2个不同的动作过滤器:动量过滤器和插值过滤器.为了方便说明,本文使用下标t表示RL智能体当前的决策次数,i表示当前模拟器的模拟次数.

式中:β=0.9;动作更新率α=0.005;clip(·,−1,1)函数将对应值截断在−1到1之间.

插值过滤器:通过指数加权平均计算RL智能体给出的动作a的局部平均值,以该局部平均值作为平滑后的动作,如式(12)所示.然后,本文通过Hermite插值得到相邻决策时刻动作的平滑过渡函数f(·),以此计算传递给模拟器的实际动作,该过渡函数由式(13)-(14)所示的约束条件插值得到,这能有效保证动作的平滑性.

式中ΔTagent表示智能体的决策频率.

3 实验结果与分析

3.1 训练设置

本文使用PPO算法训练RL智能体,表2中报告了相关的超参数.另外,本文额外引入了软演员-评论家(soft actor-critic,SAC[22])算法进行对比,超参数的选取则是文献[22]中提供的参考值的基础上额外使用了优先经验重放[23],并对奖励权值向量k进行了微调.本文的RL智能体规划的航迹满足表3所示的约束条件.除此以外,通过奖励函数的设计还尽可能的保证了航迹的需用过载最小和航迹长度(预估飞行时间)最小.训练环境中设置了15个半径50 km的威胁,每次重置环境时随机生成威胁的位置.

表2 训练阶段的超参数Table 2 Hyperparameters in the training phase

表3 航迹约束Table 3 Trajectory constraints

3.2 训练结果

本文在图3中报告了在3组随机数种子上的训练结果.训练结果表明,本文的建模方法在不同的RL算法上均可以达到相同的表现;PPO在训练过程中具有更稳定的表现;动量过滤器具有比插值过滤器更好的性能;MDP的方法比POMDP具有更高的样本效率,本文认为这得益于MDP中采用的网络结构以及全局信息的引入.

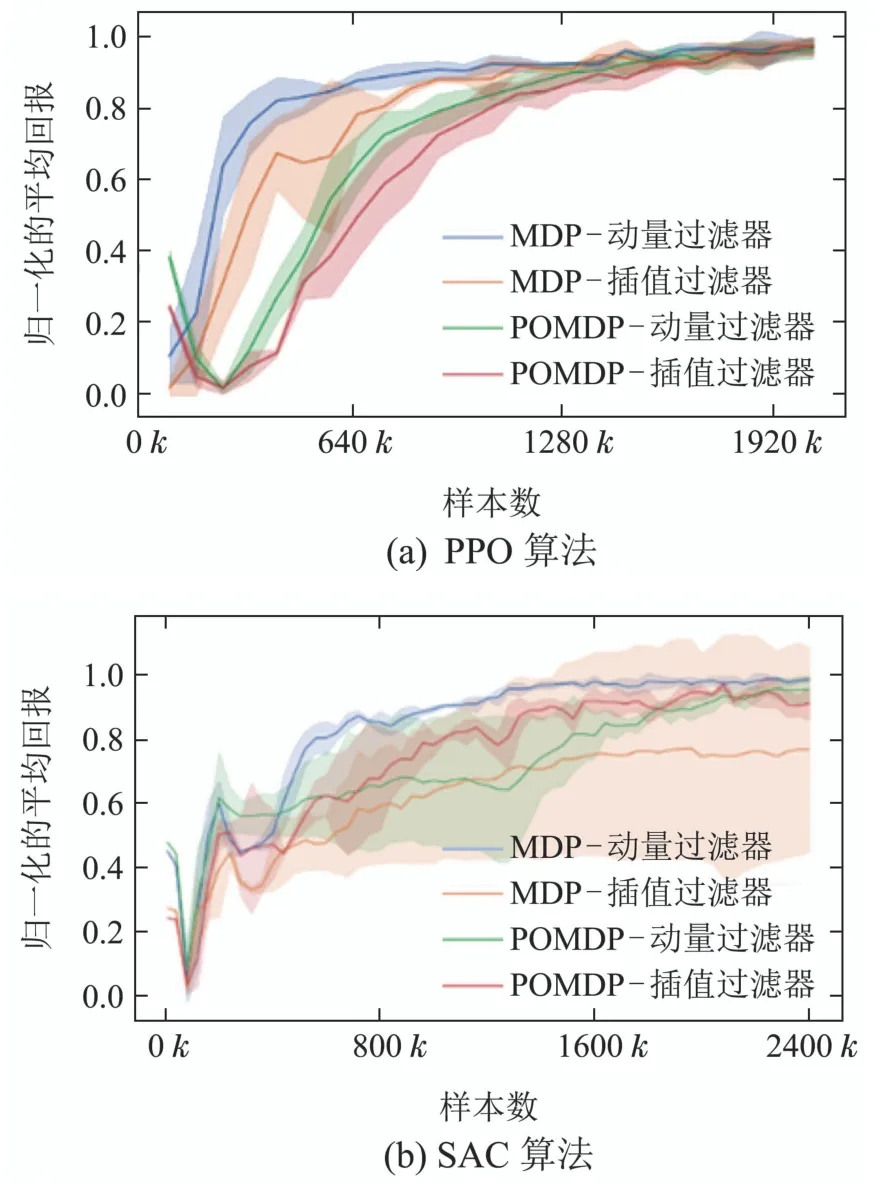
图3 训练曲线Fig.3 Training curve

由于PPO在训练过程中的表现更稳定,本文将主要使用PPO训练的智能体进行实验验证.图4中展示了部分成功案例和航迹需用过载的变化曲线.从图中可以看出,本文设计的动作过滤器有效地保证了需用过载的平滑性.

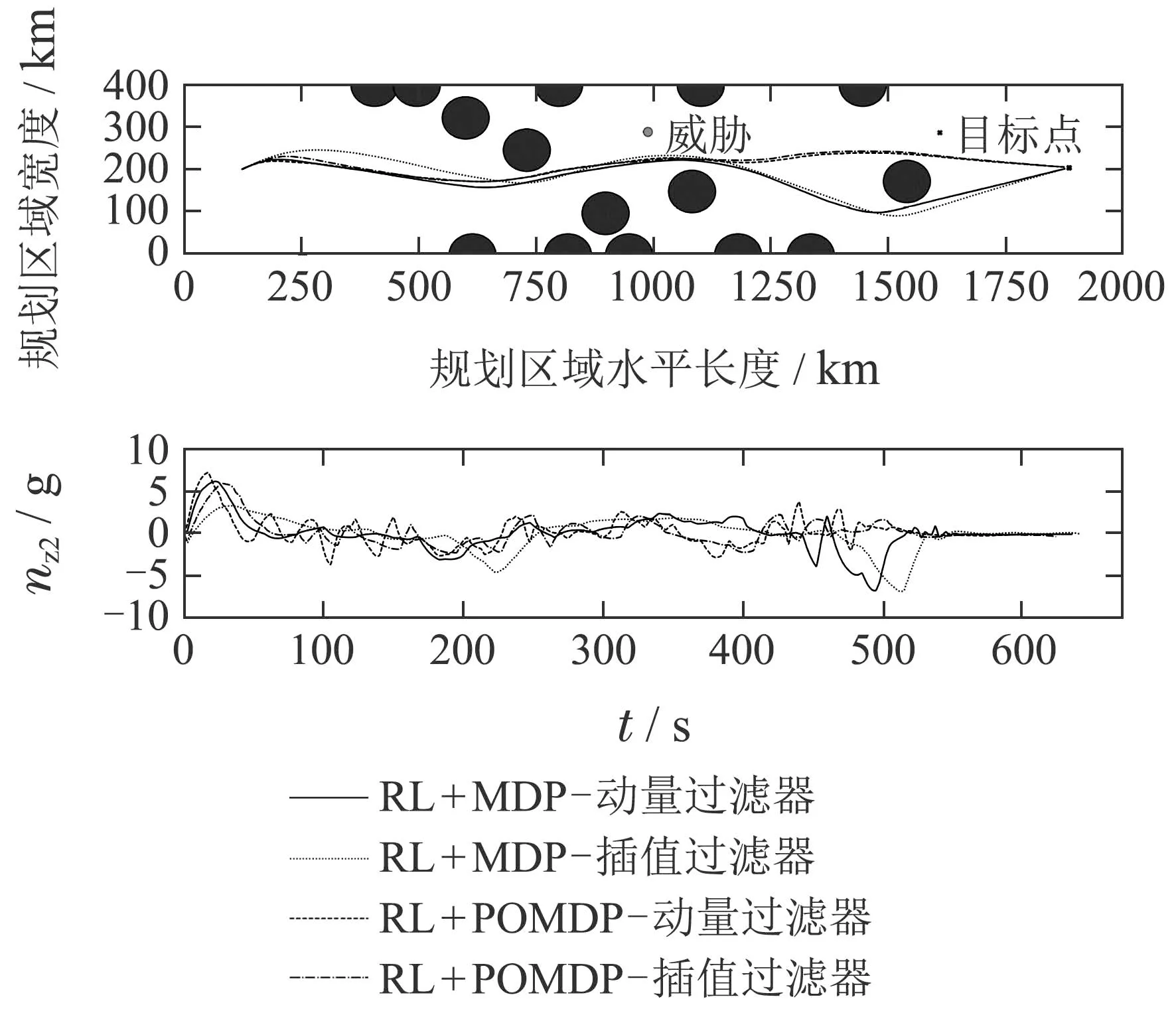
图4 部分成功案例Fig.4 Some successful cases

本文以突防成功率为评估指标,将经训练的所有RL智能体在训练环境中使用无探索噪声的策略评估了500 个分幕,RL-CEM 则评估了100 个分幕.RLCEM使用的超参数如表4所示.它们各自的突防成功率如图5所示,从图中可以看出,MDP中训练的RL智能体的突防成功率明显高于POMDP中的,并且在结合RL-CEM后,极大地提升了每一个RL智能体的表现,它们均达到了近乎百分百的成功率.综上,MDP中训练的RL智能体能够提供一个可靠的基线策略,该策略不仅可以用于规划,还可以作为突发情况时的备用策略,RL-CEM则弥补了RL智能体的缺陷,进一步提高了突防成功率.

图5 突防成功率Fig.5 Penetration success rate

表4 RL-CEM的超参数Table 4 Hyperparameters of RL-CEM

3.3 结果评估

跟踪RL智能体获得的最终回报是一个不够充分的评估指标,奖励的累积并不能明确表明智能体是在均衡的改进策略还是在停滞不前.因此,本文将使用通过PPO在MDP和POMDP中结合了动量过滤器训练的RL智能体来进行评估实验,以验证本文的航迹规划方法的鲁棒性,并将通过这些评估实验来回答下述的几个问题:

•是否可以应用于不同尺度的飞行地图中?

•是否可以处理不同大小和不同数量的威胁?

•是否可以应用于存在动态威胁的地图中?

•是否可以有效地避免局部最优?

除特别说明以外,下面的评估实验中,本文将使用表3中RL-CEM的超参数,RL方法和RL-CEM方法分别进行500个分幕和100个分幕的评估.

3.3.1 不同数量和大小的威胁

本文将威胁的数量从15个增加到了20个,每个威胁的覆盖半径在30 km到150 km之间随机选取.表5中报告了该节实验中不同方法的突防成功率.

表5 突防成功率-不同数量和大小的威胁Table 5 Penetration success rate-different numbers and sizes of threats

表5的实验结果中,MDP中训练的RL智能体的性能出现了明显的下降.为了分析原因,本文进行了进一步测试:在仅仅改变威胁数量的环境中,MDP方法的突防成功率为0.882;在仅仅改变威胁大小的环境中,则为0.778.可以得知,威胁大小的改变对MDP方法的影响较大.幸运的是,RL-CEM有效弥补了RL智能体航迹规划失败的情况,实验结果进一步证实了RL-CEM的可靠性和鲁棒性.

3.3.2 动态的威胁

本文将威胁的运动学模型建模为线性恒速模型,每个威胁的运动速度0.1 km/s,运动方向则在0°～360°之间随机选取.表6中报告了该节实验中不同方法的突防成功率.实验结果表明,无论是单纯的RL方法还是RL-CEM方法,均避开了动态威胁成功抵达了目标点.可见,本文的航迹规划方法对于存在动态威胁的地图具有令人满意的鲁棒性.

表6 突防成功率-动态的威胁Table 6 Penetration success rate-dynamic threats

3.3.3 回避局部最优

路径规划问题中,U形障碍物是这一类问题中的难点:U形障碍物会形成一条死路,从而导致路径规划失败、延长规划时间或者路径长度.移动机器人、四旋翼等在遇到U形障碍物时可以凭借自身的机动优势离开.然而,高超声速飞行器无法倒退或者原地转向,一旦进入呈U形密集分布的威胁时,它必须进行大机动转弯来反向飞行才有可能飞离该区域,但是,无法保证这一定能成功,并且能量的花费也不容忽视.欲解决这一问题,需要RL智能体能提前避开这样的威胁区.

由于该节是针对特定威胁布局的情况进行实验,所以仅仅只进行单个分幕的评估.本文在如图6上半部分所示的地图中进行了评估实验,实验中飞行器的飞行速度v设置为3.0 km/s.图中显示,单纯的RL智能体难以在这样的环境中规划一条有效的航迹,但是,结合RL-CEM后均成功地抵达了目标点.可见,RLCEM弥补了RL方法的不足.需要注意的是,RL-CEM的规划长度直接影响着是否能够回避局部最优,短的规划长度同样会使得RL-CEM陷入更糟糕的局部最优,长的规划长度则可以避免这样的情况.尽管增加规划长度会提高规划的时间开销,但是,RL-CEM的规划时间开销仅仅集中于在环境中采样这一阶段(算法1中6-9行),这可以通过并行化采样来极大地缩短时间开销.因此,规划长度的增加对规划时间的影响是很小的.

图6 呈U型分布的威胁区Fig.6 U-shaped threat zone

4 结论

1) 本文考虑了需用过载最小、飞行时间最短和需用过载的平滑性,讨论了在过载约束下的航迹规划问题.本文将航迹规划问题建模为POMDP和MDP,通过PPO来求解POMDP和MDP问题,并引入指数加权平均来设计动作过滤器以增加RL智能体的动作在时间上的相关性,在几乎不带来额外计算开销的前提下,保证了航迹的需用过载的平滑性.在实验中,MDP方法体现了利用全局信息进行规划的优势,提出的RL-CEM不仅有效地回避航迹规划中的局部最优,还展现出了令人满意的成功率.RL-CEM弥补了以往基于RL的航迹规划方法容易陷入局部最优、规划失败时无替代方案的缺点.最后,本文的RL-CEM方法在不同的特殊环境中也展现出了令人满意的泛化性能.

2) 本文的RL-CEM方法在进行规划时,需要通过并行化来缩短规划时间以保证实时性,这使得执行规划的计算机需要满足一定的性能要求.

3) 本文的航迹规划方法回避了高超声速飞行器复杂的动力学,仅通过其运动学来解决该问题.本文的下一步工作将结合高超声速飞行器的动力学,从姿态控制到制导来进行完整的高超声速飞行器的航迹规划研究.