分布滞后非线性模型的多元meta分析在R软件中实现

陈东真 尹 嘉 丁国永 刘志东 刘雪娜 陆 华 李晓梅

1 山东第一医科大学(山东省医学科学院)，271016 山东 泰安；2 聊城市疾病预防控制中心，252000 山东 聊城；3山东大学齐鲁医院，250012 山东 济南；4 泰安市疾病预防控制中心，271001 山东 泰安

环境暴露对健康的效应一般采用多个研究地点的数据进行时间序列分析，这种情况通常采用2阶段分析方法。首先采用回归模型分析暴露反应关系，然后采用meta分析将多个研究地点的效应进行合并。而环境暴露对健康产生的效应一般会存在滞后，且暴露与结局的关系呈现非线性关系，因此在第一阶段常采用分布滞后非线性模型(distributed lag non-linear model, DLNM)来模拟环境暴露与健康结局的关系。DLNM是在广义线性模型、广义相加模型的基础上，加入交叉基函数，可以同时灵活地评估时间序列数据中非线性暴露—反应关系以及滞后效应[1]。针对非线性暴露—反应关系，在第二阶段可采用多元meta分析[2]，对各研究地区估计的参数进行合并，获取环境暴露对健康的总效应。

杨金建等[2]针对DLNM以及多元meta模型的原理进行了详细阐述，但是在实例分析部分并未展现结果实现的具体步骤。因此，本研究使用R软件，以2005—2016年山东省9个地级市平均气温与肺结核报告发病数据为实例，利用“dlnm”包实现DLNM模型和“mvmeta”包实现多元meta分析。

1 DLNM模型及多元meta分析方法简介

为获取环境暴露对健康的总效应，可采用混合式分析方法进行，包括非线性暴露—反应关系的DLNM模型与提取，并合并各地区参数值的多元meta分析。

1.1 DLNM模型

广义相加模型只考虑暴露反应关系，分布滞后线性模型没有解决暴露与结局的非线性关系，由此发展了同时在暴露和滞后维度引入非线性关系的DLNM[3]。DLNM是以交叉基为核心，暴露—反应关系与滞后效应分别选取相应的基函数，计算2组基函数的张力积得到交叉基函数。基函数主要包括多项式函数、自然立方样条函数、线性阈值函数、惩罚样条函数，最常用的是自然立方样条和惩罚样条。DLNM基本表达式：

其中，μt=E(Yt)，Yt代表结局变量，该结局变量符合指数分布族，例如正态分布、Gamma分布和Poisson分布等，E(Yt)代表t时刻因变量Y的期望；g代表连接函数；sj代表xj与E(Yt)间的非线性函数；uk代表其他与E(Yt)间存在线性关系的变量；β、γ分别代表xj、uk的参数向量。sj代表自变量xj的基函数，通过选择不同的基函数可将xj转换成一个新的变量集，包含到模型的设计矩阵中，并进行参数估计。

1.2 多元meta分析

meta分析是对多个研究目的相同的研究结果进行综合分析，以使用量化的平均效果来解决研究问题的一种研究方法[4-5]。meta分析通常假设各研究之间是独立的，而许多研究之间并不是相互独立的，因此在meta分析的基础上扩展出了多元meta分析。

多元meta分析可以利用研究之间和/或研究内部的相关结构产生更有效或更精确的估计，此方法考虑到了各结果之间的相关性，克服了单变量meta分析方法忽略相关结构的局限性[6]。对于随机或者信息缺失，需要汇总数据结局的研究，该方法是更好的选择。使用多元meta分析进行分析时，主要包括随机效应模型与固定效应模型。异质性检验使用Q检验中的P值，来选择效应模型。在第一阶段得到的研究内协方差矩阵，包括每个研究效应的方差及其协方差，在多元meta分析阶段时，将这些估计值进行合并[7]。

本研究灵活利用R语言“dlnm”包与“mvmeta”包实现DLNM模型与多元meta分析。通过实例分析，展现采用本研究的R语言代码，利用原数据快速、直接地实现DLNM模型与多元meta分析相结合的两阶段统计分析方法。

2 实例与R软件分析

2.1 资料概述

现以山东省威海市、烟台市、青岛市、东营市、潍坊市、日照市、滨州市、淄博市和临沂市的气候变量与肺结核报告发病数据集为例，演示DLNM与多元meta分析，合并多个地级市的非线性暴露—反应效应。本研究数据集包括每日平均气温、相对湿度、日照时数、平均风速、降水量和肺结核报告发病数，见表1。

表1 2005—2016年平均气温对肺结核发病影响的数据资料

2.2 数据的导入与数据的预处理

library(readxl)#加载readxl包

Shandong<-read_excel("D:/Shandong.xlsx")#数据集导入

regions <-as.character(unique(Shandong$cityname))

data <-lapply(regions,function(x)Shandong[Shandong$cityname==x,])

names(data)<-regions

#创建地区序列的列表

ranges <-t(sapply(data, function(x)range(x$Atemp,na.rm=T)))

#创建一个数据框，命名为ranges，该数据框是各地级市平均气温的最大值和最小值

2.3 对单个地级市利用“dlnm”与“splines”包构建DLNM模型

library(dlnm)#加载dlnm包

city <-"Qingdao" #选取青岛市，命名为city

cen<-quantile(Atemp,0.50)

cb<-crossbasis(data[[city]]$Atemp,lag=90, argvar =list(df=3,fun="bs",cen=cen), arglag =list(df=3,fun="ns"))

summary(cb)

#建立交叉基。对自变量与因变量的关系、滞后效应分别选择合适的基函数，2个基函数的张力积即得交叉基。lag设置最大滞后天数90 d；参数argvar控制平均气温与肺结核报告发病率的关系，自由度设置为3，基函数采用二次B样条函数，参考值采用平均气温的中位数；参数arglag控制滞后效应，自由度设置为3，采用自然立方样条函数。summary(cb)可以查看交叉基参数设置情况。

library(splines)#加载splines 包

model<-glm(PTB～cb+ns(time,7*12)+dow+Season+ns(SD,3)+ns(ARH,3)

+ns(AWS,3)+ns(PRE,3),family = quasipoisson(),data[[city]])

summary(model)

#模型的建立。调用自然立方样条函数，运用quasipoisson控制Poisson回归的过离散现象，时间的自由度选取最常用的7，气象变量的自由度选取3。

bound <-colMeans(ranges)#设置边界值

cp <-crosspred(cb,model,from=bound[1],to=bound[2],by=1)

d3 <-plot(cp,xlab="Tempeature/℃", ylab="Lag/d", zlab="RR",theta=200, phi=40, lphi=150, shade=0.4)

#建立3-D图，如图1所示。3-D图展示平均气温对每日肺结核报告发病数的暴露—滞后—反应关系。crosspred()函数中，参数by=1是指计算所有整数平均气温的效应值。x轴为平均气温，y轴为滞后天数，z轴为RR值。

图1 不同滞后期不同气温对日发病数效应分布3-D图

P90<-as.numeric(quantile(Atemp,0.90))

crvar<-crossreduce(cb,model,type="var",value=P90,from=bound[1], to=bound[2],bylag=0.2)

plot(crvar,xlab="Lag",ylab="RR",col=2,lwd=2,tcl=0.5)

mtext(text=paste("Predictor-specific association at temperature ",P90, "℃",sep=""),cex=1)

#绘制特定平均气温时滞后—反应关系图，如图2所示。横坐标代表滞后天数，纵坐标代表RR值。滞后0 d时，平均气温第90百分位数(25.9 ℃)对日发病数的影响RR值小于1，随着滞后天数的增加RR值逐渐变大，滞后90 d时RR值大于1，但均无统计学意义。

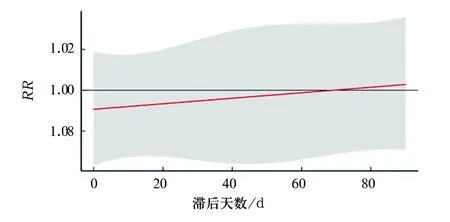
图2 平均气温第90百分位数(25.9 ℃)时对日发病数的滞后效应分布图

crlag <-crossreduce(cb,model,type="lag",value=90,from=bound[1],

to=bound[2],bylag=0.2)

plot(crlag,xlab="Tempeature/℃",ylab="RR",col=2,ylim=c(0.9,1.15),lwd=2,tcl=0.5)

mtext(text="Lag-specific association at lag 90",cex=1)

#绘制特定滞后时间时暴露—反应关系图，如图3所示。横坐标代表平均气温，纵坐标代表RR值。滞后90 d时，平均气温对日发病数影响效应无统计学意义。

图3 滞后90 d平均气温与日发病数的暴露—反应关系图

crall <-crossreduce(cb,model,from=bound[1],to=bound[2],by=0.2)

plot(crall,xlab="Tempeature/℃",ylab="RR",ylim=c(0,40),col=2,lwd=2,tcl=0.5)

mtext(text="Overall cumulative association",cex=1)

#绘制累积效应图，如图4所示。将每个滞后时间的滞后效应相加便得到累积滞后效应。不同平均气温对日发病数的累积效应不同，但均无统计学意义。

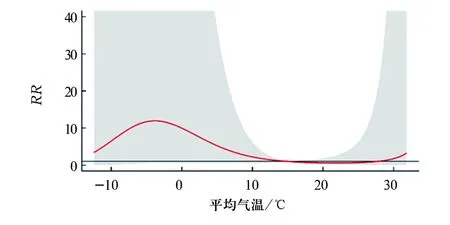
图4 不同平均气温对日发病数的累积90 d效应分布图

2.4 对各地级市进行模型建立

lag <-c(0,90)#滞后范围0～90 d

argvar <-list(df=3,fun="bs",cen=cen)#自变量与因变量的关系，自由度设置为3，基函数采用二次B样条函数，参考值采用平均气温的中位数；

arglag <-list(df=3,fun="ns")#参数arglag控制滞后效应，自由度设置为3，采用自然立方样条函数

yall<-matrix(NA,length(data),3,dimnames=list(regions,paste("b",seq(3),sep="")))

#将模型中估计得到的各地级市系数结果储存于yall矩阵中

Sall <-vector("list",length(data))

names(Sall)<-regions

#将模型中估计得到的各地级市的协方差结果储存于Sall矩阵中

fqaic <-function(model){

loglik <-sum(dpois(model$y,model$fitted.values,log=TRUE))

phi <-summary(model)$dispersion

qaic <--2*loglik + 2*summary(model)$df[3]*phi

return(qaic)}

#求Q-AIC值

system.time({

for(i in seq(data)){

sub <-data[[i]]

suppressWarnings({

cb <-crossbasis(sub$Atemp,lag=lag,argvar=argvar,arglag=arglag)

})#建立交叉基

mfirst<-glm(PTB～cb+ns(time,7*12)+DOW+Season+ns(SD,3)+ns(ARH,3)+ns(AWS,3)+ns(PRE,3),family = quasipoisson(),sub)#建立模型

suppressWarnings({

crall <-crossreduce(cb,mfirst)

})#对总体累积汇总

suppressWarnings({

crhot <-crossreduce(cb,mfirst,type="var",value=25.9)

})#对热效应汇总

suppressWarnings({

crcold <-crossreduce(cb,mfirst,type="var",value=-1)

})#对冷效应汇总

yall[i,]<-coef(crall)#整体模型系数

Sall[[i]]<-vcov(crall)#整体协方差

yhot[i,]<-coef(crhot)#热效应系数

Shot[[i]]<-vcov(crhot)#热效应协方差

ycold[i,]<-coef(crcold)#冷效应系数

Scold[[i]]<-vcov(crcold)#冷效应协方差

qaic[i]<-fqaic(mfirst)#求模型Q-AIC

}

})

#此为循环语句，对各地级市进行模型建立、提取模型系数以及协方差，为多元meta分析效应合并做铺垫。

2.5 进行多元meta分析

library(mvmeta)#加载mvmeta 包

method <-"reml" #选取随机效应模型，若用固定效应模型，采用“fixed”

mvall <-mvmeta(yall～1,Sall,method=method)#将各地级市整体结果进行合并

mvhot <-mvmeta(yhot～1,Shot,method=method)#将各地级市热效应结果进行合并

mvcold <-mvmeta(ycold～1,Scold,method=method)#将各地级市冷效应结果进行合并

m <-length(regions)#共有9个地级市

xvar <-seq(bound[1],bound[2],by=0.1)

bvar <-do.call("onebasis",c(list(x=xvar),attr(cb,"argvar")))

cpall <-crosspred(bvar,coef=coef(mvall),vcov=vcov(mvall),

model.link="log",by=0.1,from=bound[1],to=bound[2])

tperc <-seq(bound[1],bound[2],by=0.1)

bperc <-do.call("onebasis",c(list(x=tperc),attr(cb,"argvar")))

plot(cpall,type="n",ylab="RR",ylim=c(0,30),xlab="Temperature/℃",tcl=0.5)

for(i in seq(m)){

suppressWarnings(

lines(crosspred(bperc,coef=yall[i,],vcov=Sall[[i]],model.link="log"),

col=grey(0.8),lty=5)

)

}

lines(cpall,"overall",col=1,lwd=2)

abline(h=1)

lines(cpall,col=2,lwd=2)

mtext("Main model: first-stage and pooled estimates",cex=1)

legend("top",c("Pooled(with 95%CI)","First-stage region-specific"),

lty=c(1,2),lwd=1.5,col=c(2,grey(0.7)),bty="n",inset=0.1,cex=0.8)

#将所有地级市在各具体气温情况下的累计效应进行合并，绘制合并累积效应图，如图5所示。9个地级市平均气温对日发病数的合并累计效应先下降再上升，但无统计学意义。

图5 9个地级市平均气温对日发病数的累积效应分布图

round(with(cpall,cbind(allRRfit,allRRlow,allRRhigh)["10",]),3)#不同气温的累积效应

(qall <-qtest(mvall))#对整体合并进行Q检验

plot(cphot,type="n",ylab="RR",ylim=c(0.95,1.1),xlab="Lag",tcl=0.5)

xlag <-0:810/9

blag <-do.call("onebasis",c(list(x=xlag),attr(cb,"arglag")))

reghot <-apply(yhot,1,function(x)exp(blag%*%x))

matplot(xlag,reghot,type="l",col=grey(0.5),lty=2,add=T)

abline(h=1)

lines(cphot,col=2,lwd=2)

legend("top",c("Pooled(with 95%CI)","First-stage region-specific"),

lty=c(1,2),lwd=1.5,col=c(2,grey(0.7)),bty="n",inset=0.1,cex=0.8)

mtext(text=paste("Predictor-specific summary for temperature = ",25.9,

"℃",sep=""),cex=1)

#绘制9个地级市热效应合并图，如图6所示。9个地级市热效应对日发病数的滞后合并效应无统计学意义。

图6 热效应(平均气温25.9 ℃)时9个城市日发病数的滞后效应分布图

round(with(cphot,cbind(matRRfit,matRRlow,matRRhigh)["90",]),3)#在热效应时，不同滞后时间的效应

(qhot <-qtest(mvhot))#对热效应合并进行Q检验

plot(cpcold,type="n",ylab="RR",ylim=c(0.95,1.1),xlab="Lag",tcl=0.5)

xlag <-0:810/9

blag <-do.call("onebasis",c(list(x=xlag),attr(cb,"arglag")))

regcold <-apply(ycold,1,function(x)exp(blag%*%x))

matplot(xlag,regcold,type="l",col=grey(0.5),lty=2,add=T)

abline(h=1)

lines(cpcold,col=2,lwd=2)

legend("top",c("Pooled(with 95%CI)","First-stage region-specific"),

lty=c(1,2),lwd=1.5,col=c(2,grey(0.7)),bty="n",inset=0.1,cex=0.8)

mtext(text=paste("Predictor-specific summary for temperature = ",-1, "℃",sep=""),cex=1)

#绘制9个地级市冷效应合并图，如图7所示。滞后0～72 d冷效应对日发病数的效应无统计学意义，自72 d后，RR值大于1，具有统计学意义，冷效应是日发病数的危险因素。

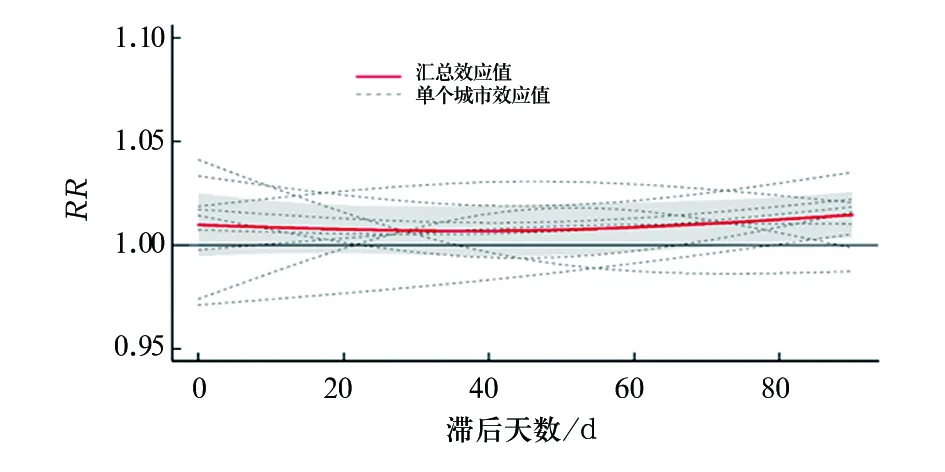
图7 冷效应(平均气温-1℃)时9个城市日发病数的滞后效应分布图

round(with(cpcold,cbind(matRRfit,matRRlow,matRRhigh)["90",]),3)#冷效应时，不同滞后时间的效应。

(qcold <-qtest(mvcold))#对冷效应合并进行Q检验

3 讨论

本研究结合实例，介绍了DLNM与多元meta分析在R软件中的实现过程。2阶段时间序列分析是环境流行病学中一个强有力的分析方法，在复杂关联的研究中提供了更大的灵活性且有更高的效率，可以减少选择性结果报告偏倚，并允许对各结果之间的关联进行建模，实现对结果的联合推断以及从一个结果预测另一个结果[8]。DLNM结合多元meta分析的2阶段分析，被国内外多项研究运用于气象因素、污染因素与疾病健康之间关系的研究[9-13]，与单一地区研究相比，将多个研究地区结果进行合并，可以减少研究的异质性，而且多元meta分析提供了更好统计特性的参数估计，特别是通过调整研究间协方差结构的估计，潜在地提高了研究结果的精度[7]。此外，利用R软件绘制各研究地点气象因素与疾病的暴露—反应曲线，以及合并后的曲线图，更加直观地探讨气象因素对疾病发病影响的非线性关系以及滞后效应。