气体放电管张弛振荡器的同步研究

耿梦乔，姜 旋，楼晨煊，庞清宇，白在桥，王爱记

(北京师范大学 物理学系，北京 100875)

同步是指多个动力学个体行为上的一致性，在自然界处处可见. 350多年前，惠更斯对于钟摆同步现象的探索，揭开了人们对同步现象研究的序幕[1]. 在物理领域，利用非线性电路的混沌同步来实现信号的加密；在生物领域，通过研究同步雌雄异熟来研究克隆植物的进化意义[2]；在医学领域，可以通过研究脑电图额-枕同步放电现象来研究癫痫问题[3]. 同步现象对于现实世界复杂系统集体行为的研究提供了新的范式，能帮助我们进一步理解复杂系统的功能是如何实现的，并根据同步原理设计具有新功能的系统；同时，同步现象有时也会造成不利影响，对同步的研究也可以规避这部分风险.

张弛振荡实验的实验装置是由RC充电电路[4]和气体放电管组成的非线性电路，可以实现气体放电管的张弛振荡. 以此为基础，用光敏电阻[5]代替原电路中的定值电阻，利用气体放电管的辉光放电特性与光敏电阻遇光电阻变小的特性，可以使得多个张弛振荡电路之间发生相互耦合，各电路的周期受到调制，在一定条件下可以实现周期同步[6].

本文首先在实验上观察到了上述同步现象，之后利用Mathematica软件进行数值模拟，对放电管同步的成因进行分析，并探究实验中影响气体放电管达成同步的条件.

1 实验原理

1.1 张弛振荡

气体放电管(简称为“放电管”)内含有惰性气体，可通过电极施加直流电压. 当放电管两端电压小于气体的击穿电压Uj时，里面的惰性气体不会被击穿，可以认为此时是断路；当放电管两端电压大于Uj时，气体发生辉光放电，此时放电管处于导通状态. 考虑在电源电动势为ε的RC充电电路中，电容两端的电压会逐渐升高，因此将放电管与RC充电电路的电容并联，如图1所示.

图1 张弛振荡电路图

当电容两端电压超过Uj时，放电管发生辉光放电，使电容放电；当放电管两端电压下降至稳定电压Ud后，放电管停止辉光放电. 辉光放电的持续时间t0通常很小可以认为是瞬间完成. 图1中的R0只影响放电管的放电速度，即影响放电时间t0，起到保护电阻的作用. 之后电容继续充电，

使得电压再次达到Uj，由此循环往复，形成张弛振荡现象.

放电管相邻2次辉光放电的时间间隔(简称为“振荡周期”)为

(1)

其中，R为电路中定值电阻的阻值，C为电容器的电容.

同时，可以定义周期差(表示2个放电管在独立运行时振荡周期之差的绝对值)

ΔT=|T1-T2|,

(2)

该周期差概念可以推广到多个电路.

1.2 放电管同步

放电管同步(简称为“同步”)是指2个或多个放电管在相互耦合之后振荡周期达到一致的现象. 本实验的目的是要通过设计新的张弛振荡电路，让周期差不为0的2个乃至多个放电管达到同步.

根据式(1)可知，放电管的振荡周期与电路中的电阻正相关. 如果电路中的电阻变化，那么放电管的振荡周期就会随之变化. 基于此思路，结合放电管的辉光放电特性，将定值电阻换成光敏电阻，形成新的张弛振荡电路.

设计2个张弛振荡电路——分别记为电路1和电路2. 将放电管1与光敏电阻R2置于暗室，放电管2与光敏电阻R1置于另一个暗室，且这2个暗室互不影响，如图2所示. 当放电管1发生辉光放电时，影响光敏电阻R2的阻值，进而影响放电管2的振荡周期. 同理，放电管2辉光放电也会影响放电管1的振荡周期. 经过2个电路之间的相互耦合，最终会使得2个放电管的振荡周期达到一致，即同步.

图2 2个耦合的张弛振荡电路的电路图

为了探究放电管同步的条件，需要解电路的微分方程. 假设当光敏电阻受到放电管影响时电阻瞬间下降到rmin. 显然，光敏电阻的阻值r=r(t)和放电管两端的电压u=u(t)均为分段函数. 根据该非线性电路的特点，可得到：

(3)

其中，R为电路中固定电阻的阻值，r为光敏电阻的阻值.

根据电路的性质可知，当u=Uj时，放电管发生辉光放电，之后u降到Ud，Uj和Ud是u(t)这一分段函数每一段端点的取值，该过程也会影响到另一个电路中光敏电阻阻值的变化. 因此，根据式(3)求解出u(t)的图像可以判断2个放电管是否达到同步，进而分析得到影响同步的因素.

2 实验及数值模拟结果

2.1 实验结果

式(3)中r只依赖于光敏电阻自身的性质. 取2个电路中的光敏电阻，测量这2个光敏电阻受到放电管辉光放电影响之后的伏安特性曲线，采集数据之后进行数据拟合.

利用示波器，可得到光敏电阻经过短暂光脉冲后，在电路中的分压随时间变化的曲线. 由于光敏电阻载流子的湮灭往往成指数变化,且实际情况中无法做到完全黑暗，因此光敏电阻存在最大暗电阻阻值，记为rmax. 基于此，给出经验公式

(4)

其中τ是光敏电阻的时间常量,Ti(i=0,1,2,…；T0=0)为光敏电阻受到光脉冲的时刻. 利用式(4)对所得数据进行拟合，拟合结果如图3所示.

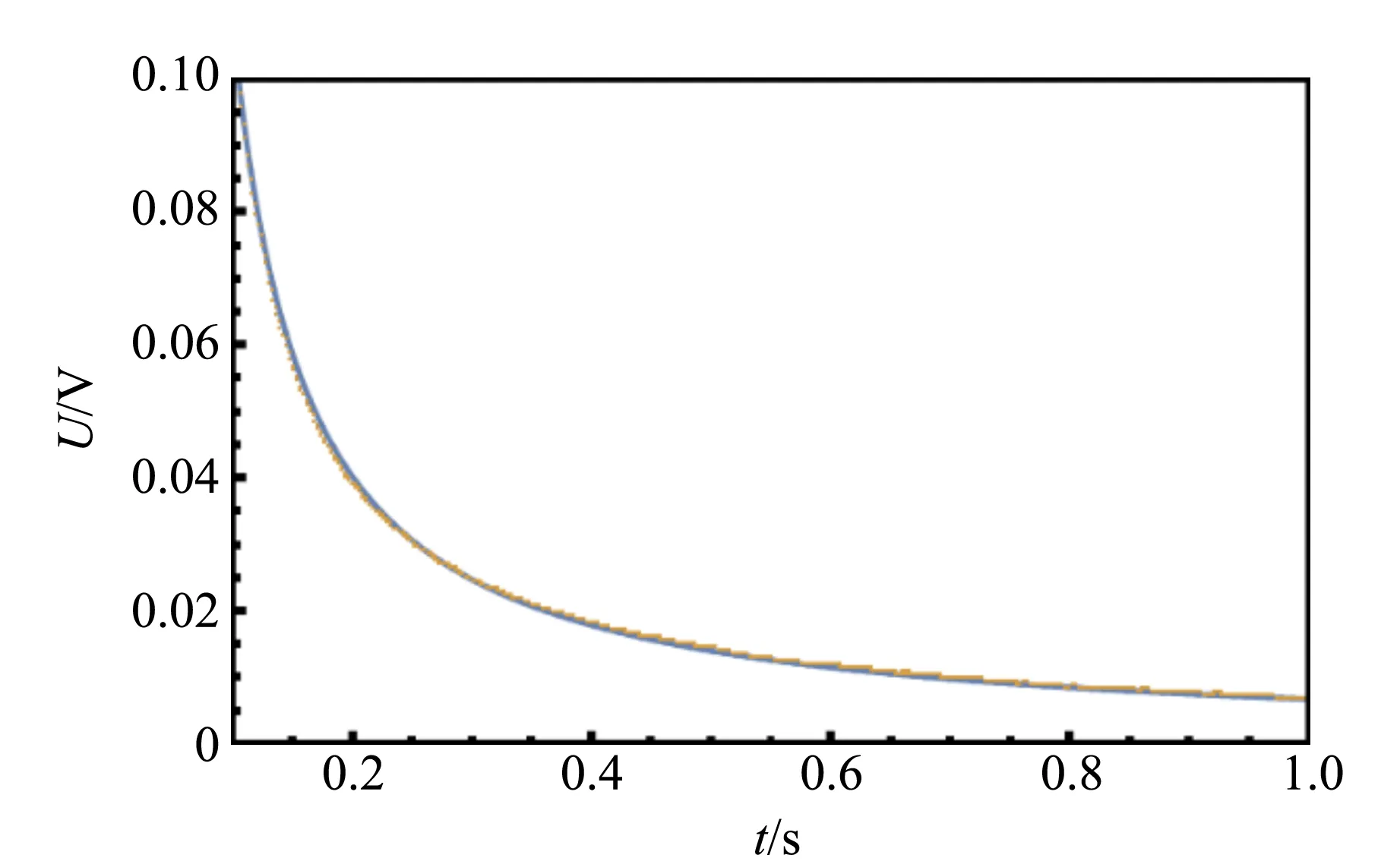
图3 拟合曲线与数据点对比图

为证实放电管的同步是否能实现，按照图2搭建实验电路，所用的电动势是最高300 V的可调电动势，电容均为1 μF，电阻均为10 MΩ. 为了使得2电路放电管周期可调，在2电路中串联电阻箱. 同时，2个电路均使用示波器测量定值电阻与光敏电阻串联之后的两端电压.

实验中，单独接通电路1，发现其周期为4.493 s. 之后通过调节电动势和电阻箱阻值来改变电路2的周期，最终发现当电路2周期为3.727 s时，2个电路达到同步(如图4所示)，同步周期为1.719 s. 在微调电路2的电阻箱后发现，虽然电路2的周期会微小改变，但1和2两电路在相互作用后仍能达到同步. 这说明，2个电路之间存在相互作用，且这种相互作用使得2个电路由原来的周期不一致达到同步，即在实验上验证了放电管的同步现象.

2.2 模拟结果

下面分析两电路耦合的系统，用下标k来代指电路1或2. 根据上文，电路k中的rk(t)和uk(t)满足式(3).

当电路k中的放电管在Tk，i+1时刻辉光放电后，该电路放电管两端的电压会从击穿电压Uk，j突变到稳定电压Uk,d，如图5中的标注所示，表达式为

(5)

同时，电路k′的光敏电阻阻值会受影响，满足式(4).

整理式(3)～(5)，得到如下方程组

(6)

其中k=1,2;k′=1,2;k≠k′. 式中的字母所代表的物理量和前文所述一致，仅用下标区别2个电路. 根据式(6),利用Mathematica软件画出u(t)的函数曲线，如图5所示.

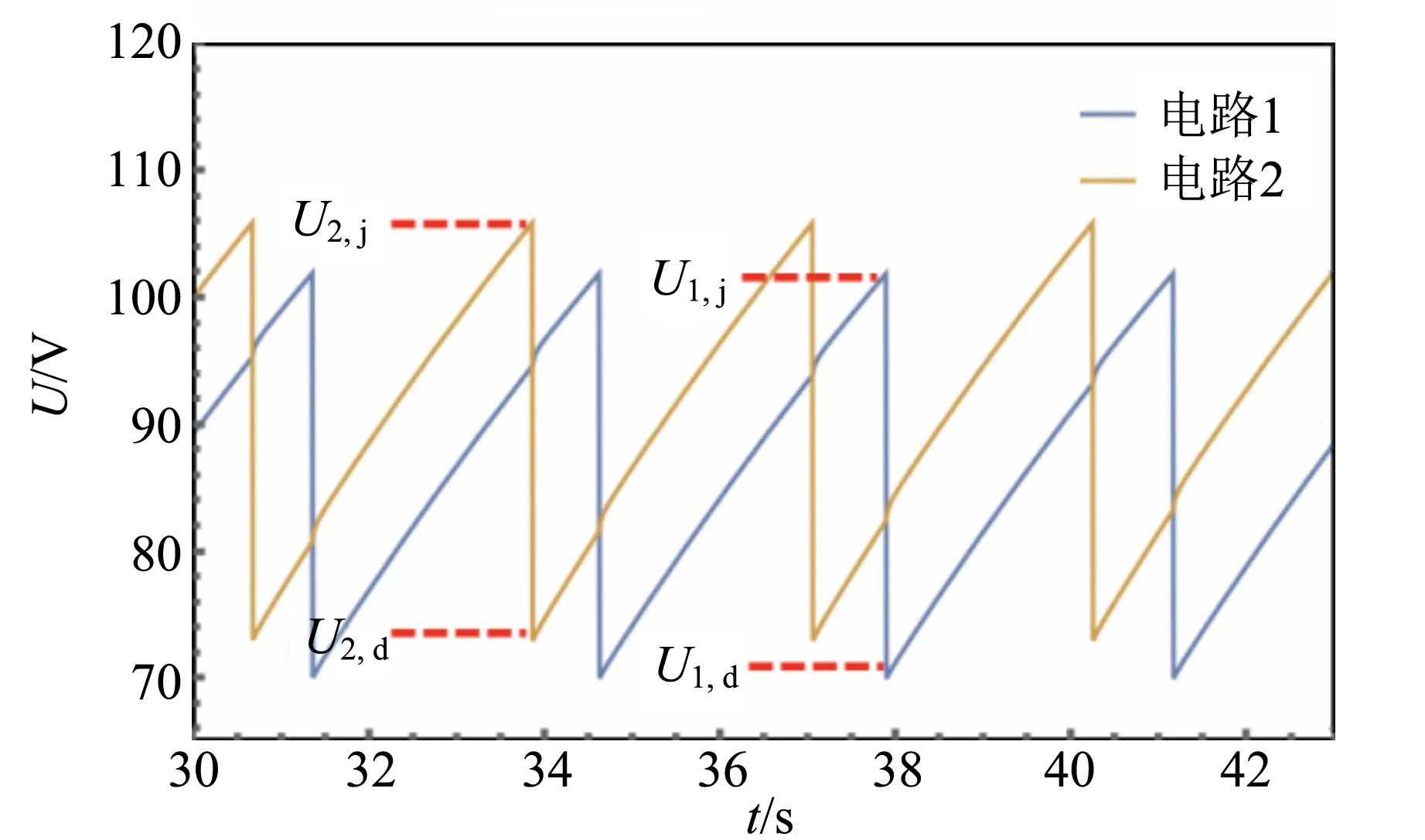
图5 未同步时两电路中电容两端电压随时间的变化

由于实际实验过程中，示波器测量的是两电路中定值电阻与光敏电阻两端的电压而非放电管两端的电压，二者曲线应关于u=0.5ε对称. 对比图4和图5可以看出，模拟曲线和实际曲线符合对称关系，说明模拟是合理的.

2.3 探究同步的影响因素

计算出u(t)的函数曲线之后，调节ε,R,C,Uj和Ud等参量，重复2.2，观察两电路振荡周期的相图，以此判断两电路是否同步.

由于在实际情况中，放电管的放电时间t0取值在50 ms左右，相比较振荡周期可忽略不计，所以在最开始的程序中忽略了这段时间，结果发现只有周期差为0的2个电路才能实现同步，且没有发现耦合过程，这显然与实际实验结果不符. 导致该结果的原因正是忽略了t0. 虽然t0相比振荡周期来说可以忽略，但光敏电阻的阻值变化不能被忽略，尤其是在电阻开始恢复的初期.

对图4中放电的过程进行分析，如图6所示. 绿线表示电路1的定值电阻与光敏电阻两端电压，黄线表示电路2的定值电阻与光敏电阻两端电压. 电路1的放电管在①处开始辉光放电，在②处结束；电路2的放电管在③处开始辉光放电，在④处结束. 从图4可以看出放电管辉光放电的时间与其振荡周期相比可以忽略，近似为1条竖直线. 但对于光敏电阻来说，这段时间不能被忽略.

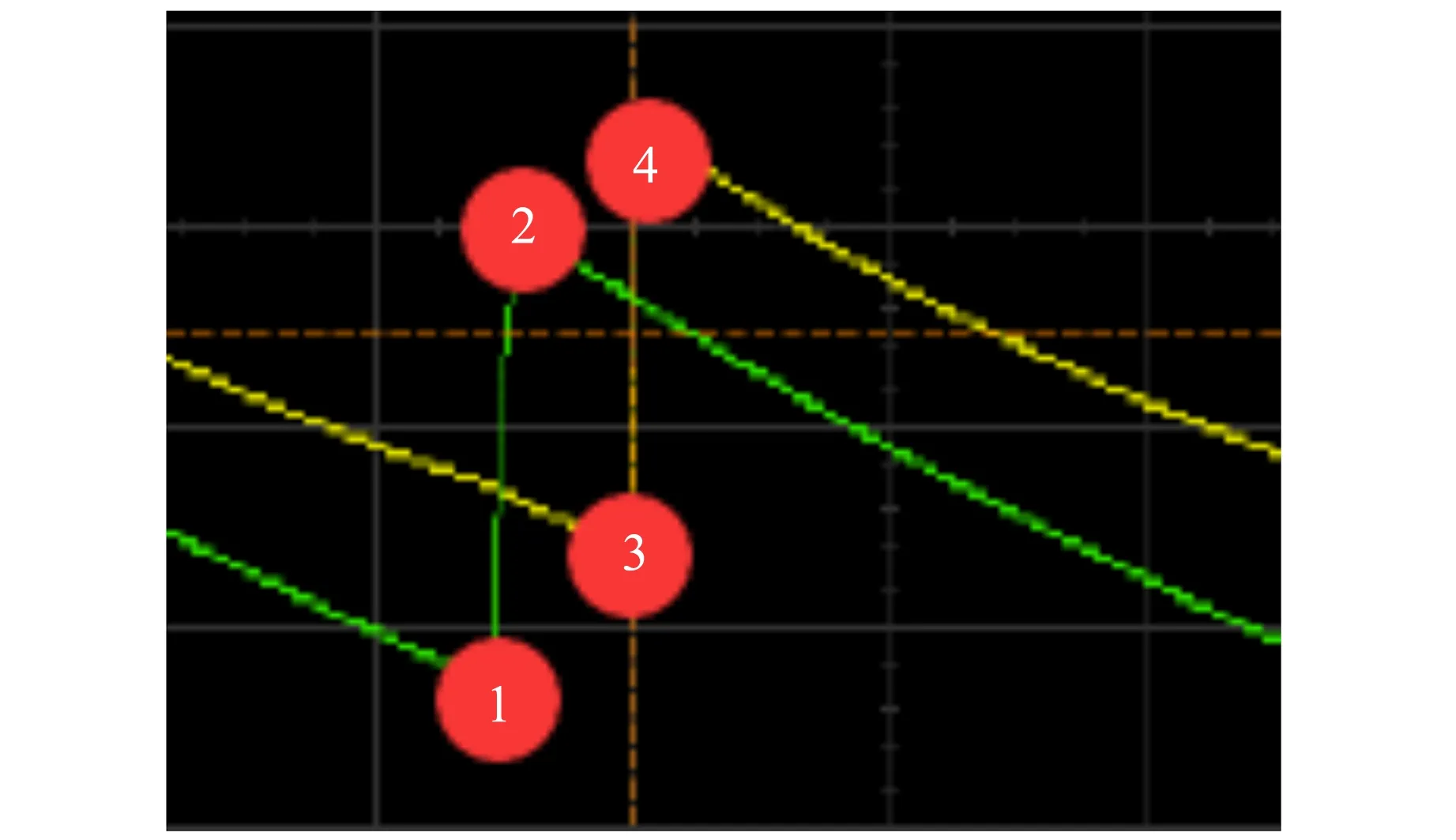
图6 放电管辉光放电的瞬间

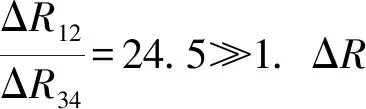
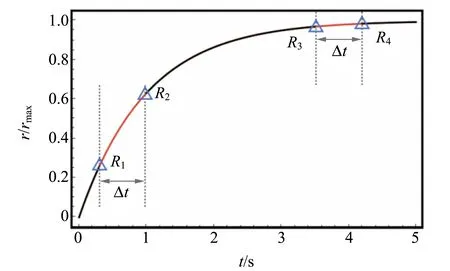
图7 电路1光敏电阻在辉光放电时间内的变化示意图

基于此，在原来程序的基础上增加条件：即当电路k(k=1，2)的放电管在t=Tk，i时放电，那电路k的光敏电阻阻值将从rk(Tk，i)突变为rk(Tk，i+t0)，这样既考虑到了放电管辉光放电的时间对光敏电阻阻值的影响，又在波形图上忽略了这段时间对振荡周期的影响.

在经过上述调整后，在程序上实现了周期差不为0的2个放电管的同步,如图8所示，说明t0是影响放电管能否同步的因素之一.

图8 改进程序后两电路的T-n曲线

图8中的n表示第n次辉光放电. 根据图8可以看出在前60次辉光放电的过程中存在相互调节的耦合过程，在60次之后两放电管达到同步. 显然，对于同个t0,2个放电管的周期差越小，越容易达到同步. 如果两放电管的周期差过大，就无法达到同步，如图9所示.

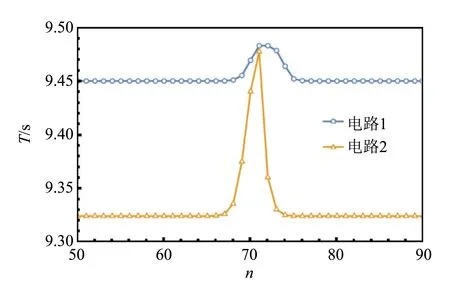
图9 周期差过大的两放电管未同步

考虑到光敏电阻τ越小，在t0的时间内阻值恢复得越快，因此τ也是影响放电管是否能同步的影响因素之一. 在图9所示的电路中调节τ，2个电路依旧可以同步，这就证明了这一猜想，其结果如图10所示.

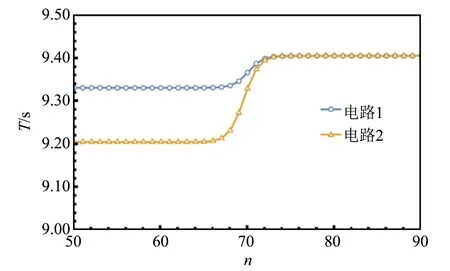
图10 调整τ后两放电管同步

同样，对于相同τ, 如果2个放电管的周期差过大，就无法达到同步. 因此，对于相同的t0和τ，存在极限周期差ΔT<ΔTmax,当两放电管的周期差小于ΔTmax时，两放电管可以达到同步，反之则不能达到同步. 因此，ΔTmax是决定2个放电管能否同步的决定性因素，而t0和τ正是通过影响ΔTmax来决定两放电管是否能达到同步.

根据进一步的模拟结果可以得出，ΔTmax与t0成正相关，但与τ的关系比较复杂，具体关系如图11所示.

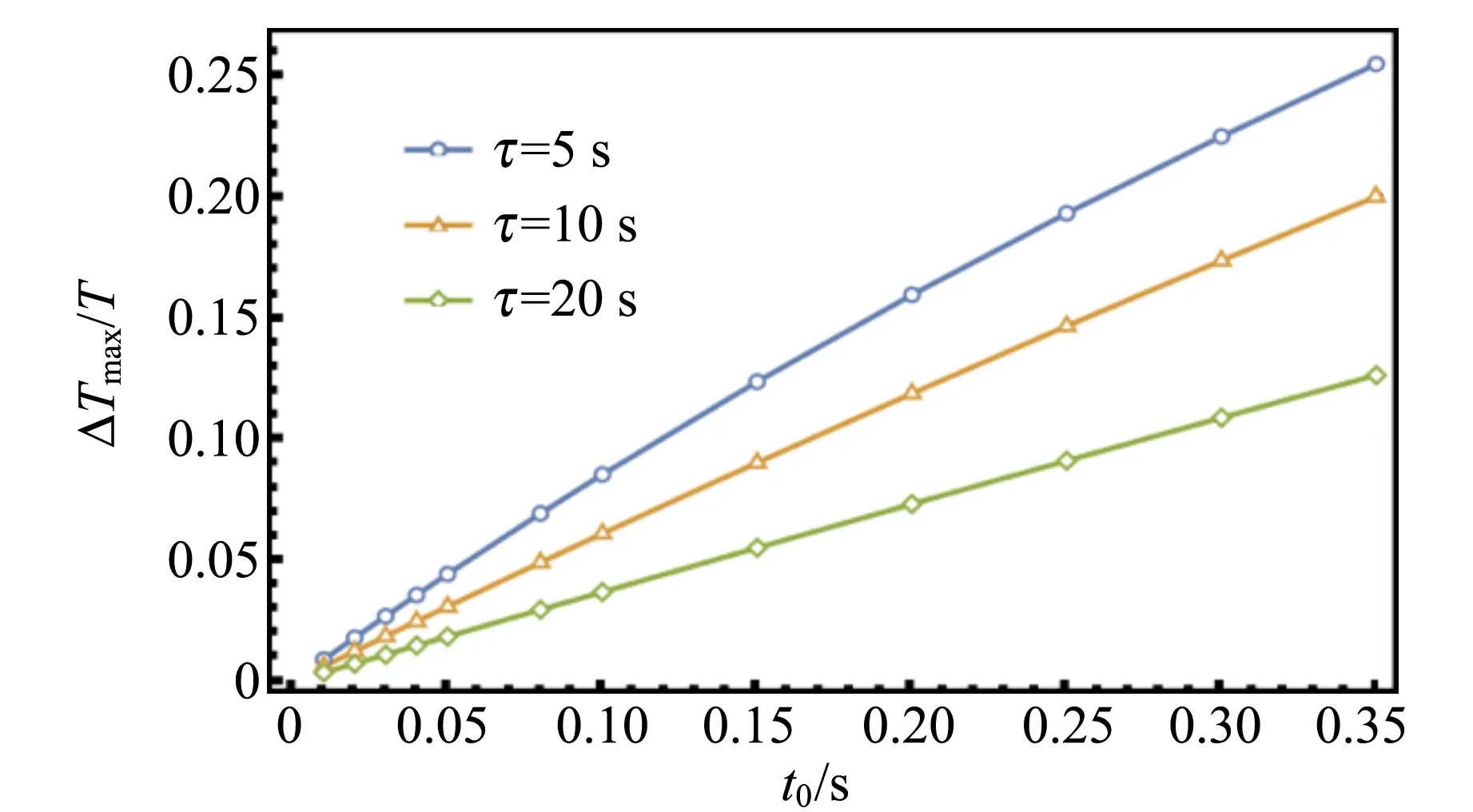
(a)

现定性地解释上述结果：

1)保持τ不变，ΔTmax与t0成正相关，随着t0的增大，t0对ΔTmax的影响减小.

2)保持t0不变，τ较小时，ΔTmax与τ成正相关；τ较大时，ΔTmax与τ成负相关

2.4 多电路模拟

现在将上述电路推广到3个电路，分别记为电路1,2和3. 现在令电路1的放电管影响电路2和3的光敏电阻，电路2的放电管影响电路1和电路3的光敏电阻，电路3的放电管影响电路1和电路2的光敏电阻. 经过模拟发现，在适宜的周期差下这3个放电管也能达到同步. 如图12所示，在30次辉光放电后，3个放电管达到同步.

图12 3个电路的放电管同步

理论上，该模型可以推广到n个电路，即第i个电路的放电管可以影响其他所有电路的光敏电阻，那么只要这n个放电管的周期差不太大，最终都会达到同步.

3 总结与展望

首先通过实验测量及数据拟合，验证了光敏电阻在受到光脉冲后，其阻值变化满足式(3). 在编写模拟程序时利用此结论得到了与实际相近的波形结果. 其次，探究了影响2张弛振荡电路能否同步的因素，并指出决定2个放电管是否能达到同步的3个因素：a.2个电路独立运行时的周期差ΔT;b.放电管辉光放电的持续时间t0;c.光敏电阻的时间常量τ.保持t0与τ不变时，需满足ΔT<ΔTmax，两电路方可同步. 经数值模拟发现，ΔTmax=ΔTmax(t0,τ)，且ΔTmax与t0正相关，与τ先是正相关之后是负相关关系，并对该现象进行了定性分析. 最后将该实验的模拟推广到多个电路，发现在多个电路中放电管的同步依旧可以实现.