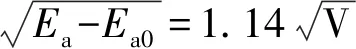冉绍尔-汤森效应实验的拓展研究

李明洋，马志远，张志华，关 佳，方 恺，赫 丽，沈 军

(同济大学 物理科学与工程学院，上海 200092)

物理学家冉绍尔与汤森在研究电子与气体原子的碰撞中，发现碰撞截面的大小与电子速度有关. 这种现象用经典物理无法解释，只能通过量子力学理论解释[1]. 为验证这种现象，利用电子碰撞管进行实验测量，通过加热灯丝产生热电子，并用加速电压加速，使电子与气体原子发生碰撞[2]，分别被屏极和板极吸收形成电流；通过在液氮温度和室温下进行实验，得到屏极和板极电流值随加速电压的变化关系，计算散射概率Ps和总有效散射截面Q，验证冉绍尔-汤森曲线. 同时做出几何因子f和板极电流IP随加速电压的变化曲线，进一步研究这种效应. 通过改变灯丝电压测定不同的冉绍尔-汤森曲线，探讨灯丝电压对曲线和几何因子f、板极电流IP的影响. 最后考虑到补偿电压的影响，探究了一种测量最佳补偿电压的方法.

1 实验原理

冉绍尔-汤森效应指电子散射概率和总有效散射截面与电子速度有关的现象，图1为几种惰性气体的冉绍尔-汤森曲线[3]，用加速电压平方根表示电子速度. 这种效应可以通过量子力学的分波带法求解电子在气体原子势场中的波函数进行解释. 要想更精确地计算散射概率，可采用Hartree-Fock自洽场方法[3-4]. 本文重点研究了电子散射概率与电子速度的关系图像，由于对散射概率的精确程度要求不高，因此采用测量散射电流占总电流的比值来表征电子散射概率.

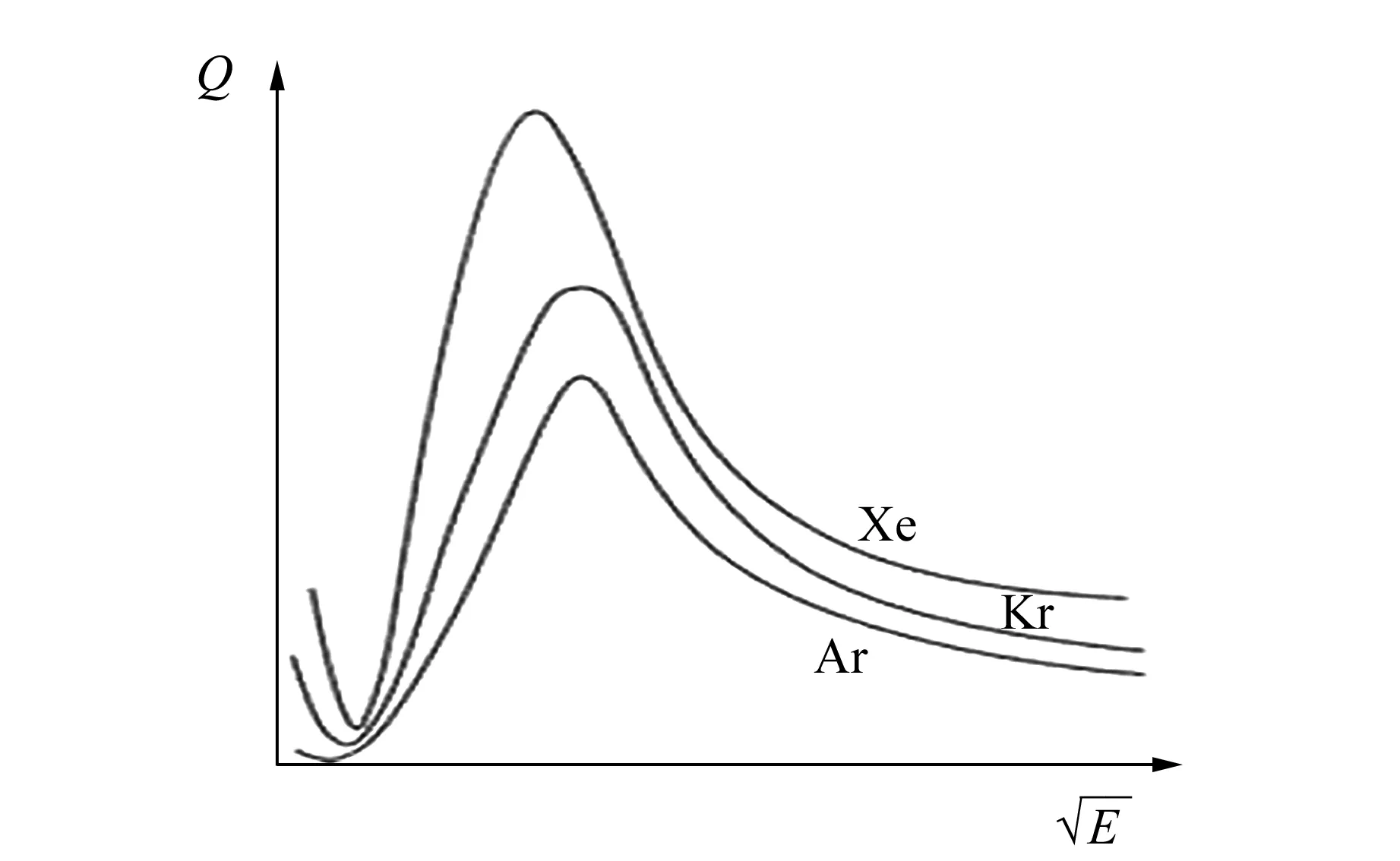
图1 惰性气体的冉绍尔-汤森曲线

充Xe电子碰撞管的结构示意图如图2所示. 屏极S为盒装结构，被1片开有矩形孔的隔板分成左右2个区域. 左面区域的一端装有圆柱形旁热式氧化物阴极K，内有螺旋式灯丝H(灯丝电压为EH)，阴极K与屏极S隔板之间有通道式栅极G，栅极与屏极连在一起形成加速极. 右面区域是等电位区，通过屏极隔板孔的电子与Xe原子在该区域进行弹性碰撞，该区内的板极P收集未能被散射的透射电子.

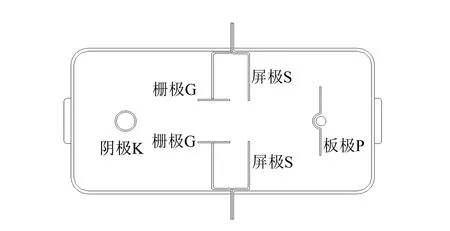
图2 充Xe电子碰撞管的结构示意图

图3为测量气体原子总散射截面的原理图[3]，当灯丝加热后，有电子自阴极K逸出，设阴极电流为IK，电子在加速电压Ea的作用下，一部分电子被屏极S接收，形成电流IS1；一部分电子穿越屏极S上的矩形孔，形成电流I0，其中Ec为补偿电压.

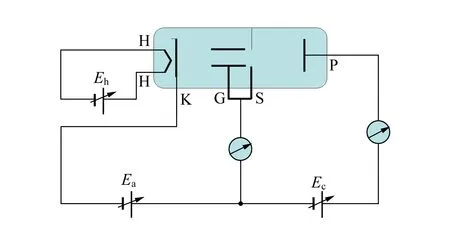
图3 测量气体原子总散射截面的原理图

由于屏极S上的矩形孔与板极P之间是等势空间，所以电子穿越矩形孔后以恒速运动. 受到Xe气体原子散射的电子到达屏极S，形成散射电流IS2；而未受到散射的电子则到达板极P，形成板极电流IP，因此有[3]

IK=I0+IS1,

(1)

IS=IS1+IS2,

(2)

I0=IP+IS2,

(3)

电子在等势区内的散射概率为

(4)

因此只要测量出IP和I0即可求得散射概率Ps. 其中IP可以直接测得，而I0则需要通过间接方法测定. 由于阴极电流IK分成2部分：IS1和I0，二者均与IK成比例，同时二者之间存在一定的比例关系，其比值称为几何因子[3],

(5)

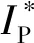
(6)

由于阴极电流与加速电压保持不变，因此有

(7)

另外，联立式(2)～(3)可得

(8)

代入式(7)，可得

(9)

故在实验中可通过式(9)来测量散射概率Ps.

电子总有效散射截面Q和散射概率Ps满足如下关系：

Ps=1-exp (-QL),

(10)

式中L为屏极隔离板矩形孔到板极之间的距离，对比式(9)和式(10)，得到

(11)

2 实验方法

在直流条件下通过精确测量验证冉绍尔-汤森曲线，按照图3连接电路图，液氮温度下调节补偿电压Ec，使IP和IS同时出现以确定Ec. 测量液氮和常温下IP，IS与加速电压Ea的关系，计算出散射概率Ps和总有效散射截面QL与加速电压的关系，验证冉绍尔-汤森曲线.

做出几何因子f随加速电压Ea的变化曲线，探究f与Ea的变化规律，同时做出板极电流IP随Ea的变化曲线，检验液氮温度下气体原子的散射是否可以忽略.

测量条件为：室温下灯丝电压EH=2.28 V，液氮下灯丝电压EH=2.00 V，补偿电压Ec=0.70 V. 初始加速电压Ea0=-0.30 V，逐渐增加至10.00 V. 为了节省测量时间且尽量不影响测量结果的精确度，在2.00 V以下每隔0.10 V记录1次数据，2.00～3.00 V每隔0.20 V记录1次数据，3.00～5.00 V每隔0.50 V记录1次数据，5.00～10.00 V每隔1.00 V记录1次数据.

改变灯丝电压EH，测量条件为：室温下EH=4.97 V，液氮下EH=4.30 V，Ec=0.40 V.Ea0=-0.90 V，逐渐增加至10 V. 测量不同灯丝电压下的冉绍尔-汤森曲线，进一步研究该效应的规律.

3 实验结果及讨论

3.1 验证冉绍尔-汤森效应

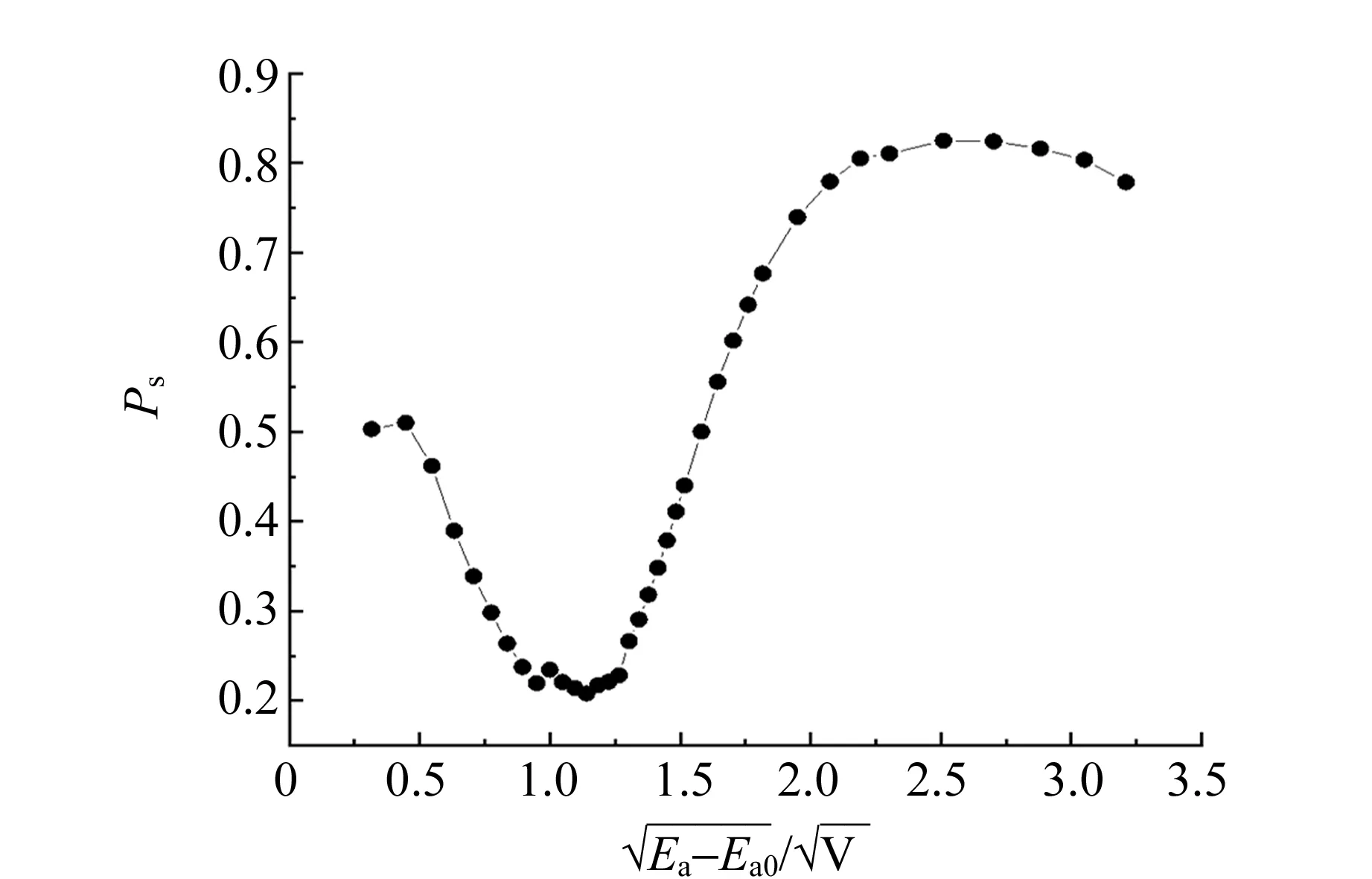
图4 低能电子散射概率Ps与关系

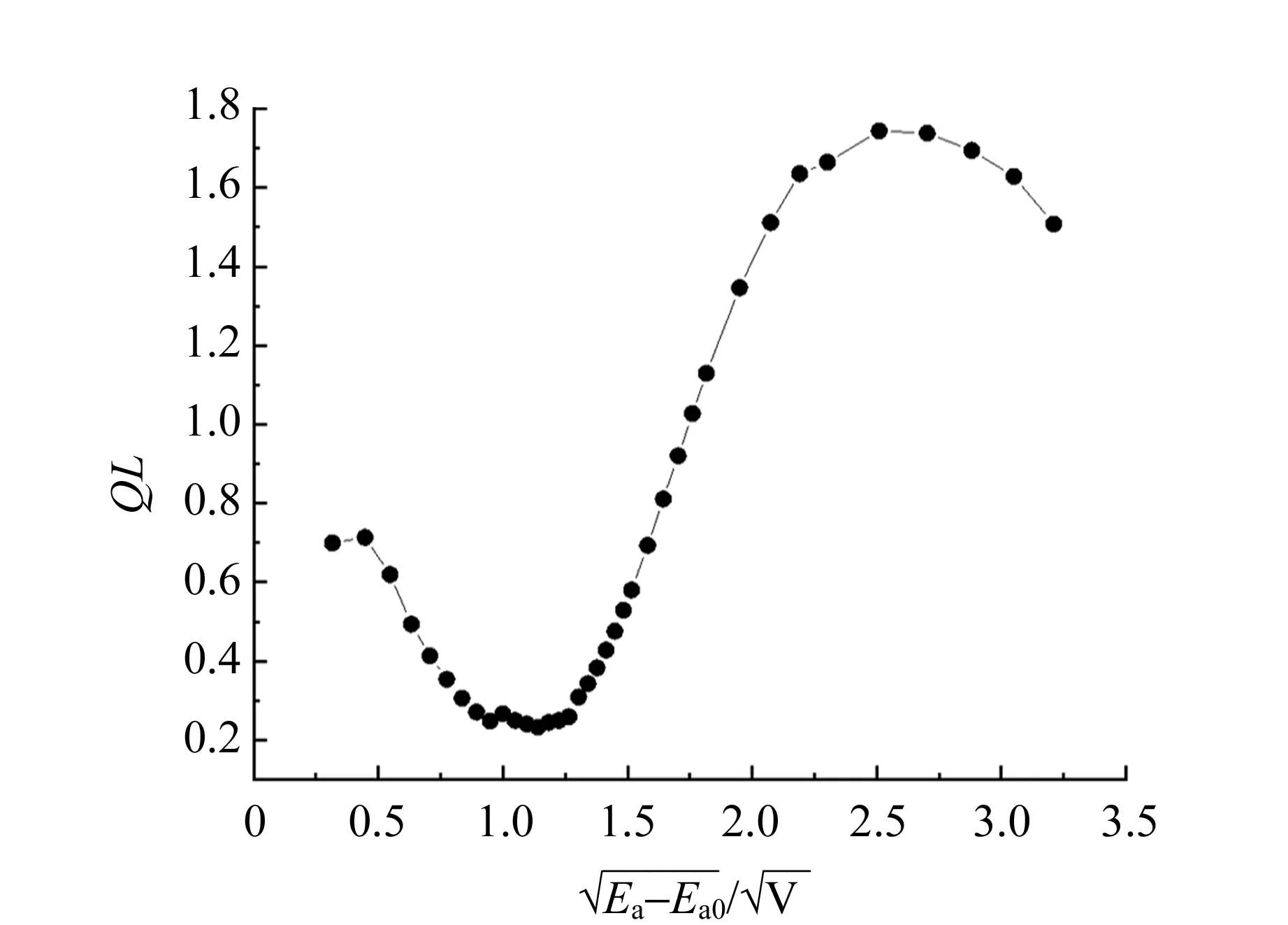
图5 总有效散射截面QL与关系

图6 几何因子f与关系

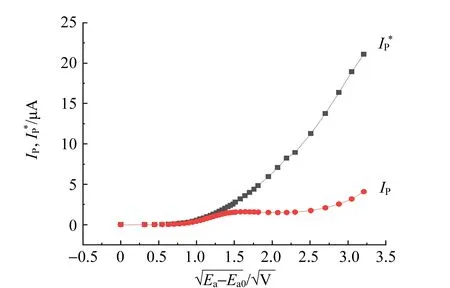
图7 板极电流IP与关系

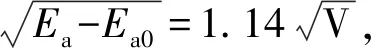
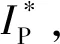
3.2 不同灯丝电压对电子散射概率的影响

图8 不同灯丝电压下Ps与的关系

图9 不同灯丝电压下QL与的曲线

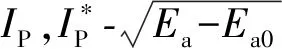
图10 板极电流与加速电压的关系

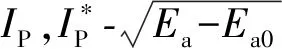
3.3 研究最佳补偿电压的测量方法

本实验中因考虑到栅极G与接收板极P间的散射，有接触电势差的存在，因此加补偿电压Ec消除其影响. 但实验中难以得到最佳补偿电压，若补偿电压偏小，冉绍尔-汤森曲线会向右平移，补偿电压偏大，冉绍尔-汤森曲线向左平移，如图11所示，这会导致测量电子对气体原子散射截面最小值的加速电压出现较大偏差[7].

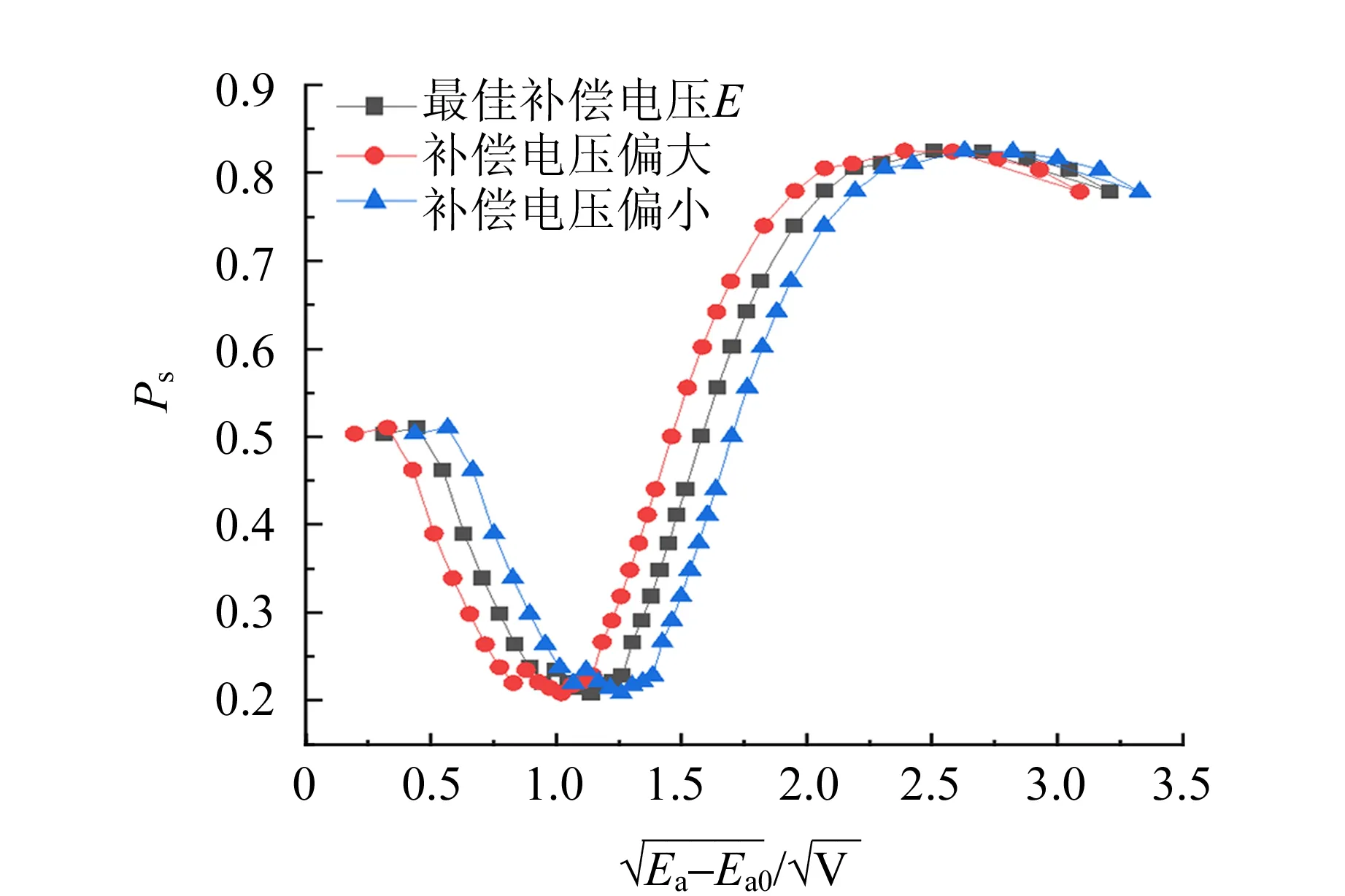
图11 补偿电压对冉绍尔-汤森曲线的影响

教材中测最佳补偿电压的方法是通过测得不同补偿电压下的冉绍尔-汤森曲线，并进行对比，得到最佳值. 这需测较多数据，且均为重复性测量，效率不高. 因此本文对实验进行了如下改进.

1)将加速电压调至Ea0，补偿电压调至比最佳补偿电压稍低的值(若不确定最佳补偿电压，可从较小值开始调节)，这时由于补偿电压并非最佳，导致冉绍尔-汤森曲线偏离标准曲线.

2)测量该补偿电压下液氮与室温环境下的IP，IS，求出散射概率Ps.

3)不断增加补偿电压的值，求出散射概率PS，直到补偿电压高于最佳值.

4)画出Ps-Ec曲线，理论上曲线先下降后上升，存在最小值，而Ec的最小值对应的补偿电压即为最佳补偿电压. 这是因为随着补偿电压增加，冉绍尔-汤森曲线由右向左移动，与标准曲线重合时Ps最小.

4 结 论