基于线偏振光测量液体折射率与反射率的研究
姚星星,刘书悉,厉位阳
(浙江大学 物理学系,浙江 杭州 310013)
折射率是介质光学特性的重要参量,通过折射率可以了解物质的光学性能、纯度、浓度以及色散等[1]. 物理实验中测量介质折射率的方法较多,如最小偏向角法、布儒斯特角法、干涉法及椭偏仪法等[2]. 其中较为常用的是分光计实验中的最小偏向角法和光的偏振实验中的布儒斯特角法[3-5]. 干涉法利用相干光形成薄膜等厚干涉条纹的原理来确定薄膜厚度和折射率[6]. 椭偏仪法是利用椭圆偏振光入射样品表面,通过检测和分析入射光和反射光的偏振状态,获得薄膜厚度及折射率的非接触测量方法[7]. 本文首先通过对称变换法确定出偏振方向,再利用非线性拟合法得到溶液的折射率. 运用理论和实验研究了溶质质量分数如何影响折射率,并测量出混合溶液折射率与各组分质量分数之间的线性叠加关系. 该装置和方法不仅可以测量溶液,也能测量镀膜材料的光学性质,且具有实验光路调节简单、数据处理简便、精确度高等优点.
1 实验原理
1.1 对称变换法确定偏振片的特征方向
在光具座上插上激光器和偏振片(带刻度盘),在右端测量偏振光通过偏振片后产生的光电流,如图1所示. 现要测定光源和偏振片的偏振角度,即光源偏振方向与竖直方向的夹角ψ,以及当偏振片偏振方向处在竖直方向时,刻度盘指针的读数φ.

图1 偏振片特征方向确定实验原理图
为后续表述方便,规定-90°<ψ,φ≤90°,当角度为负数时,表示从竖直方向逆时针(正视偏振片刻度盘视角来定义)转动锐角达到待测方向;当角度为正数时,表示顺时针转动锐角达到待测方向.
调节偏振片偏振方向,使万用表电流读数达到最大,记录刻度盘指针所指角度θ1(0°≤θ1<360°);转动偏振片所在的支架180°,使偏振片的另一面正对光源,顺时针旋转偏振片,使万用表读数再次达到最大,记录指针所指角度θ2(0°≤θ2-θ1<180°). 下面分情况讨论:
1)若ψ<0(逆时针偏转),如图2(a)所示,激光偏振方向原为1,偏振片转动180°后,激光偏振方向在刻度盘上的位置关于竖直轴对称变换到1′,故偏振片需要旋转的角度为
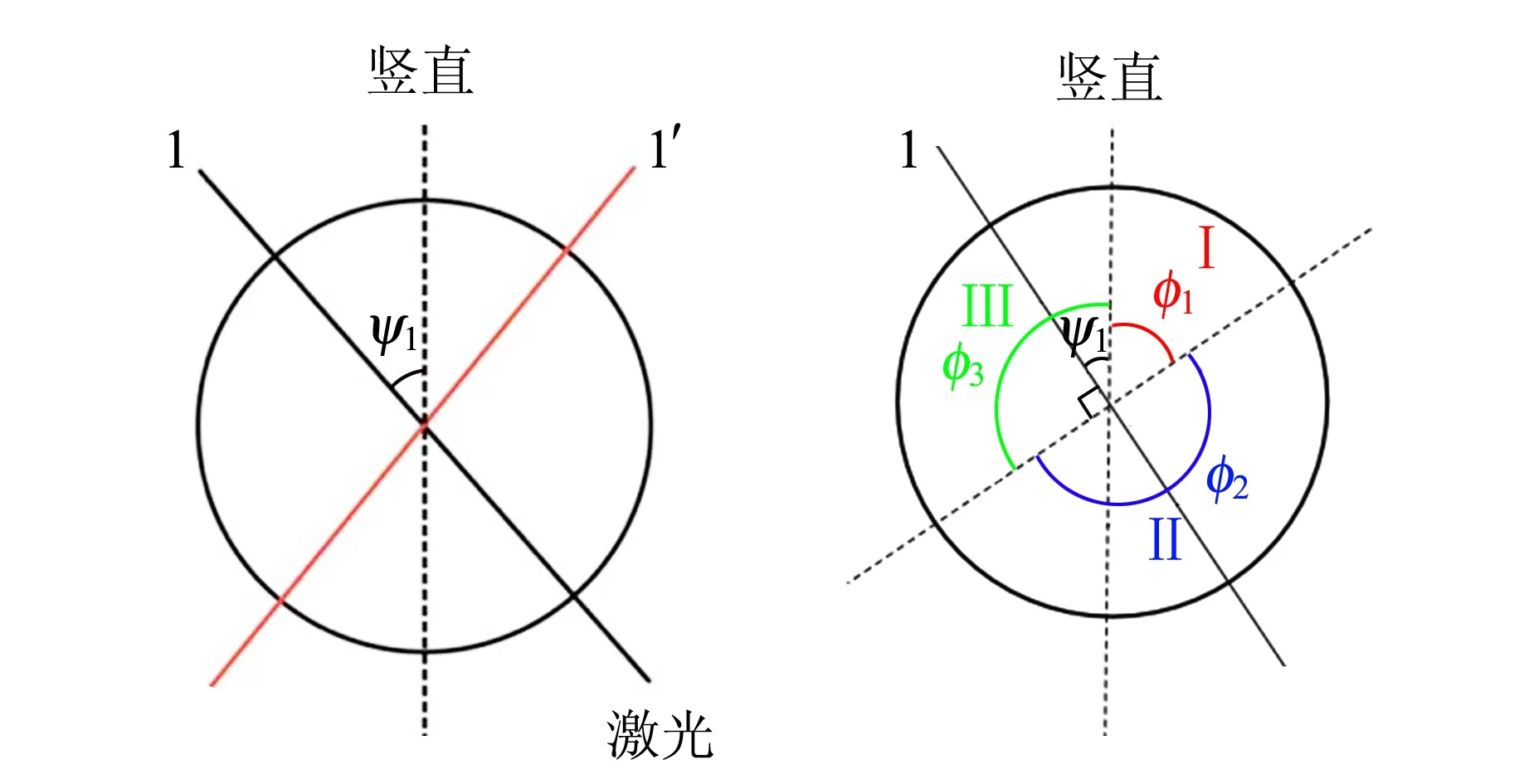
(a) (b)图2 激光光路示意图1
(1)
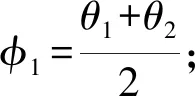
2)若ψ>0(顺时针偏转),如图3(a)所示,激光偏振方向由2变为2′,偏振片需要旋转角度

(a) (b)图3 激光光路示意图2
(2)
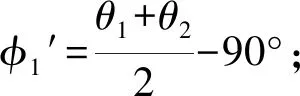
根据规定(-90°<φ≤90°),刻度盘指针读数表示为
(3)
显然,每次测量都会得到2个不同的φ值,2个值符号相反,差为90°,分别对应着偏振方向和与偏振方向垂直的方向(统称特征方向). 至于哪个方向为偏振方向,还需要通过其他方法进一步确定.
1.2 反射曲线拟合法测定折射率
光在界面上的光路示意图如图4所示,根据菲涅耳公式,光经介质分界面反射后,入射光和反射光的电矢量s,p分量满足以下关系:

图4 光在界面上的光路示意图
(4)
因此,光强反射率为
(5)
若从空气入射介质,n1=1,sini1=n2sini2,线偏振光在各个入射角下的反射率就由介质的折射率n2确定,将其代入式(5)可以得到反射率与入射角的关系为
(6)
由式(6)可知,通过测量出不同入射角i1下的p方向偏振光(简称p光)或s方向偏振光(简称s光)的反射率Rp或Rs,就可以进行拟合得到介质的折射率n2.
p光和s光的反射率曲线具有显著不同的特征,如图5所示. s光的反射率随入射角单调递增,而p光存在反射率为0的极小值点,该点对应的入射角为布儒斯特角.

图5 s,p光的反射率曲线
1.3 离子溶液折射率与溶质质量分数的关系
若入射光的光强不足够强,则粒子相对于平衡位置的偏移量r很小,假设溶液中粒子间的相互作用是弹性的,且运动阻力与其速度成正比. 设固有频率为ω0,质量为m,阻力系数为mγ,带电量为q的粒子在电矢量E作用下的运动方程可以表示为
(7)
稳定时,系统将以驱动频率振动,即
r(t)=r0e-iωt.
(8)
将式(8)代入式(7)解得:
(9)
其位移极化部分的电偶极矩为
(10)
假设在溶液中存在j种离子,其单位体积内的粒子数为Nj,固有频率为ωj,则位移极化部分的极化强度为
(11)

(12)

(13)
这表明在一定浓度范围内,离子溶液对单色光的折射率和离子浓度间具有线性关系.
2 实验器材与内容
2.1 实验器材
实验器材:半导体激光器(波长约650 nm)、S3590-082F-12型硅光电池、VC9805A型万用电表、带刻度盘的旋转盘、偏振膜、自制反射测角仪、载物支架、电子天平、量筒、透明容器、烧杯、NaCl晶体、Na2CO3固体、色素、纯净水、螺钉、六角螺丝刀、固体胶.
自制反射测角仪主体由半圆形有机玻璃刻度盘和底盘拼合而成,刻度盘标示角度范围为0~180°,分度值为1°,游标盘精度为0.1°. 底盘上可插入光学器件,并配有固定螺钉,水平放倒时可作为简易的短光具座使用,如图6所示.

(a)示意图
2.2 实验内容
2.2.1 偏振片特征方向的确定
具体操作步骤:
1)固定激光器,水平放倒反射测角仪.
2)滑动支架1和支架2到测角仪底盘左右两侧,在两支架之间插入带刻度盘的偏振片,调节激光器、偏振片和硅光电池探测器为等高共轴.
3)旋转偏振片使光电流达到最大,记录此时指针所指刻度θ1.
4)转动偏振片所在支架180°,使偏振片的另一面正对光源,顺时针旋转偏振片使万用表读数再次达到最大,记录指针所指角度θ2(θ2≥θ1).
5)旋转激光器,重复测量6次,由式(3)计算出特征方向φ,结果如表1所示.

表1 激光特征方向的测量
经计算,得到偏振片的2个特征角度分别为:负值特征角度φ1=-19.1°±0.4°,正值特征角度φ2=70.9°±0.4°.
2.2.2 s/p光的制作和离子溶液折射率的测量
具体操作步骤:
1)转动偏振片使指针指向特征角度φ1,此时竖直方向和水平方向均为偏振片的特征方向.
2)转动激光器使光电流达到最大,此时激光偏振方向为竖直或水平方向,并分别垂直或平行于半圆形刻度盘(即入射面). 由此,制作出s光或p光.
3)竖立反射测角仪,移动2个载物支架调节入射角i1=40°,调节待测溶液液面高度使反射光点落在光电池中心.
4)记录光电流和遮挡激光后的背景光电流. 每次按步长为0.5°或1°增大i1,测量光电池的光电流和背景光电流. 直到反射角i1′=65°,绘制反射率曲线.
若绘制出的反射率曲线单调递增,表明得到的偏振光是s光,则φ1为偏振片的偏振角度. 反之,得到的偏振光就是p光,即φ2为偏振片的偏振角度.
2.2.3 探究溶液颜色对偏振光反射率的影响
分别制作s光和p光,测量待测有色溶液的反射率曲线. 操作方法和步骤与2.2.2相同. 改变有色溶液的颜色,测量其反射率曲线,分析实验数据反映出的规律.
3 实验结果与讨论
3.1 离子溶液折射率与浓度的关系
通过2.2.2中的操作步骤得到偏振片的偏振角度为φ=φ2=70.9°±0.4°,即得到p光. 再利用p光下的反射率曲线,依据式(13)拟合得到待测液体折射率n. 换用不同质量分数、种类的离子溶液或混合溶液,测量其折射率,研究折射率与质量分数之间的关系,实验结果如表2所示.
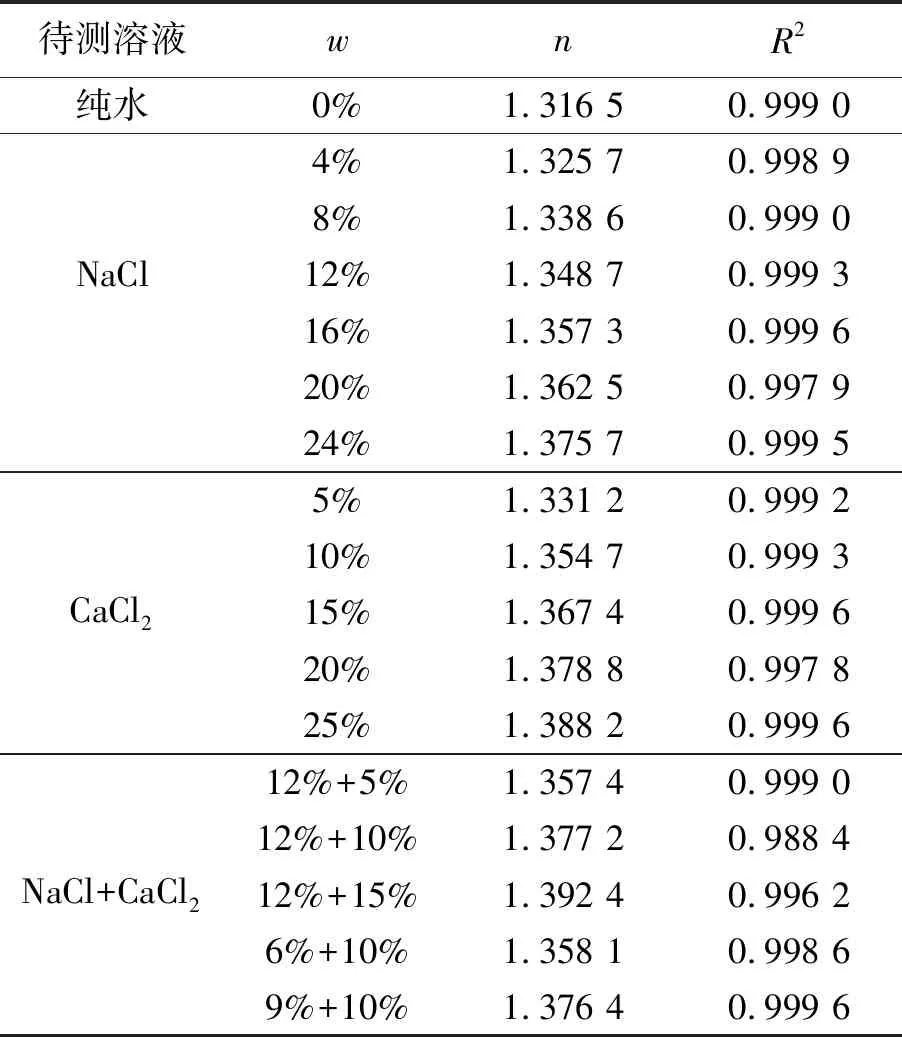
表2 不同种类、质量分数的溶液拟合得到的折射率
进一步分析离子溶液的质量分数与折射率的关系,绘制表2中不同质量分数w的NaCl溶液和CaCl2溶液的折射率n的关系图,得到质量分数与折射率的线性关系,如图7所示.
由于该2种溶液混合不发生化学反应,根据理论分析,离子溶液的折射率与离子浓度成正比,因此,二者的混合溶液的折射率与各成分的质量分数之间均呈现线性关系,即
nmix≈0.238wNaCl+0.292wCaCl2+1.319.
(14)

(a)NaCl溶液
利用几种混合溶液的测量结果对上式进行验证,如表3所示. 由表3可知实验测量值与理论值的相对偏差均在±0.5%以内,表明实验结果与理论分析基本吻合.

表3 混合溶液折射率的测量值与理论值
3.2 有色溶液反射率与颜色的关系
由于反射法测量只依赖于液体的表层反射,对于很薄的液体层,吸收率可忽略不计. 因此,对于质量分数均为10%的有色溶液(存在光的吸收),s/p光的反射率曲线仍然与菲涅耳公式拟合出的曲线符合较好(R2>0.998),如图8所示. 当入射角i1<53°时,黑色、蓝色溶液对p光的反射率R高于红色溶液,如图8(a)所示;而对于任意入射角,黑色、蓝色溶液对s光的反射率R均高于红色溶液,如图8(b)所示. 虽然有色溶液中的食用色素成分均为有机物,但可以发现无论用p光还是s光照射,根据反射曲线拟合得到相同质量分数的有色溶液折射率满足关系:n胭脂红色 (a)p光 对于出现以上现象的原因可以借用位移极化的机理进行解释:无极分子发生位移极化和有极分子发生取向极化时,均要从电场中获得能量,用于补偿振动过程中的能量损耗. 溶液呈现红色的原因是分子对红色波长的光吸收较少,因此用红色激光照射时,分子仅能获得少部分的光能用于极化振动,即极化强度越小,折射率也越小. 采用非线性拟合法测量溶液的折射率不仅克服了布儒斯特角附近光强较小、难以准确界定的缺陷,还有效利用了实验数据,提高了折射率的测量精度. 另外,提出了确定偏振片特征方向的简单方法——对称变换法,该方法思想巧妙,操作简单,具有较高的精确度,再配合反射率曲线,最终能够确定出偏振片的偏振方向. 本文在理论和实验上研究了溶液质量分数对折射率的影响,并测量出了混合溶液折射率与各组分浓度之间的线性叠加关系. 该实验对折射率的测量不依赖于折射光,因此适合用于测量有色溶液的折射率. 溶液折射率与离子质量分数的关系研究为测量(混合)溶液中的离子质量分数提供了可行思路.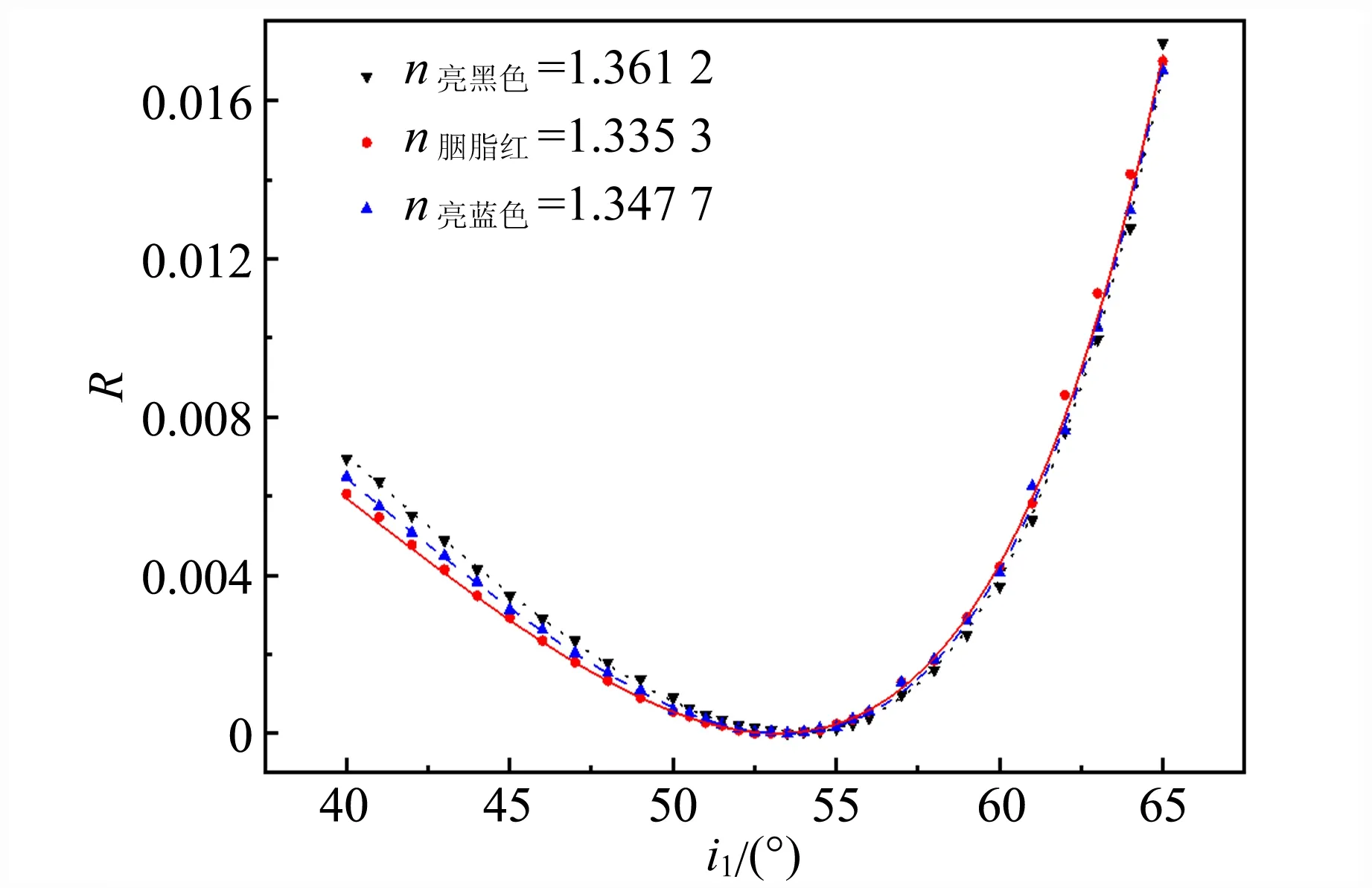
4 结束语

