低气压射频等离子体的探针诊断方法

刘永新，张莹莹

(大连理工大学 物理学院 基础物理国家级实验教学示范中心，辽宁 大连 116024)

射频等离子体技术已经广泛应用于集成电路制造、光伏产业、平板显示等领域中的材料刻蚀、薄膜沉积、表面清洗、离子注入等工艺中[1]. 目前，我国微电子企业外购芯片面临诸多困境，生产具有自主知识产权的高端刻蚀机成为物理、微电子等学科关注的焦点. 在芯片加工制造过程中，有接近1/3的工序需要借助等离子体处理技术完成. 低气压射频等离子体主要用于反应性离子刻蚀工艺，其最大优势是可以产生大面积、均匀的等离子体，从而在一定程度上保证基片表面刻蚀的均匀性. 因此，在本科实验教学中，有必要使学生了解国家重大战略需求，使学生认识到我国在低气压射频等离子体物理相关领域的研究进展和技术瓶颈，培养学生探索研究的兴趣，为国家输送相关后备人才.

1 原 理

在低温等离子体技术中，等离子体化学反应不需要较高的温度. 这类等离子体中电子密度在108～1012cm-3范围，电子温度在1～10 eV的范围内. 根据反应器的形状及电源耦合方式的不同，射频等离子体可以分成感性耦合等离子体、容性耦合等离子体以及螺旋波等离子体. 各类射频等离子体的诊断方式与方法相似，本文以容性耦合等离子体(Capacitively coupled plasma，CCP)的探针诊断为例进行介绍.

射频容性耦合等离子体由真空腔室构成，其结构示意图如图1所示. 腔室中包含1对平行的金属电极板，间距为1～10 cm，其中1个电极板由射频电源驱动，另1个电极可以接地，或者接入射频电源，从而实现双频电源同时驱动. 如果不采用介质(例如陶瓷)套筒对平行板之间的等离子体进行约束，则接地的腔室侧壁将构成容性耦合等离子体的第3个电极.

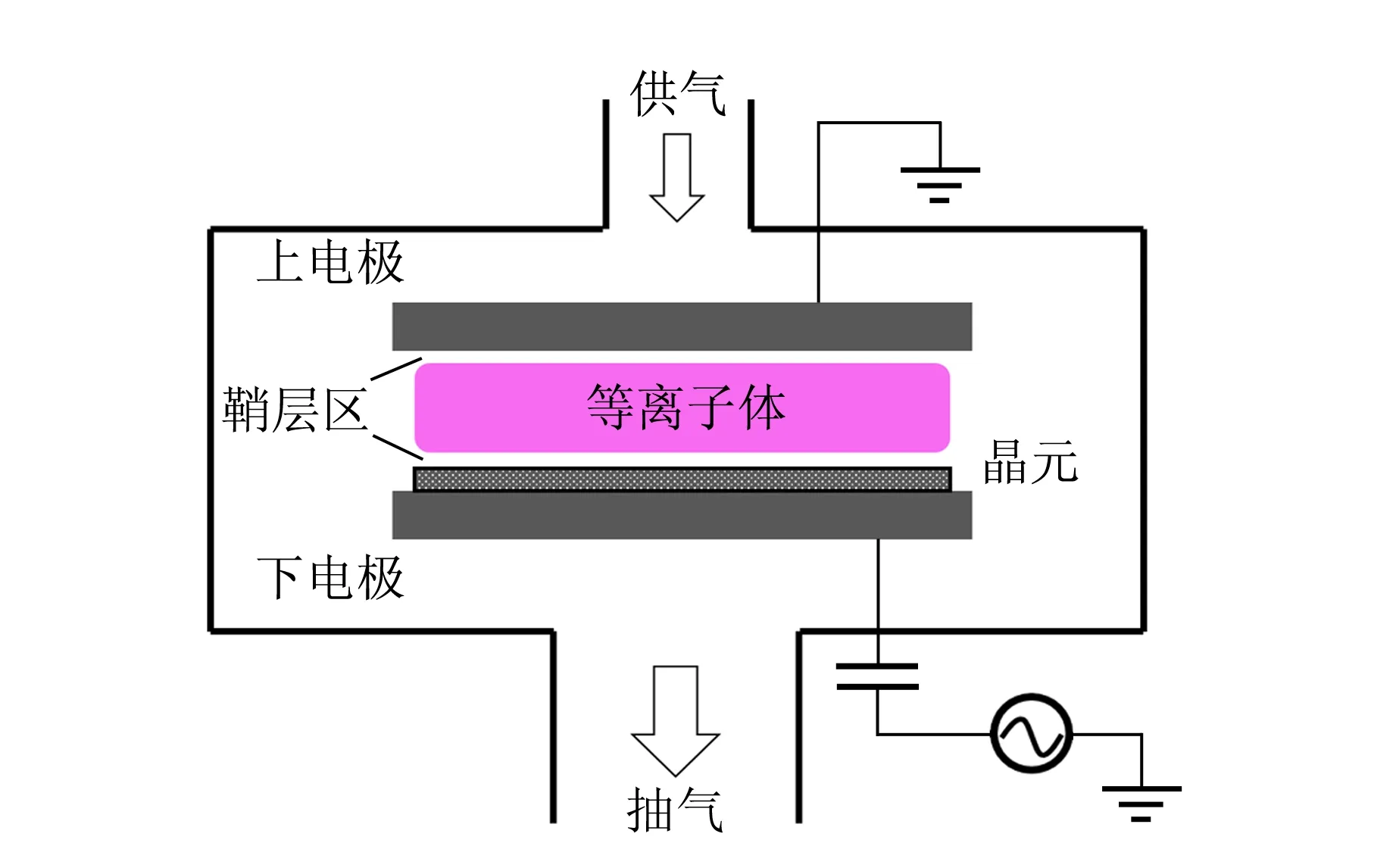
图1 射频容性耦合等离子体腔室结构示意图

典型的射频驱动电压在0～103V之间，对于某些介质深刻蚀工艺，射频电压可以达到104V. 工作气体通过“淋喷头”式的电极表面流经放电区域，残余气体被真空泵系统抽出. 容性放电是典型的“三明治”(鞘层—等离子体—鞘层)结构. 质量较小的电子能够响应射频电场，在以正离子为背景的两电极之间振荡. 靠近电极的区域是空间正电荷的鞘层区，鞘层中有很强的静电场，方向由等离子体区指向电极表面. 鞘层电场在一定程度上能限制电子，加速正离子轰击电极板. 对于CCP，用于介质刻蚀时，工作气压在10～100 mTorr(1 mTorr=0.133 322 Pa)之间，驱动频率普遍采用60 MHz，等离子体密度在109～1011cm-3之间；用于薄膜沉积时，工作气压较高(1 Torr量级)，电源频率一般采用13.56 MHz.

射频等离子体的实验研究进展取决于诊断手段的发展水平，因此采用多种诊断方式，可以从测量等离子体的多个状态参量入手，加深对等离子体性质的理解. 例如，静电朗缪尔探针可以测量惰性气体等离子体中电子能量分布函数、电子密度等；微波共振探针可以测量反应性气体放电中的电子密度；磁探针可以测量等离子体中磁场强度，进而计算电流及功率等. 下面介绍几种典型探针的结构、工作原理及测量结果.

2 探针诊断方法

2.1 朗缪尔探针

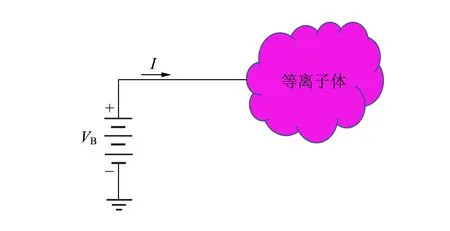
20世纪20年代，朗缪尔(Langmuir)发明了用于诊断等离子体的探针，并同Mott-Smith一起对其进行了详细地分析，这种探针被称为朗缪尔探针[1]. 由于该探针结构比较简单，因此被广泛应用于低气压等离子体诊断中，并迅速成为等离子体诊断技术中强有力的诊断工具之一. 将金属丝伸入等离子体中，施加正向或者负向偏压，便能够收集等离子体中的电子流和离子流，这就是朗缪尔探针的工作原理. 根据得到的探针I-V曲线，可以计算等离子体的电子密度、离子密度、电子能量分布函数(Electron energy distribution function，EEDF)和等离子体悬浮电位等多个参量，其结构及原理如图2所示. 通常来讲，低气压射频等离子体放电处于非平衡状态，EEDF偏离麦克斯韦分布. 通过探针测量电子能量分布，可以深刻地理解等离子体的加热机制和电子的动力学特性，还能计算出某些反应速率[2-3].

Godyak等人在射频等离子体探针诊断方面做出了重要贡献[2-6]，采用高分辨的朗缪尔探针技术系统地研究了单频CCP中EEDF、等离子体密度和电子温度随外界放电参量的变化，发现了CCP中放电模式的转换现象. 韩国KAIST实验室Chang等人采用单探针射频补偿技术，有效地克服了射频干扰，在单频CCP研究方面取得了大量的研究成果[7-10]. 当气压固定在65 mTorr，电流固定为1 A时，实验测量的电子能量概率函数(Electrons energy probability function,EEPF)随放电间隙的变化[9]如图3所示.

(a)电流和电压的定义

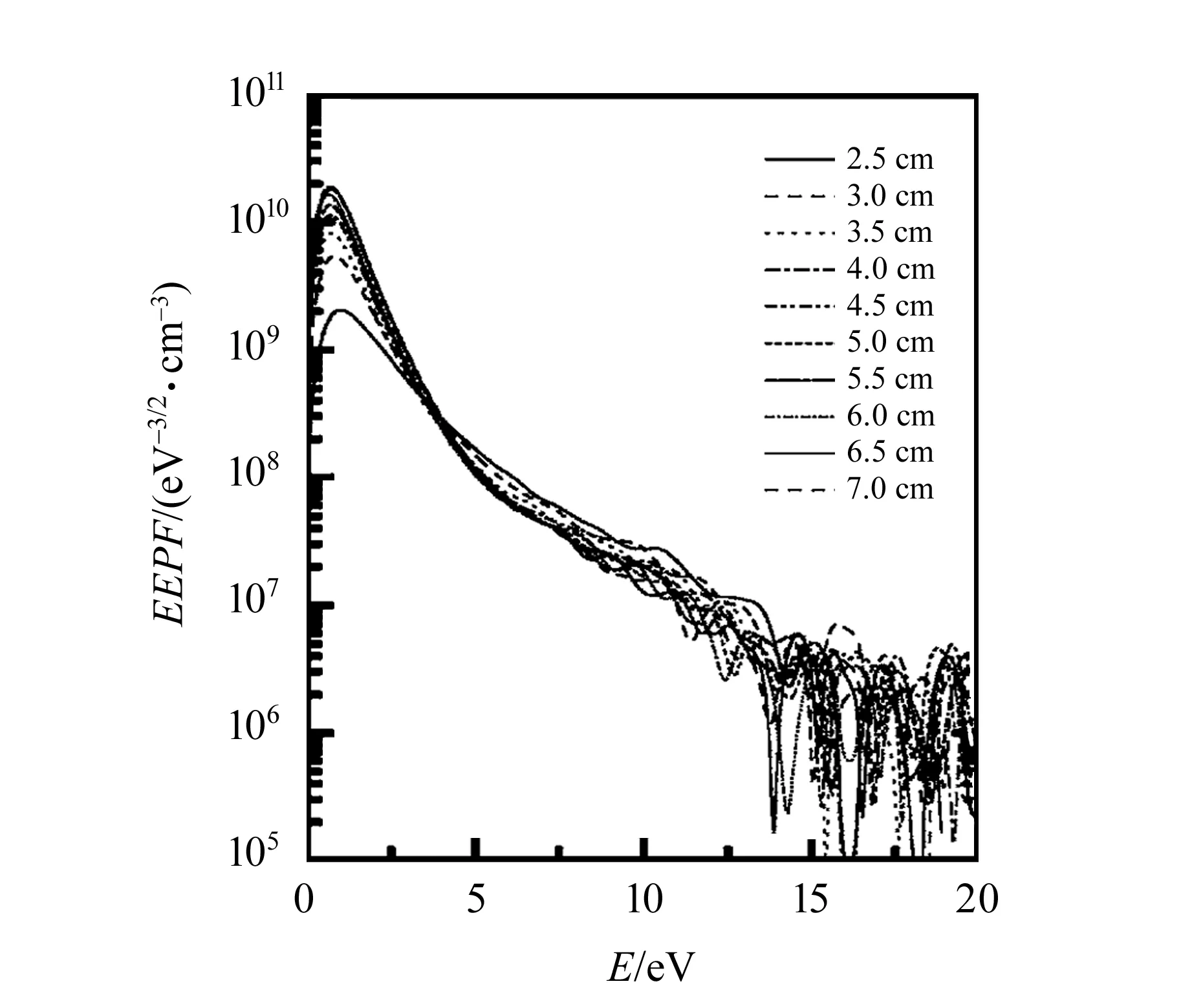
图3 朗缪尔探针测量的不同放电间隙下的EEPF[9]

从图3中可以看出随着放电间隙减小，EEPF的低能电子数量降低，温度升高，而高能电子群的数量和温度基本不变. 对于低能电子密度的降低，文献[9]将其归因于小间隙下等离子体区电场的增强，使得低能电子被加热变成高能电子.

然而，探针诊断也有其难以克服的弱点，即射频干扰. 由双频激励CCP中2个基频振荡产生的高次谐波带来的射频干扰，使射频补偿探针难以工作. 在反应性气体放电中，例如O2或CF4，负离子的存在使得在探针施加正偏压时，除收集电子电流外，还收集到负离子电流，对探针理论提出了挑战. 另外，探针表面会沉积1层C-F绝缘膜，使探针无法有效收集等离子体电流.

2.2 双探针

在大多数情况下，由于CCP空间电位的强烈振荡，朗缪尔单探针测量的I-V曲线受到破坏，很难得到可靠的等离子体参量信息. 双探针(Double probe)把材料、大小和形状完全相同的2个探针插入密度均匀的等离子体中，如果2个探针之间存在电势差，2个探针之间便会有电流流过，示意图如图4(a)所示.

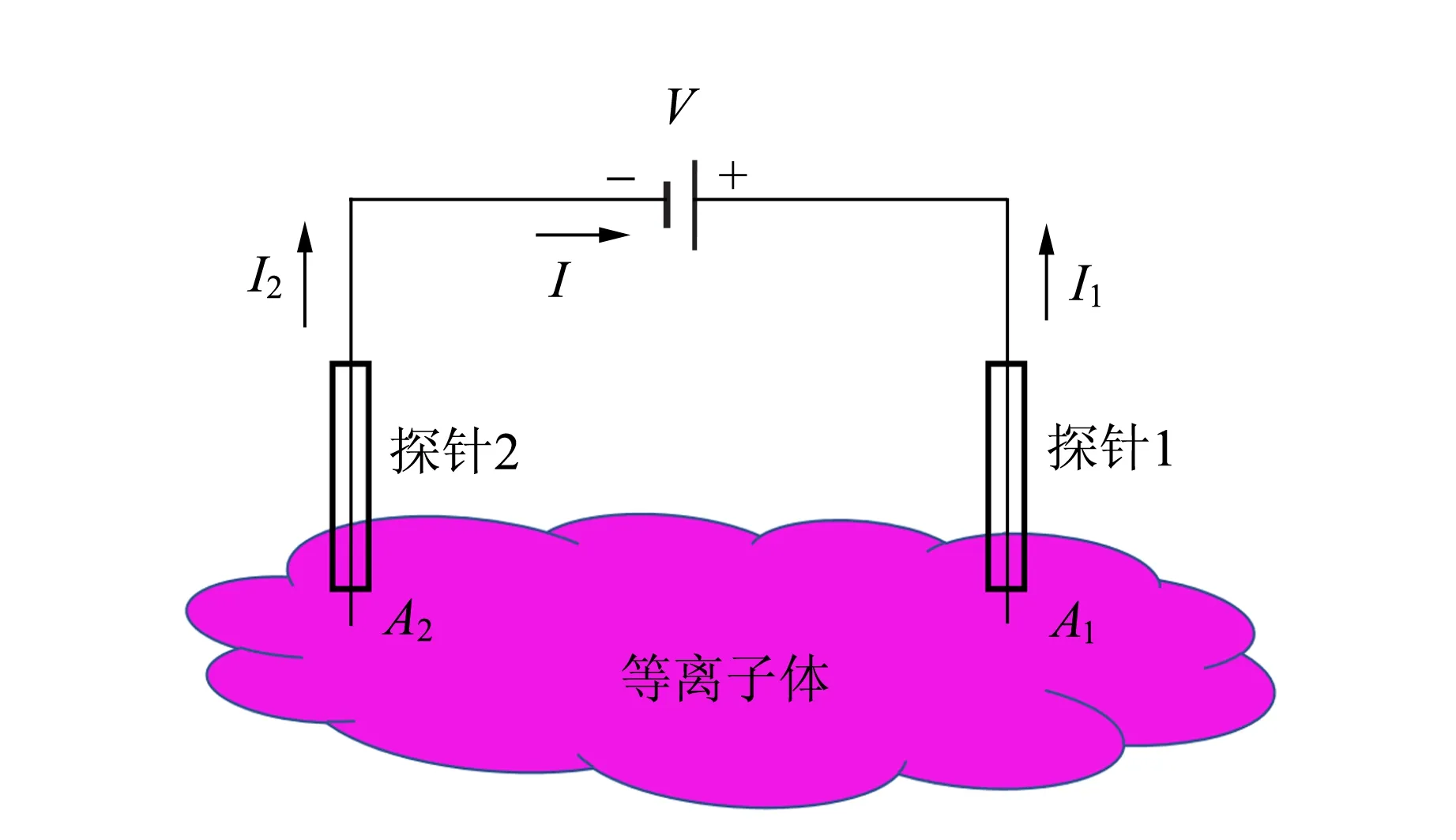
(a)电流和电压的定义

探针尖一般采用钨丝制成，可以很大程度抵抗等离子体的刻蚀. 钨丝的直径一般为0.2 mm，外面套上毛细陶瓷管或石英管，使得2个探针尖(例如5 mm)暴露在等离子体中的长度相等，探针的暴露部分构成收集带电粒子的有效面积，即A=πDL，D为探针尖(钨丝)的直径，L为暴露在等离子体中探针尖的长度.

通过对2个探针之间的电压进行扫描(例如-50～+50 V)，可得到双探针的I-V特性曲线，如图4(b)蓝线所示. 可以看到当扫描电压V的绝对值较大时，离子电流I随着V呈线性增长，这是由于探针周围的鞘层厚度增加，从而导致探针对电荷的有效收集面积A呈线性增加. 因此，需要对探针曲线进行修正，来消除收集面积的增加效应.

I-V曲线修正及电子温度Te和离子密度ni的计算步骤如下：

1)对离子饱和电流区进行线性拟合，拟合直线与纵轴相交的位置即为离子饱和电流Iis.

2)从修正的I-V曲线上减掉线性增长的离子饱和电流，得到修正的I-V曲线，如图4(b)中红线所示.

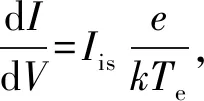
4)基于Iis和Te可以计算出离子密度：

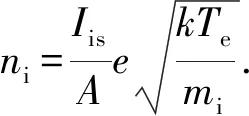
其中，mi为离子质量. 2个探针之间施加的扫描电压无需接地，因此可以将双探针的电路系统悬浮起来，使其不受振荡的等离子体电势的扰动，得到的I-V曲线比较光滑. 双探针的优点是净电流值不会超过饱和离子流，因此能够最大限度地降低对等离子体的干扰. 由于双探针的理论模型是基于麦克斯韦的EEPF假设，因此在测量非麦克斯韦分布的EEPF时，会出现误差. 由于双探针只能收集EEPF中高能尾部的电子，测量的是高能电子群的温度，所以在低气压放电情况下，电子的温度会被高估，从而导致离子密度被低估.

Annaratone等人[11]采用双探针研究了单频CCP放电，发现没有射频补偿的双探针给出了错误的结果，这是由于探针产生了自偏压. Lu等人将双探针进行了“全悬浮”处理，极大地降低了探针电路和地之间的杂散电容，能够有效地屏蔽双频干扰[12]. 该探针系统由双探针、笔记本电脑、数据采集卡和偏压驱动器组成. “全悬浮”是指该系统利用笔记本电池供电，避免射频信号耦合到探针电路中. 采用该探针，Liu等人测量出双频激励下(60 MHz+2 MHz)CCP的等离子体密度[13]. 通过调节平行板之间的距离，Liu等人发现在2 cm间距下，等离子体密度及发光强度出现反常增加，如图5所示. 通过计算机模拟出了该特征，证实了等离子体密度的反常增加是由电子在2个振荡的鞘层之间的反弹共振加热引起的.

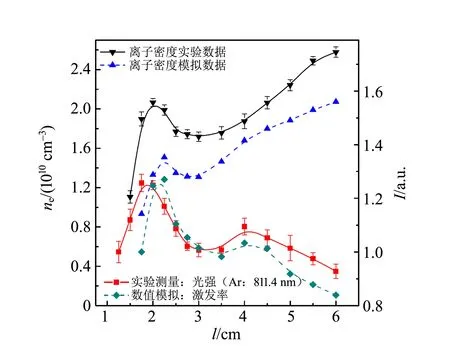
图5 CCP中等离子体密度和发光强度(激发率)随 电极间距的变化[13]

2.3 微波共振探针

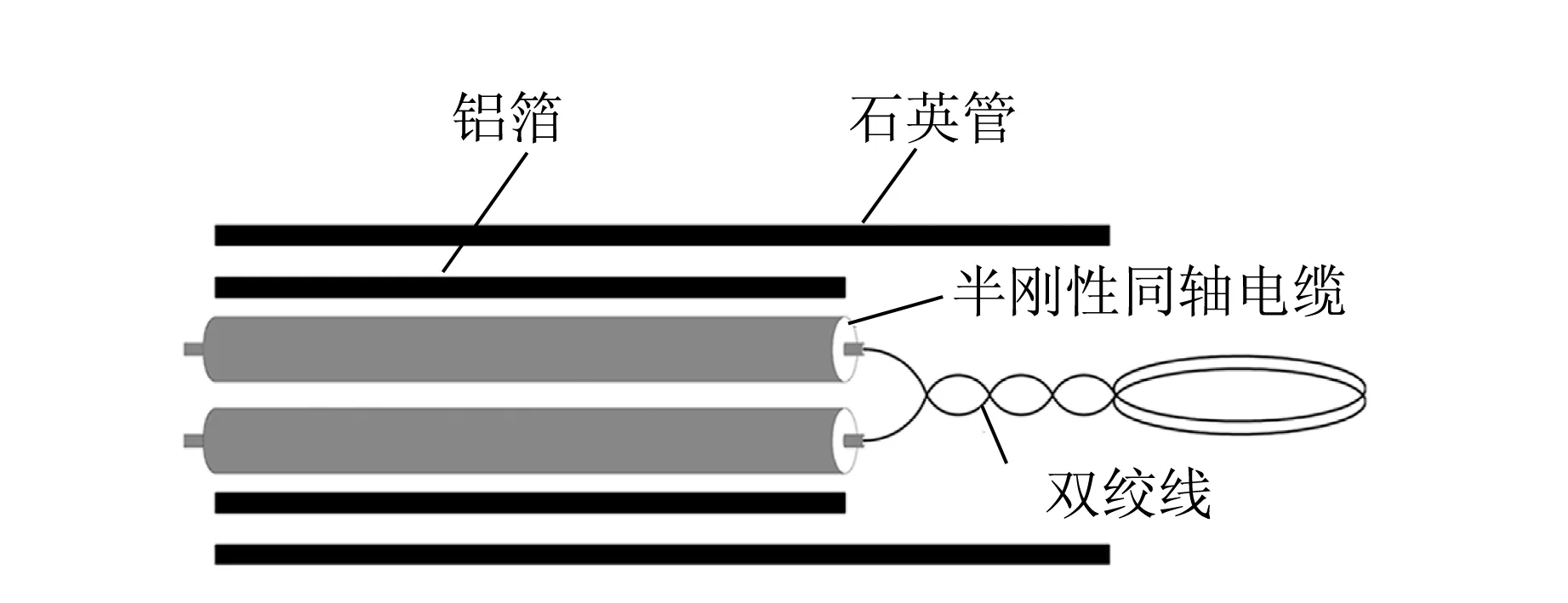
微波共振探针(Microwave resonance probe)是基于微波共振原理对电子密度进行测量的探针，因其外形如“发卡”，所以通常被称为“发卡探针”. 发卡探针最早是由Stenzel[14]在1976年提出来的. Piejak等人将该探针作为基本的等离子体诊断工具应用在CCP的实验研究中，并取得很多研究成果[15-19]. 发卡探针可以用在反应性气体放电环境中，是测量电子密度的有效工具. 发卡探针系统包括U型金属探针头、半钢同轴线、感应线圈、密封介质管等，如图6所示.

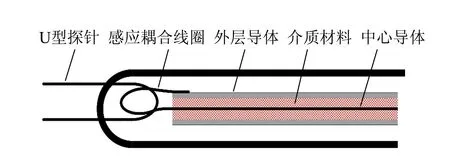
(a)俯视图

将半钢同轴线的一端与微波信号源通过SMA接头连接，将其另一端的外层金属层及介质材料层剥去后，将中心导体弯折，其末端焊接在半钢线的外层导体上，构成了闭合的感应耦合线圈. U型结构与金属感应环互相平行，微波源可以将信号通过闭合线圈耦合到U型结构上.

发卡探针的工作原理可以通过图7所示的等效电路图来说明. 微波源输出的信号可以等效为电压源，在同轴线的感应耦合线圈上会产生电流I1，并在U型结构上感应出电流I2. 对于U型探针，由于两探针之间的距离远小于探针的长度，因此可将其看作是一端短路而另一端开路的传输线. 根据传输线理论，由于负载阻抗为无限大(开路)，传输线中入射的电磁波几乎被完全反射. 当探针长度L与电磁波波长λ满足一定关系时，即L=(2n+1)λ/4，在U型结构上反射波与入射波就会发生相长干涉，形成驻波. 此时右侧的短路端电压必须为0(电压波节)，而电流为最大值(电流波腹)；左侧的开路端电流必须为0(电流波节)，而电压为最大值(电压波腹).

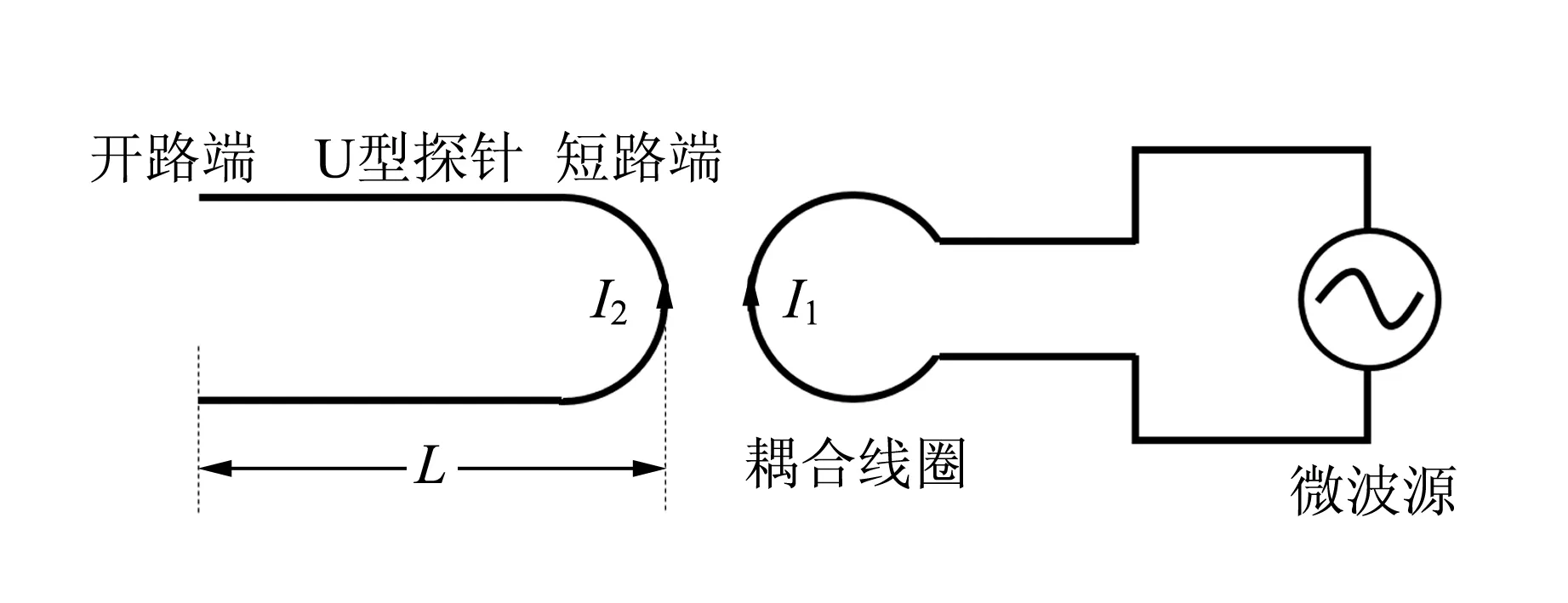
图7 微波共振探针工作的等效电路图

图8给出了发卡探针中前三阶驻波模式下U型结构上的电压和电流分布. 注意这里与图7相反，坐标0点为短路端，L处为开路端. 由于第一阶驻波模式最强，因此取U型谐振单元的第一阶驻波模式，即L=λ/4，来计算真空中的共振频率

(1)

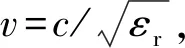
(2)

(3)

(4)

其中，f单位为GHz，ne单位为cm-3.

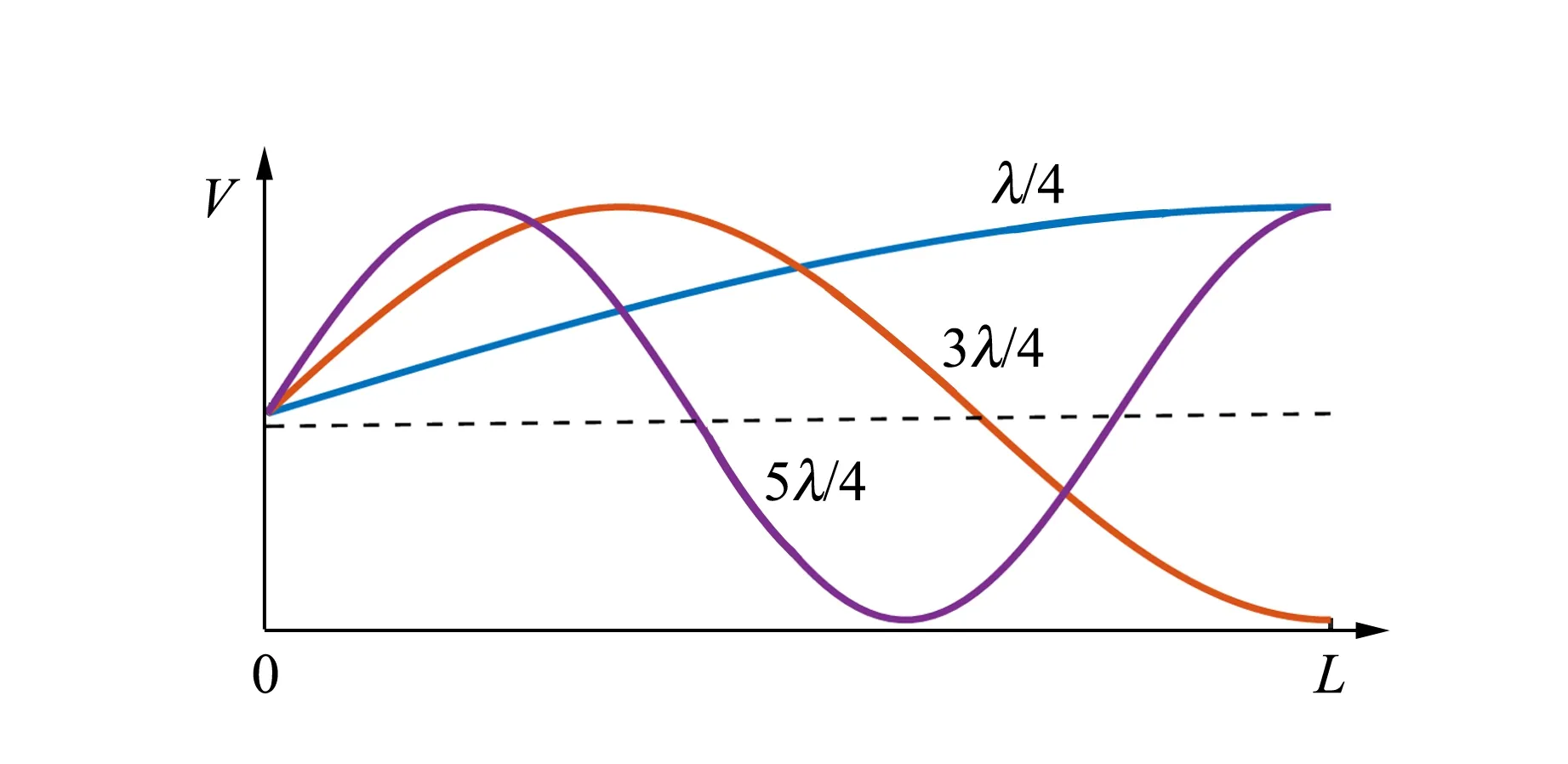
(a)电压分布

若已知发卡探针在真空中的共振频率f0和等离子体中的共振频率fr，通过式(4)就可以计算得到等离子体的电子密度. 通过微波源的扫频模式来驱动U型结构，当扫描频率满足谐振条件，即式(1)或式(2)时，微波在U型结构上发生共振，微波能量被吸收，导致反射能量出现极小值，如图9所示，此时的微波频率为共振频率.

从图9可以看出，起初发卡探针在真空中的共振频率f0低于在等离子体中的共振频率fr. 随着放电功率的增加，fr增加，对应等离子体的电子密度也增加.

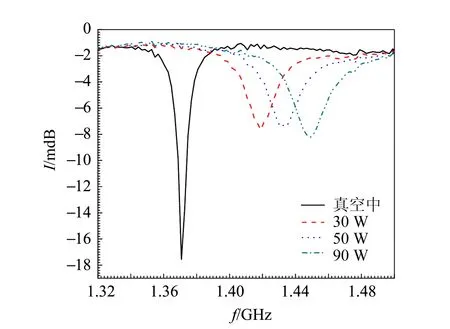
图9 真空中与等离子体中U型结构的反射信号与微波频率的关系[21]

Karkari等人最早将发卡探针应用在双频CCP中[19，21]，在窄间隙双频CCP中测量了电子密度，发现了电子密度强烈的时空振荡. 在Ar/O2/C4F8混合双频容性放电中，随着27 MHz电源的功率增加，电子密度近似线性增加. 在低频(2 MHz)电源功率较高的情况下，电子密度较高. Liu等人采用悬浮发卡探针测量了不同频率CCP的电子密度，发现在氖气放电中，不同驱动频率下的电子密度随着射频电压的增加表现出不同的变化，如图10所示[22].

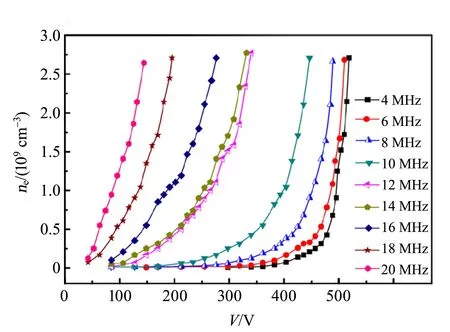
图10 在不同电源频率下CCP氖气放电中电子密度随射频电压的变化[22]

在较高的驱动频率下，电子密度随射频电压呈线性增加，表明放电始终维持在α模式(鞘层加热模式). 在较低的驱动频率下，电子密度在小电压下增加缓慢，在较大电压下增加迅速. 不同的电子密度增长速率表明在低驱动频率下，随着射频电压的增加，等离子体从α放电模式过渡到γ放电模式(电极表面二次电子发射模式).

尽管发卡探针能够测量反应性多组分等离子体中的电子密度，但其本身也存在缺点，例如，该探针只能测量电子密度，而且探针尖比较长(2～4 cm)，其空间分辨测量受到限制. 另外，浸入等离子体的发卡探针周围会形成离子鞘层，共振频率会向真空频率移动，导致电子密度被低估.

2.4 磁探针

磁探针是测量射频等离子体中磁场强度空间分布的重要手段. 根据安培定律，通过磁场的空间分布可以计算出等离子体电流的空间分布，对理解电子加热机制及等离子体中功率沉积至关重要. 磁探针的结构简单，一般由数匝感应线圈制成，其基本原理遵循法拉第电磁感应定律，即当把感应线圈置于交变磁场中时，线圈上的感应电动势Vp(t)等于磁通量Φ(t)对时间的导数

(5)

假设线圈的面积为S，线圈的匝数为N，式(5)可写为

(6)

假设磁场具有简谐振荡形式B(t)=B0sin (ωt)，式(6)变为

Vp(t)=-ωNSB0cos (ωt).

(7)

从式(7)可知在角频率为ω的时变磁场中，线圈上的感应电压振幅正比于磁场的幅值，因此可以通过亥姆霍兹线圈产生的标准磁场来对磁探针的输出电压振幅与磁场振幅进行定标.

虽然磁探针的结构简单，但在实际放电中磁场强度的精确测量却面临诸多挑战. 当探针处在等离子体环境中时，除了磁感应信号，探针线圈还会收集到由振荡的等离子体电势与线圈之间的容性耦合信号(干扰信号)[23]. 因此，提高磁探针的信噪比，即有效地抑制容性耦合(干扰)信号，增强感性耦合(有用)信号成为磁探针设计的关键.

抑制容性信号的方法包括：在探针输出端安装混成连接器[24]，采用中心抽头变压器，等等. 增强感应信号的方法包括：增加磁探针的线圈匝数或线圈横截面，采用有源放大器[25]，采用升压变压器[26]，等等.

Franck等人[27]对比了9种不同类型的磁探针，如图11所示，结果表明采用中心抽头变压器(Center-tapped transformer, CTT)的磁探针具有最佳的容性干扰抑制能力.

(a)平行双线型磁探针 (b)绞单同轴型磁探针 (c)未补偿型磁探针1

Zhao等人[28]设计了新的磁探针电路，包括2个位于可调谐共振电路中的可变电容器以及1个中心抽头变压器，如图12(a)～(b)所示. 采用2种不同的等效电路模型预测了该探针的输出特性，一种为感性信号，另一种为容性信号. 发现通过调节2个可变电容器，可以放大感性信号，抑制容性信号，极大地提高探针输出的信噪比，如图12(c)所示. 红线和蓝线分别代表当感性和容性信号达到最优输出时，2个可变电容器C1和C2的取值组合. 2条曲线的交叉点即为磁探针的最佳运行状态，这时探针的感性信号最大，容性信号最小.

(a)磁探针的结构示意图

Zhao等人[29]采用自主研发的高频磁探针测量出CCP中谐波磁场的空间结构. 同时，将等离子体、电磁传输、等效电路3个模型进行耦合，预测出的平行板间谐波磁场分布与磁探针结果吻合很好，如图13所示. 借助于新型磁探针，该项研究首次在实验上建立了等离子体中高次谐波与均匀性的内在联系，同时从实验与理论角度揭示了造成等离子体不均匀性的物理根源.

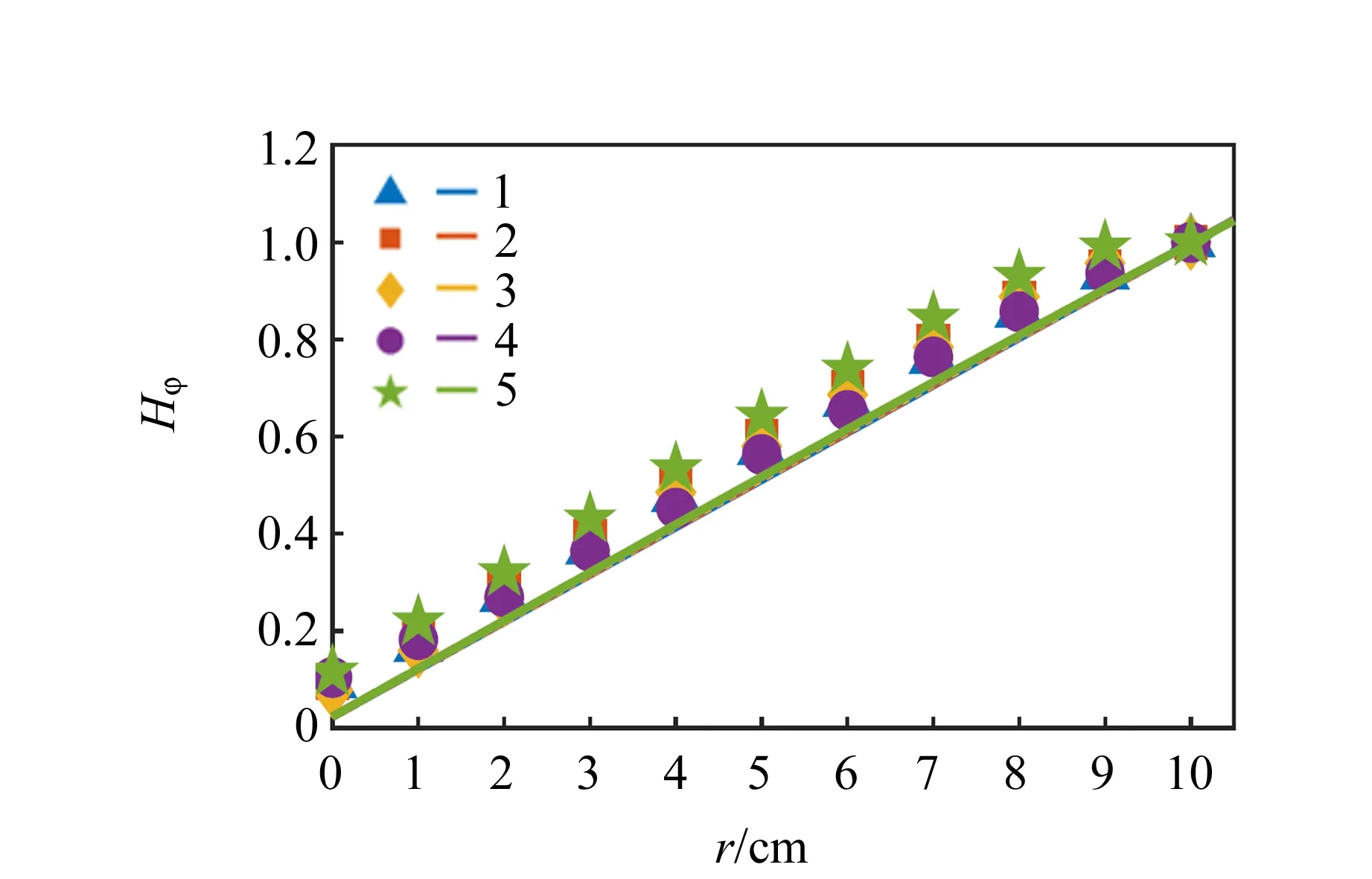
(a)13.56 MHz

3 结束语

等离子体的实验研究在很大程度上依赖于诊断手段的发展. 除了光谱与质谱诊断外，探针诊断是低气压射频等离子体实验研究的重要内容. 本文介绍了几种常见探针的结构、工作原理及典型的测量结果. 这几种探针各具特点，适用于不同的等离子体环境，可以测量不同的等离子体参量，并从不同的角度对等离子体进行实验表征，为研究人员更好地了解射频等离子体的特性提供了条件.