基于自适应位置调节的粒子群MPPT控制方法

游国栋，李兴韫，马 元，徐 滨，侯晓鑫，赵双乐

(天津科技大学电子信息与自动化学院，天津 300222)

太阳能具有安全、环保、资源充足等优点，是一种清洁能源[1].光伏发电是太阳能利用的一种主要形式.随着光伏发电技术的日益成熟，对发电效率的要求也愈发提高，其中，最大功率点是表征发电效率的一个关键指标.然而，在光伏阵列受到不均匀光照时，光伏系统会陷入局部最优状态，严重影响光伏系统对最大功率点追踪(maximum power point tracking，MPPT)的效率，因此，对最大功率点的追踪变得尤为重要.

最大功率点追踪的传统方法包括扰动观测法、电导增量法、模糊控制法等.文献[2]采用直接占空比技术，提出一种变步长扰动观测法，有利于增强光伏系统的稳态性能，但该方法只在传统升压变换器中进行验证；文献[3]使用自适应占空比，提出一种改进的电导增量法，在追踪最大功率点时响应速度快，但运算过程比较复杂；文献[4]结合模糊控制和粒子群算法，提出一种模糊自适应粒子群算法，提高了最大功率点追踪精度；文献[5]通过引入加速度系数，提出一种改进惯性权重的混沌粒子群算法，降低了在最大功率点附近的振荡.

本文提出一种基于自适应位置调节的粒子群MPPT控制方法.首先，运用Tent映射产生混沌序列，对粒子位置进行更新.然后，赋予粒子反捕食的能力，根据捕食者与粒子之间的距离更新粒子位置；通过改变惯性权重取值，控制粒子的飞行速度，进而控制粒子的搜索能力.最后，给速度添加一个极小的增量扰动，避免出现光伏系统陷入局部最优的情况，当每一代的全局最优解相同时，该算法停止，输出结果.通过MATLAB仿真，对该算法进行验证，并与传统粒子群算法结果进行对比.

1 光伏电池模型

1.1 光伏电池模型及特性

光伏电池是太阳光照射半导体P-N结产生光生伏特效应，将光能转化为电能的一种装置.由于单个的光伏电池输出电压比较低，在进行光伏发电时采用光伏阵列的形式，将多个光伏电池通过串并联的形式组成光伏阵列[6].光伏电池的等效电路如图1所示.

图1 光伏电池等效电路 Fig.1 Equivalent circuit of photovoltaic cell

电压电流数学表达模型为

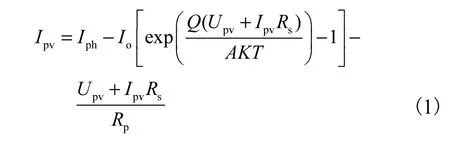
式中：Io为光伏电池内部等效二极管的P-N结反向饱和电流，近似为常数；Iph为光伏电池的光生电流；Ipv、Upv分别为光伏电池的输出电流、输出电压；Rp、Rs分别为并联、串联电阻；Q为电子电荷，Q＝1.6×10-19C；K为玻尔兹曼常数；T为光伏电池所处环境的热力学温度；A为光伏电池内部P-N结的曲线常数.

1.2 不均匀光照情况下光伏电池输出特性

当光伏阵列受到均匀光照时，其输出特性曲线中只有一个峰值点.但是，在实际应用过程中，光伏阵列受外界环境(如温度、辐射照度、云层遮挡等)影响较大，导致光伏阵列的输出特性曲线有多个峰值点；在采用控制方法进行最大功率点追踪时，容易将局部最优误判为全局最优，使系统出现陷入局部最优的情况，降低了发电效率[7-8].光伏阵列在接受均匀光照和不均匀光照情况下的输出特性曲线如图2所示.

图2 光照情况下光伏系统输出特性 Fig.2 Output characteristics of photovoltaic system under illumination

2 粒子群算法及改进算法

2.1 粒子群算法

粒子群算法来自鸟群的启发，将鸟群中的每一只鸟看作是一个“粒子”，鸟群在寻找食物时，相互交流，传递信息[9].在鸟群寻找食物时，会有捕食者进行干扰、捕杀，严重影响粒子群的完整性和寻找食物的范围，因此，粒子群应当有逃避捕食者的能力[10].当有粒子发现食物时，将会传递信息，使附近的其他粒子向食物靠近.从起初无序的寻找到最后有目的的觅食，该过程可以看作是一个寻优的过程.粒子群算法中两个重要的变量是个体最优解(pbest)和全体最优解(gbest).粒子速度vt＋1和位置xt＋1更新如式(2)、式(3)所示.

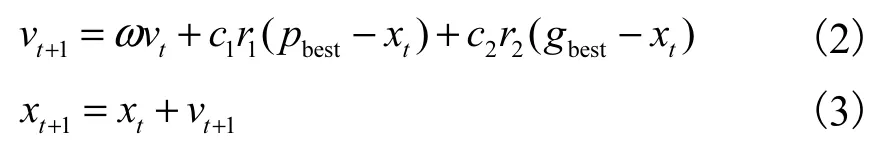
式中：t为粒子更新迭代的次数，vt、vt＋1分别为粒子在t－1代、t代时的速度，xt、xt＋1分别为粒子在t－1代、t代时的位置，ω为惯性权重，c1、c2分别为加速因子，r1、r2分别为[0，1]内的随机数.

2.2 自适应位置调节的粒子群算法

2.2.1 Tent映射

初始化是粒子群算法的第一步，初始化运用得当，可以提高算法的收敛性[11].本文采用Tent映射对粒子群进行初始化，Tent映射表达式为

随机产生[0，1]内的初值记为y0，代入式(4)进行迭代，当达到最大迭代次数时，程序运行停止，产生随机序列.

2.2.2 改进的粒子群算法

为了增强粒子群算法的收敛性能和搜索能力，同时保证粒子的完整性，本文对传统粒子群算法进行改进.设置粒子的搜索空间为D维，共有N个粒子，可将第i(i＝1，2，3，…，N)个粒子在第t代第d(d＝1，2，3，…，D)维表示为此处以2维为例，设捕食者位置为(m1，n1)，粒子位置为(m2，n2)，根据粒子与捕食者的相对距离对粒子位置进行更新，相对距离计算公式为

式中：α为(0，1]中的随机数，Q为一个标准正态分布随机数，M为最大迭代次数，R为报警值.

粒子状态如图3所示.

图3 粒子状态图 Fig.3 Particle state diagram

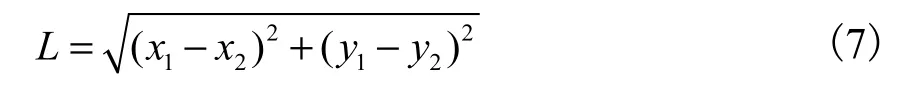
在各个粒子前往聚类中心时，增加惯性权重的取值，提高粒子对局部最优的搜索能力；在各个聚类中心前往全局最优解时，减小惯性权重的取值，提高聚类中心对全局最优解的搜索能力[13].选择适应度最大的聚类中心作为全局最优解，为了避免粒子群出现陷入局部最优的困境，此时给予速度一个小的扰动，观察适应度best( )fg 是否变化，然后多次迭代进行验证.

2.2.3 自适应位置调节的粒子群算法基本流程

(1)设置粒子种群规模N、惯性权重ω、加速因子c1和c2、最大迭代次数M，随机产生一个y0作为第一个粒子，根据式(4)进行迭代，产生N－1个粒子，初始化速度.

(2)根据粒子和捕食者之间的安全距离，更新各个粒子的位置和速度.

(3)评价各个粒子的适应度，将各个粒子的位置和适应度存储在pbest中，将所有pbest中适应度最优的位置和适应度存储在gbest中.

(4)根据适应度，选择聚类中心，将粒子分为若干个粒子群，并更新惯性权重取值.

(5)对于各个聚类中心，与其前一个最优位置相比较，如果较好，则作为当前的最优位置；比较当前所有的pbest和上一次迭代的gbest，更新gbest.

(6)对此时全局最优解施加一个速度扰动，观察适应度f(gbest)是否变化，并进行多次迭代验证.

(7)若达到精度要求或迭代次数，搜索停止，输出结果，否则返回(3).

3 仿真分析

为了验证自适应位置调节的粒子群算法的优化性能，现选取6种具有不同特点的基准函数进行比较测试，结果见表1.对f1、f2、f3、f4均采用30维进行测试，对f5、f6分别采用2维和4维进行测试.参数设置为：粒子种群规模N＝50；惯性权重增加时ω＝0.8，减小时ω＝0.4；加速因子c1＝2、c2＝2，最大迭代次数M＝500，粒子速度范围为[－40，40].粒子群算法(PSO)、麻雀算法(SSA)与自适应位置调节的粒子群算法(APSO)的仿真结果如图4所示.通过对比仿真结果可知，在不同维数、不同测试函数下，本文所提出的方法具有更好的收敛精度且收敛稳定性较好.

图4 3种算法的仿真结果 Fig.4 Simulation results of three algorithms

表1 6种基准函数 Tab.1 Six base functions

以光伏阵列输出电压为参考电压，将所有粒子的位置xi作为光伏阵列输出电压Ui，飞行速度vi作为对参考电压的扰动，粒子群的反捕食能力作为光伏系统的抗干扰能力，对提出的方法在MATLAB软件平台上进行仿真测试，建立的MPPT仿真模型如图5所示[14].仿真模型由光伏阵列、BOOST升压电路、MPPT控制器以及负载模块组成[15].设置温度为25℃，辐射照度为1000W/m2，BOOST拓扑的DC-DC电路的频率为10kHz，MPPT控制器采用基于ATmega16的MPPT控制系统，MPPT控制器控制周期为0.5ms、C1＝470μF、C2＝220μF、L＝2mH.

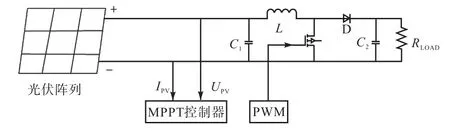
图5 MPPT仿真模型 Fig.5 MPPT simulation model

现将3×3的光伏阵列分别进行不同辐射照度处理，第一列辐射照度为600W/m2，第二列辐射照度为800W/m2，第三列辐射照度为1000W/m2.在传统粒子群算法和自适应位置调节的粒子群算法下，光伏系统输出功率仿真结果如图6所示.

图6 不同算法下光伏系统输出功率图 Fig.6 Output power diagram of photovoltaic system under different algorithms

由图6(a)可知：采用传统粒子群算法在辐射照度为600W/m2时，0.13s后光伏系统进入稳定状态，输出功率为80W；在辐射照度为800W/m2时，0.32s后光伏系统进入稳定状态，输出功率为110W；在辐射照度为1000W/m2时，0.52s后光伏系统进入稳定状态，输出功率为150W.由图6(b)可知：采用自适应位置调节的粒子群算法在辐射照度为600W/m2时，0.08s后光伏系统进入稳定状态，输出功率为100W，与传统粒子群算法相比，输出功率增加20W，效率提高25%；在辐射照度为800W/m2时，0.25s后光伏系统进入稳定状态，输出功率为150W，与传统粒子群算法相比，输出功率增加40W，效率提高36%；在辐射照度为1000W/m2时，0.44s后光伏系统进入稳定状态，输出功率为180W，与传统粒子群算法相比，输出功率增加30W，效率提高20%.

综上所述，当光伏系统输出波形逐渐达到稳定时，采用传统粒子群算法输出波形畸变程度较大，振荡幅度较大；当光伏系统输出波形趋于稳定时，采用自适应位置调节的粒子群算法用时较短，稳态性能更好；光伏系统在不同的辐射照度下，采用自适应位置调节的粒子群算法输出功率均高于传统粒子群算法，在辐射照度发生突变时，光伏系统采用该算法输出功率变化幅度较小.

4 结 论

针对光伏系统多峰值特性，本文提出了一种自适应位置调节的粒子群算法，并通过仿真进行验证.结果表明：运用Tent映射产生粒子群序列，可提高算法的遍历性，降低光伏系统在最大功率点处的振荡；该算法赋予粒子反捕食的能力，可检测出外界环境对光伏系统的干扰，防止输出电压失真；该算法对粒子速度添加一个较小的增量扰动，用于判断粒子群是否获得全局最优解，避免光伏系统陷入局部最优状态.该算法无须选择变量的最优取值，可以更加快速地实时追踪最大功率点，在最大功率点附近振荡较小，提高了光伏系统的发电效率.