UO2芯块运输容器核临界安全分析
庄大杰,孙洪超,孙树堂,陈磊,李国强,张建岗
UO2芯块运输容器核临界安全分析
庄大杰,孙洪超,孙树堂,陈磊,李国强,张建岗
(中国辐射防护研究院,太原 030006)
在开展二氧化铀(UO2)芯块运输容器设计时,应进行临界安全分析,优化容器设计,并通过得出的临界安全指数(CSI)限定可运输货包的数量,确保在任何可信的运输情景下的核临界安全。文中采用蒙特卡罗软件SuperMC对符合要求的国际临界安全手册中6类49个基准实验案例进行建模计算,获得本案例的次临界上限值,再基于运输容器经受正常运输条件与运输事故条件试验的结果,计算得出正常运输条件与运输事故条件下的单货包与货包阵列的最大中子增殖系数eff值。该案例的次临界限值(USL)为0.919 74;UO2芯块运输容器在正常运输条件与运输事故条件下单货包的最大eff值分别为0.286 08,无限阵列货包的最大eff值为0.798 34。UO2芯块运输容器在正常运输条件与运输事故条件下的最大eff值均小于0.919 74,临界安全指数为0,容器设计临界安全性能可确保可运输安全。
运输货包;临界安全;临界安全指数;临界安全计算;次临界限值
临界安全是易裂变材料贮存和运输中所关注的重要问题,国标《放射性物品安全运输规程》及国际原子能机构(IAEA)《放射性物质安全运输条例》中对易裂变货包的临界安全都有明确的规定,要求装载易裂变材料的货包在正常运输条件和运输事故工况下均能保持次临界状态,还要求在多个易裂变货包堆积的阵列条件下仍然能够保证临界安全,即正常运输条件下5个货包、运输事故条件下2个货包均应保证是次临界的[1-2]。《放射性物质安全运输规程咨询材料》中也有关于临界安全评价较详细的介绍,包括临界安全分析模型、分析方法、计算方法和实验验证等[3]。
在进行装载易裂变材料运输容器的设计时,确保运输容器能够经受运输正常条件和运输事故条件下各项实验的考验,保证容器性能满足法规标准中对容器结构、包容、热工、临界和辐射防护等专业的各项要求。在开展UO2芯块运输容器设计时,必须通过临界安全分析,证实单个货包及货包阵列在正常运输条件和运输事故条件下的次临界度,并确定临界安全指数(Criticality Safety Index, CSI),以限定可运输货包的数量,确保在任何可信情景下的核临界安全[4-9]。
文中通过对UO2芯块运输容器进行核临界安全分析,给出蒙特卡罗软件SuperMC对本案例的次临界限值(the Upper Subcritical Limit, USL),以及基于正常运输条件与运输事故条件下的单货包和货包阵列的最大eff值的临界安全指数,建立易裂变材料运输容器的临界安全分析流程,旨在为该类型容器的临界安全的设计关注点提供参考和建议。
1 运输容器及内容物
1.1 UO2芯块运输容器
UO2芯块运输容器外形为长方体箱形,主要由保护外壳、外密封容器、内密封容器、芯块盒等组成。外部尺寸为851 mm×788 mm×775 mm,总质量约396 kg,可以装载11 kg富集度小于90%的UO2芯块,见图1。

图1 UO2芯块运输容器结构
1)保护外壳。保护外壳主要由保护外壳上盖、壳体、石棉橡胶垫、泡桐木减震块等组成。保护外壳上盖法兰为不锈钢板,上盖内部填充100 mm厚的硅酸铝棉毯,防止外部热量通过上盖向内传导,上盖的底部设计有泡桐木。壳体内部填充硅酸铝棉毯,防止外部热量通过壳体向内传导。壳体内侧为泡桐木减震块,侧面竖纹,顶面和底面横纹。
2)外密封容器。外密封容器外形尺寸为418 mm×354 mm×300 mm,采用不锈钢板焊接而成,主要由上盖、下箱体、天然橡胶密封圈、泡桐木减震块等组成。外密封容器是容器的第2层结构,也是容器的第1层防水结构。
3)内密封容器。内密封容器外形尺寸为326 mm× 262 mm×189 mm,采用不锈钢板焊接而成,主要由上壳体、下壳体、天然橡胶密封圈和提手组成。内密 封容器是容器的第3层结构,也是容器的第2层防水结构。
4)芯块盒。芯块盒外形尺寸采用不锈钢板焊接而成。8个芯块盒按照阵列2×2×2的方式分布在内密封容器中。芯块盒之间采用减震材料聚乙烯发泡塑料填充。在芯块盒中,芯块按照2层摆放,每层摆放4列,见图2。芯块盒外包裹用于减震,芯块盒内衬有用于支撑和保护芯块的聚乙烯发泡塑料。

图2 UO2芯块在芯块盒中的示意图
1.2 内容物
UO2芯块运输容器设计装载内容物为235U富集度不超过90%的UO2芯块,属于非特殊形式的一类放射性物品,具体参数见表1。进行临界安全分析时,采用保守参数进行计算。
表1 UO2芯块主要参数

Tab.1 Main parameters of UO2 pellets
注:T.D.为理论密度,为10.96 g/cm3。
2 计算程序及次临界限值的确定
2.1 计算方法及程序
计算采用中国科学院核能安全技术研究所FDS凤麟核能团队自主研发的超级蒙特卡罗核计算仿真软件系统SuperMC完成。SuperMC是一款通用、智能和精准的核设计与辐射安全评价软件。目前可进行中子、光子及耦合输运模拟,可广泛应用于核反应堆设计、辐射物理计算、医学物理模拟、核探测和高能物理仿真研究等领域[10-11]。
2.2 次临界限值的确定
根据国家标准相关规定[12],在没有可直接利用的实验测量数据情况下,可由计算结果解出次临界限值,但所用方法应当与实验数据进行比较,证明是有效的,即满足式(1)要求。

式中:SL为次临界限值,给受控参数系统规定的能使系统在规定条件下肯定处于次临界状态的限制性数值;c为使用特定计算方法对基准实验进行计算得出的eff平均值;Δc为c的偏倚或不确定度;Δm为确保s的次临界性而留出的裕量,Δm取0.05;s为正常条件或可信的异常条件或事故情况下,被评价系统的最大允许有效增殖系数eff的计算值;Δs为计算的统计不确定度,考虑两倍统计偏差。
eff为有效增殖因子,指含有易裂变的有限大系统内,某一时间间隔内产生的中子总数(不包括由中子源产生的中子)与同一时间间隔内因吸收和泄漏而损失的中子总数之比。
Δc是由临界实验偏差、计算方法不确定度以及两者结果差异共同产生的,由式(2)可确定。

式中:Δe为临界实验的不确定度;Δe-c为程序计算结果和临界实验结果的差异;Δmc程序计算的不确定度。
在国际临界安全手册[13-14]中选取了符合要求的6类共49个基准实验案例,部分实验名称见表2。使用SuperMC对49个临界基准试验案例进行建模计算,结合试验数据,可得到即次临界上限值(USL)为0.919 74。
3 临界计算模型及参数
3.1 最大反应性确定
UO2芯块运输容器在经受正常运输条件和事故条件试验验证后,其临界安全性能仍能保证。为确定其各状态下的最大反应性条件,需要结合该容器运输过程中可能的意外事件及依据标准要求开展验证试验的结果,确定临界安全评价对象的各种评价参数。
UO2芯块运输容器在运输过程中需要考虑如下可能影响临界安全性能的意外事件后果:水渗入容器;容器内的木头烧毁;芯块盒可能引起的重新排列;容器之间的间距缩小;容器浸没在水中或埋入雪中。
该容器在依次经受自由下落试验I、自由下落试验Ⅱ、耐热试验以及水泄漏试验后,试验结果如下:芯块盒彼此之间距离变化最大约为8.0 mm;外、内密封容器用的橡胶密封圈完好,石棉垫烧毁,同时缓冲木头顶部局部炭化;经过水泄漏试验后,外、内密封容器未进水。
基于试验结果与要求,确定临界安全评价假定条件:对不影响临界计算的部件进行了简化;被评价单元外部的水反射层为30.0 cm;事故条件下水可以进入保护外壳、外密封容器内部,不进入内密封容器内;考虑芯块盒间距变化,变化范围为−1.2~1.2 cm;事故条件下,缓冲用木头全部被烧毁。
3.2 临界计算模型
UO2芯块运输容器临界计算模型见图3,包括保护外壳、外密封容器、内密封容器、芯块盒等组成。
表2 选取的临界基准试验简介
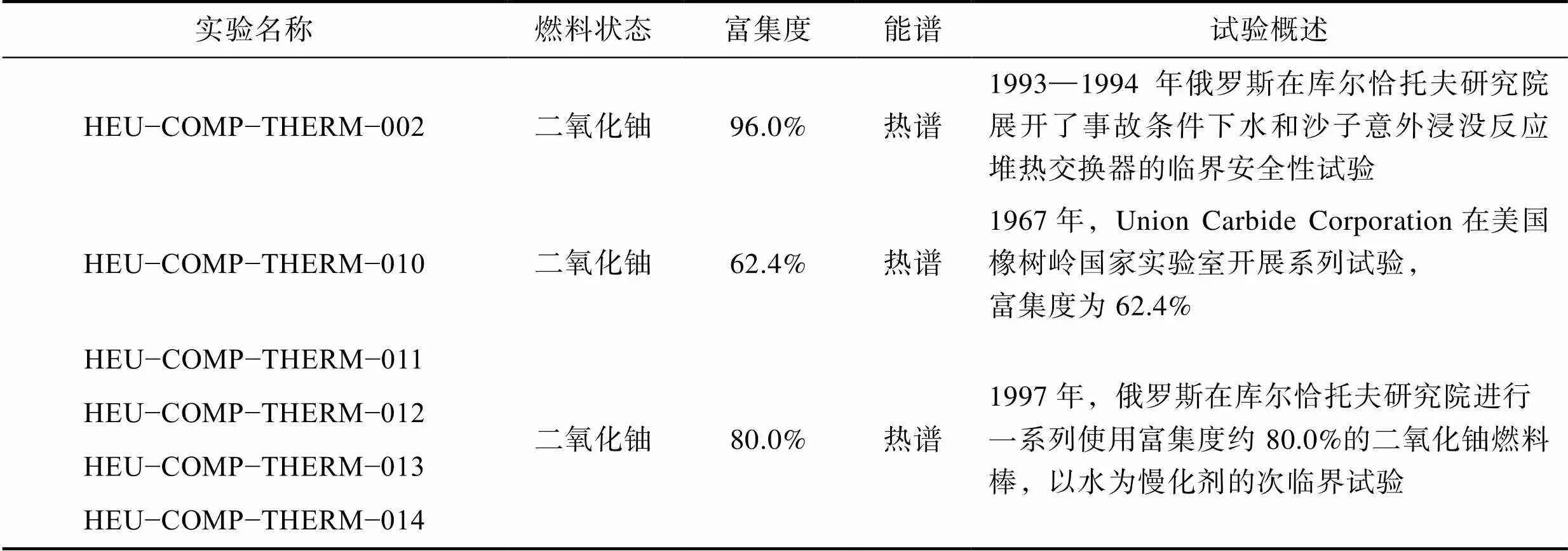
Tab.2 Summary of selected criticality safety benchmark experiments

图3 UO2芯块运输容器的临界计算模型
3.3 材料参数
容器结构材料为S30408不锈钢,隔热材料为硅酸铝棉毯,减震材料为泡桐木、聚乙烯发泡塑料。涉及的材料计算参数见表3。
表3 材料参数

Tab.3 Main parameters of materials
4 临界计算结果及分析
基于临界安全评价假定条件,分别对正常运输工况下和运输事故工况下的单个货包与货包阵列的临界安全进行了建模分析,文中计算方案及各方案最大eff值(含2倍统计偏差)计算结果见表4。
4.1 单个货包评价
以单货包为评价对象,正常运输条件下,eff值为0.22 286。运输事故条件下,方案1–2、1–3计算结果见图4。由图4可知,事故条件下,单个UO2芯块运输货包的eff值随水密度增加而增加,并且水进入的空间越多,密度越大时,eff值越大。在水密度为1.0 g/cm3时,eff值最大为0.286 08。
在基于1–3方案基础上,考虑芯块盒间距变化情况,可知芯块盒间距变化对eff影响不大,见图5。当间距变化量为0时,eff值最大为0.286 08。
由此可见,正常运输条件下,单个货包eff值为0.222 86;运输事故条件下,单个货包最大eff值0.286 08,均小于次临界安全限值0.919 74。
4.2 阵列货包
以阵列货包为评价对象,正常运输条件下,eff值为0.739 46。运输事故条件下,方案2–2、2–3计算结果见图6。由图6可知,事故条件下,阵列货包的eff值随水密度增加而减小,并且水进入的空间越多,密度越小时,eff值越小。在缓冲块木头烧毁,水密度为0时,eff值最大,为0.752 70。
在基于2–3方案基础上,考虑芯块盒间距变化情况,eff值与芯块盒间距变化情况见图7。当间距变化量为0.6 cm时,eff值最大为0.798 34。
表4 UO2芯块运输容器临界安全分析计算方案

Tab.4 The calculaiton case of criticality safety for UO2 pellets transport container

图4 运输事故条件下,单货包keff值随水密度变化的情况

图5 运输事故条件下,单货包keff值随芯块盒间距变化量的情况

图6 运输事故条件下,阵列货包keff值随水密度变化的情况

图7 运输事故条件下,阵列货包keff值随芯块盒间距变化的情况
由此可见,正常运输条件下,阵列货包eff值为0.739 46;运输事故条件下,阵列货包最大eff值0.798 34,均小于次临界安全限值0.919 74。
5 结语
文中采用蒙特卡罗软件SuperMC分析UO2芯块运输容器在正常运输条件与运输事故条件下的临界安全性能。基于芯块的特性及可能的事故景象,选取符合要求的6类49个基准实验案例进行验证,根据基准实验计算结果与试验结果的统计分析,获得使用SuperMC计算该案例的次临界限值为0.919 74。
在进行芯块运输容器临界计算分析时,结合该容器运输过程中可能发生的意外事件以及依据标准要求开展验证试验的结果,确定其各状态下的最大反应性条件以及保守的评价参数。计算结果表明,单货包的最大eff值为0.286 08,无限阵列货包的最大eff值为0.798 34,均小于次临界限值,其临界安全指数为0,在任何可信的运输情景下的其核临界安全性能是可靠的。
[1] GB 11806—2019, 放射性物品安全运输规程[S].
GB 11806—2019, Regulations for the Safe Transport of Radioactive Material[S].
[2] SSR 6—2018, Regulations for the Safe Transport of Radioactive Material[S].
[3] SSG 26—2012, Advisory Material for the IAEA Regulations for the Safe Transport of Radioactive Material[S].
[4] 王学新, 庄大杰, 曹芳芳, 等. AP1000新燃料组件运输货包的临界安全计算[J]. 辐射防护, 2014, 34(2): 97-101.
WANG Xue-xin, ZHUANG Da-jie, CAO Fang-fang, et al. Criticality Safety Analysis to Transport Package of Intact AP1000 Fuel Assembly[J]. Radiation Protection, 2014, 34(2): 97-101.
[5] 李颖虹, 黄灏, 周荣生, 等. 高温气冷堆新燃料元件运输容器临界安全分析[J]. 核动力工程, 2019, 40(6): 64-71.
LI Ying-hong, HUANG Hao, ZHOU Rong-sheng, et al. Criticality Safety Calculation and Analysis of Fresh Fuel Element Transport Containers for High Temperature Gas-Cooled Reactor[J]. Nuclear Power Engineering, 2019, 40(6): 64-71.
[6] 叶佳佳, 陈灵芝. 压水堆乏燃料包装容器临界安全计算[J]. 江西化工, 2019(4): 51-53.
YE Jia-jia, CHEN Ling-zhi. The Criticality Safety Calculation of Spent Fuel Packaging Containers for PWR[J]. Jiangxi Chemical Industry, 2019(4): 51-53.
[7] 张敏, 王婧, 洪哲, 等. CNSC乏燃料组件运输容器临界安全分析[J]. 核技术, 2020, 43(3): 41-46.
ZHANG Min, WANG Jing, HONG Zhe, et al. Criticality Safety Analysis of CNSC Spent Fuel Assembly Transport Container[J]. Nuclear Techniques, 2020, 43(3): 41-46.
[8] 庄大杰, 闫峰, 王学新, 等. 我国在放射性物质运输货包辐射监测中存在的问题[J]. 中国辐射卫生, 2016, 25(4): 480-482.
ZHUANG Da-jie, YAN Feng, WANG Xue-xin, et al. Problems Existing in Radiation Monitoring of Radioactive Material Transport Packages in China[J]. Chinese Journal of Radiological Health, 2016, 25(4): 480-482.
[9] 李航, 周琦, 朱庆福. MOX燃料贮存水池核临界安全分析[J]. 原子能科学技术, 2018, 52(8): 1388-1392.
LI Hang, ZHOU Qi, ZHU Qing-fu. Nuclear Critical Safety Analysis of MOX Fuel Storage Tank[J]. Atomic Energy Science and Technology, 2018, 52(8): 1388-1392.
[10] 曹攀, 周科源, 张强, 等. CEFR–MOX新燃料组件运输货包临界安全计算[J]. 辐射防护, 2019, 39(2): 89-94.
CAO Pan, ZHOU Ke-yuan, ZHANG Qiang, et al. Criticality Safety Analysis on Transport Package of Fresh CEFR-MOX Fuel Assembly[J]. Radiation Protection, 2019, 39(2): 89-94.
[11] WU Y, FDS T. CAD-Based Interface Program for Fusion Neutron Transport Simulation, Fusion Energy Design, 2009, 84: 1987-1992.
[12] WU Y J, SONG H, ZHENG, et al. CAD-Based MonterCarlo Program for Intergrated Simulation of Nuclear System SuperMC, Annals Nuclear Energy, 2015, 82: 161-168.
[13] GB/T 15146.2—2008, 反应堆外易裂变材料的核临界安全, 第2部分: 易裂变材料操作、加工、处理的基本技术准则与次临界限值[S].
GB/T 15146.2—2008, Nuclear Criticality Safety for Fissile Materials Outside Reactors-Part 2: Basic Technical Practices and Subcritical Limits for Handing, Processing and Operations with Fissile Materials[S].
[14] BRIGGS J B. The Activities of the International Handbook of Evaluated Project(ICSBEP)[J]. Journal of Nuclear Science & Technology, 2014, 30(2): 1427-1432.
[15] FF C B L, EJ B B, TMB V M. On a Comparison of a Neutron Monte Carlo Transport Simulation to a Criticality Benchmark Experiment[J]. Progress in Nuclear Energy, 2021, 134: 257-259.
Nuclear Criticality Safety Analysis for the UO2Pellets Transport Container
ZHUANG Da-jie, SUN Hong-chao, SUN Shu-tang, CHEN Lei, LI Guo-qiang, ZHANG Jian-gang
(China Institute for Radiation Protection, Taiyuan 030006, China)
Nuclear criticality safety analysis is an important part of the design safety evaluation of radioactive material transportation containers. During the design of UO2pellets transport container, criticality safety analysis shall be carried out, and the number of transportable packages shall be limited by the calculated criticality safety index (CSI), to ensure nuclear criticality safety under any credible scenario. In this paper, the Monte Carlo software SuperMC is used to verify the 49 benchmark test cases in 6 categories in the international criticality safety manual, and the maximum upper subcritical limit (USL) of this case is 0.919 74. Based on the test results of the transportation container under normal conditions and accident conditions, the maximumeffvalues of single package and package array under normal conditions and accident conditions are calculated. The calculation results show that the maximumeffvalue of single package is 0.28608, and the maximumeffvalue of infinite array package is 0.798 34. The maximumeffvalues of UO2pellets transport container under normal transport conditions and transport accident conditions are both less than 0.919 74. The criticality safety index is 0 for those values are lower than the USL. The container design critical safety performance can ensure the critical safety during transportation.
transportable package; criticality safety index; criticality safety analysis; the maximum upper subcritical limit
TB485.3;TL731
A
1001-3563(2022)11-0168-06
10.19554/j.cnki.1001-3563.2022.11.022
2021–11–14
庄大杰(1984—),男,硕士,副研究员,主要研究方向为放射性物品运输安全。
责任编辑:曾钰婵

