财政激励政策、人才配置与经济增长——基于微观视角的研究

张伟亮 宋丽颖

内容提要：本文在罗默模型的基础上进行拓展，引入政府部门，从微观视角研究财政激励政策对人才配置与经济增长的影响。主要研究结论为：（1）对中间产品生产部门减税和补贴可以促进从事研发的人才数量上升，起到引导人才进入研发领域的作用，激励新知识生产，从而促进经济的内生增长。但是，减税表现出边际效应递减，而补贴则呈线性效应。（2）减税与补贴效应相等时，减税强度与补贴强度的倒数满足线性关系。（3）从社会效率来看，减税与补贴可以缓解无政府部门时均衡研发人才数量的无效率，提高经济福利水平，促进经济长期增长。此外，经济中存在一个家庭效用最大化时的研发人才数量，即研发人才数量黄金水平。本文研究为政府采用财政激励政策改善人才配置、激励创新活动、促进经济增长提供了理论基础。

随着全球经济进入“后疫情时代”，各国经济下行压力凸显，创新越来越成为经济持续增长的核心动能。人力资本投入是创新水平持续提高的主要动力。在现阶段，我国创新与人力资本积累呈现出显著的不平衡，突出表现之一是创新增速显著低于人力资本积累增速。从数量来看，随着我国高等教育体系的完善，人才不断被培养，在某些领域甚至出现了“拥挤”的现象。但是，创新水平并未同比例上升，二者之间的缺口呈逐年增长的趋势（谭莹和李昕，2019）。这反映出我国人力资本创新转化率不足，而人才配置的不平衡是其中的主要矛盾（赖德胜，2011）。因此，要实现我国创新驱动发展的战略目标，关键是从前期扩大人才规模的外延型模式逐步转化为关注于人才配置效率、充分发挥人才潜能的内涵式模式，提升创新水平，加快实现“创新发展战略目标”。

在经济增长的压力下，部分省市出台一系列财政激励政策，通过税收优惠、补贴等方式吸引创新型企业和人才，旨在促进创新能力的提升。在充分竞争的劳动力市场上，人才不仅可以从事创新活动，也可以从事生产性活动。那么，基于理性人假设的个体决策下，这些财政资源倾斜能否达到政府预期目标呢？本文通过构建模型，试图从微观视角回答减税与补贴对人才配置、经济增长和经济效率的影响。此外，是否存在一个社会最优的激励水平也是本文的研究内容。

一、文献综述

新经济增长理论强调人力资本对创新的促进作用，认为创新是经济增长的源泉。发展经济学理论认为，创新是一种市场行为，在企业家追逐利润最大化的过程中会推动创新，从而推动经济增长。但是，这无法很好地解释人力资本存量与创新水平的跨国差异，其原因可能就是忽略了人才配置问题（庄子银，2007）。

国外关于人才配置的研究起步较早，研究内容主要集中在人才配置与创新活动和经济增长上。Baumol（1990）认为人才配置影响创新绩效，人力资本在生产性活动和非生产性活动之间的配置深刻影响技术创新。Murphy et al.（1991）通过归纳发现，工程师占比较高的国家通常经济增长较快。这是因为人才资源如果进入生产部门的话，则人力资本可以提高生产效率，促进创新活动，从而促进经济增长。如果人才成为寻租者，寻租只是财富的再分配，则无益于经济增长。此后，关于寻租、腐败与经济增长的文献大量出现（Murphy et al.，1993；Acemoglu，1995），但是直接讨论人才配置对经济增长的研究较少。Hsieh et al.（2013）利用Roy 模型分析了1960-2010 年美国人才配置对经济增长的影响，估算出美国大约15%-20%的人均产出得益于人才配置的改善。Ebeke et al.（2015）从寻租的角度分析了发展中国家人才错配现象，通过使用69 个发展中国家数据发现，人才配置的关键因素是制度。当制度质量差时，人才更倾向于进入垄断部门进行寻租，造成人才错配，抑制经济增长。此外，Zhang et al.（2010）、Arcand et al.（2015）等学者研究了部门间人才配置对经济的影响。

相较于国外，国内对人才配置的研究不多，且研究多集中在宏观数据检验上。李晓敏和卢现祥（2010）通过构建人才配置模型，从理论上分析了企业家配置占比对经济增长影响，发现随着企业家占比的上升，经济增长率上升。李世刚和尹恒（2014，2017）在外生化科研机构创新的前提下研究了人才在企业与政府间的配置问题，发现寻租导致的人才错配会产生显著的社会成本，且人才在企业与政府间存在一个最佳分配比例，若偏离该比例，则会损害经济增长。赖德胜和纪雯雯（2015）通过建立模型，提出公共部门人力资本积累对创新活动具有抑制作用，并运用1997-2012 年省级面板数据模型进行实证检验，发现人力资本集中在垄断部门与政府是制约我国人力资本有效使用的原因。葛立宇（2018）使用2009-2014 年省级面板数据实证检验了要素市场扭曲、人才配置与创新强度。研究发现社会人才的错配显著抑制了地区创新强度。王启超等（2020）研究了中国人才配置“脱实向虚”倾向，有限的人才资源过度配置到金融业显著降低了中国实体经济全要素生产率。此外，还有一部分研究集中在我国人才配置情况的描述上（赫鹏飞和宇小兵，2016；刘兵等，2017）。

综上所述，国内外学者从不同角度的研究得出了人才配置对经济增长有显著影响的结论。本文研究意义在于：基于前人的研究，在模型中引入政府部门，将财政激励政策与人才配置关联起来，从而探讨财政激励政策对人才配置和经济增长的影响，以及减税与补贴之间的区别与联系，并进一步分析达到社会效率时的政策均衡解。本文研究结果为各级地方政府正确发挥市场机制、制定财政激励政策有效配置人才资源以促进经济增长提供了理论依据。

二、理论分析

基于本文的研究主题——财政激励政策、人才配置与经济增长，在罗默模型的基础上进行拓展。首先需要指出的是，本文研究核心为政府通过财政激励政策影响人才配置，进而促进经济增长，所指的人才配置为市场经济部门之间的人才分布，不考虑人才流入政府和部分垄断行业的情况。一方面，与总就业人数相比，每年政府和垄断行业吸纳的人员数量很有限；另一方面，企业是创新主体①习近平总书记在科学家座谈会上强调，“要发挥企业技术创新主体作用，推动创新要素向企业集聚，促进产学研深度融合。”，这样处理有利于聚焦本文的研究对象。

定义人才为拥有某种专门技能的人群，人才配置为人才在研发活动与生产中间产品活动中的分布。假设经济中有四个部门：中间产品生产部门、最终产品生产部门、家庭与政府。其中，中间产品生产部门进行研发活动，提出新知识，并将新知识转化为包含新知识的中间产品，且具有垄断势力，可以获取超额利润。最终产品生产部门利用中间产品生产最终产品，处于完全竞争市场，均衡时利润为零。人才位于家庭部门，为研发与中间产品生产提供劳动，收取工资。政府负责财政政策的制定，通过税收、补贴等形式影响经济。

（一）基准模型

首先考虑不包含政府部门的情形，以此作为基准模型。

1.最终产品生产部门

假设新知识均匀分布在［0，A］区间上，A 代表经济中的新知识总量，生产中间产品时劳动可以一对一转化。经济中所有的生产要素均为包含新知识的中间产品，最终产品生产函数为伊瑟生产函数：

式（1）中，生产最终产品的中间产品数量为Li，φ 为弹性系数。令人才总数为常数为从事研发的人才数量，LY为从事中间产品生产的人才数量，则有假设生产每一种中间产品的工人数量是相同的，有Li=LY/A，则式（1）可写为②伊瑟生产函数可以如此变形的原因是已经假设了生产中间产品时劳动可以一对一转化。：

记pi为中间产品i 的价格，考虑最终产品厂商单位产出的成本最小化问题，构建拉格朗日函数，如式（3）所示：

最终产品厂商的选择变量为Li，其一阶条件为：

由此可得中间产品的需求曲线，如式（5）所示：

从式（5）可知，中间产品的需求曲线向下倾斜，需求弹性η=1/（1-φ）。

2.中间产品生产部门

新知识的生产函数如式（6）所示：

其中，B 为常数，表示研发实力，并假设A0＞0。式（6）同时也表明了已有的知识对新知识生产的作用。

假设人才可以在最终产品生产部门与中间产品生产部门之间自由流动，则根据式（6），任何部门都可以按Wt的工资水平雇佣1/BAt单位的劳动用于生产一单位新知识。人才自由流动的假设要求出售包含某种知识的中间产品的利润现值等于成本，记π 为获得的利润，如式（7）所示：

3.家庭部门

假设家庭无限期存活，目标是效用最大化，效用函数采用相对风险规避系数不变的形式，目标函数如式（8）所示①这里实际上是把家庭成员数量标准化为1，这样避免了对于家庭数量的讨论。实际上，如果不做此处理，也可以得到相同的结论。：

其中，Ct为家庭在第t 期的消费数量，ρ 为时间偏好率。

相应地，家庭部门的预算约束为：

式（9）中，r 为利率，X0为初始财富水平，Wt为收到的工资水平。

4.其他假设

假设劳动力市场完全竞争，则中间产品生产部门与最终产品生产部门支付的工资水平是相同的。经济中产出的唯一用途为消费，即此外，由于所有的经济个体是相同的，因此会选择相同的消费路径。

（二）模型均衡值求解

在经济均衡时，人才流动停止，即LAt=LA，LYt=LY。此时，从式（6）可知，新知识增长率gA=BLA，为一个常数。根据式（2），Y 的均衡增长率，即均衡经济增长率 gY=（1-φ）/φ×gA=［（1-φ）/φ］BLA。由于经济中产出的唯一用途为消费，故消费的均衡增长率gC=gY。此外，由于中间产品价格加成不变，结合规模报酬不变和竞争性市场的假设，可知工资的均衡增长率gW=gY。

经济中的利率水平r 由家庭的最优选择决定。为计算方便，定义有效人均消费为ct，有效人均工资为 wt，则有 Ct=Atct，Wt=Atwt。依据式（8）、式（9）构建拉格朗日函数，如式（10）所示：

求解可得式（11）：

其中，gAt为新知识增长率。由于 Ct=Atct，故有求解可得经济中的利率水平，如式（12）所示：

根据微观经济学的标准结论，在生产者具有垄断势力时，制定的利润最大化价格为η/（η-1）×MC。其中，η 为需求弹性。对中间产品生产部门而言，需求弹性η=1/（1-φ）边际成本为Wt，故对中间产品生产部门收取的价格为Wt/φ。因此，任意时点的利润为：

利润的均衡增长率 gπ=gW-gA=［（1-2φ）/φ］BLA。则任意时点利润现值如式（14）所示：

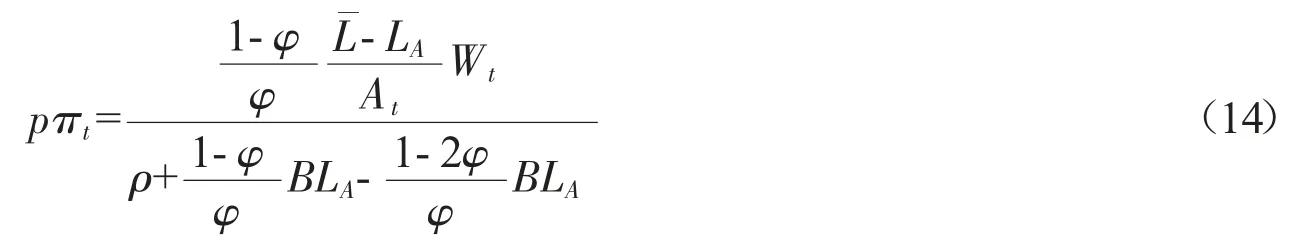
根据式（7），均衡时，有：

解得①由于人数不可能为负，故作此处理。：

此即为经济均衡时从事研发的人才数量。同时，均衡的经济增长率为：

（三）引入政府部门

政府部门可以通过不同的财政激励政策影响人才配置，主要考虑减税与补贴两种政策，探究其对LA的影响。

1.对中间产品生产部门价格进行减税

假设减税强度（即中间产品价格的减税比例）为tax＞0，则中间产品生产部门得到的价格变为（1+tax）Wt/φ，任意时点的利润为：

同样地，减税后任意时点利润现值如式（19）所示：

令其等于Wt/BAt，求解均衡时的LA，即有：

仅考虑LA＞0 时，将其对tax 求一阶与二阶导数，可得：

可以看到，随着减税强度的上升，从事研发的人才数量LA上升，表明减税可以起到引导人才进入研发领域的作用，促进新知识的产生。但是，这种促进作用随着减税强度的上升而下降，表现出边际效应递减。此外，影响从事研发的人才数量的参数主要为最终产品生产要素弹性系数φ、家庭时间偏好率ρ、研发实力B 与人才总数。

在确定均衡LA后，即可得新知识增长率、均衡经济增长率、均衡消费增长率以及均衡工资增长率，即：

可以看到，得益于减税对从事研发人才数量的促进效应，减税进一步会促进新知识增长率、均衡经济增长率、均衡消费增长率以及均衡工资增长率的上升，这实际上是促进了经济的内生增长，但这种促进作用也存在边际效应递减。需要特别注意的是，家庭时间偏好率的上升会降低减税对经济内生增长的促进作用。这是因为时间偏好率越大，均衡的研发人才数量越低，相应地经济增长率越低。这与现实状况相一致，即当家庭时间偏好率上升时，人们更倾向于当前消费，快速将才能变现，导致研发人才流失，不利于经济长期增长。

2.对中间产品生产部门进行补贴

假设对中间产品生产部门进行每期为Gt=kWt/At的补贴①从本质上来说，假设补贴与单位有效劳动工资率成正比。这是基于补贴的动机，即在知识较少时，生产新知识需要更多的补贴。但是当经济中的研发创新达到一定规模后，补贴就可以逐渐减少。另外，根据前面的假设，进行研发的唯一成本为工资，随着工资水平的上升，补贴也需要相应上升，才可以有效激励新知识生产。此外，如此假设有利于模型得到解析解，更易分析。，定义k＞0 为补贴强度，则任意时点的利润为：

遵循相同的逻辑，可求得均衡时的LA，即有：

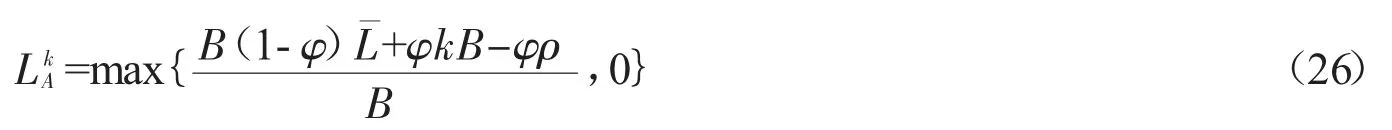
仅考虑LA＞0 时（下同），将其对k 求一阶与二阶导数，可得：

可以看到，随着补贴强度的上升，从事研发的人才数量LA上升，表明补贴可以起到引导人才进入研发领域的作用，促进新知识的产生。但是，根据假设，0＜φ＜1，补贴强度一单位的上升只能带来LA不足一单位的上升。与减税不同的是，补贴对LA的促进作用是线性的，并未表现出边际效应递减。影响从事研发的人才数量的参数同样为最终产品生产要素弹性系数φ、家庭时间偏好率ρ、研发实力 B 与人才总数。

与减税类似，此时可以计算新知识增长率、均衡经济增长率、均衡消费增长率以及均衡工资增长率，如式（29）（30）所示：

同样也可以看到，新知识增长率、均衡经济增长率、均衡消费增长率以及均衡工资增长率均高于没有补贴时的情况，即补贴促进了经济的内生增长。同时，家庭时间偏好率的上升降低了补贴对内生增长的促进作用。

3.减税与补贴效应相等时的情况

由上面的分析可知，减税与补贴对经济造成的影响是不同的。为得到效应相同时减税强度与补贴强度的关系，联立式（20）（26），可得：

图1 减税强度、补贴强度与均衡研发人才数量

（四）财政激励政策对社会效率的影响

在前面分析的基础上，可以进一步分析财政激励政策对社会效率的影响。由于经济并非完全竞争，因此由各部门自主决策带来的分散均衡不会是社会效率，定义社会效率为代表性家庭效用最大化。

作为对比，计算没有政府部门下代表性家庭效用最大化时研发人才数量LA。根据式（2），代表性家庭在t=0 时的消费为：

根据产出与消费的增长率，并结合式（8），可得代表性家庭效用，如式（33）所示：

求解式（33），并对LA求导，即可得代表性家庭效用最大化时研发人才数量LA，即：

因此，如果希望通过减税或补贴使经济达到社会效率，那么减税强度或补贴强度必须满足式（35）（36）所规定的条件，可以看到其与、φ、ρ 与 B 相关。在 tax＜taxgold或 k＜kgold时，提高减税或补贴强度有利于改善社会效率，且有利于经济的长期增长与福利水平的提升。在tax＞taxgold或k＞kgold时，提高减税或补贴强度会使均衡研发人才数量进一步偏离黄金水平，降低社会效率与福利水平，此时应当削减减税或补贴强度。

（五）给予家庭财政激励政策的讨论

在前面的分析中，减税与补贴都是针对企业的。然而，这些政策也可以针对家庭，例如，政府意图通过减税与补贴吸引人才进行研发活动，从而促进创新。但是，在本文的模型中，劳动力市场是完全竞争的，唯一有垄断势力的是生产新知识、并将其转化为中间产品的中间产品生产部门。因此，家庭由于财政激励政策所获得的超额收益将会通过市场机制转移至中间产品生产部门，这种情形与现实经济中劳动力市场高度竞争、人才“内卷”的现象相吻合。在这种情况下，针对家庭的财政激励政策就等价于直接给予企业减税或补贴。

三、研究结论与政策启示

本文在罗默模型的基础上进行拓展，引入政府部门，从微观视角研究财政激励政策对人才配置与经济增长的影响。主要研究结论为：

第一，对中间产品生产部门减税和补贴可以促进从事研发的人才数量上升，起到引导人才进入研发领域的作用，激励新知识生产，从而促进经济的内生增长。但是，减税的这种促进作用随着减税强度的上升而下降，表现出边际效应递减；补贴的这种促进作用是线性的。影响政策效果的其他因素主要为最终产品生产要素弹性系数、家庭时间偏好率、研发实力与人才总数。

第二，减税与补贴效应相等时，减税强度与补贴强度的倒数满足线性关系。当减税强度与补贴强度小于二者效应相等的情况时，有减税下的均衡研发人才数量大于补贴下的均衡研发人才数量，反之则反是。这表明在不同的减税强度与补贴强度下，其政策效果存在显著差异。

第三，从社会效率来看，在没有政府部门的情况下，经济的分散均衡是无效率的，均衡研发人才数量无法达到家庭效用最大化的社会效率水平，而减税与补贴可以缓解这种社会无效率。但是，研发人才数量并非越多越好，经济中存在一个家庭效用最大化时的研发人才数量，即研发人才数量黄金水平。该黄金水平大于经济分散均衡下的均衡研发人才数量，若希望通过减税或补贴使经济达到社会效率，那么减税强度或补贴强度必须满足一定条件，此时经济为最优增长，否则不利于社会效率的改善与福利水平的提升。

本文研究的发现具有显著的政策含义，其中最重要的政策启示是：财政激励政策可以有效促进研发人才数量上升。在我国经济迈向高质量发展的阶段，改善人才配置有助于激励创新和促进经济增长，财政激励政策大有可为。然而，在制定具体政策过程中，要关注到不同政策之间的差别，并且明确其他参数对政策效果的影响。需要注意的是，家庭时间偏好率的上升会削弱财政激励政策的效应，政府需要在制定政策过程中注重将短期利益与长期利益相结合，营造积极创新、追求长远利益的社会氛围，缓解社会浮躁，引导人才积极进入研发领域。此外，需要注重财政激励政策对社会效率的影响。由于研发人才数量黄金水平的存在，制定相关政策过程中需要审慎评估，促进社会效率的改善、人民福利水平的提升和经济的高质量发展。

最后需要说明的是，本文用一个较为简单的框架来刻画经济社会运行，未考虑人才流入公共部门（包括政府机关、自然垄断或行政垄断部门）等情况。然而，经济下行压力加大的时代背景下，越来越多的人才谋求进入这些部门，人力资本未充分转化为创新活动。这可能是人才配置失衡的另一个重要原因，也是本主题研究进一步拓展的方向。