一种异型沉箱浮游稳定性高效计算方法

马 勇，方 波，谭彬政

（中交第四航务工程勘察设计院有限公司，广东广州 510290）

引言

国外某港口升级扩建项目，工程内容为新建一座15 万t 级的现代化集装箱码头和一座5 万t 级的滚装码头，码头结构采用传统的重力式沉箱方案，标准沉箱为规则的矩形截面，但因在集装箱码头与滚装码头交接处，码头岸线存在约124°的夹角，为保证码头岸线的平顺衔接，需在岸线相接位置设置一组横截面不对称的异型沉箱，其结构尺寸如图1所示。

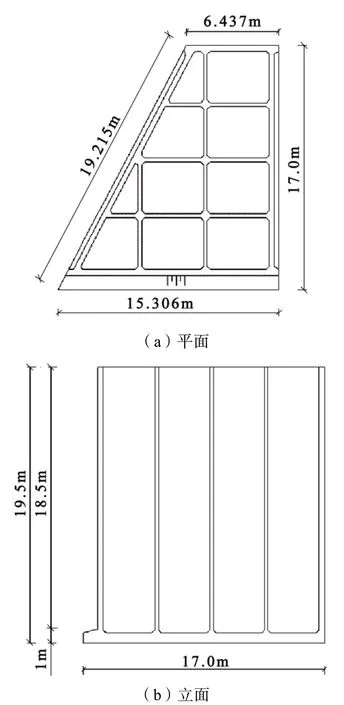
图1 异型沉箱示意

对于横截面不对称的异型沉箱，若采用传统的方法计算其浮游稳定性，计算过程繁琐，且很难求解准确的计算结果[1]。为了解决这一难题，通过分析研究，提出了一套基于AutoCAD 和Excel 的高效求解方法，主要求解步骤如下：

1）基于材料力学的转轴公式和惯性矩圆理论联立求解得到不对称截面的最小惯性矩及相应的形心轴；

2）利用AutoCAD 建模准确计算沉箱的几何属性；

3）根据沉箱浮游稳定的计算原理，结合已求得的沉箱几何属性，联立相关数据的约束方程；

4）利用Excel 规划求解功能求解上述约束方程；

5）求得各箱格内所需加注压载水高度，即求解完成。

通过工程实践验证，该方法的理论计算结果与工程实际结果基本一致，有效解决了异型沉箱浮游稳定性计算的难题。

1 沉箱浮游稳定性的计算原理

在沉箱下潜、拖运、安装过程中，为保证作业安全，需对沉箱的浮游稳定性进行验算，并应满足以下两个条件[2-3]：

条件一：沉箱自身呈水平状态，即沉箱顶面与水平面之间的夹角为0°，这要求沉箱的重心和浮心必须在同一条垂线上，重力和浮力对沉箱水平截面中的任一轴取矩均相等，满足以下公式：

式中：

G为沉箱和压载物的总自重（kN）；

a为重心到计算轴的水平距离（m）；

F为沉箱所受浮力（kN）；

b为浮心到计算轴的水平距离（m）。

通常情况下，沉箱在没有压载的情况，难以满足上述条件，需通过压载物将沉箱调平。

条件二：按照规范要求确定合适的沉箱定倾高度[4]：

1）对于短距离浮运工况（同一港区或30 n mile以内的运程），m≥0.2 m;

2）对于远距离浮运工况（夜间航行或30 n mile以上的运程），固体物压载，m≥0.3 m；液体压载，m≥0.4 m。

定倾高度的计算公式如下[4]：

式中：

m为沉箱定倾高度（m）；

ρ为沉箱定倾半径（m）；

a为沉箱重心到浮心的距离（m）。

沉箱定倾半径按照如下公式计算[4]：

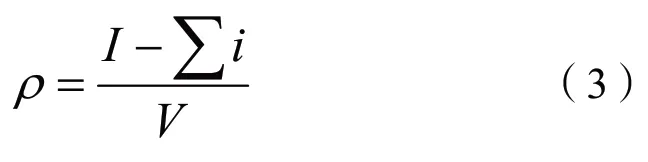
式中：

Ρ为沉箱定倾半径（m）；

I为沉箱浸水面对应断面对其截面形心轴的惯性矩（m4）；

i为第i箱格内压载物的水平面对其指定截面形心轴（平行于沉箱的计算形心轴）的惯性矩（m4）。

V为沉箱的排水量（m3）。

由公式（1）、（2）和（3）可以看出，要计算沉箱的浮游稳定性，需要计算出沉箱的诸多几何属性参数，如沉箱的体积、重心、水平截面的面积及形心、各箱格的面积及形心，以及最小的定倾半径等，其中，计算沉箱的最小定倾半径，需找出沉箱浸水面对应断面对其截面形心轴的最小惯性矩和对应的截面形心轴位置（即为沉箱浮游时的转动轴），以及各箱格截面对其指定截面形心轴（平行于沉箱的计算形心轴）的惯性矩。

对于常规的矩形沉箱，上述各参数的计算较为简单，简单的手算即可得出，其水平截面最小惯性矩对应平行于长边的形心轴。但是对于异型沉箱，若采用手算方法计算上述各参数，计算过程相当繁琐，但采用AutoCAD 建立三维模型，则可方便快捷地解决该问题。

2 求解截面的最小惯性矩

2.1 转轴公式

对于任意截面，当坐标系发生旋转时，各坐标系下的截面惯性矩和惯性积之间存在一定的相关性，材料力学中称之为转轴公式[5]，具体如下：

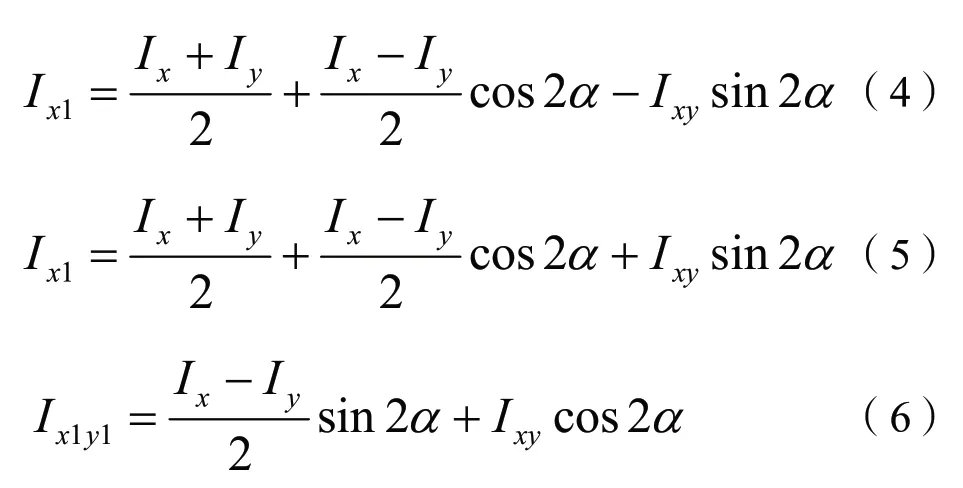
式中：

Ix、Iy、Ixy分别为对于截面内任意一个坐标系xOy，该截面对应坐标轴x，y的惯性矩和惯性积；

Ix1、I1y、Ix1y1分别为对于坐标系xOy 绕其原点O 逆时针旋转α角得到的新坐标系x1Oy1，该截面对应新坐标轴x1，y1的惯性矩和惯性积。

2.2 惯性矩圆

联立公式（4）、（6）及（5）、（6），可分别得到：

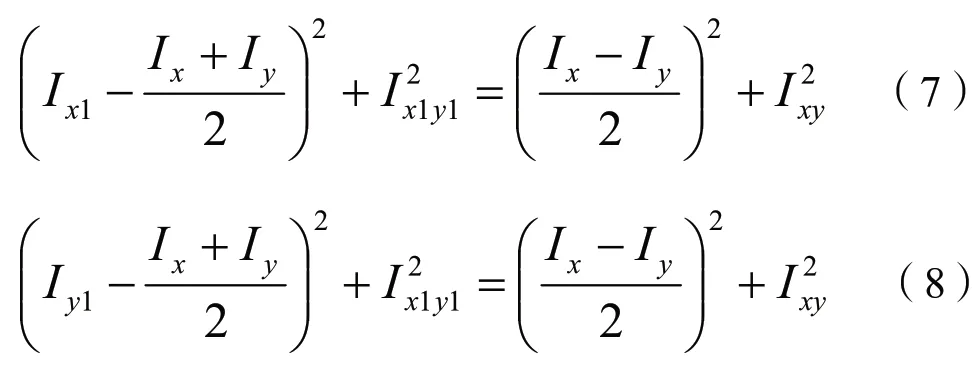
可以看出上式符合圆的解析表达式。对于截面内任一坐标系xOy，该截面对应坐标轴x，y的惯性矩和惯性积分别为Ix、Iy和Ixy，分别以惯性矩、对应的惯性积为横、纵坐标，以（，0）为圆心、半径，得到的圆形可称为惯性矩圆，如图2 所示。由公式(7)和(8)可知，惯性矩圆中任一直径的两个端点均对应一组在新坐标系（由原坐标系xOy 绕其原点O 旋转所得）下的惯性矩和惯性积。

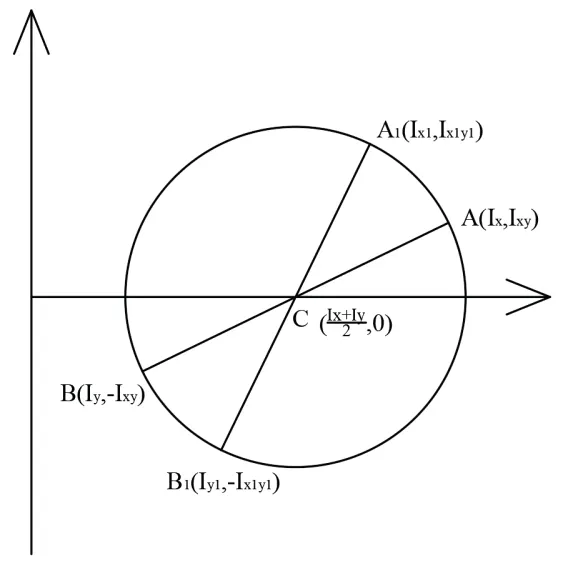
图2 惯性矩圆

2.3 惯性矩和惯性积在惯性矩圆上的相互关系

在惯性矩圆中，假定已知坐标系xOy 下对应坐标轴x，y的惯性矩（Ix、Iy）和惯性积（Ixy）对应的直径AB 与横坐标轴之间的夹角为2α0，将直径AB 逆时针旋转2α角，可得一条新的直径EF，其对应的端点坐标分别为点E（）、F，如图3 所示。

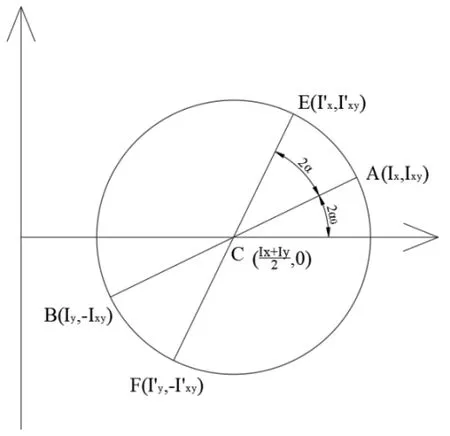
图3 惯性矩圆中惯性矩（积）间的关系示意

根据图3 得：

对比公式（4）、（5）和（6）可得：

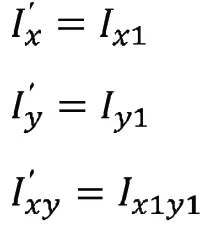
根据上述分析可得，在惯性矩圆上，由已知坐标系xOy 下对应坐标轴x，y的惯性矩（Ix、Iy）和惯性积（Ixy）绘制一条直径，将其绕惯性矩圆的圆心C 点逆时针旋转角度2α，所得新直径的两个端点坐标即为截面对于原坐标系xOy 绕O 点逆时针旋转α 角所得新坐标系x1Oy1的惯性矩和惯性积。

2.4 利用惯性矩圆求解截面最小惯性矩

观察惯性矩圆可以看出，其水平直径对应的惯性矩一个最小、一个最大。根据上一节的分析可知，此时对应的坐标系x’Oy’可由已知坐标系xOy 绕O点顺时针旋转角度a0得到，a0可由以下公式计算：

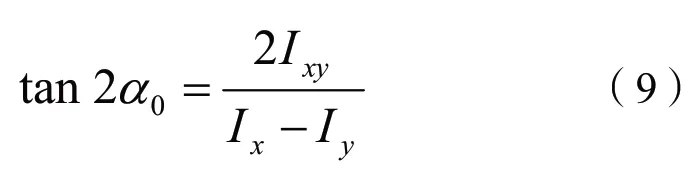
由此，可以得出对于截面内通过点O 的所有坐标系，截面在坐标系x’Oy’下的惯性矩和为大小极值，其数值可由以下公式求得：

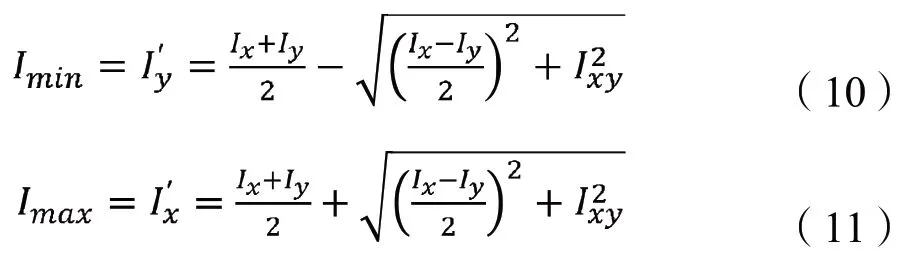
根据惯性矩的平行轴定理可知，对于截面内所有相互平行的坐标轴，截面对形心轴的惯性矩为最小。结合上述分析，如将坐标系xOy 的原点O 建立在截面形心上，则可通过公式(10)计算出截面的最小惯性矩。

2.5 非对称截面沉箱浮游稳定的计算步骤

基于上述理论分析，下文将介绍依托项目中计算横截面不对称的异型沉箱浮游稳定的具体步骤。

1）绘制异型沉箱的水平截面A1（由外轮廓线生成），利用AutoCAD 中的查询功能（命令Massprop）读取截面A1 的形心，在截面A1 内以其为原点建立任意坐标系x0Oy0，如图4，同时读取截面A1 在坐标系x0Oy0下对应坐标轴x0和y0的惯性矩和惯性积、以及截面面积A[6]。

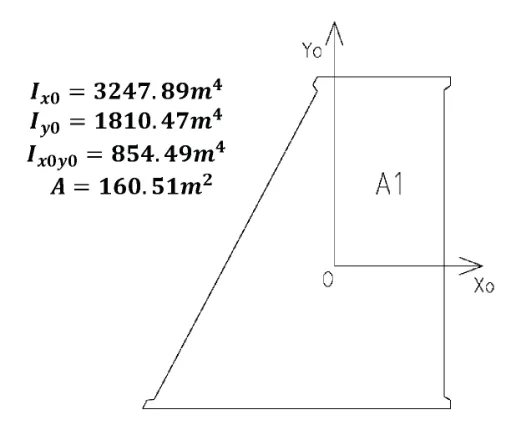
图4 截面A1 内任意坐标系x0Oy0

2）利用公式（9）计算截面A1 的最小惯性矩所对应的坐标轴位置，由坐标系x0Oy0绕坐标原点O 顺时针旋转角度a0可得，从而建立新的坐标系xOy，如图5 所示。

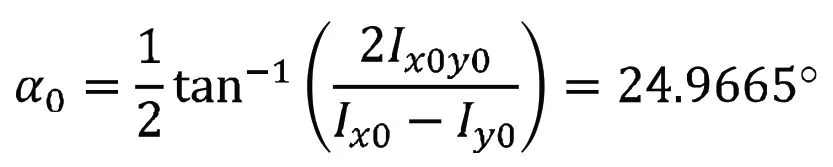
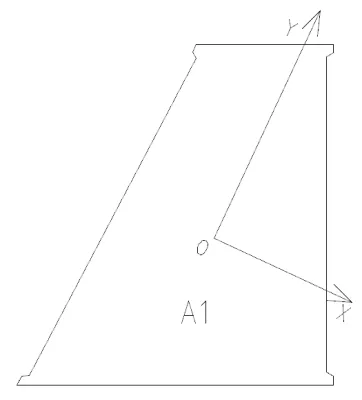
图5 截面A1 的最小惯性矩对应的坐标系xOy

3）利用公式（10）计算截面A1 的最小惯性矩。

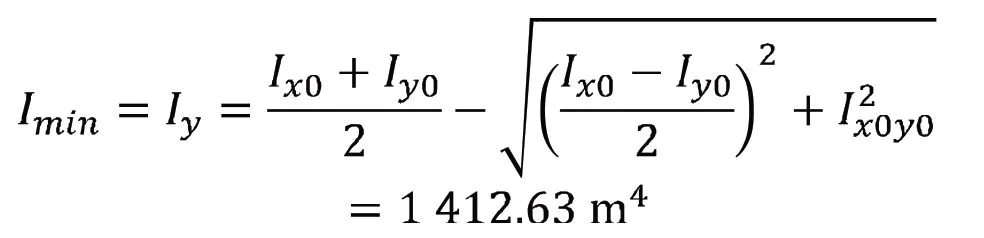
4）在截面 A1 中绘制各箱格的水平截面C1-C10，如图6 所示。先在CAD 中读取截面C1-C10 在新建坐标系xOy 下的形心位置（xi，yi）以及其对于y轴的惯性矩，然后利用平行轴公式求解各截面对于其自身平行于y轴的形心轴的惯性矩（Ii）。

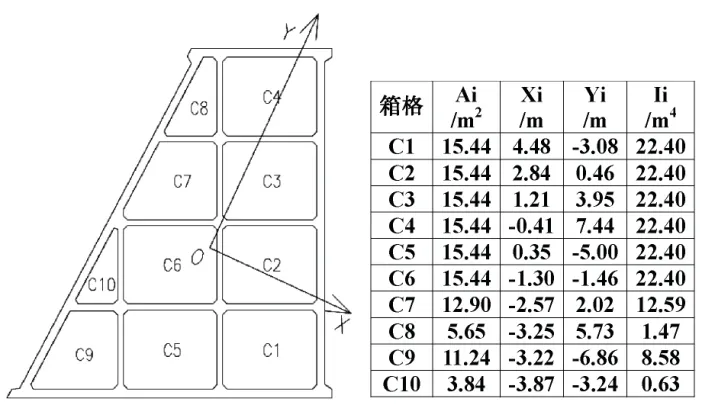
图6 各箱格在坐标系xOy 中的位置及几何参数

5）建立沉箱的三维模型[6]，在沉箱顶面以其截面形心为原点建立三维坐标系xyz，其中x轴和y轴的方向与第2 步中新建坐标系xOy 的坐标轴方向一致，z轴为沉箱高度方向，向上为正。在AutoCAD 中利用查询功能（命令Massprop）可快速读取沉箱的体积和重心位置等几何属性参数。

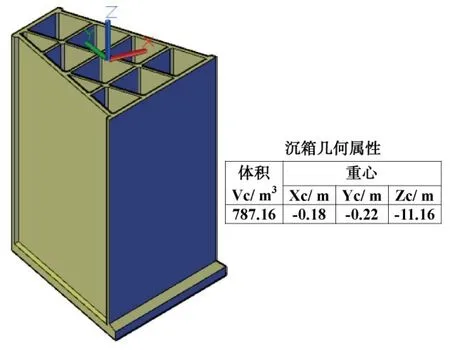
图7 沉箱的三维模型及几何属性

6）假定各箱格内的压载水高度为hi，采用Excel建立各数据间的相关性方程[7]，具体如下公式（12）～（16）。本文所研究的异型沉箱，扣除前趾和侧趾，其在竖直方向上为等截面结构，因前趾和侧趾的体积相对较小，其对浮心位置的影响可忽略不计，因此，可认为沉箱在水平状态下的浮心在浸水面上的投影与浸水面的形心重合[8]，即在坐标系xyz中，浮心的x、y坐标值均为0。

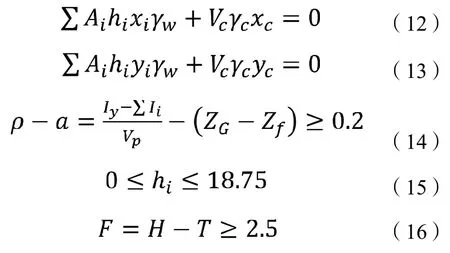
式中：

VP为沉箱加压载水后的排水体积（m3），

ZG为沉箱加压载水后，其重心在z轴上的坐标值，

Zf为沉箱加压载水后，其浮心在z轴上的坐标值，

H为沉箱高度（m）；

T为沉箱加压载水的吃水（m），

F为沉箱浮运时的干舷高度（m），对于本次计算的异型沉箱，依据规范[4]计算，干舷高度应不小于2.5 m。

对于沉箱内隔板，浮运期间的水头差是其承受的主要荷载，因此在确定箱格内压载水高度时需控制相邻箱格间的水位差，以保证内隔板的结构安全。

将公式（12）～（16）作为约束条件，hi作为求解变量，各相邻箱格间的水位差最小为设置目标，利用Excel 自带的规划求解功能，即可快速求出满足条件的hi值，本项目的结果如表1。

表1 计算所得浮游稳定性参数

本项目参照上述数据进行了两个异型沉箱的浮运施工，各箱格压载水高度的理论计算值与现场实施数值基本一致，两个沉箱均顺利完成浮运安装。

3 结语

对于异型沉箱，因水平截面的非对称，其几何属性的计算较为繁琐，难以采用手算的方法快速求解，这也异型沉箱浮游稳定计算的难题。在依托项目中，通过理论分析，并借助相关工具，提出了一种简便高效的解决方法：先利用转轴公式和惯性矩圆的相关理论，求解截面的最小惯性矩及对应的形心轴；再采用AutoCAD 建模求解异型沉箱的几何属性；最后，运用Excel 的规划求解功能进行数据相关性分析，求解各箱格内所需的压载水高度。上述方法可高效快捷地解决异型沉箱浮游稳定计算的难题，希望可为类似工程提供借鉴，推进沉箱结构在水运行业的进一步发展应用。