结合特征扰动与分配策略的集成辅助多目标优化算法

刘子怡，王宇嘉，孙福禄，贾 欣，聂方鑫

（上海工程技术大学电子电气工程学院，上海 201620）

0 概述

在科学研究及工程应用中存在很多多目标优化问题（Multi-objective Optimization Problem，MOP）［1-2］，且这些优化问题呈现出规模越来越大、复杂性越来越高的特征。进化算法是一种模拟自然进化过程的随机优化算法，采用群体搜索策略，无需分析目标函数或约束，单次运行即可获得一组非主导的解，适用于求解多目标优化问题［3］。但是多数多目标进化算法通常需要上万次适应度评估才能得到令人满意的解［4］，比如进气通风系统设计问题需要计算流体动力学模拟来优化目标，一次适应度评估就需数小时，整体评估则需耗费几小时甚至几天［5］，因此此类多目标优化问题通常被称为昂贵多目标优化问题［6］。

近年来，针对昂贵多目标优化问题，CHUGH 等［7］提出一种采用代理模型替代部分昂贵评估的方法，能够有效解决计算开销大的问题。还有一些研究人员分别将径向基函数网络（Radial Basis Function Network，RBFN）［8］、支持向量回归（Support Vector Regression，SVR）［9］、Kriging［10］和人工神经网络（Artificial Neural Network，ANN）［11］用于求解非线性问题。LI 等［12］结合自我改进的新预筛选策略提出一种RBF 辅助的多种群协同进化算法。LIU 等［13］提出一种置信下界辅助的差分进化算法，该算法在优化过程中使用Kriging 代理模型在候选后代粒子群中筛选粒子。TIAN 等［14］提出一种高斯过程（Gaussian Process，GP）辅助的进化算法，该算法采用多目标填充准则的方式选择真实适应度评估的个体。然而，随着决策变量维数的增加，构建Kriging代理模型的计算成本成指数级增加，且单一代理模型只能解决少数问题，评估精度与多样性较差。

为提高代理模型的质量与多样性：GOEL 等［15］提出一种结合多个代理模型的模型集成方法，在集成过程中个体的准确性与多样性达到适当平衡时，可提供比单个模型更高的预测准确率；TANG 等［16］提出一种基于二次多项式模型和RBFN 组成的混合全局代理模型的代理辅助进化算法；WANG 等［17］使用Kriging、PR和RBFN 不同代理模型集成了全局与局部模型，强化算法搜索性能并辅助低维优化；HABIB 等［18］使用Kriging、RBFN 和两种不同功能的RSM 代理模型对每个目标进行近似，并在昂贵多目标优化问题上进行了验证；ROSALES-PÉREZ 等［19］结合模型选择策略确定SVR 超参数，集成一组SVR 代理模型解决多目标优化问题。值得注意的是，在模型管理中采样不确定的个体可有效地提高模型质量，并促进搜索空间中潜在有前途区域的探索［17］。Kriging 代理模型可为每个解提供近似的不确定信息，还能通过集合成员输出之间的方差提供不确定信息，但以上有关集成代理模型方面的研究专注于提高集成的近似评估准确性，忽略了集成过程中的不确定信息［15］。

为利用不确定信息构造准确性较高的代理模型，本文提出一种基于扰动与记忆的集成辅助多目标优化（Ensemble-Assisted Multi-objective Optimization based on Disturbance and Memory，EAMO-DM）算法。该算法对训练集进行特征扰动产生新数据集并共同训练RBFN 和SVR 代理模型，生成多样性强且准确性高的集成代理模型，在适应度评估次数有限的情况下找到较好解，同时在模型管理中通过考虑不确定信息以更好地平衡种群多样性与收敛性。

1 相关技术

1.1 多目标优化

多目标优化函数表示如下：

其中：x=(x1，x2，…，xD)为决策变量，D为决策变量维数；M为目标数量；Ω为可行的决策空间；RM为目标空间。由于多个目标彼此冲突，因此通常存在一组最佳折衷解决方案。在目标空间中，由最佳折衷解（称为Pareto 最优解）形成的图像称为Pareto 前沿（Pareto Front，PF），D中相应的解构成的集合称为Pareto 最优集。

1.2 代理模型

RBFN 代理模型在代理辅助进化算法中具有较强拟合能力，可用于构建局部或全局代理模型，建模计算成本低，问题维度的增加对其拟合效果影响较小［8］。RBFN 是具有单个隐藏层的前馈神经网络，结构由输入层、隐含层和输出层组成。给定i个训练样本xi={xi，1，xi，2，…，xi，n}，RBFN 代理模型表示如下：

其中：τ={τ1，τ2，…，τn}为RBFN 输出权重；||·||表示样本x与RBFN 函数中心ci的欧氏距离；φ(·)为径向基核函数。常用的核函数有高斯、线性、多重二次曲面和立方等核函数［20］。

SVR 代理模型是一种基于支持向量机的机器学习模型，计算成本低且泛化能力好，对小样本问题也有较好的拟合能力［9］。给定i个训练样本xi={xi，1，xi，2，…，xi，n}，SVR 问题可看作如下优化问题：

其中：ω为超平面法向量；b为偏置项。SVR 的优化目标为最小化训练样本与不敏感损失函数ε之间的误差，获得最优超平面，使预测偏差最小化［9］，具体如下：

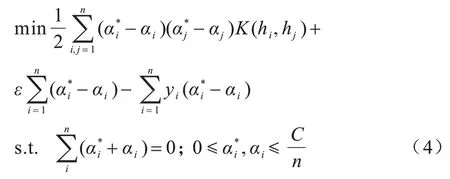
其中：α与α*为拉格朗日乘子；C为惩罚参数，即超出ε的程度；K(hi，hj)为核函数。SVR 代理模型表示如下：

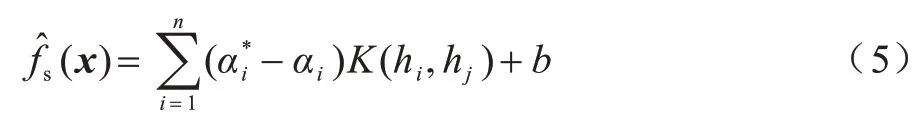
1.3 粒子群优化算法

粒子群优化（Particle Swarm Optimization，PSO）算法是一种基于鸟群的群智能优化算法［21］。在PSO中，搜索空间上的一个粒子为一个潜在解，每个粒子的速度决定其飞行方向和位置，所有粒子跟随当前最优粒子在解空间中搜索，每个粒子的速度和位置计算如下：

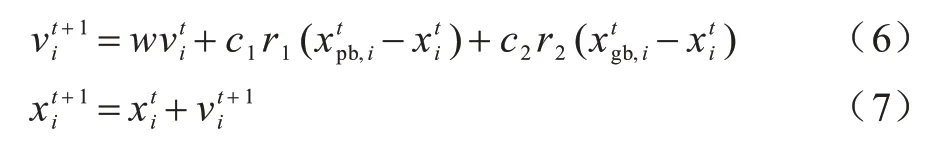
2 基于扰动与记忆的集成辅助多目标优化算法

2.1 基于扰动与记忆的集成代理模型构建

机器学习相关理论证明集成模型中个体的准确性与多样性达到适当平衡时，可以提供比单个模型更精准的预测结果［22］。因此，本文对数据样本引入特征扰动，使模型间样本数据不同，以提升集成个体间的多样性，在模型融合过程中加入基于记忆的影响因子分配策略，以提高集成的准确性。

2.1.1 特征扰动

采用主成分分析（Principal Component Analysis，PCA）［23］对种群引入特征扰动，生成全新的样本集。PCA是机器学习中广泛使用的数据处理方法，计算成本低、简单易行，主要思想是在减少数据集维数的同时保留最主要的特征，具体步骤如下：

1）给定初始样本集X={x1，x2，…，xi}，设新生成的样本集Z={z1，z2，…，zi}，对i个样本组成的矩阵X进行零均值化处理，得到样本协方差矩阵：

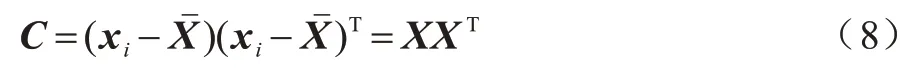
2）对XXT进行特征值分解，求得对应特征值降序排列，并取前l行构成降维后目标矩阵G=(g1，g2，…，gl)，则新生成的样本可表示如下：

3）在使用PCA 对种群进行处理后，得到一组新训练数据，两组数据共同用于训练不同模型。

2.1.2 基于记忆的影响因子分配策略

集成模型中的融合策略用于平衡不同基模型的输出，削弱不完美模型的影响，确保代理预测精度［15］。为提高集成预测的精确度，结合集成模型中各代理的预测输出值，提出一种基于记忆的影响因子分配策略，具体定义如下：

其中：f′(x)为集成对粒子x进行近似适应度评估的结果；Ns为集成中的基代理个数；fi′(x)为集成中第i个代理的预测结果；Ii为fi′(x)的影响因子。Ii定义如下：

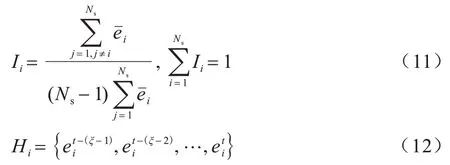
基于记忆的影响因子分配策略的具体步骤如下：

1）更新Hi。当t≤ξ时，只执行存入操作；当t>ξ时，则执行存入与淘汰操作。

2）根据式（12）求取Hi内存储的RMSE 的均值。

本文在对基模型预测结果进行融合的过程中加入基于记忆的影响因子分配策略，误差小的代理模型被分配的权重大，有效避免了代理模型在采样数据点处表现良好但在未勘探区域表现较差而引起的误差，保证了集成稳定性，提高了算法准确性。

2.1.3 集成代理模型构建

结合特征扰动与分配策略的集成代理模型构建如图1 所示。

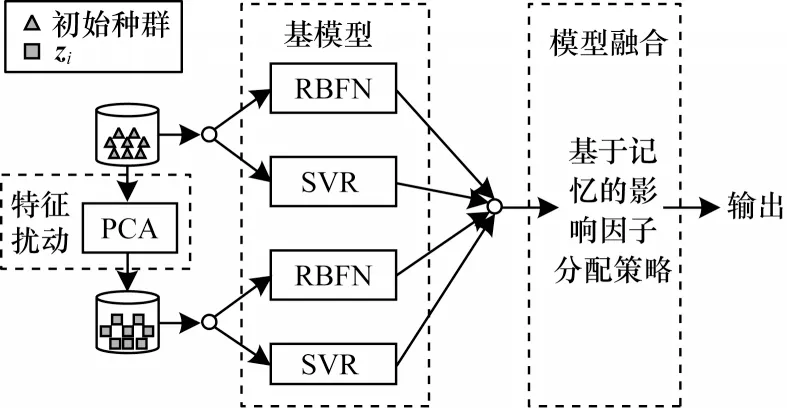
图1 EAMO-DM 算法中集成代理模型的构建Fig.1 Construction of ensemble surrogate model in EAMO-DM algorithm

在集成过程中的基模型选用RBFN 代理和SVR代理，其中：RBFN 模型建模计算成本低，非线性拟合能力强，在高维搜索空间也有很好表现；SVR 模型在小样本问题上占据优势，模型简单并且在中低维搜索空间表现出良好的泛化能力。因此，在集成代理模型构建过程中，将特征扰动及影响因子分配策略分别应用于模型训练和模型融合，结合RBFN 模型与SVR 模型的优势，提高了集成预测的准确性，更好地逼近不同形态的Pareto 前沿并具有高维可拓展性。集成代理模型构建步骤具体如下：

1）使用特征扰动方式对训练集S进行处理得到新训练集S′。

2）使用经过处理的数据集和初始数据集训练RBFN 和SVR 代理模型。

3）结合影响因子分配策略将两代理模型组合成集成代理模型。

4）输出集成预测结果。

2.2 基于不确定信息的加点准则

通过增加采样点可提高模型准确性，但这一过程因其随机性浪费了计算资源。为提升模型精度同时节约计算成本，采用基于不确定信息的加点准则，用于选择个体进行昂贵适应度评估，并将其加入训练集更新模型。在EAMO-DM 算法中，训练集S中的数据用于构建集成，并通过以下策略管理训练集S：采用Kriging 辅助进化算法中广泛使用的置信下界准则［13］将最小LCB 值作为目标，选择最优的个体进行昂贵适应度评估，并放入训练集S中更新集成代理。LCB 评价函数表示如下：

2.3 算法步骤

EAMO-DM 算法的具体步骤如下：

1）使用拉丁超立方设计方法，采样种群规模为N的初始种群，以保证初始种群均匀分布。使用真实函数评估样本点（即计算其对应目标函数值），将非支配解存入外部档案A，更新训练集S。

2）初始化种群中粒子的速度和位置。

3）进入循环，用S和S′中的样本点作为训练数据，针对各目标函数构建集成代理模型。

4）使用多目标粒子群优化算法进行种群更新，利用集成代理对各粒子进行近似适应度评估，筛选用于真实函数评估的个体，评估后放入训练集S更新集成代理。

5）更新各粒子的个体极值、全局极值以及外部档案A，输出Pareto 最优解集。

在EAMO-DM 算法运行过程中，训练集S存放真实函数评估的所有个体，并作为构建或更新集成代理的训练数据集。

2.4 算法复杂度分析

EAMO-DM 算法的计算复杂度T由真实适应度评估次数F、构建集成代理模型TE以及其他额外成本Tother的计算时间确定，具体公式如下：

其中：γ为适应度评估系数。在构建集成模型的过程中，通过特征扰动处理训练样本的计算复杂度为O(λM)，对各代理进行影响因子分配时的计算复杂度为O(λM)，训练RBFN 代理与SVR 代理的计算复杂度均为O(λ2M)，λ为构建代理模型的样本数量，在产生新种群以及选取真实评估粒子过程中的计算复杂度为O(NM)，N为初始种群规模。因此，EAMODM 算法的计算复杂度为O(λ2M)+O(γF)。对于昂贵多目标优化问题，真实适应度评估相当耗时，构建模型所需的时间可忽略不计。

3 实验设计与结果分析

将ZDT 系列测试函数作为多目标优化测试问题，如表1 所示。在EAMO-DM 算法框架中，使用SMPSO［24］作为多目标粒子群优化算法，称为EASMPSO；将EA-SMPSO 算法框架中的集成代理模型替换成单个Kriging 模型，称为K-SMPSO；将EAMO-DM 算法与SMPSO［24］结合，称为EA-SMPSO；将单个Kriging模型与SMPSO结合，称为K-SMPSO。使用EA-SMPSO 与SMPSO、NSGAII［25］、MOEA/D［26］以及K-SMPSO 进行实验对比。

表1 多目标优化测试问题设置Table 1 Setting of multi-objective optimization test problems

3.1 参数设置与性能指标

3.1.1 参数设置

为保证公平性，每种算法进行20 次独立实验，评估次数设为1 000。对于每个测试问题，目标数量M为2，种群规模为50；对ZDT1～ZDT3 测试问题，决策变量维数D为5、10、20；由于ZDT4 及ZDT6 默认决策变量维数有限，决策变量维数D为10。按照文献［27］，将式（12）中参数ξ设为5、式（13）中参数μ设为2。值得注意的是，EA-SMPSO 与K-SMPSO 使用相同的模型管理策略。

3.1.2 性能指标

选用GD、SP、IGD 3 个指标定量评价算法性能：

其中：ψ为P中解的数目；dis为P中个体函数值与中最近个体之间的欧氏距离。GD 越小，解集收敛性越好。

2）SP 指标用于评价算法多样性，其值由最邻近距离的方差表示，计算公式如下：

其中：di是解集中两相邻个体的欧氏距离；为di的均值。SP 越小，解集分布性越好。

3）IGD 指标可用于综合评价解集的综合性能，即收敛性和多样性，计算公式如下：

3.2 实验结果对比分析

实验从性能指标、Pareto 前沿逼近效果以及算法运行时间三方面对比EA-SMPSO 与K-SMPSO、NSGAII、SMPSO 及MOEA/D 在求解ZDT 系列测试问题上的性能表现。

3.2.1 性能指标对比分析

经实验得到各种算法GD、SP、IGD 指标平均值与标准差，如表2～表4 所示，其中最优结果加粗显示。

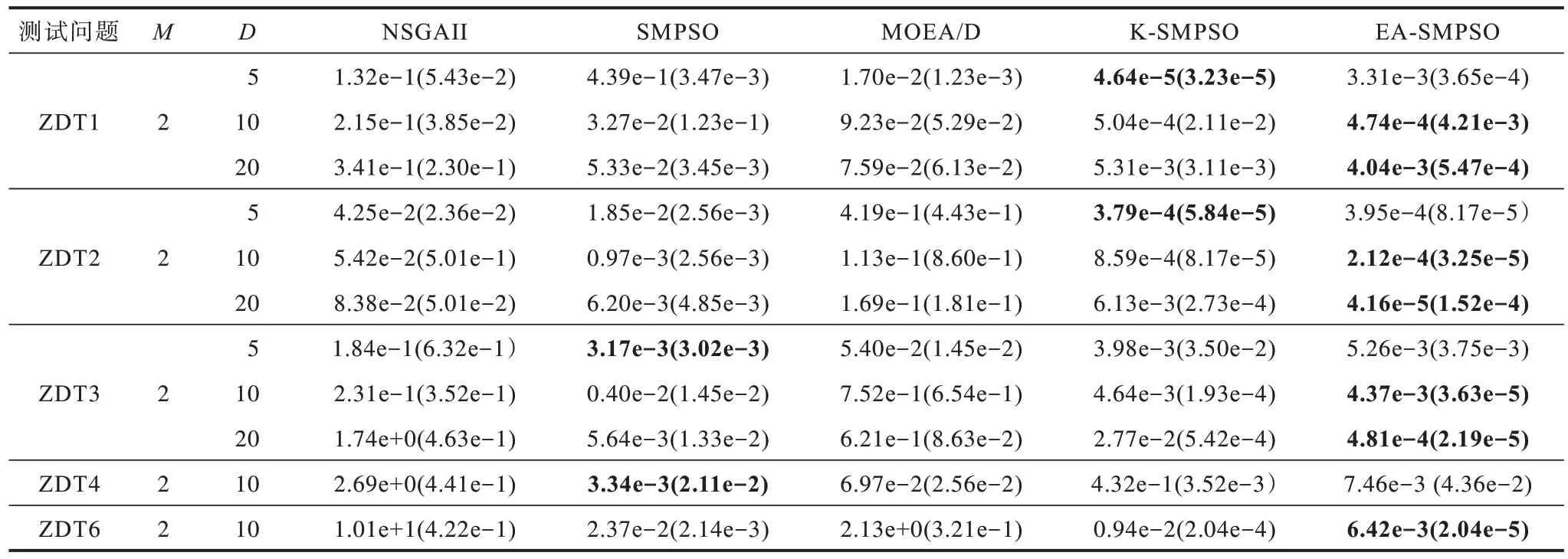
表2 5 种算法GD 性能指标的平均值和标准差Table 2 Average and standard deviation of GD performance indicators of 5 algorithms

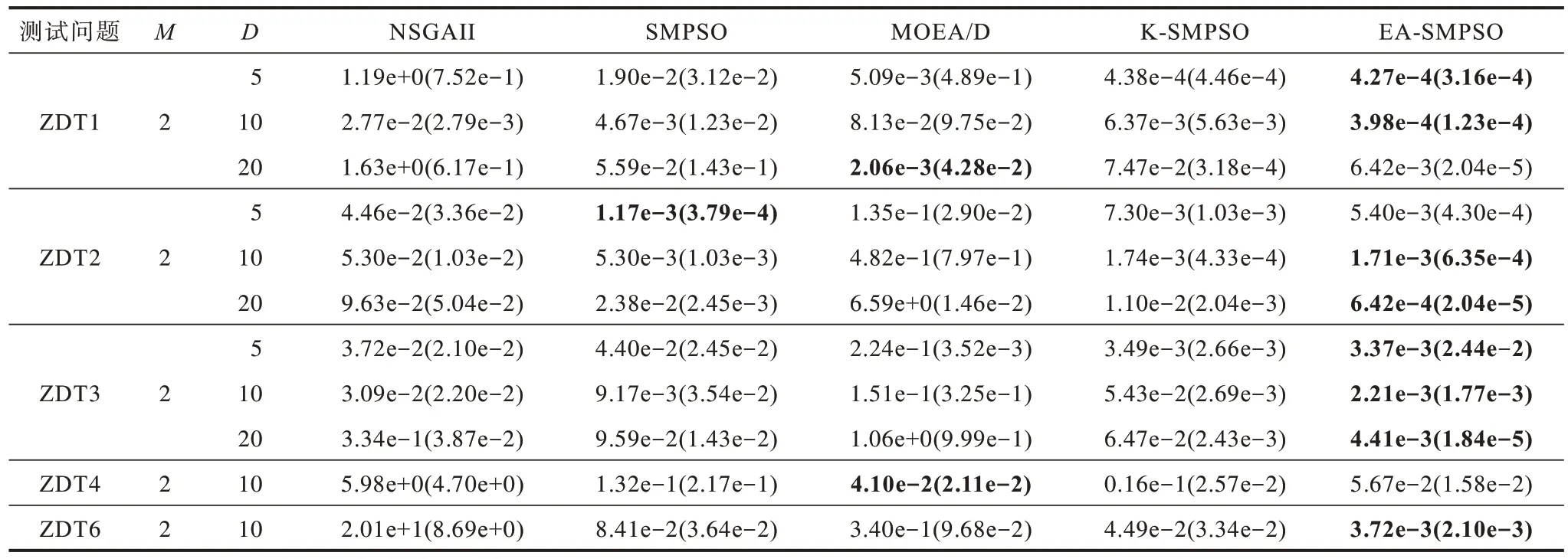
表3 5 种算法SP 性能指标的平均值和标准差Table 3 Average and standard deviation of SP performance indicators of 5 algorithms

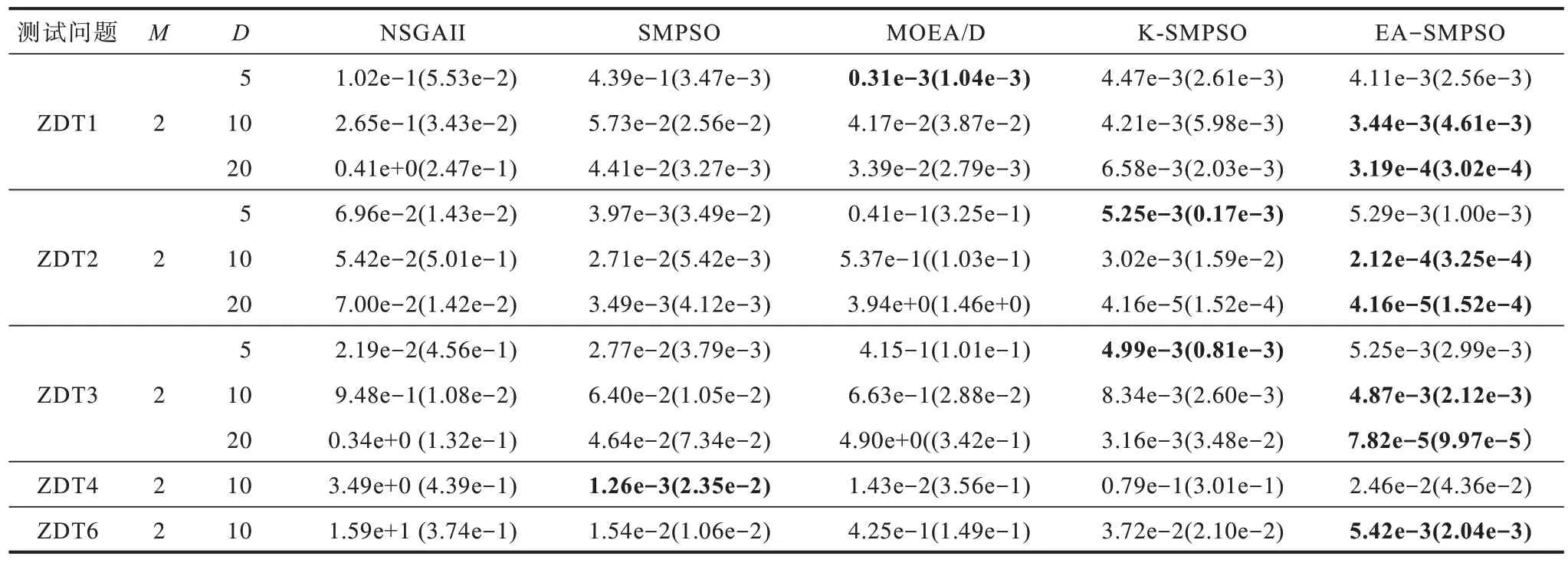
表4 5 种算法IGD 性能指标的平均值和标准差Table 4 Average and standard deviation of IGD performance indicators of 5 algorithms

由表2～表4 可以看出：

1）在决策变量维数为5 的ZDT1、ZDT2 测试问题上，EA-SMPSO 与单个Kriging 辅助的K-SMPSO相比，GD 值稍差（在ZDT2 测试问题上相差不到0.01）；在决策变量维数为10 的复杂ZDT3、ZDT4 测试问题及不均匀的ZDT6 测试问题上，EA-SMPSO的GD 值比K-SMPSO 更好；在决策变量维数为20 的ZDT 测试问题上，EA-SMPSO 在各指标上优势明显。这是算法使用不同的代理模型所致，Kriging 代理模型能对低维非线性问题进行更精确的拟合，RBF 与SVR 代理模型更擅长处理高维小样本问题。

2）在ZDT1～ZDT3测试问题上，随着决策变量维数的增加，EA-SMPSO的SP值较K-SMPSO优势更明显。这表明EAMO-DM 算法的多样性更好，同时探索能力更好，并且验证了Kriging 模型在高维问题上存在对于不确定信息估计不准确的问题［13］，导致算法勘探能力下降。

3）对于不同决策变量维数下的ZDT 测试问题，EA-SMPSO 相比于没有代理辅助的SMPSO、NSGAII及MOEA/D，在ZDT1～ZDT3 测试问题上各指标均更具优势，但在ZDT4 测试问题上GD 值与SP 值稍逊于SMPS 与MOEA/D，这是由于ZDT4 测试问题有多个局部Pareto前沿，多模态特征使得其用集成代理难以近似。

可见，EA-SMPSO 相比于K-SMPSO、NSGAII、SMPSO 及MOEA/D 搜索所得解集的收敛性与分布性更好，综合优势明显。

为进一步分析多目标优化算法的有效性，以ZDT1～ZDT3 测试问题为例，给出EA-SMPSO、K-SMPSO、SMPSO 的IGD 指标变化趋势，如图2 所示。从图2 可以看出：SMPSO、K-SMPSO 与EA-SMPSO 的IGD 值都随评估次数增加较为平稳下降。虽然K-SMPSO 与EASMPSO 均能收敛到较好指标，但集成代理辅助条件下指标下降更快，因为EA-SMPSO 比单个Kriging 代理更为精确，能更快地搜索到更好的解，同时验证了集成代理提供的不确定信息的有效性。另外，对于相同IGD指标，EA-SMPSO 与SMPSO 相比，使用集成代理的EA-SMPSO 约减少90%的评估次数，这对于昂贵多目标优化问题具有重要意义。

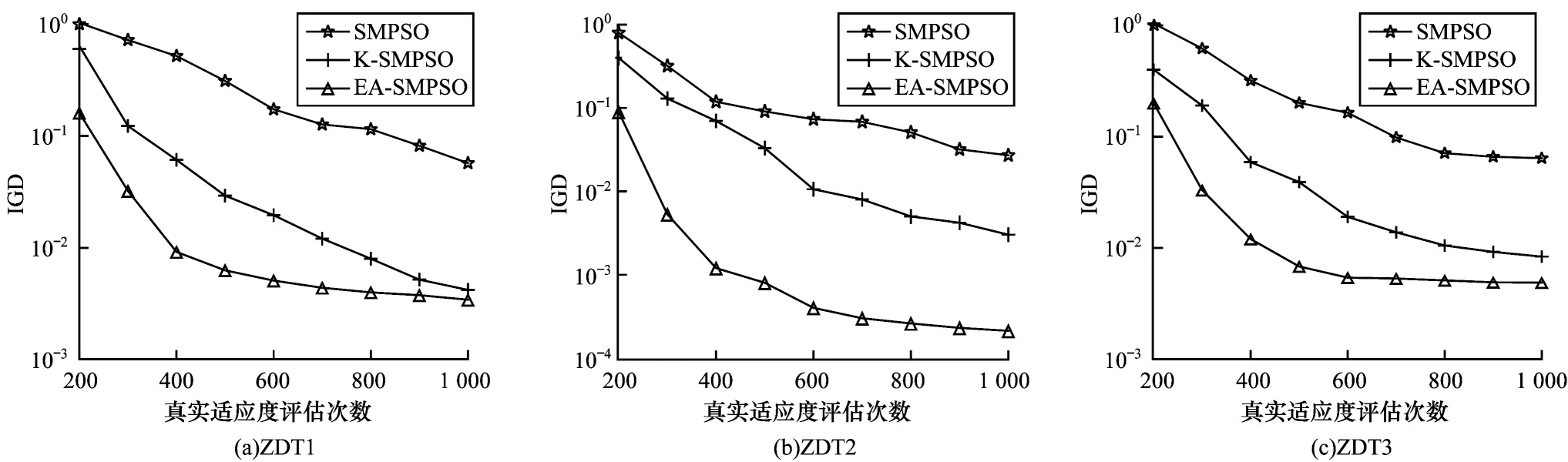
图2 EA-SMPSO、K-SMPSO 和SMPSO 算法求解ZDT1～ZDT3 测试问题时的IGD 指标变化趋势Fig.2 Variation trend of IGD when EA-SMPSO，K-SMPSO and SMPSO algorithms solve ZDT1～ZDT3 test questions

3.2.2 近似Pareto 前沿对比分析

图3 给出了各算法在求解ZDT 系列测试问题时获得的近似Pareto 前沿，其中f1、f2代表ZDT 系列测试问题中的2 个目标函数值，彩色效果见《计算机工程》官网HTML 版。由图3 可以看出，EA-SMPSO 在ZDT1～ZDT3 以及ZDT6 上逼近效果最好，具有较好的收敛性以及分布性。值得注意的是，ZDT4 是一个具有复杂多模态的测试函数，使用集成模型或者Kriging模型辅助的SMPSO 近似Pareto 前沿的效果稍弱于SMPSO 本身，但对于昂贵多目标优化问题重要的是使用更少评估次数获得更好的解。在ZDT4 测试问题上：MOEA/D 与NSGAII 都无法很好地逼近Pareto前沿，因此不适合昂贵多目标优化问题；EA-SMPSO相比于K-SMPSO 在Pareto 前沿上找到了更多的解，说明集成代理模型相对Kriging 模型在复杂多模态问题上更具优势。

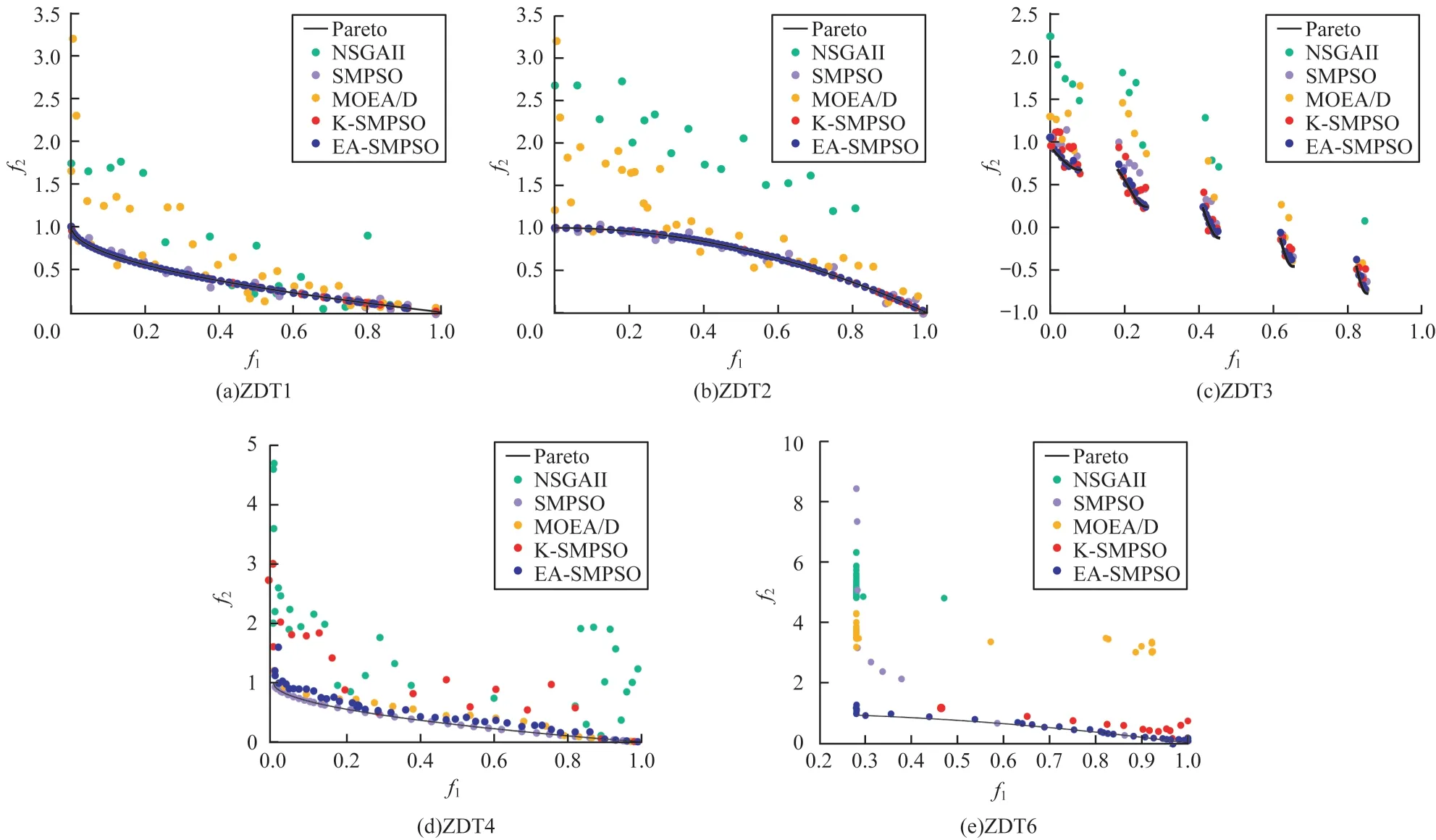
图3 5 种算法求解具有10 个决策变量维数的ZDT1～ZDT4 和ZDT6 测试问题时获得的近似Pareto 前沿Fig.3 Pareto front of 5 algorithms solve the ZDT1～ZDT4 and ZDT6 test questions with 10 decision variable dimensions

3.2.3 算法运行时间对比分析

为进一步分析本文提出的集成代理模型较单个Kriging模型在昂贵多目标优化问题上的优势，对具有5、10、20 个决策变量维度的ZDT 系列测试问题使用EA-SMPSO 与K-SMPSO 分别进行求解，记录其所需的运行时间。如图4所示，随着决策变量维度的增加，KSMPSO需增加采样点保证Kriging模型的精度，计算成本呈指数增加，因此K-SMPSO相比于EA-SMPSO的运行时间增长更快，而EA-SMPSO可使用一组数据构建更为精确的集成模型，加快了寻优速度，节约了计算成本。

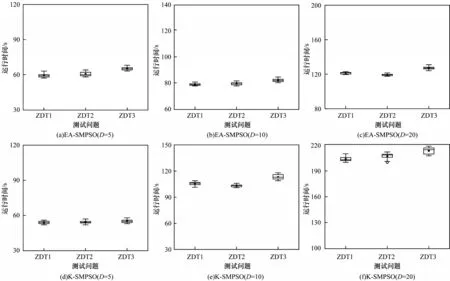
图4 EA-SMPSO 算法和K-SMPSO 算法求解具有5、10、20 个决策变量维数的ZDT1～ZDT3 测试问题的运行时间Fig.4 Running time of EA-SMPSO algorithm and K-SMPSO algorithm to solve the ZDT1～ZDT3 test questions with 5，10，and 20 decision variable dimensions

4 结束语

本文提出一种基于扰动与记忆的集成辅助多目标优化算法，使用RBFN 和SVR 代理模型，并结合特征扰动与影响因子分配策略构建集成代理模型，同时考虑了不确定信息以选择进行适应度评估的个体。实验结果表明，该算法在处理具有凹、凸、非连续、非均匀特性的多目标问题时，得到解集的分布性与收敛性相比经典算法更好，并且当决策变量维数增加时，使用集成代理模型可获得比Kriging 代理模型更准确的预测结果，同时计算成本较低。下一步将设计更高效的模型管理策略，并通过充分利用并行仿真资源，将本文算法应用于求解更多的昂贵多目标优化问题。