基于粒计算的非线性感知机

陈玉明，董建威

（1.厦门理工学院计算机与信息工程学院，厦门 361024；2.易成功（厦门）信息科技有限公司，厦门 361024）

引 言

美国学者Zadeh 指出现实世界存在大量模糊现象之后，1996 年，香港学者Lin［1］首次提出了粒计算理论。粒计算是一种新的知识表示方法，研究事物的多层次、多粒度表示，处理模糊、不确定的信息，而且是人类认知机理的研究范畴［2］。1999 年，加拿大学者Yao［3］提出了基于邻域关系的粒计算，并在知识挖掘领域进行了应用。21 世纪以后，国内众多学者开始关注粒计算领域。Liu 等［4］发表了专著论述粒计算理论，并基于粒计算研发了一个医疗诊断专家系统。苗夺谦等［5⁃7］提出知识的不确定性度量，开创性将信息熵引入粒计算领域。王国胤等［8］讨论了多种粒计算模型及其在数据挖掘中的应用。吴伟志等［9］定义了一种粒结构，并应用于概念格。粒计算能够分析与处理复杂数据，将复杂的对象细粒度分解而求解问题，并广泛应用于机器学习领域［10⁃11］。机器学习属于人工智能领域，是机器通过学习，期望能模拟人类的思维。它从大量的数据中寻找和学习其背后的隐藏规律，从而达到模拟和预测的目的。机器学习应用广泛，在搜索引擎［12］、人脸识别［13］、机器翻译［14］和语音识别［15］等商业领域中均有较好的应用；同时也为学术研究提供了新方法，在生物医学［16］、材料科学［17］、医疗诊断［18］、隐私安全［19］和气象预报［20］等领域均有重要的学术建树。1957 年Rosenblatt［21］提出了感知机模型，它是机器学习与深度学习的理论基础。Novikoff［22］，Minsky 等［23］对感知机进行了理论研究，后续改进的感知机模型包括口袋感知机［24］、表决感知机［25］和带边缘感知机［26］。传统感知机模型具有简单、运算效率高的优点，是神经网络与支持向量机的起源算法，也是构建深度学习模型的基础。然而，传统感知机的非线性数据处理能力较弱，其改进算法中通过引入核函数增强了非线性处理能力，但算法复杂度较高。为了克服感知机非线性处理能力弱的缺点，从粒计算的理论出发，从多个特征角度构造粒子与粒向量，建立一种粒分类器。粒的构造本质上是一种集合，则粒计算是一种集合方式运算。信息粒化是粒计算常用的技术与方法，然而粒化与分类器结合的例子并不多见。以信息粒化为基础，本文提出了一种新型的感知机分类模型—粒感知机。样本在单特征上的粒化形成粒子，多特征上的粒化粒子组成粒向量，从而构造粒感知机模型。进一步设计粒感知机策略，本文提出粒感知机学习模型，讨论粒感知机收敛性。通过设计粒感知机的梯度下降算法，成功实现了基于信息粒形式的数据拟合与预测。最后进行实验分析，验证感知机模型的正确与有效性。

1 感知机的粒化

感知机模型简单、参数较少，难以拟合非线性大数据系统。大数据系统具有量大、高维与非线性的特点。为了更好地处理大数据集，本文对样本进行单特征粒化，形成单特征粒子。1 个样本在某个特征上粒化为1 个粒子，高维特征上进行粒化则构造出这个样本的粒向量。

设感知机系统为U=(X，C，{d})，其中样本集合为X=(x1，x2，…，xn)，条件特征集合为C={c1，c2，…，cm}，d为决策特征；给定单样本x∈X，对于单特征c∈C，v(x，c)∈R 表示样本x在特征c上的值；该样本x对应的决策值为y∈{-1，+1}。

定义1设感知机系统为U=(X，C，{d})，对于样本xi，xj∈X，单特征c∈C，则xi与xj在单特征c上的曼哈顿距离为

定义2给定感知机系统U=(X，C，{d})，对于任一样本xi∈X和任一条件特征c∈C，则xi在特征c上进行粒化，形成的条件粒子定义为

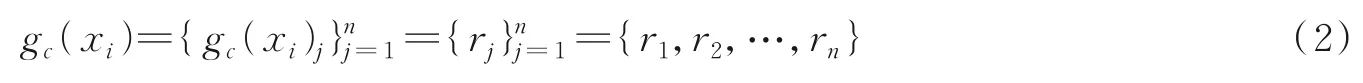
式中rj=sc(xi，xj)表示样本xi，xj在单特征c上的距离。易知sc(xi，xj)∈R，因此rj∈R。粒子由粒核组成，gc(xi)为粒子，gc(xi)j为第j个粒核。

该样本xi对应的决策yi在决策特征d上进行粒化，形成决策粒子，定义为

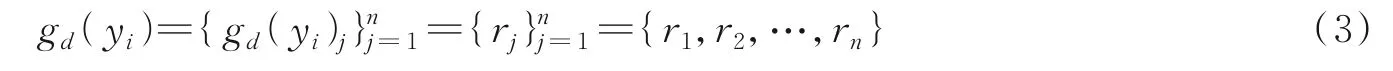
式中rj=1-|yi-yj|。因为yi，yj∈{-1，+1}，易知rj∈{-1，+1}。

感知机系统经过粒化后，形成条件粒子和决策粒子。条件粒子的值是实数集合，决策粒子的值是±1 集合。1 个条件粒子和1 个决策粒子组成1 条粒规则，相应的条件粒核和决策粒核则组成粒核规则。

定义3设U=(X，C，{d})为感知机系统，对于任一样本xi∈X，任一特征子集P⊆C，设P={a1，a2，…，am}，则xi在特征子集P上的粒向量定义为

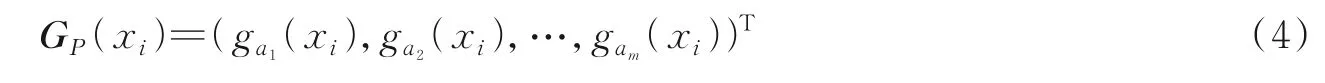
式中gam(xi)为样本xi在特征am上的粒子。为方便算计，特征集P={a1，a2，…，am}用整数标记，则粒向量可表示成G(xi)=(g1(xi)，g2(xi)，…，gn(xi))T。

粒向量由粒子组成，粒子又由粒核构成。因此粒向量可以是一个矩阵的形式，表示为

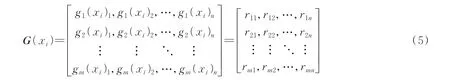
粒向量也可以用粒核向量表示为

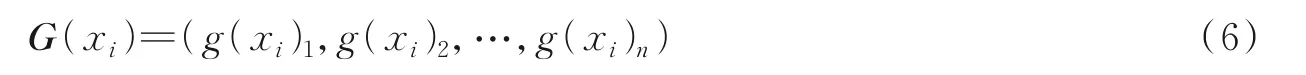
式中g(xi)j=(g1(xi)j，g2(xi)j，…，gm(xi)j)T为粒核向量。

感知机的粒向量GP(xi)由粒子组成，而粒子是1 个集合的形式。因此，粒向量的元素是集合，与传统向量不一样，传统向量的元素是1 个实数。

2 粒感知机模型

输入样本的特征向量，感知机输出样本的类别，它是二分类模型，分类结果是+1 和-1。样本先粒化，然后进行粒的运算，从而形成一种粒感知机模型。其输入为粒向量，输出为只含有±1 的粒子，进而判别样本的类别。粒感知机模型如图1 所示。粒向量是由粒子组成的，粒子是一种含有实数的序列，表示了样本之间的距离度量与复杂结构，因此可拟合非线性模型。

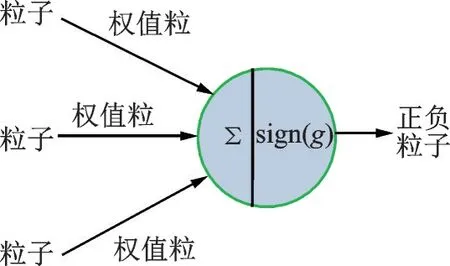
图1 粒感知机Fig.1 Granular perceptron

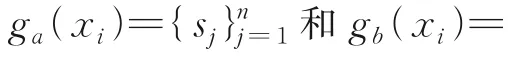
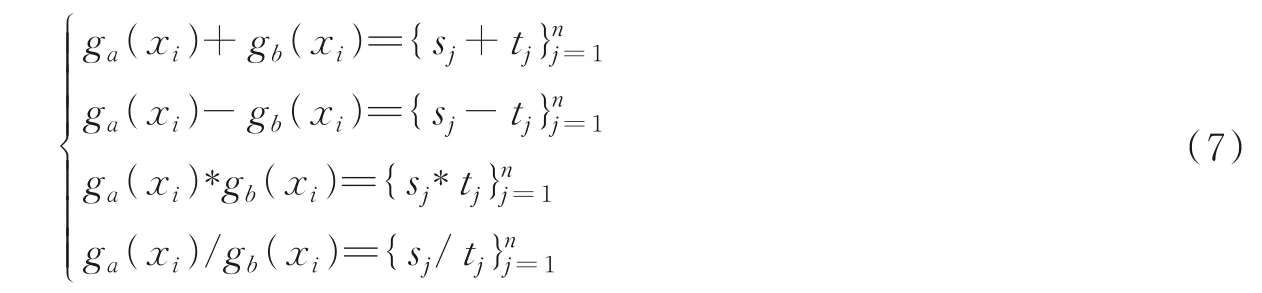
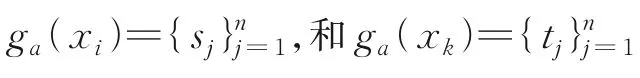
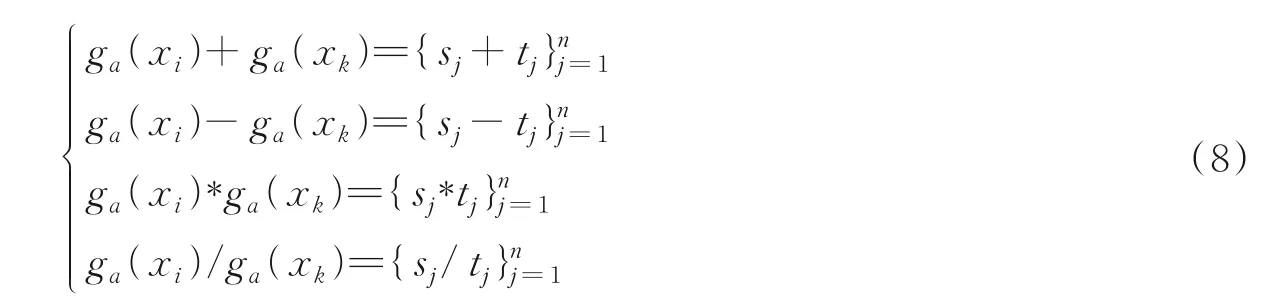
2 个粒子的加减乘除运算结果为1 个粒子。定义4 的定义是针对同一个样本在不同特征集合上粒化为不同粒子的运算，而定义5 则是应用在不同样本在同一特征集合上粒化后粒子的运算。

定义6设U=(X，C，{d})为感知机系统，对于两个样本∀xi，xk∈X，存在其相应的粒向量为G(xi)=(g1(xi)，g2(xi)，…，gm(xi))T，G(xk)=(g1(xk)，g2(xk)，…，gm(xk))T，则这2个粒向量的点乘为

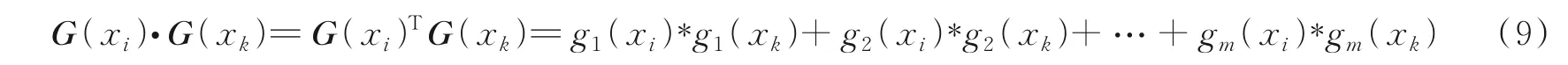
2 个粒向量的点乘结果为1 个粒子。因此，本文可以通过构造1 个权值粒向量，让样本的粒向量与权值粒向量进行点乘运算，其结果也为1 个粒子。

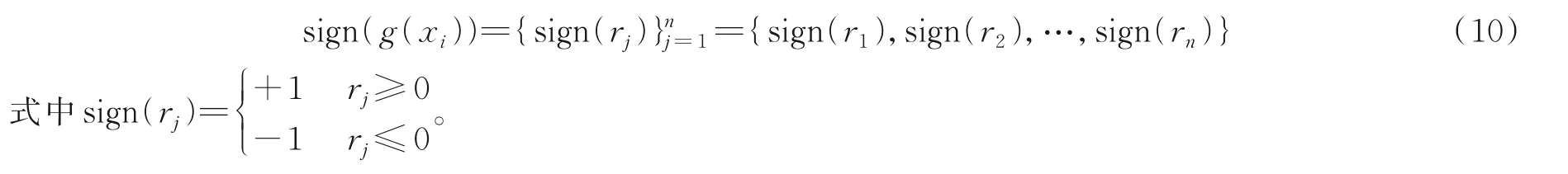
定义8设U=(X，C，{d})为感知机系统，对于样本∀xi∈X，粒向量为G(xi)=(g1(xi)，g2(xi)，…，gm(xi))T，给定权值粒向量W=(w1，w2，…，wm)T和偏置粒子b，则粒感知机表示为

粒感知机是关于粒子的函数，通过样本条件粒向量与权值粒向量的内积计算与sign 函数运算，结果为条件粒子，而且其粒核只含有±1。同时，感知机系统中决策值进行粒化后形成决策粒子，而决策粒子的粒核也是只含有±1。因此，粒感知机系统中的条件粒子与决策粒子进行相乘，其结果为只含有±1 粒子。结果为-1 的粒核则为误分类粒核，将梯度回传修正权值粒核向量，从而形成粒感知机分类器。

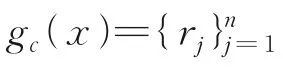
若q(gc(x))＞0，则粒子大小为正；反之，粒子大小为负。

感知机模型的学习训练过程就是优化确定权值粒向量与偏置粒子的值，学习后的感知机模型则可以预测样本的类别。输入样本粒化后，输出粒子，通过度量粒子的大小确定样本的类别。输出结果为正，则判定为正例类别；输出结果为负，则判定为负例类别。

3 粒感知机损失函数与学习算法

为了降低大数据系统的复杂性，本文将1 个样本按照不同的特征粒化为多个粒子，这些粒子组成1个粒向量。同时，该样本的决策值也粒化为只含有±1 的粒子。为了优化粒感知机模型的参数，需要定义粒感知机的损失函数，求取损失函数的导数，从而得到粒感知机的梯度下降学习算法。

3.1 粒感知机损失函数

传统感知机模型是通过找到正确的分类超平面确定模型参数。利用损失函数，监督感知机的分类性能；利用梯度下降法，最后学习到感知机的分类超平面。经典感知机的损失函数为误分类点到超平面的总距离。

在粒感知器模型中，样本已经粒化为粒子。类似于感知机，粒感知机的损失函数为误分类粒子到超平面的总距离。粒子是粒核的集合，误分类粒子是因为其粒核产生了误分类。本文可以计算粒子中误分类的粒核到超平面的距离，此粒子中误分类粒核个体到超平面的距离之和作为该误分类粒子的距离，因此可得到所有误分类粒子到超平面的总距离。

定义11给定训练数据集T={(x1，y1)，(x2，y2)，…，(xn，yn)}，其中xi∈X⊆Rm，yi∈{-1，+1}，i=1，2，…，n。训练集T粒化为GT={(G(x1)，g(y1))，(G(x2)，g(y2))，…，(G(xn)，g(yn))}，其中G(xi)=(g1(xi)，g2(xi)，…，gm(xi))T为条件粒向量，g(yi)为决策粒子。设W=(w1，w2，…，wm)T为权值粒向量，b为偏置粒子。粒感知机的损失函数定义为

式中M为误分类粒向量的集合。

定理1当粒向量G(xi)存在误分类的粒核向量时，g(yi)*(W·G(xi)+b)为负粒子。

证明对于∀xi，W·G(xi)+b结果为粒子。因粒向量G(xi)存在误分类的粒核向量，所以W·G(xi)+b与g(yi)必然存在正负相异的粒核。g(yi)*(W·G(xi)+b)的结果仍然为粒子，也必然存在负的粒核。根据负粒子的定义，可知g(yi)*(W·G(xi)+b)为负粒子。

3.2 粒感知机学习算法

定义粒感知机的损失函数

则参数W，b为下列损失函数极小化问题的解

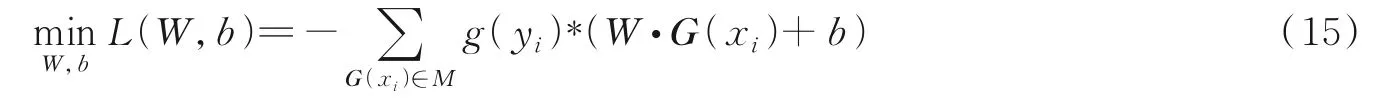
式中M为误分类粒向量的集合。

W·G(xi)为2 个粒向量的点乘，其结果为1 个粒子，则W·G(xi)+b的结果也为粒子。g(yi)*(W·G(xi)+b)为2 个粒子相乘，结果为粒子。因G(xi)为误分类粒向量，则W·G(xi)+b与g(yi)必然存在正负相异的粒核，也必然存在g(yi)*(W·G(xi)+b)为负的粒核，将这些为负的粒核加负号后，则变为正的粒核。

因此，粒感知机学习算法由误分类的粒核驱动，具体实现则采用随机梯度下降法。首先，参数W，b进行初始化，然后利用梯度下降法不断极小化目标函数。其方法是1 次随机选取1 个误分类粒子，按照梯度方向，修正该粒子中误分类的粒核权值。

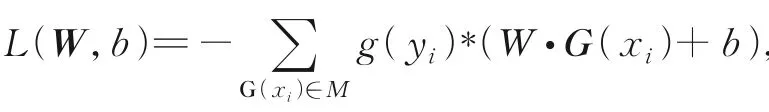
根据上述其导数的相关证明，推导出梯度下降法，进而求解粒感知机的近似最优解。粒感知机算法分为学习算法和分类算法，分别描述如下：

（1）粒感知机学习算法

输入：训练集T={(x1，y1)，(x2，y2)，…，(xn，yn)}，其 中xi为m维特征向量；其中xi∈X⊆Rm，yi∈{-1，+1}，i=1，2，…，n；学习率为η(0 ＜η≤1)；

输出：W，b。

（1）训练集T粒化为GT={(G(x1)，g(y1))，(G(x2)，g(y2))，…，(G(xn)，g(yn))}；

（2）随机初始化权值粒向量W=(w1，w2，…，wm)T和阈值粒子b；

（3）从粒化后的训练集中选取(G(xi)，g(yi)；

（4）如果g(yi)*(W·G(xi)+b)为负粒子，则W=W+η*G(xi)*g(yi)，b=b+η*g(yi)；

（5）转至（3），直至g(yi)*(W·G(xi)+b)为正粒子；

（6）输出权值粒向量W=(w1，w2，…，wm)T和偏置粒子b。

（2）粒感知机分类算法

输入：训练集T={(x1，y1)，(x2，y2)，…，(xn，yn)}，权值粒向量W=(w1，w2，…，wm)T和偏置粒子b，测试样本x；

输出：测试样本x的类别。

（1）测试样本x在训练集中粒为化G(x)；

（2）计算f(G(x))=sign(W·G(x)+b)；

（3）计算粒子的大小q(f(G(x)))，为正则判定为正例类别，为负则判定为负例类别。

4 实验分析

实验数据为UCI 数据集，具体描述如表1 所示。特别说明：Movement_libras 数据集具有15 个标签类别，故在该实验中将标签小于8 的类别设为负类，标签大于等于8 的数据类别设为正类。

表1 数据集描述Table 1 Dataset description

数据集的量纲存在差异，因此采用最大最小值法进行样本归一化，从而保证数据值在［0，1］区间变化。最大最小值归一化公式为

为了测试算法的有效性，首先对粒感知机的收敛性进行分析；其次，将选取线性与非线性的数据集，与传统感知机进行比较，测试粒感知机的非线性性能。最后，本文采用多个传统的机器学习分类器算法，比较其分类精度，分析算法的分类性能。

4.1 粒感知机的收敛性分析

本次实验利用Heart 数据集，测试粒感知机误差率是否收敛。首先，从Heart 数据集随机抽取9/10进行训练集，剩下1/10 的数据用于测试分类效果，迭代次数由1 递增到50，实验结果如图2 所示。然后采样10 次交叉验证法进行测试。迭代次数由1 递增到30，实验结果如图3 所示。图2 中，第1 次迭代误差达到最小，第3 次迭代后误差则趋于稳定。从图3 可知，第2 次迭代误差达到最小值，随后几次迭代小幅波动，迭代到第10 次，误差趋于稳定。从图2 和图3 中可以看出，粒感知机具有快速收敛的特性。因为粒化是整个样本空间进行粒化的，其粒子具备全局的信息，因此收敛迅速，迭代次数很少。

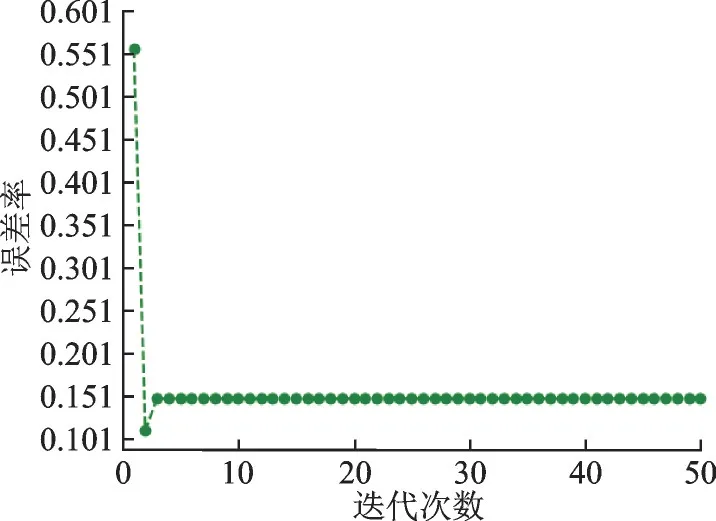
图2 Heart 数据集随机训练的误差率Fig.2 Error rate of random training in Heart dataset

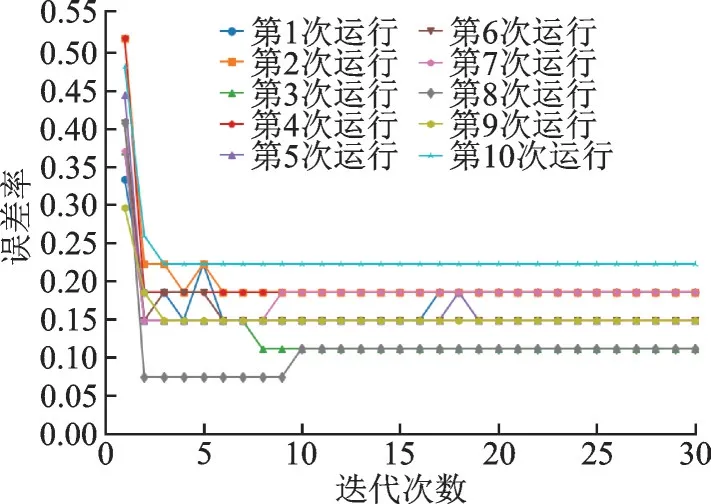
图3 Heart 数据集10 次交叉验证误差率Fig.3 Error rate of ten cross⁃validation of Heart dataset

4.2 粒感知机的非线性性能

众所周知，感知机是一种线性模型，难以表达复杂非线性函数，比如异或XOR。而粒感知机则不同，其参数较多，具备非线性拟合能力。为了验证粒感知机这个优点，本文对XOR 函数进行模拟实验。用决策表表示XOR 函数，如表2 所示。首先本文使用传统的感知机对XOR 函数进行实验。如图4 所示，一些特征的输出与函数的输出值不同，说明传统感知机不具备非线性处理能力。用粒感知机对XOR 函数以及Heart 非线性数据集进行实验。由于本文中的定义采用正例负例的情况，故将XOR 函数的0 值改为-1。实验结果如图5，4 个类型的特征输出均符合XOR 函数；如图6 所示，Heart数据集的准确率也很高，故验证粒感知机具有非线性处理能力。

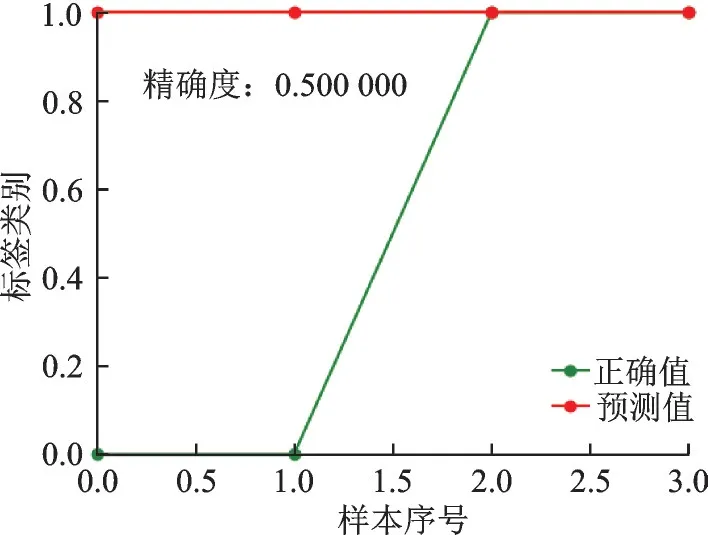
图4 XOR 函数感知机预测曲线Fig.4 Perceptron prediction of XOR function

图5 XOR 函数粒感知机预测曲线Fig.5 Granular perceptron prediction of XOR function

图6 Heart 测试集预测曲线Fig.6 Prediction curve of Heart test set

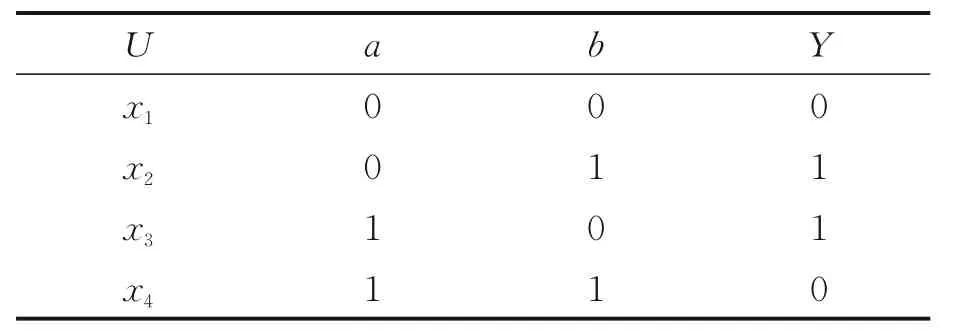
表2 XOR 函数Table 2 XOR function

4.3 分类精度比较

经典的机器学习模型有决策树分类、线性回归、K近邻（K⁃nearest neighbor，KNN）分类、随机森林分类、Adaboost 分类和梯度提升决策树（Gradient boosting decision tree，GBDT）分类。本文采用精确度来评价算法的分类性能。数据集中使用10 次交叉验证取平均值的方法。随机森林分类使用20 个决策树，Adaboost 分类使用50个决策树，GBDT分类使用100个决策树。由上节可知，粒感知机算法在10 次迭代就达到收敛稳定的效果，故这次实验粒感知机使用10 次迭代。如表3 所示，结果保留4 位小数。

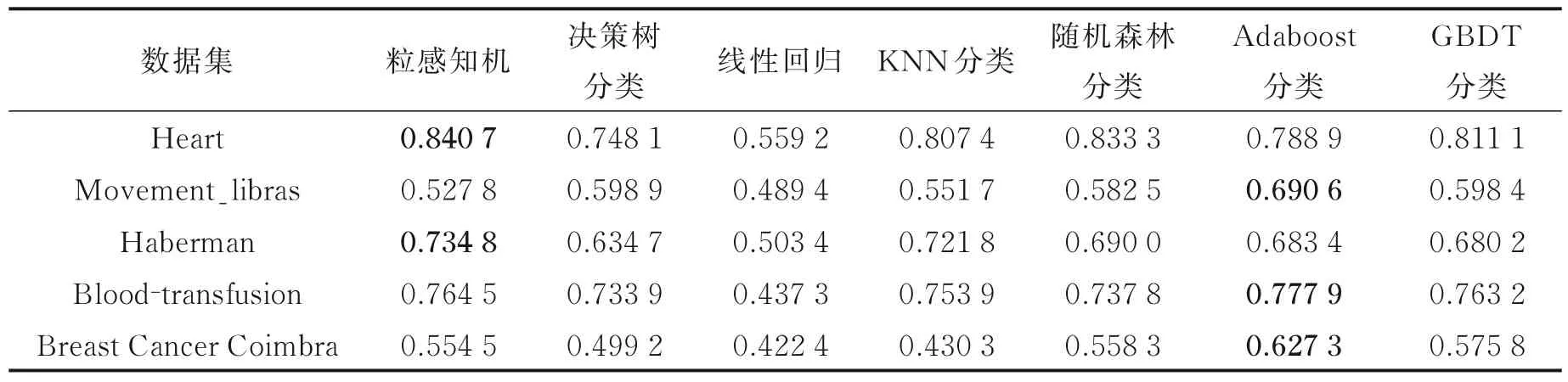
表3 各数据集分类算法精确度比较Table 3 Accuracy comparison of classification algorithms for each dataset

从实验中可以得出，粒感知机算法在Heart 和Haber⁃man 数据集上要明显优于其他算法。除了在Movement_li⁃bras 数据集上精确度弱一些外，在其他数据集上与其他算法相比，大部分情况精确度更高。从这个表中还可以看出，粒感知机算法明显都要高于线性回归的分类精度，由此再次印证了粒感知机算法的非线性分类性能。

5 结束语

传统感知机模型不具备非线性分类性能，故分类效率不高。本文从研究样本的粒化出发，通过定义粒向量的形式，本文提出了一种新型的感知机分类模型：粒感知机。首先，引入特征粒化方法，在数据集系统中构建粒子和粒向量，并定义了粒向量的运算规则。进一步将粒向量进行了应用，设计粒感知机策略，提出了粒感知机学习算法。其次，对粒感知机模型进行参数求解，论证了粒感知机函数的导数形式，得到其梯度下降算法。最后进行实验分析，验证了粒感知机模型的正确性与有效性。在未来的工作中，研究粒的局部粒化方法，提高粒化速度与粒化性能；研究粒的度量方法，提高粒分类器的分类精度。