桥式起重机主梁结构静动态性能研究

谢 飞

（沈阳特种设备检测研究院， 辽宁 沈阳 541004）

0 引言

主梁的重量一般占起重机自重的60%以上， 采用合理的主梁构造形式减轻自重， 其意义不仅在于节约本身所消耗的钢材和降低成本， 同时还因此减轻了厂房建筑结构的受载而节省基建费用。 减轻主梁的自重可以从多方面入手，本课题将就改变主梁腹板的形状，设计新型的金属主梁来达到减轻主梁自重的目的。 本课题所研究通用桥式起重机，额定起重量32t，频繁的启动和制动，在多个环节会产生动力载荷。 本文利用有限元理论，利用ANSYS 有限元分析软件， 对桥式起重机的箱形梁的应力与变形情况进行了分析计算， 同时对桥式起重机主梁进行了有限元模态分析， 得出各阶模态下主梁的固有频率和固有振型，找到主梁振动中的危险区域，并且研究了起升阶段过程中，提起重物和制动时引起的冲击载荷影响。 并且在此基础上，对该起重机原设计提供评价依据，为起重机设计前期提供有效的理论分析和经验总结， 改进设计方法，提高设计质量。

1 桥式起重机主梁有限元模型的建立

本论文以起重量32t、跨度为30.5m 双梁箱型结构桥式起重机为基本模型[2]，实现桥式起重机主梁结构的参数化有限元分析。 课题研究的是对不同规格的系列桥式起重机结构进行参数化建模及有限元分析， 为方便参数化建模，需要对结构进行模型化处理，即简化若干对结构整体强度、刚度影响微小的特征，并使得模型计算结果稍偏于安全。 对于箱形主表梁，主体结构只有一种材料Q235钢，其材料参数见表1。

表1 Q235 参数Tab.1 The parameters of Q235

1.1 单元选择

本文选取SHELL 63 单元，因为它既具有弯曲能力和又具有膜力，可以承受平面内荷载和法向荷载，本单元每个节点具有6 个自由度：沿节点坐标系X、Y、Z 方向的平动和沿节点坐标系X、Y、Z 轴的转动。 应力刚化和大变形能力已经考虑在其中。 在大变形分析（有限转动）中可以采用不变的切向刚度矩阵， 该单元能较为真实的反映主梁结构的实际承载状况。

1.2 网格划分

为使网格划分均匀，对网格尺寸加以控制，此处单元的边界尺寸为100mm。 对生成的模型选择Quad 和Mapped 选项，划分为四边形网格，较大的规则平面均划分为规则形状的网格， 而较小面积处以和受力点处以及加强筋等不规则形状处均划分为自由网格（Smartsize），主梁划分网格后图形见图1， 整个模型划分的单元总数为18239 个，节点数为17755。

图1 主梁划分网格后的整体模型Fig.1 Whole model after meshing of main beams

1.3 加载

桥机的主梁可以简化为简支梁，所以主梁的一端仅释放在垂直平面内的旋转自由度；另一端释放垂直平面内的旋转和沿主梁轴向移动2 个自由度。 作用在起重机主梁结构上的外载荷可以分为固定载荷和活动载荷，其中固定载荷包括由主梁、轨道、走台和栏杆等的重量所产生的均布载荷和由司机操作室、 大车运行机构以及布置在走台上的电器设备等的重量所产生的集中载荷； 活动载荷由小车自重及起吊重物引起的以轮压形式作用在主梁结构上的载荷，并确定动载系数φ1=1.1。 小车位于跨中满载下降制动同时小车启动（或制动），以确定跨中危险截面的最大弯曲应力和最大挠度。

主梁危险工况为小车满载且位于跨中位置时。 在计算主梁强度时（考虑动载影响），小车车轮作用在主梁上的压强为：

2 桥式起重机主梁结构的静态性能分析

由上述分析可知， 以上载荷工况是桥式起重机在工作过程中主梁结构所受到的最恶劣的承载状况， 对其进行强度和刚度分析如下。 p1和p2分别采用面载荷加载在主梁上，实际中载荷作用在轨道上，并对主梁进行加载，应力最大点发生在轮压作用处，产生较大的接触应力，实际工作时是车轮和铺在上盖板上的轨道接触， 会使应力减小，所以此处强度分析符合要求，需要读取主梁跨中局部应力分布规律比较合理。

主梁跨中局部应力分布规律， 最大弯矩发生在小车满载时位于主梁中部下方腹板上， 这一截面几乎处在跨中位置。因此，综合考虑，视跨中截面为最危险截面。应力和位移最大处发生在小车位于主梁跨中时的下腹板处，这里的应力云图见图2， 最大应力节点编号为4601 号节点，最大应力为81.348MPa，Q235 钢许用应力[σs]=177MPa，小于许用应力强度符合要求。

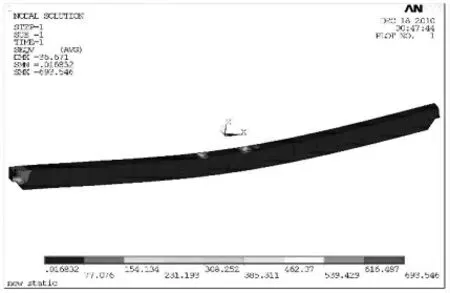
图2 主梁整体受轮压作用等效应力云图Fig.2 Contour plots of the role of the overall effect by the wheel pressure about the main beams

最大位移云图见图3，最大位移值为30.096mm，小于许用垂直挠度43.57mm，刚度符合要求。

图3 主梁等效应力云图Fig.3 Equivalent stress contour of the main beams

3 桥式起重机主梁结构的约束模态求解及分析

利用ANSYS 软件中的Block lanczos 法对桥机主梁的前8 阶模态进行分析[3]，采用两端梁接触（主梁和端梁联接部分）进行约束，见图4。

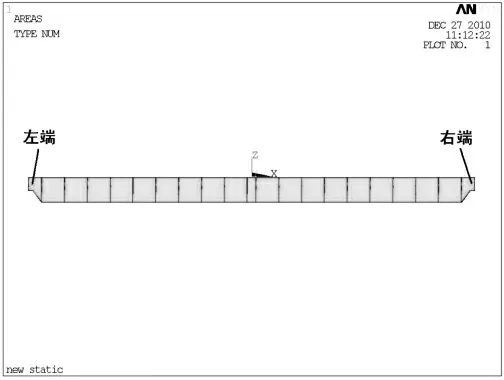
图4 桥式起重机主梁约束示意图Fig.4 Sketch map of the main beam constraints of bridge crane

评价主梁结构动态性能的好坏主要看主梁结构低阶频率。 主梁结构的低阶频率应该高于其他零部件结构的固有频率、电动机的固有频率、减速器及其后续传动系统的转动部件的最高工作频率。对于大型起重机来说，主要是低阶模态起作用，高阶模态可以忽略，前8 阶的阵型模态见图5。

图5 前8 阶模态的位移云图Fig.5 Displacement cloud diagram of the first 8 modes

由以上模态分析的图表可以看出：

通过分析振型，找出结构薄弱之处，判别产生振动的原因。因此，振型分析有利于在主梁结构设计阶段预测其动态特性， 为主梁结构优化和疲劳强度校核提供理论依据。 从振型分析中可知，主梁参与了多种形式的振动，为确保结构预期的疲劳寿命，应在设计和制造中加强上、下盖板与腹板的连接强度，重视该部位焊接质量，以提高其疲劳寿命。

GB3811-1983 规定， 起重机作为振动系统的动态刚度（动刚度），以满载情况下钢丝绳组的下放悬吊长度相当于额定起升高度时系统在直方面的最低阶固有频率（简称为满载自振频率）来表征。对于桥式或门式起重机和装卸桥，小车位于跨中时的自振频率不应不小于2Hz。 从结构的动态特性来看，主梁的第1 阶固有频率为2.81Hz，大于2Hz，符合起重机设计规范。

4 桥式起重机主梁结构的瞬态动力学分析

用有限元法建立桥式起重机动力学模型； 以吊钩处的载荷时程曲线模拟吊重启动、起升和制动工况；通过瞬态动力学分析和谐响应分析， 讨论桥式起重机结构参数和吊重下降速度对主梁跨中的瞬态响应的影响规律；并分析起重机金属结构的稳态频谱特性及随结构参数变化的规律。

本文在模拟起重机动力学问题时，参照其工作，在跨中起吊32t 额定载荷， 研究在提升重物上升阶段这段时间内的情况，时间限定在上升结束时间以前。假定吊钩处的载荷历程如图所示；0.5s 内将吊重从地面完全提起（启动）；0.5s～4s 内匀速起 升；4s～4.2s 冲 击载荷阶段，4.2s～7s内匀速起升，载荷—时间曲线见图6。

图6 单个车轮作用在主梁上的载荷—时间曲线Fig.6 Load-time curve of single wheel load acting on the the main beams

选择主梁跨中危险截面上的Z 方向产生最大位移和等效应力的节点，观察节点的位移-时间曲线，横坐标为时间，单位为s，纵坐标为位移值，单位为mm。可以看出，在加载过程中容易产生冲击，其位移值达尖峰。在全部加载完毕后，上升过程中的制动过程使主梁在产生的冲击载荷作用下，产生了更大的变形。其最大变形值为接近35mm，这个值产生在起吊过程中遇到的冲击载荷处。 与起重机的允许的位移值44mm 相比较小，与此相比较， 在冲击载荷作用下的最大位移值即主梁危险截面产生的最大变形在安全范围内。

观察节点4601 的等效应力-时间曲线，见图8，横坐标为时间，单位为s，纵坐标为等效应力值，单位为MPa。观察曲线可知， 最大等效应力变化发生每个小车车轮在152kN 冲击载荷作用于主梁时， 节点的等效应力值达到了最大接近85MPa，这个应力值比许用应力值要小。 静态计算的同一节点的等效应力值81.348MPa， 可见在冲击载荷作用下， 主梁的等效应力有一定量的增大。 通过以上分析，主梁在承受冲击载荷作用时，刚度和强度满足要求。

图7 节点4601 的位移—时间曲线（mm-s）Fig.7 Displacement-time curve of Node 4601（mm-s）

图8 节点4601 处等效应力—时间曲线（Mpa-s）Fig.8 Stress-time curve of Node 4601（Mpa-s）

5 结论

对桥式起重机主梁原设计中的几点具体结论：

静态计算中，主梁每个车轮作用处，在138kN 载荷作用下，危险截面产生的最大位移为，30.049mm，最大等效应力为52.6MPa，最大主应力为81.348MPa，刚度和强度满足要求。

动态分析过程中， 确定了双主梁结构的8 阶固有模态，一阶模态固有频率为2.81Hz，大于2Hz，符合起重机设计规范，远离工作频率，不会有共振现象产生。

动态分析过程中，冲击载荷作用下，主梁危险截面上位移最大值为接近35mm， 等效应力最大值接近85MPa，比静态数据有所上升，但不超过许用值，刚度和强度满足要求。