导热氧化铝填料配方工艺对界面材料导热性能的影响研究

张岩岩,刘永鹤,李东红,康 乐,王 毅,张 阳

(中铝郑州有色金属研究院有限公司,河南 郑州 450041)

近年来,随着5G和智能化时代的来临及电子设备趋于小型化、集成化,电子设备的发热量成倍增加,这对系统的散热性能提出了更高的要求[1]。导热界面材料是散热系统的关键材料,是连接芯片与散热器之间热量传递的桥梁。然而,用于热界面材料的聚合物,如环氧树脂、硅脂等,具有很低的导热系数(0.1～0.3 W/(m·K)),无法满足快速传热的要求。因此需要开发具有高导热的热界面材料,通常的方法是在聚合物基体中加入导热填料来实现高效的热传导。可以作为导热界面材料的导热填料有:金属氧化物如Al2O3、ZnO、SiO2等;金属氮化物如AlN、BN;碳类材料如石墨烯、石墨、碳纳米管等[3-4]。因为氧化铝来源广泛,价格较低,在聚合物基体中填充量大,具有较高的性价比,因此目前高导热绝缘硅胶材料主要以氧化铝为导热绝缘填料[2]。

目前市场上导热氧化铝填料主要包括致密度较高的高温烧结氧化铝(烧结温度1600～1700 ℃)和高温熔融氧化铝(熔融温度2050 ℃)两大类。高温烧结氧化铝按形貌又分为类球形氧化铝和角形氧化铝,高温熔融氧化铝即球形氧化铝[12]。经试用,这两种产品均不能满足制品(大多为有机硅复合材料-硅橡胶)高导热率的要求。究其原因主要在于作为无机填料的氧化铝在使用时性能较差,主要表现为颗粒填充率低、与有机硅相容性差、体积密度小等。球形氧化铝颗粒为5～50 μm单晶体,颗粒形貌为球状,高填充率、高堆积密度,吸油率低等。但其在高温焰流下氧化铝相变很复杂,由此生产的氧化铝除主要为α相外,往往还含有δ相、θ相等杂相,而这是高热导率要求所不希望的。角形氧化铝颗粒形貌以具有尖锐的棱角为特征,生产成本低,转化率高,但纯度低,填充率低,电导高等导致了其导热材料导热系数低。类球形α-氧化铝相含量高、纯度高、表面光滑,但颗粒形貌为椭圆形,影响填充率,且产品成本较高[5]。基于不同形貌导热氧化铝体系稳定性、高性能、低成本等需求考量,通过实现球形、类球形、尖角形氧化铝填料紧密堆积,搭建导热网络结构,从而提升导热界面材料导热系数,制备出复合导热氧化铝填料复合材料有望得到广泛应用[6],市场需求会越来越大。

颗粒的堆积问题在近百年来一直十分引人瞩目,无论是数学家、物理学家、化学家还是材料科学家[7],研究这一问题的不乏其人,因为这个问题在晶体结构、材料科学和工程技术中都有极为重要的意义。目前,在粉体颗粒填充导热高分子复合材料时为降低孔隙率,增大导热材料的导热性能的研究还未完善,如何提高粉体颗粒的堆积密度、降低孔隙率、提高热界面材料的导热性能是填充型导热高分子复合材料急需解决的问题。为了解决上述问题,本文利用Dinger-Funk 方程进行多尺寸复合氧化铝粉体填料的紧密堆积状态计算研究。

1 材料制备及表征

1.1 原料和试剂

原料:江苏联瑞新材料有限公司的球形氧化铝、中铝郑州有色金属研究院有限公司的类球形和尖角形氧化铝,氧化铝填料形貌见图1。

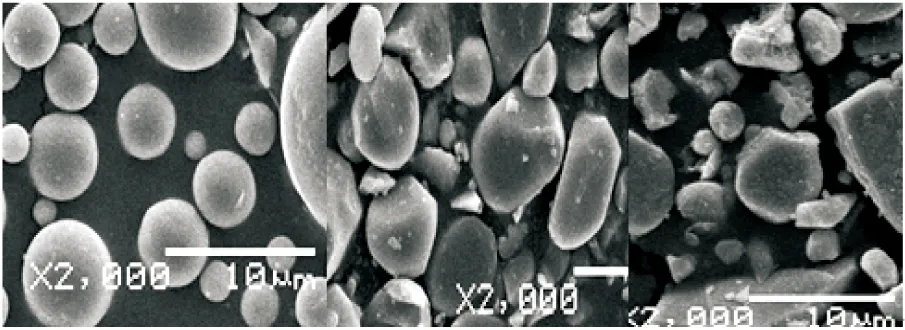
图1 氧化铝填料不同形貌对比图

试剂:广州晨矽新材料有限公司500粘度的乙烯基硅油。实验前进行原料分析和颗粒最紧密堆积理论计算确定氧化铝质量比,粉体性能指标见表1。

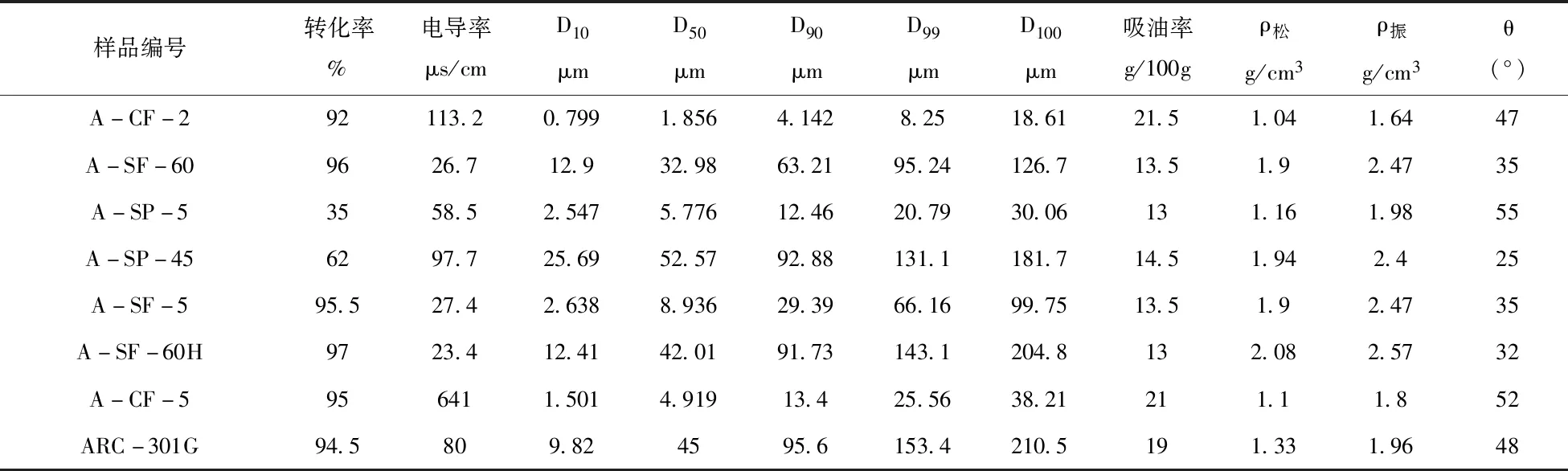
表1 导热氧化铝粉体性能指标

1.2 实验仪器和检测设备

实验仪器和检测设备见表2。

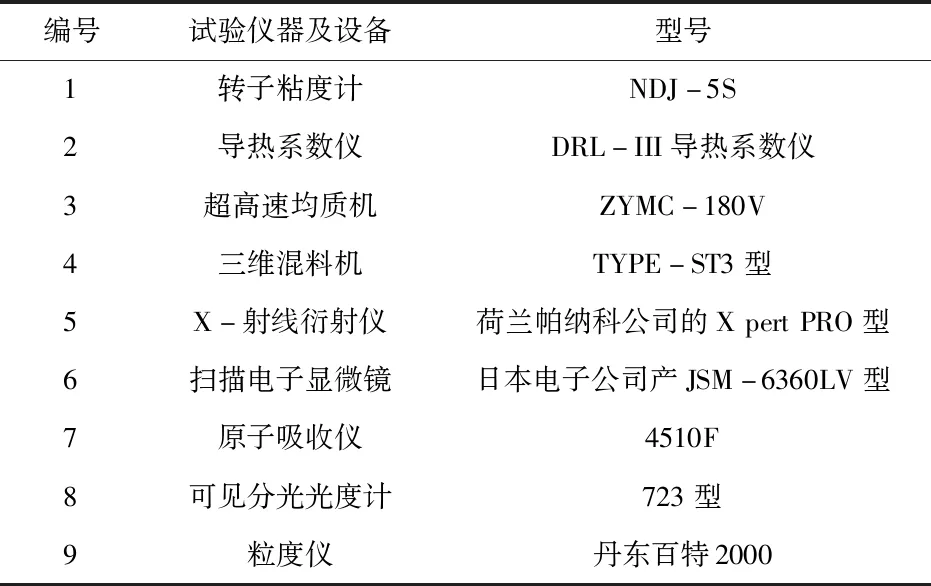
表2 主要试验仪器和检测设备

1.3 试验方法

选取两种或者三种不同形貌的导热氧化铝粉,以Dinger-Funk方程为基础进行最紧密堆积计算,根据计算结果进行复配混料,混合后的粉体按照填充量分别加入一定量的阻凝剂、乙烯基硅油、铂金催化剂和含氢硅油,高速搅拌,硫化成型一定尺寸的导热垫片。具体工艺流程图如图2所示。

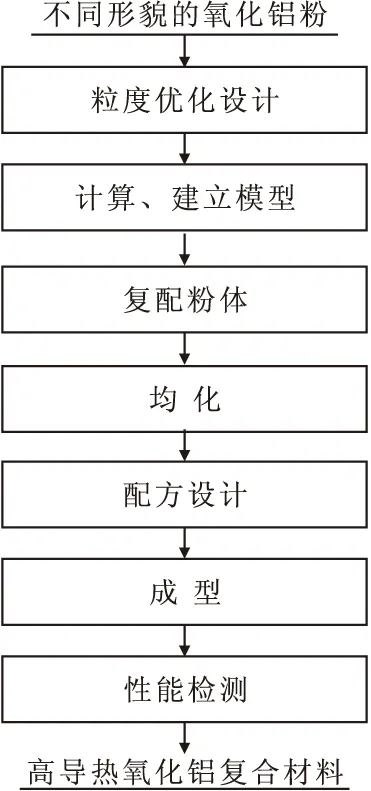
图2 高导热氧化铝复合材料制备工艺图

1.4 紧密堆积计算理论基础

1994 年,Dinger和Funk[8]这位学者对于粒径连续分布且有限小的球形颗粒,提出其颗粒紧密堆积下的累积分布方程:

(1)

式中:D——颗粒粒径,μm;

φ——粒径小于D的颗粒的累积体积分数;

Dmax——体系中最大颗粒的粒径,μm;

Dmin——体系中最小颗粒的粒径,μm;

n——分布模数,最密堆积时的n为0.37。

普遍认为,越接近Dinger-Funk 方程的实际填充体系的累积分布,体系中小粒径颗粒体积与较大粒径的颗粒间形成的孔隙大小越接近,体系的空隙率也越小,体系的填充率将得到很大程度的提升[9]。

但实际不同粒径同一种类的填料体系的累积分布满足方程:

(2)

式中:V——实际体系中填料的总体积,m3;

VD——实际体系中粒径不超过D的填料的体积,m3;

φi——最终体系中第i(i=1,2,…, m, m 为正整数)种原料的体积分数;

φDi——粒径不超过D 的第i种原料的累积体积分数;

φ′——实际体系中粒径小于D 的颗粒的累积体积分数。

结合式(1)、(2)可见,为了实现实际填料体系的紧密堆积, 尽可能使实际的累积分布向Dinger-Funk 方程逼近。在一般情况下,通常采用最小二乘法约束目标函数与实际分布函数, 使φ与φ′之差的平方和最小。所需构建的模型可表达为:

(3)

该数学模型可利用MATLAB 的优化工具箱进行构建,经过编程运算便可得到不同粒径颗粒的最佳体积比φ1,φ2,…,φi,…,φm。

2 结果和讨论

2.1 同等粒径相同添加量,粉体的不同形貌对粘度的影响

选取5 μm和45 μm的球形、类球形、角形氧化铝在添加量75%下测试其对粘度的影响,如图3所示。相同粒径球形氧化铝的粘度最小,角铝粘度最大,相同形貌粒径越大粘度越低。主要是因为同等粒径下,氧化铝球形形貌吸油值最低,角形形貌吸油值最高,而在相同相貌下,粒度越大吸油值越小。

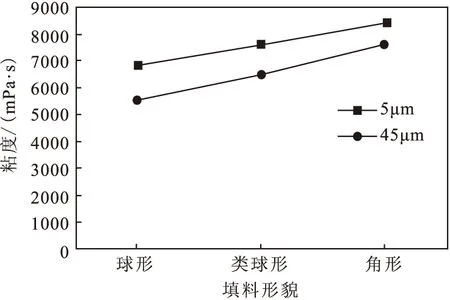
图3 氧化铝填料不同形貌对粘度的影响

2.2 同等粒径不同形貌在不同添加量下对界面材料导热性能的影响

选取45 μm类球形、球形、角形氧化铝,分别在75%、80%、85%添加量下测试对导热系数的影响,如图4所示,在同等添加量下,75%添加量时角形氧化铝导热系数较高。添加量在80%和85%时,类球形氧化铝导热系数较高。在添加量较少时,随着添加量增加三种形貌氧化铝导热系数不断增加。角型氧化铝比表面积大,形成的导热网链会更多,导致导热效果较好[10]。当添加量增加,由于类球形氧化铝是单晶颗粒、转化率高、颗粒表面光滑,导热系数最高,球形氧化铝虽然球形度好但是转化率较低并且颗粒表面粗糙,导致导热系数较低[11]。

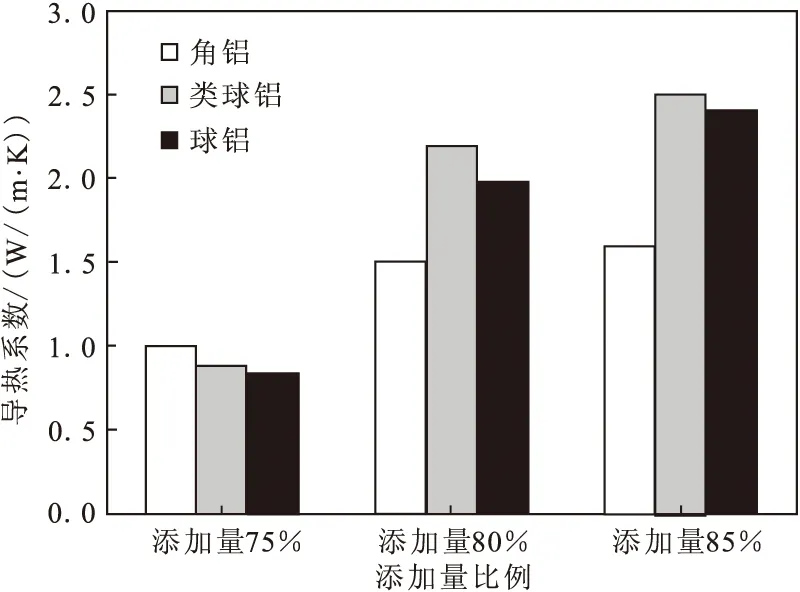
图4 氧化铝填料不同形貌对界面材料导热性能的影响

2.3 同等形貌不同添加量在不同复配比例对界面材料导热性能的影响

考虑最佳性价比和粉体颗粒堆积原理,选取球铝45 μm、类球45 μm和角型5 μm氧化铝以2∶2∶1,2∶1∶1,1∶2∶1,1∶1∶1复配分别在80%、85%、90%的添加量下对导热系数的影响。如图5可见,相同复配比例,随着添加量增加四种复配比例导热系数不断增加,主要是因为添加量增加粉体之间接触点越多,形成导热网络越多,导热系数越大。球铝、类球与角铝比例1∶2∶1时导热最佳,球铝、类球与角铝比例1∶1∶1最差,当复配比例1∶2∶1时颗粒堆积密度最大,形成网络结构最佳,同时类球比例较大提升导热系数更加明显。

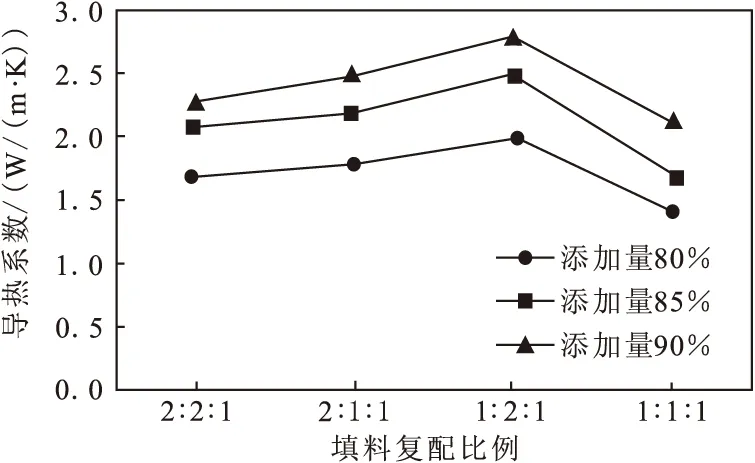
图5 氧化铝填料不同复配比例对界面材料导热性能的影响

2.4 同等添加量及不同复配比例对复配粉体堆积性能的影响

选取球铝45 μm、类球45 μm和角型5 μm氧化铝以2∶2∶1、2∶1∶1、1∶2∶1、1∶1∶1比例复配,对粉体堆积性能的影响。如图6可见,球铝、类球与角铝比例1∶2∶1时堆积密度最大,这是因为颗粒之间缝隙相互填充实现颗粒之间接触点最多,形成导热网络通道越多,从而粉体的堆积密度最大,导热系数最高。

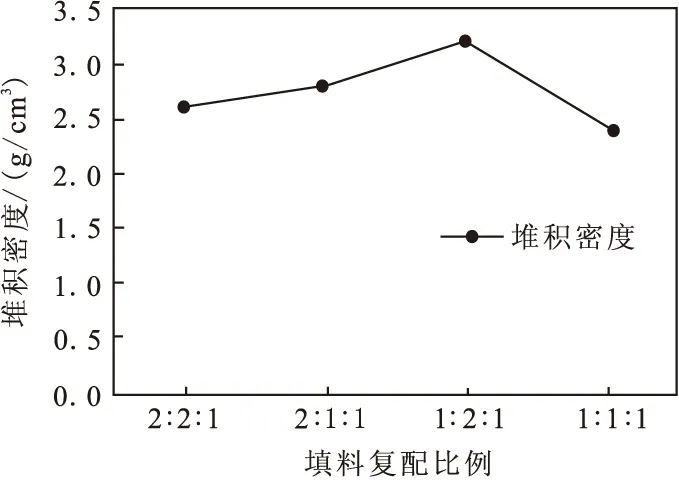
图6 氧化铝填料不同复配比例对复配粉体堆积密度的影响

3 理论计算及样品表征

结合前期试验结果,对较优的配方(A-SP-2、A-CF-5和A-SF-60)进行理论堆积模型计算,图7为三元拟合曲线图,从图7可以看出拟合曲线和理论的紧密堆积曲线无限接近。n=0.37时,理论配方比例为0.088∶0.299∶0.613,其堆积密度为2.69 g/cm3,在92%填充下,制备出复合材料导热垫片的导热系数为3.34 W/(m·K)。通过SEM检测可以看出粉体之间形成紧密的导热网络通道,见图8。

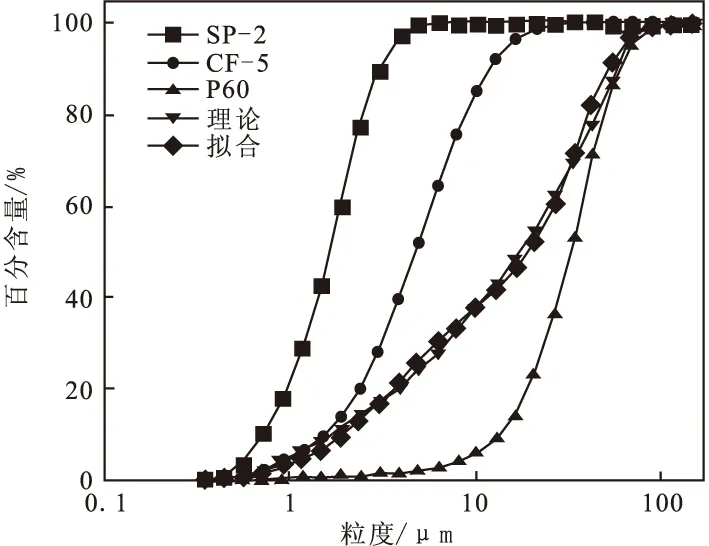
图7 三元拟合曲线图(n=0.37)

图8 最佳氧化铝填料复配粉体SEM

4 结 论

(1)相同粒径和添加量下,球形氧化铝填料粘度最小,角形氧化铝填料粘度最大。相同形貌和添加量下,粒径越大粘度越小;

(2)同等添加量由于类球形氧化铝转化率高、颗粒表面光滑、单晶颗粒大,导热系数最高;

(3)相同复配比例,添加量越大,粉体之间接触点越多,搭建导热网络结构越好,导热系数越大;

(4)球铝、类球与角铝比例在1∶2∶1时堆积密度较大,导热系数较高;

(5)选取A-SP-2、A-CF-5和A-SF-60以0.088∶0.299∶0.613比例复配,通过SEM照片可以看出粉体颗粒之间形成致密的导热网络通道,堆积密度2.69 g/cm3,导热系数可以达到3.34 W/(m·K)。