复合离散型随机变量分布的迭代计算公式

徐 怀

(安徽大学 数学科学学院,安徽 合肥 230039)

风险数学是一个比较热门的研究领域，在各种风险模型中，一般以复合随机变量来刻画索赔过程或收入过程[1-6].复合随机变量概率分布的计算问题理论上可以使用卷积公式完成计算,但这是比较困难的,主要的问题是计算繁琐,精度差[7-8].

本文将以卷积公式为基础,给出一类特殊复合随机变量迭代公式，这个迭代公式的效率和精度大大优于卷积公式,为实际应用奠定了坚实基础.下面首先给出复合随机变量的相关定义.

在风险模型中可以使用复合风险模型刻画一段时间内单张保单或一组保单组的总损失额或总收入额.

定义2假设用来计数的随机变量N的概率分布pn=P(N=n),n≥0,满足下面的关系

可以证明，除退化分布外,此类分布包含且仅包含泊松分布、二项分布、负二项分布，这些分布在精算领域内有着广泛的应用[9-10].

1 迭代公式的证明

为证明的需要，下面介绍两个预备性知识，

证明关于g0的证明是一目了然的，我们略过.

下证gi,i≥1.

分解上式中的第二和第三项得,

分解第一项,分别与第三项和第五项合并得,

分别合并第一和第三项,第二和第四项得,

这是一个效率很高的递推公式,下面将看到它的运用.

特别的若{Xi，i≥1}为取值为正整数,此时f0=0,则可以得到如下的简化公式

2 数值例子

在这一节中，我们以N服从参数为λ的Poisson分布为例，说明上面公式的应用.

由于N服从参数为λ的Poisson分布所以有

比较系数知a=0,b=λ.

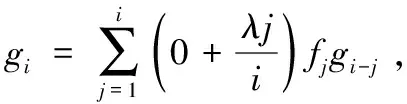
图的分布函数

具体的,若X概率分布律如图1.

X1234567p0.30.200.150.10.050.2

此时f1=0.3,f2=0.2,f3=0,f4=0.15,f5=0.1,f6=0.05,f7=0.2.