聚焦有效对话 构建生长课堂*

林翠霞

德国人克林伯格认为,在所有教学中,都进行着最为广义的“对话”,不管哪一种教学方式占支配地位,相互作用的对话都是优秀教学的一种本质性标志[1]。对话是课堂教学中的基本元素,是课堂教学的基本活动方式之一。基于教材、师生、生生之间的有效对话,能引导学生积极主动地去探明数学知识“是什么”“为什么”和“怎么样”,促进学生的数学思维不断地纵横生长,培育学生的核心素养。基于对话教学理论如何理解有效对话及在课堂教学中的合理运用,本文将从课堂有效对话的内涵、有效对话的价值、有效对话的现状分析、有效对话的教学策略等方面进行一一阐析。

一、课堂有效对话的内涵

所谓有效对话,是指基于学情,立足于以生为本、以学为中心,树立双主体意识,以发展学生长远的数学思维为教学目标,教学过程中教师善于在知识的链接处、本源处、疑难处、易混处、开放处等,以深度问题为引领,在生生互动、师生互动中不断产生思维的碰撞与共鸣,促进学生深层次地理解知识、内化知识、运用知识,培养学生正向的学习意识形态。

二、课堂有效对话的价值

新课程提倡课堂教学中学生独立思考探究与群体交流共享二者兼顾,相辅相成[2]。面对既有差异性的学习群体,在课堂教学过程中实施有效对话,对全面优化课堂教学具有哪些作用呢?

(一) 了解学生学习状态

在教师与学生双向有效对话中,让学生的内心思维可视化,充分暴露学生学习的思维轨迹,教师可以及时了解学生的疑难点、困惑点、易错点或创新点在哪里,为课堂教学调整预设方案提供有力的可靠依据。基于学情的教学跟进,能确保课堂教学过程进展有序,张弛有度,更好地提高教学的针对性与实效性。

(二) 舒展学生独特个性

实施有效对话,改变传统教学的“独白式”或“满堂灌”的教学方式,不禁锢学生的个性思维发展,真正体现学习者是学习的主体。通过教师设计有意义、有层次、有挑战性的话题,引导学生积极思考、主动探究,尽情表达自己的独特想法,展示自己的个性,培养学生善思乐言好问的良好习惯,同时体验自主探究学习所带来的乐趣,增强学生学好数学的自信心。

(三) 建立健康师生关系

教师基于学生立场,选择合适的交流话题,在有效对话过程中,构建宽松温暖的学习环境,让学生内心深处产生愉悦感、安全感、成就感,学生乐于亲近教师,乐于思考,愿意大胆表达自己的所思所想所获,学生的学习主动性不断增强,教师与学生之间关系融洽,从而形成正向循环的教学效应。

(四) 促进学生深度学习

有效的对话教学,能改变学生浅层学习状态。教学中教师抓住数学知识的关键点,调动学生思维,引导学生由浅入深、由表及里、由单一到多维,层层递进地建构知识、内化知识,注重学生求异思维、批判思维的培养,促进学生由浅层思维走向高阶思维,使学生的思维品质得到良好的发展,真正落实学生数学学科素养的培育。

三、课堂教学对话的现状分析

(一) 教师讲解多,学生思考少

多数教师有课程改革的意识,也尝试将教学的主动权还给学生,但在实际教学中,无法做到收放自如,总是担心学生学不懂,总喜欢多讲一些,担心哪些主要知识讲得不够完整,在放手的同时又不知不觉地收手,因而课堂中常常出现教师的单向活动多于学生的个体活动,以部分的精彩代替全班学生的精彩。

(二) 碎片问题多,核心问题少

教学中教师提出的问题较为简单、零散和肤浅,随意性强,所提出的问题不具有思考性,不利于学生思维的发展。较为常见的就是乒乓式的对话,出现伪对话现象。因为教师未能提炼出核心问题,导致一节课下来形离神散,学生的合作交流、自主探究匆匆带过,整体思维处于浅层状态,学生的学习处于被动厌烦的状态,导致教学目标的达成度不高。

(三) 整体划一多,个性发展少

面对大班额不同的学习个体,总存在学生认知储备与思维发展水平的不同,教师未能深入了解学情,摸清学生已有的认知水平。基于学生的个体差异,不能设计有利于全体学生个性发展的对话学习活动,无法有效地落实培优辅差,实现因材施教,难以基于学情分层教学、分层设计问题、关注不同学习层次学生不同的学习需求。

四、课堂有效对话的策略

(一) 在知识的连接处对话

小学数学知识与知识之间是紧密关联的,如果教师善于抓住知识的生长点,在知识的生长点以疑设问,就能有效地刺激学生的思维焦点,激发学生自觉地参与知识的探究之中。教学中教师要深入分析教材,明确所教学的知识在整个学习体系中的前后关联,找准新知教学的切入点,打通新旧知识之间的联系,从而快速地引导学生进入新知的探索旅程。

例如,教学部编版四年级下册“轴对称图形”时,有位教师先出示一些图形,让学生进行辨析,其中的小树图不是轴对称图形,教师提出问题:怎么把小树变成轴对称图形? 然后让学生在方格图上画一画,把自己的想法在方格图上表示出来。展示汇报时,重点让学生说一说变化后的小树为什么是轴对称图形。在学生互动交流中,重点引导学生借助方格图认识轴对称图形的特征:一是对称点到对称轴的距离;二是对称点的连线与对称轴的关系。在学生对这两点特征深入感知后,就可以利用这一特征补全轴对称图形,即先找出图形的关键点,然后确定每一个关键点的对应点,最后连接所有对称点成为轴对称图形。在知识的连接处展开对话,很好地唤醒了学生已有的认知经验,这些已有的经验为学生新知的探究铺好路搭好桥,避免学生探究的盲目性与随意性,提高探究的有效性。

(二) 在知识的疑难处对话

作为教学的组织者和引导者,教师首先要深入地分析学情,对学生的认知困惑了然于胸,再针对学生的认知难点,寻找恰当的途径,在疑难处下功夫,为学生指点迷津拨开迷雾,让学生学会抓住关键,从知识的本质处深刻理解,深层建构,让深度学习在课堂上真正发生。

1.有疑中释疑

例如,教学人教版六年级上册“百分数”问题时,某品牌电脑原来售价3000 元,降价后售价是2600 元,降价了百分之几? 有位教师在教学时组织了与学生如下的对话:

师:降价百分之几是什么意思?

生1:降价后的价格比原来售价少百分之几?

师:把谁看作单位1,谁和单位1 进行比较,少百分之几你是怎么理解的?

生2:降价后的价格比原来售价少的部分占原来售价的百分之几?

师:请画图表示出现价比原价少百分之几,再列式解答。

师:你能对照线段图说一说你的想法吗?

以上例题的问题是简缩式的提问,学生解决这样的问题,弄懂问题的含义是重要前提,学生把问题的含义弄明白了,就可以将这样的问题转化为一步的百分数问题。借助图形与算式融合的方式,引导学生理解数量关系,学生能直观地看到解决降价百分之几,就是求降价后的价格比原来售价少的部分占单位1 的百分之几,学生结合线段图,边比画边讲解,可以很清楚地看到算式的每一部分求的是什么。这样的交流对话,化理性为感性,学生在交流对话中直观地理解知识、内化知识。同时也改变了以往教学中将图形与算式割裂的状态,科学地将图形与算式联系在一起,避免图形与算式两张皮的现象,有效地进行图形与算式之间的语言转换,帮助学生透彻地理解知识。

2.无疑中设疑

教学中,多问几个“为什么”,能撬动学生深层思维的根源。小学阶段学习的五大运算定律主要适用于乘法和加法,较少引导学生思考这五大运算定律与除法、减法的联系。有位教师在教学“运算律的整理和复习”时,提出了这样的问题:为什么加法和乘法有交换律和结合律,而减法和除法没有呢? 除法有没有分配律? 这样的问题一抛出,在学生平静思维水面荡起了涟漪,教师以除法为例,引导学生进行举例验证,发现除法算式都可以转化为乘法算式,如这样可以利用乘法解决问题,就不需要有除法的运算定律。教师的适时追问,引导学生学会用联系的观点思考问题,培养学生思维的独创性。

(三) 在知识的易混处对话

数学知识之间具有关联性与类似性,由于小学生的辨析思维能力较弱,当学完一些具有关联的知识后,在知识运用上容易迷失方向产生混淆。因而教学中教师要有意识地引导学生对具有关联性、类似性的知识进行对比辨析,提升学生的辨析能力,培养学生深刻的辩证思维。

例如,学习稍复杂的分数问题,解决如下两个问题:(1) 农家乐山庄有柿树200 棵,板栗树的棵数比柿树多板栗树有多少棵? (2) 农家乐山庄有板栗树280 棵,板栗树的棵数比柿树多柿树有多少棵? 相当多的学生解决类似这样的问题错误率高,究其原因,主要是学生解题时未能抓住关键句读懂已知量与未知量之间的关联式子。因此在学完分数乘除法问题以后,可以设计一个专项练习,让学生根据关键句发现已知量与未知量之间的关联式子:

根据关键句找出等量关系以后,教师要引导学生对这些式子进行归纳概括,将前两个等量关系用字母表示为后四个等量关系表示为a× (1进一步引导学生思考:当a 是已知数时,表示的是什么? 当a 是未知数时,又表示什么?通过这样的对比梳理,让学生对所学过的六种分数问题加以全面认识,从而明确在什么情况下用乘法计算,在什么情况下用除法或方程解答,抓住关键分析比较,促使学生明晰了解题的道理与思路,学生在思辨中不断地完善知识的整体构建,形成更加完整清晰的认知网络。

(四) 在知识的开放处对话

开放性的问题,能触发学生深层思维之弦,促进学生积极主动地探索,发展学生的发散思维,满足不同学生个体的学习需求。通过展示交流学习个体不同的解决方法,丰富学生的思维方式,增长学生的认知视野,让学生的学习既有深度也有宽度,学生所学知识具有饱满感,促进学生学科核心素养的培育。

例如,教学四年级下册“轴对称图形”时,教师设计了如图1 的题目:下图是一个图形对折后的形状,请你想象它原来的样子,画在方格纸上。要解决这个问题,需要根据轴对称图形的特征,找准关键点并找到对应点,然后依次连接起来。根据图1,学生可以根据找对应点的方向不同,所画出的轴对称图形也不同,呈现了如图2 的5 种不同画法。像这样,充分展示学生的不同解答方法,将一道习题的价值最大化,达成了以点带面、以一见多的教学目标,有效地培养学生的求异思维,发展学生的空间想象。

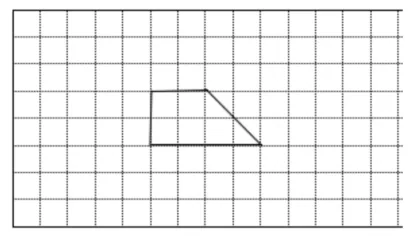
图1

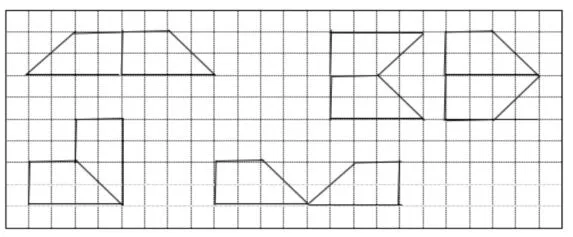
图2

总之,对话不仅是教学的手段和艺术,更是教学的理念和精神[3]。有效的课堂教学对话,创设和谐平等的学习氛围,变“一言谈”为“群言谈”,丰盈了师生之间的内心情感,促使学生想学;触动学生思维深处之弦,促使学生爱学;启迪学生的智慧火花,促使学生会学。有效的课堂教学对话,引导学生深入理解知识本质,学生对知识的建构在知其然的基础上,更知其所以然。