支持我国信息技术课程评价体系构建的计算思维描述框架设计
冯友梅 王珊 王昕怡 周彤彤
[摘 要] 信息技术课程计算思维评价体系的构建需要以系统的评价目标体系为基础,但此评价目标体系很难形成。直接原因为:作为评价目标确定的重要依据,既有计算思维描述框架中“过程”维度的要素不能进行多层粒度细化。深层原因则为:认知心理学对“思维过程”与“思维内容”的人为割裂。鉴于此,为从根本上突破计算思维评价困境,文章以“知识与思维内在统一”为基本立场,将“计算思维过程”与“计算思维内容”还原为完整的动态计算思维,在此基础上寻找与动态计算思维内在一致的静态知识结构。经过层层剥离、转换,最终形成包含“计算概念”与“计算策略”两个维度的计算思维二维描述框架。该描述框架中各维度的要素集合亦是具有信息技术学科本质特征的核心知识集,其不仅可以支持从宏观到微观的多层计算思维评价目标体系以及评价体系的构建,而且可以为信息技术课程“单元群—单元—课”整体教学设计提供必要抓手。
[关键词] 计算思维; 计算策略; 描述框架; 信息技术课程; 评价体系
[中图分类号] G434 [文献标志码] A
[作者简介] 冯友梅(1983—),女,河北香河人。讲师,博士,主要从事信息技术课程与教学、基于清晰图形语义的思维可视化研究。E-mail:youmeifeng2008@163.com。
一、引 言
作为信息技术课程的重要学科核心素养,计算思维的评价问题备受关注。经过上一轮基础教育课程改革的洗礼,发展性评价的理念已深入人心。以促进学生发展为旨归,我国K-12阶段信息技术课程的计算思维评价便不能仅是长时间学习结束后的粗粒度的水平测量,而应是由细粒度的微观评价、中粒度的中观评价以及粗粒度的宏观评价共同构成评价体系。其中,系统设计的细粒度微观评价尤为重要。顯然,此计算思维评价体系在我国尚未形成。事实上,虽然国际范围内对计算思维的评价问题关注已久,且已形成大量评价方案及案例,但评价普遍聚焦宏观层面,与“体系”相距甚远。
众所周知,计算思维描述框架(Computational Thinking Framework)是抽象的计算思维定义与具体评价实践之间的桥梁,是评价设计的重要指导和依据。故本文认为,计算思维评价难成“体系”,极有可能根源于计算思维描述框架。基于此,本文系统梳理既有计算思维描述框架,深入分析其存在的问题及原因,在此基础上构建可支持K-12阶段信息技术课程计算思维评价体系设计的计算思维描述框架。
二、既有计算思维描述框架存在的问题及归因
(一)既有计算思维描述框架梳理
目前国际范围内有较高影响力和认同度的当属博南与雷斯尼克(Karen Brennan & Mitchel Resnick)于2012年提出的计算思维描述框架(下文简称“博南框架”),该框架聚焦编程领域,包含计算概念、计算实践及计算观念三个维度[1]。其中,计算概念指从事编程实践时所涉及的基本概念,包括“序列”“循环”“事件”“并行”“条件”“操作符”“数据”;计算实践指基于计算概念发展的、存在于但不限于编程领域的实践,包括“增量与迭代”“测试与调试”“重用与重组”“抽象与模块化”;计算观念则指在计算实践过程中逐渐形成的对自身、自身与他人的关系以及周遭技术世界的基本观念,包括“表达”“连接”“质疑”[1]。考虑计算概念、计算实践两维度与我国信息技术课程对计算思维的内涵及外延的界定较为契合,故本文仅就这两个维度展开深入探讨①。如果从过程视角审视,那么计算概念便可看作计算思维运转过程中被调动、利用的“资源”,计算实践则指向运转过程本身。正如该框架的设计者所言,“计算实践聚焦思维与学习的过程,它指向学生如何学习,而非学到了什么”[1]。较之计算概念,计算实践显然是计算思维更为核心的构成要素。
与仅面向过程的操作性定义(单维度框架),如“抽象、分解、算法思维、概括和模式化、评价、逻辑思维”[2],“界定问题、抽象特征、建立模型、形成问题解决方案、总结迁移”[3]等相比,博南框架对计算思维进行了更为细致的要素切分,对于实践而言也更具操作性,因此,一经推出便吸引了众多研究者和实践者的关注,近年来国际范围内亦不断出现各种改良版本。例如:钟柏昌等在保持博南框架基本结构(三维结构)不变的前提下,对各维度要素做了细微调整,具体为:在计算概念维度增加了“对象”“指令”两个要素;将计算实践维度的四个要素调整为五个,分别为“规划与设计”“抽象与建模”“模块化与重用”“迭代与优化”“测试与调试”;计算观念维度也从三个要素被调整为四个要素[4]。Grover和Pea 则将三维结构调整为两维结构——计算概念和计算实践,且与博南框架中计算概念维度仅面向编程领域不同,该框架中计算概念面向更广泛的计算实践领域,要素包括“算法和算法思维”“模式和模式识别”“自动化”等;计算实践维度则与博南框架大体一致,包含“问题分解”“测试与调试”“迭代细化”等[5]。
其他改良版本不再一一列举。总体来看,虽然在维度或维度包含的要素等方面存在差异,但博南框架的一个重要特征——各维度的基本指向,却被各改良版本所继承,即在各改良版本中,计算概念均指向计算思维运转过程中被调动、利用的“资源”,计算实践则指向动态运转过程本身。本文将博南框架及其改良版本统称为“博南风格计算思维描述框架”(简称“博南风格框架”)。
(二)博南风格框架的问题分析
国际范围内关于思维的研究由来已久,研究者一般将思维过程(形式)和思维材料(内容)作为思维的两个重要组成部分。其中,思维材料即是知识,思维过程则是对知识的加工、利用或调动过程,包括“分析”“综合”“分类”等,思维水平由思维过程水平和思维材料(知识)水平共同决定[6]。可见,博南风格框架中关于计算概念和计算实践的界定与既有思维研究的观点一致。以其为指导,计算概念维度的评价实质上就是知识评价。知识评价多年来一直是K-12阶段教学评价的主要内容,基本思路为:对作为学科教学内容的知识进行分层,使知识粒度细化至课堂级别,最终形成学段、学期、单元、课堂四个层面的粒度不断细化的知识金字塔结构,此知识分层结构与布鲁姆教育目标分类体系(或修订版)相结合,便可形成不同层面的评价目标体系,进而支持系统评价体系的构建。事实上,计算概念维度已经形成的评价体系,如FACT's Systems of Assessments等[7]便是按照以上思路形成的。而依照该思路之所以可形成系统的、可具体到课堂层面的评价体系,关键在于评价实践者可将计算概念维度粒度较大的要素(知识)进行多层切分细化。
反观计算实践维度,该维度的评价是面向计算思维过程本身的评价。以可操作性为目的,博南风格框架亦将完整的计算思维过程进行初步切分,形成如前文所述的若干要素。同样,为了更有效地指导评价实践,计算实践维度的若干要素又被进一步细化。例如:将“抽象”细化为“删除”“过滤”“提取”“符号化”四个要素,将“分解”细化为“分解”“有序”“递归”三个要素,等等[8]。又如:将“重用与重组”细化为“从新问题或新目标的角度评价既有问题或问题解决方案”“在新的问题情境中重用既有方案”“部分或整体调整既有方案以适应新问题”“在重用、重组、再造之间做评估和权衡”四个要素,等等[9]。然而问题在于,在既有文献或评价实例中,计算实践维度诸要素均只做了如上文所述的一层细化,尚未有如“知识金字塔结构”的、将计算实践维度的要素进行多层细化的“过程金字塔结构”,因此,难以为微观层面的评价提供具体明确的评价目标。
综上,计算思维评价难成体系,实则是计算思维的计算实践维度评价难成体系,其直接原因是此维度的评价目标难成体系。换言之,实践者无法以博南风格框架计算实践维度的要素为依据,形成从宏观到微观的评价目标体系,这是计算实践维度难以形成系统可行的评价体系的重要原因,亦是博南风格框架的问题所在。
(三)博南风格框架的问题归因
事实上,不仅针对计算思维过程,以可教可评为目的,学界对思维过程进行要素切分的尝试由来已久。如前文所述,将思维过程划分为“分析”“综合”“分类”“抽象”“概括”“类比”等要素,但要素粒度始终未能小到如知识粒度般可操作的程度,以至于难以形成有关思维教育的系统可行的目标体系,进而导致其在实践领域至今仍作为知识教育的点缀。此种情况难免让人产生如下疑惑:是否我们的努力方向,即“直接面向思维过程把握思维发展的脉络(评定思维发展的水平)”本身就值得商榷?换句话说,就计算思维过程(计算实践)评价而言,可以尝试采用如下“迂回”策略以突破困境:找到与计算思维过程发展脉络及水平具有实质关联的特定知识(知识结构),通过该知识(知识结构)的发展水平间接推断计算思维过程的发展水平。该“迂回”策略的可操作性表现为以下两个方面:首先,知识粒度可以实现多层细化,进而形成从宏观到微观的目标体系;其次,在实际教学中,我们能朴素地觉察到,如果学生形成了由策略性、概念性、技能性等类型的知识复杂关联而成的知识结构后,便会表现出高水平的计算思维过程。
遗憾的是,以上“迂回”策略被如下论断直接否定:“知识是训练思维的材料,是思维(思维过程)调动、利用的资源。”[10]此论断在教育领域被普遍认同,其言下之意为,思维过程和思维内容(知识)间仅是调用与被调用的关系,二者在发展脉络及水平方面并无内在实质关联。计算实践维度的评价也因此论断再次陷入僵局。
计算思维评价落地的紧迫性促使我们不得不进一步追问:以上论断是否禁得起推敲?众所周知,心理学是教育学的直接理论基础,教育领域的核心论断或观点均与心理学存在渊源关系。经系统追溯分析,“思维过程与思维内容(知识)无内在实质关联”的论断直接承自于认知心理学关于学习核心机制的“信息加工”隐喻。该隐喻认为,学习过程便是信息加工过程,是作为“程序”的“思维”对作为“信息”的“知识”的加工过程,“程序”与被其加工的“信息”间无内在实质关联[11],我们将其称为学习的“过程+内容”模型[12]。然而,让人颇为惊讶的是,作为认知心理学的根基,此信息加工隐喻竟来源于与计算机科学的简单类比[12]。因此,我们便有理由怀疑认知心理学对于学习核心机制的信息加工隐喻的合理性,进而也有可能推翻教育领域关于“思维过程与思维内容(知识)无内在实质关联”的论断,从而为计算思维评价顺利走向实践扫清障碍。
三、支持评价体系构建的计算思维描述框架设计
自2016年至今,笔者及团队成员从核心素养的落地困境入手,层层追溯,最终发现认知心理学关于学习核心机制的“信息加工”隐喻的局限性。在此基础上,从皮亚杰发生认识论(“新理论”)之哲学精髓处获得启发,得到关于思维过程与思维内容間关系的全新认识:思维过程与思维内容是本质上不可分的统一整体(并无独立于思维内容的思维过程),这一整体可表现为两种状态:静态与动态。其中,静态即是知识,是陈述性知识与程序性知识复杂交织的知识结构;动态即是思维,是以既有知识结构为基础的知识结构再建构过程,其结果是新的知识结构的形成,此知识结构又是下一次思维运转的基础,如此螺旋上升,使得知识与思维具有内在一致性,表现为静态的知识结构与动态的思维结构在发展过程与水平方面的同步和统一[13]。
以“知识与思维内在统一”为基本立场,博南风格框架的困境的突破口便不是寻找与计算思维过程(计算实践)内在一致的知识,而是寻找与作为整体(过程与内容的整体)的动态计算思维内在一致的静态知识结构,此知识结构便是系统的计算思维评价目标体系乃至评价体系的构建依据。
(一)从作为“社会需求”的计算思维到作为“教育目标”的计算思维
与计算思维动静交替、内在一致的究竟是什么样的知识?此问题的有效回答始于对计算思维内涵的系统梳理。
计算思维概念于2006年被周以真教授首次正式提出,她认为,计算思维就是“用计算机科学的基础概念解决问题、设计系统及理解人类行为,即像计算机科学家一样思考”[14]。可见,彼时计算思维与“计算机”的关系颇为密切。随着计算思维理论与实践研究的不断深入,计算思维也逐渐从计算机科学领域走向更广泛的实践领域。例如:2014年,周以真教授将计算思维的定义修订为,“计算思维是一种思维过程,包括两个方面,即建构问题模型,以及用人或机器可以有效执行的方式表示问题解决方案”[15],同时,她特别强调,“人们不利用计算机也可以学习计算思维”[15]。再如:我国《普通高中信息技术课标标准(2017版)》中也指出,“利用计算机解决问题的过程与方法(计算思维)可以迁移到其他领域问题解决过程中”[3]。同时,众多面向过程的计算思维操作性定义(如界定问题、抽象特征、建立模型、形成问题解决方案、总结迁移[3])以及颇有影响力的国际计算思维挑战赛(Bebras)的命题取向,均将计算思维泛化为“解决问题的思维过程”。由此难免让人产生如下疑惑:计算思维的边界究竟在哪里?
如果计算思维仅作为社会对教育的需求,作为人们“议论”教育时的谈资,则没有必要深究其边界问题。然而,当下计算思维已经从社会需求转化为教育目标,更具体地转化为信息技术课程的核心目标,那么厘清其边界对于课程建设及教学实践而言均至关重要。所谓厘清边界,即是对如下问题作出审慎回答:当社会向基础教育领域提出“计算思维”的教育需求时,基础教育真正缺失的是什么?亦即,从看似无所不包的计算思维中,提炼、剥离出其真正的教育指向,由此,将作为“社会需求”的计算思维转化为作为“教育目标”的计算思维。
(二)计算思维的教育指向——策略性知识体系
计算思维究竟指向基础教育的何种缺失?笔者认为,既然思维与知识具有内在一致性,且我们的最终目的是寻找作为计算思维的运转基础及与其内在一致的知识,那么以上问题便可进一步转换为:计算思维指向基础教育的何种“知识”缺失?
基础教育的最终目的是赋予学生“能够适应终身发展和社会发展需要的必备品格和关键能力”[16]。其中,必备品格大体对应价值观,关键能力则大体对应世界观和方法论。换句话说,经过基础教育后,学生应在头脑中形成特定的世界观、方法论及价值观体系。反观我国基础阶段的课程设置,首先,科学类课程(如物理、化学、生物、历史等)占比较大,无论是自然科学还是社会科学类课程,其目的均是引导学生从不同角度理解世界,在此基础上形成世界观体系;其次,以语文、政治(道德与法治)等学科为主阵地,其他所有学科为辅,亦能支持学生价值观体系的建构;最后,对于方法论体系,虽然其对学生未来发展的重要性从未被质疑,但在计算思维走进课程标准之前,没有任何课程或课程群支持其系统建构。
这里需要特别强调,方法论具有层次结构,由上到下分别为哲学方法论、一般科学方法论、具体科学方法论。以为学生的未来发展奠基为目的,本文中的“方法论体系”指一般科学方法论体系及其上层的哲学方法论,如“分治”“变治”“减治”“统筹”“迭代”“可视化”等,不包括具体科学方法论。从心理学视角,以上方法论体系又可称为“策略性知识体系”[17]。显然,策略性知识体系对于学生终身发展和未来发展至关重要,但截至目前,该类知识在K-12阶段并未得到足够重视,仅在个别课程中偶有涉及,如语文学科中“曹冲称象”内含变治策略,数学学科中的“数形结合”内含可视化策略,信息技术学科中的“信息系统开发过程”内含分治策略等,其结果便是,学生头脑中仅有零散的策略性知识,远未形成策略性知识体系,以至于在面对复杂问题时缺少系统规划的意识和能力,难以给出高效的问题解决方案。这显然有悖于“核心素养”的初衷。
综上所述,当下接受完基础教育的学生,其知识结构中缺少一类非常重要的知识——策略性知识体系。此类知识体系是学生有效解决复杂问题的必要且重要的基础,其缺失已经导致学生解决复杂问题的能力不足。至此,经过层层分析、剥离和转换,我们最终提炼出计算思维提出者意欲表达、但尚未厘清的教育指向——策略性知识体系。也就是说,解决复杂问题的动态思维过程需要各种类型的静态知识体系作为基础和支撑,其中最为核心的便是策略性知识体系,但这恰是目前学生的短板所在。作为教育目标,计算思维便聚焦于此。
(三)计算思维二维描述框架——计算概念与计算策略
1. 计算思维的知识基础:计算概念和计算策略
承接前文,作为信息技术学科核心素养,计算思维指向策略性知识体系。然而,策略性知识体系并非独立于其他类型的知识,而是作为知识网络的一部分与其他类型的知识复杂交织在一起[18]。因此,策略性知识体系的建构亦需其他类型的知识作为必要支撑。如果我们把信息技术学科的所有学科对象的集合定义为“信息技术世界”,那么从信息技术世界自身的角度,这些处于支撑地位的知识包括有关信息技术世界内部的各种对象及其属性的知识、各类信息系统运行过程及其控制机制的知识;从人与信息技术世界之关系的角度,包括各种实践过程及其目标的知识。策略性知识体系便“鑲嵌”于以上各类知识之中。借鉴博南风格框架的描述方式及概念指向,我们将以上所有处于支撑地位的知识称为“计算概念(Computational Thinking Concepts)”,相应地,将策略性知识体系称为“计算策略(Computational Thinking Strategies)”。这两类知识作为静态知识基础,支持动态计算思维过程的运转,并与其动态统一。由此,便形成了计算思维描述框架的两个维度:计算概念和计算策略。
2. 计算思维描述框架:计算概念及计算策略两维度及其核心要素
显然,作为计算思维的两个维度,计算概念与计算策略均属于知识范畴。依前文所述,知识可以被多层细化和切分,因此,以上两个维度均可形成从宏观到微观的评价目标体系,从而支持系统的、可落地的计算思维评价体系的构建。当然,作为评价的一种方向性指引,计算思维描述框架仅给出以上两个维度的核心要素(顶层要素)即可,无须给出完整的要素金字塔结构。
对于计算概念与计算策略维度核心要素的提取,我们采用自上而下与自下而上相结合的方式进行。
首先,从K-12阶段信息技术学科的上游学科——计算机科学与技术学科中寻找要素提取的线索和依据。事实上,自20世纪90年代起,国际范围内高等教育领域计算机科学与技术学科便开始了对如下问题的追问:“作为一门学科,计算机科学与技术应该让学生了解哪些富有智慧的核心思想?亦即计算机科学与技术学科中具有共同、本质特征的内容是什么。”[19]经过若干年的探索和努力,现已提炼出学科核心概念、核心方法以及核心知识领域。其中,学科核心概念包括“算法”“程序”“硬件”“软件”“效率” “安全性”等;学科核心方法包括“分解”“封装”“模块化”“递归”“迭代”“折衷”“重用”等;学科核心知识领域包括“离散结构”“程序设计基础”“算法和复杂性”“操作系统”“网络计算”“图形学和可视化计算”“信息系统”“软件工程”等[20]。以上计算机科学与技术学科核心方法是信息技术学科计算策略维度核心要素提取的重要依据,核心概念和核心知识领域则是计算概念维度核心要素提取的重要依据。
然后,以计算机科学与技术学科的核心知识领域、核心概念和方法为方向性指引,系统梳理分析国际范围内(以我国为中心,包括英国、美国、澳大利亚、日本等国家)K-12阶段信息技术课程标准、教材及典型课例,从中归纳和提取共有的、具有学科本质特征的内容。在梳理、归纳、提取的过程中,一方面,以上游学科(计算机科学与技术)的研究成果为依据,对既有课标、教材中缺失的(或未显性提出的)、具有学科本质特征的内容做必要提炼和补充;另一方面,以K-12阶段信息技术学科的基本理念和学生特点为依据,将上游学科核心知识领域、核心概念和方法做取舍与调整后向下映射。以上两条路径同时进行,最终汇聚形成计算概念维度和计算策略维度的核心要素集合。
计算策略维度共包含13个核心要素,分别为“分治”“减治”“变治”“封装”“重用”“可视化”“迭代”“统筹”“折衷”“贪心”“蛮干”“回溯”“动态规划”。显然,一方面,以上计算策略均可在信息技术学科找到实例,如“信息系统自顶向下的开发过程”“递归算法”“网络体系结构”等都内含分治策略,“折半查找算法”“快速排序算法”等内含减治策略,“蒙特卡洛算法”内含变治策略;另一方面,这些计算策略对于学生发展而言又有超越信息技术学科的更为基础的意义和价值。也就是说,以信息技术学科知识(计算概念)为支撑,此策略性知识体系(知识结构)一旦在学生头脑中形成,便可向其他学科及生活领域迁移,从而表现出高水平的计算思维过程。
依前文所述,计算概念是计算策略的支撑,剥离出策略性知识后,剩余的所有信息技术学科知识均归属于计算概念范畴。因计算概念维度包含的知识类型较多,为有效指导评价实践,我们将此维度进一步细分为三个子维度,分别为:“对象与属性”“过程与控制”“目标与实践”。其中,“对象与属性”及“过程与控制”子维度是从信息技术世界自身角度提炼的结果,“目标与实践”子维度则是从人与信息技术世界关系的角度提炼的结果。同时,“对象与属性”维度的四个核心要素——“信息技术工具”“数据”“算法”“信息系统”又分别指向信息技术学科的四个核心知识领域。
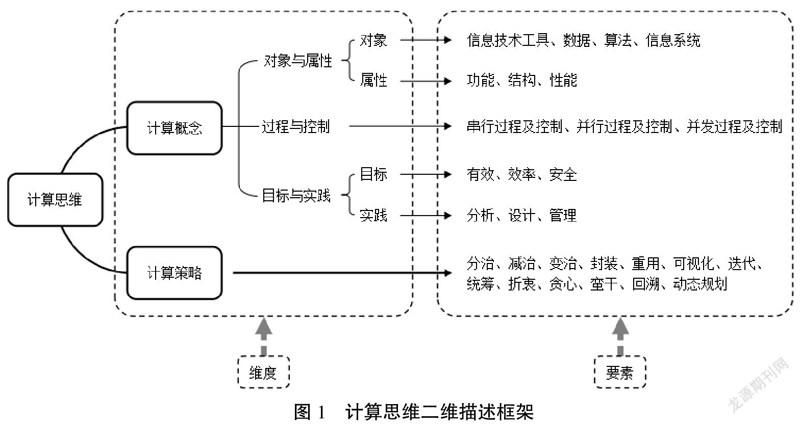
至此,我们完整给出了计算策略及计算概念维度的所有核心要素,以上两个维度(包括子维度)及其核心要素统称为“计算思维二维描述框架”,如图1所示。该描述框架是对我国信息技术课程标准的进一步凝练,描述框架中的所有要素均与课程标准中的特定内容相呼应。因此,本文给出的“计算思维二维描述框架”可以作为既有信息技术课程标准和教材的有效辅助,共同支持计算思维评价的稳妥落地。
四、结 语
本文从我国信息技术课程计算思维的评价困境出发,经过层层追溯、归因、剥离、转换等逻辑过程,最终形成包含“计算概念”和“计算策略”两个维度的计算思维二维描述框架。该描述框架可支持信息技术课程计算思维评价目标体系的构建,进而使计算思维评价真正落地。因篇幅所限,本文未给出基于该描述框架的评价体系设计思路及实例,这些问题将在另文详解。
多年来,信息技術课程存在的必要性和不可替代性一直饱受质疑,本文给出的计算思维二维描述框架正是对以上质疑的有力回应。该描述框架中的所有要素均是具有学科本质特征的核心知识,其计算策略维度的诸要素更是具有对学生发展而言至关重要的、不能被其他学科所替代的价值,这便是信息技术课程的立足之本。期待有更多关注信息技术学科发展的同行能够对本计算思维二维描述框架提出宝贵意见,并携手通过对核心知识的细化和丰富以形成学科稳定的知识体系,在此基础上进一步形成信息技术学科特有的教学、评价方法论及方法体系,使一路艰难前行的信息技术课程真正站稳脚跟,释放其对于学生终身发展和社会发展而言独特的、不可替代的支持力量。
[参考文献]
[1] BRENAN K, RESNICK M. New frameworks for studying and assessing the development of computational thinking [C]//Proceedings of the 2012 Annual Meeting of the American Educational Research Association. Canada: Vancouver, 2012:1-25.
[2] BELL T, HENDERSON T, ROBERTS J. Computational thinking and CS Unplugged[EB/OL]. [2022-01-01]. https://csunplugged.org/en/computational-thinking.
[3] 中华人民共和国教育部.普通高中信息技术课程标准(2017年版)[M].北京:人民教育出版社,2018.
[4] ZHONG B, WANG Q, CHEN J, et al. An exploration of three-dimensional integrated assessment for computational thinking[J]. Journal of educational computing research, 2016(4): 562-590.
[5] GROVER S, PEA R. Computational thinking: a competency whose time has come[J]. Computer science education, 2017(12):19-38.
[6] 林崇德.我的心理学观——聚焦思维结构的智力理论[M].北京:商务印书馆,2008:166-168.
[7] GROVER S, COOPER S, PEA R. Assessing computational learning in K-12[C]//Proceedings of the 2014 Conference on Innovation & Technology in Computer Science Education. New York: ACM, 2014: 57-62.
[8] 陈兴冶,马颖莹.本土化计算思维评价指标体系的构建与探索——基于1410名高中生的样本分析与验证[J].远程教育杂志,2020 (5):70-80.
[9] BASU S, RUTSTEIN D, XU Y, et al. A principled approach to designing a computational thinking practices assessment for early grades[C]//Proceedings of the 51st ACM Technical Symposium on Computer Science Education. New York: ACM, 2020: 912-918.
[10] DEDE C. Technological supports for acquiring 21st century skills[J]. International encyclopedia of education, 2010(3): 158-166.
[11] 安德森.认知心理学及其启示[M].7版.秦裕林,程瑶,周海燕,徐玥,译.北京:人民邮电出版社,2012.
[12] 冯友梅.支持素养教育的教育目标描述模型设计研究[D].南京:南京师范大学,2019.
[13] 馮友梅,颜士刚,李艺.从知识到素养:聚焦知识的整体人培养何以可能[J].电化教育研究,2021(2):5-10.
[14] WING J M. Computational thinking[J]. Communications of the ACM, 2006(3): 33-35.
[15] WING J M. Computational thinking benefits society[EB/OL]. (2014-01-10)[2022-01-02]. http://socialissues.cs.toronto.edu.
[16] 核心素养研究课题组.中国学生发展核心素养[J].中国教育学刊,2016(10):1-3.
[17] 安德森.布卢姆教育目标分类学:分类学视野下的学与教及其测评(修订版)[M].蒋小平,张琴美,罗晶晶,译.北京:外语教学与研究出版社,2009:43.
[18] 丁家永.知识的本质新论——一种认知心理学的观点[J].南京师大学报(社会科学版),1998(2):67-70.
[19] 董荣胜,古天龙.计算机科学与技术方法论[M].北京:人民邮电出版社,2002:1-2.
[20] 董荣胜.计算机科学导论——思想与方法[M].3版.北京:高等教育出版社,2015:32-95.

