工业污水管内流动换热试验研究

王华亮， 曹琳， 方啸岳

（南京理工大学能源与动力工程学院，南京 210094）

0 引言

在某些工业生产过程中，由于生产工艺的原因，会伴随产生大量的30～70℃的废水，这些低温废水中蕴含大量的低品位热能［1-6］。所以工业污水余热作为一种清洁能源已经逐步得到了广泛的认识。目前对于污水源热泵系统，无论是直接式系统还是间接式系统，污水换热方式应用最为广泛的是在换热管内流动换热。而目前污水源热泵系统设计中污水物性参数取值主要是基于清水的物性参数采用倍数法、估算法来确定，取值随意、不科学［7-10］。研究表明在污水各种水质参数中，污水密度、定压比热容、黏度等基础物性参数随着污染物成分不同而存在差异，并且在污水换热研究领域，上述几类物性参数对污水管内换热特性影响较大，从而导致在进行污水换热工程优化设计和换热特性研究时，相关特性参数无法进行科学取值。尤其在工业污水换热研究领域，由于工业污水具有特殊而复杂的成分特性［11-13］，目前在该方向上的研究较少。所以结合实际工程应用中工业污水工况条件，揭示工业污水管内流动换热规律并提出相应的准则关联式，对工业污水源热泵系统的工程设计提供参考具有重要的意义。

1 试验样品

工业原生污水矿化度较高，通常在2000～6000mg/L之间，采油污水主要成分为地层水，而地层水中含有Na+、K+、Ca2+、Mg2+等形成的大量金属盐类［14，15］。参照我国推荐某工业领域污水水质要求主要控制指标SY/T 5329-2012《碎屑岩油藏注水水质推荐指标》和废水中主要污染物成分，配制出6000mg/L的模拟工业污水用于试验见表1。

表1 模拟污水样品成分

参考实际运行工况污水的主要温度范围［16，17］，分别在55、60、65、70、75℃工况下测定污水的基础物性参数，为后续试验开展提供物性参数基础。文中分别采用浮力法、NDJ-9S粘度测定仪［18～20］、水当量法［21］、测定了工业污水在55、60、65、70、75℃温度下的密度ρ、动力粘度μ以及55～75℃区间平均定压比热cp。并依据液体导热系数经验式［22］计算出不同温度下模拟工业水的导热系数，具体测定结果见表2。

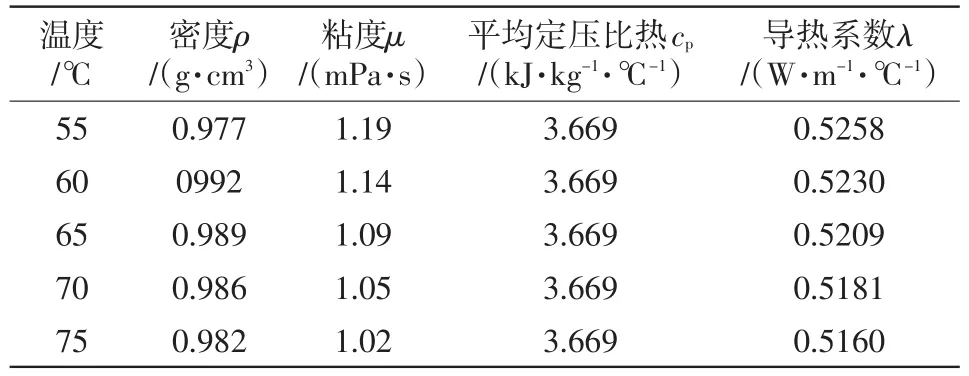
表2 污水样品物性参数

2 试验系统

工业污水的管内换热特性试验系统主要围绕上述试验原理中所需被监测的相关参数进行设计和搭建，试验系统的原理图如图1所示。该试验系统由3个子系统组成：污水循环系统、冷却水循环系统、试验台测控系统。主要包括污水水箱、冷却水箱、循环泵、换热器、循环水管及管件、测控组件等。其中，为了探究工业污水在紫铜换热换热器中的换热特性以及换热准则关联式，试验搭建了污水流动换热试验台，其中为了模拟满液式换热器工况，在换热器中设定污水走管程、冷却水走壳程。

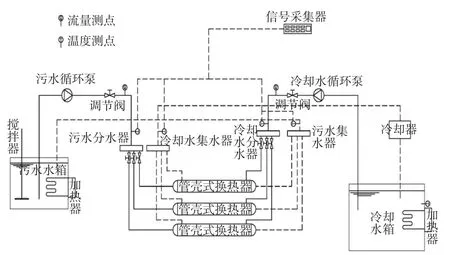
图1 试验台系统

试验中参数监测点主要包括4个温度测点和2个流量测点：换热器污水的进出口温度、冷却水进出口温度、污水流量和冷却水流量。其中污水水箱和冷却水箱中水体的温度通过水箱加热器自带的温度控制器进行监控。采用PT100铠装热电阻对污水和冷却水在换热管段中进出口温度进行信号采集，并将信号传输至MIK-R6000C无纸记录仪进行实时记录和储存用于数据处理结果阶段污垢热阻和传热系数的计算。污水和冷却水在循环管中的流量通过K24高精度化学水专用电子液体涡轮流量计进行实时监测，并通过阀门和流量计的配合调节来实现污水和冷却水流速的调节。

3 试验系统验证

为了保证试验台的可行性，在进行主体试验之前先采用清水试验法对试验台进行热平衡性和可靠性验证。

3.1 热平衡验证

启动清水循环进行试验，待试验系统流量、温度稳定后，采集试验管段的进出水温度和流量，依据能量平衡原理，试验管段管程流体传给壳程流体的热量应该等于试验管段壳程流体的得热量，试验管段的热损失系数η可通过下式计算：

式中，QG为试验管段管程流体传给壳程流体的热量；QK为试验管段壳程流体的得热量。

3.2 可靠性验证

将热流体和冷却流体均先以清水为介质进行清水工况试验。在运行工况稳定后，采集试验数据，通过式（2）计算出在试验管段内污水的对流换热系数h′in，并与相同工况条件下Dittus-Boelter式（3）计算理论对流换热系数进行对比，计算其相对误差。在进行可靠性试试验时，假设换热表面温度均匀、运行过程中流量稳定，整个换热过程换热流体的基本物性不变。

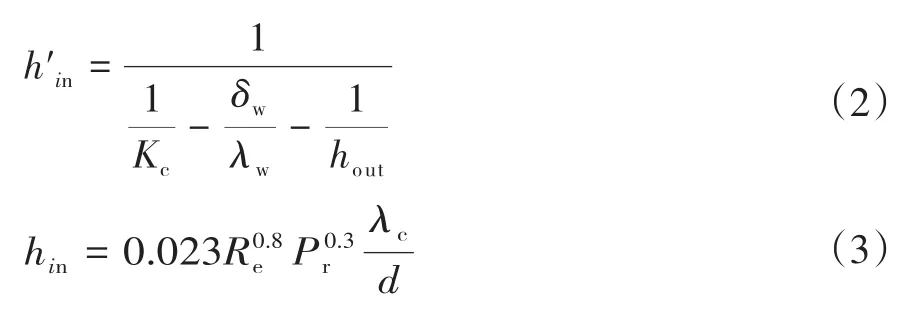
式中，Kc为未结垢时换热管总传热系数；δw为换热管壁厚度；λw为换热管壁导热系数；hout为壳程流体对流换热系数；Re为换热过程流体雷诺数；Pr为换热过程流体普朗特数；λc为换热流体的导热系数；d为换热管特征长度。

在运行工况稳定后，采集60min的清水试验数据通过以上方法得到试验台热平衡性和可靠性测试结果分别见图2和图3。由图2可以看出，在试验工况运行稳定后，换热器管程的散热量基本稳定在4350W左右，而壳程的的热量基本稳定在4200W左右，换热管段的热损失系数基本在1%～5%范围内浮动，其中最大热损失系数为5%，平均热损失系数为3%。由图3可以看出，在试验工况运行稳定后，换热管内实测对流换热系数基本稳定在3000W/（m2·℃），而在相同工况条件下采用经验公式计算的管内理论流换热系数为2920W/（m2·℃），两者的相对误差基本在-3%～7%范围内波动，其中最大极限误差为7%，平均相对误差约为4%。综上所述，试验台的热平衡性和可靠性均满足试验测试要求。

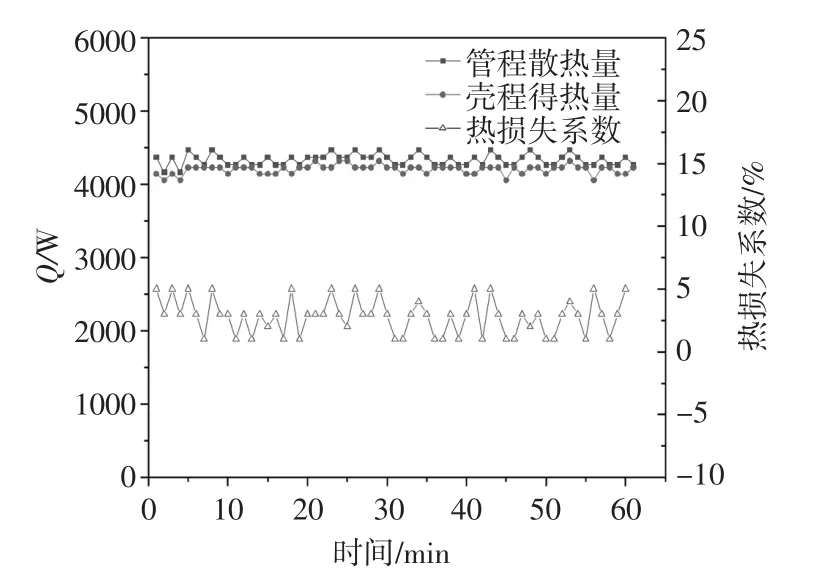
图2 热平衡性测试结果

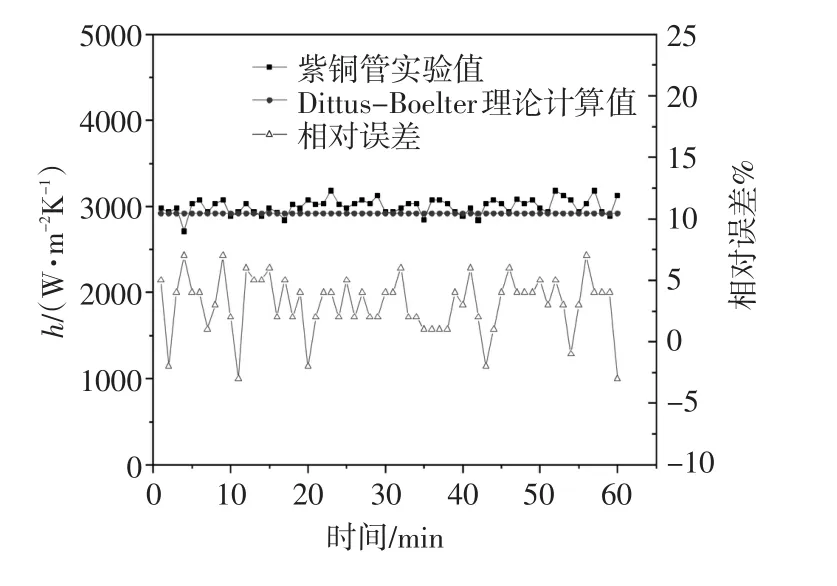
图3 可靠性测试结果

4 数据处理与结果分析

在换热管内还未结垢时，即污垢热阻Rf=0，管内对流换热系数试验值根据试验数据由式2计算得出。其中，总传热系数K根据式4得出，壳程对流换热系数hout根据Zhukauskas经验式5进行修正计算：

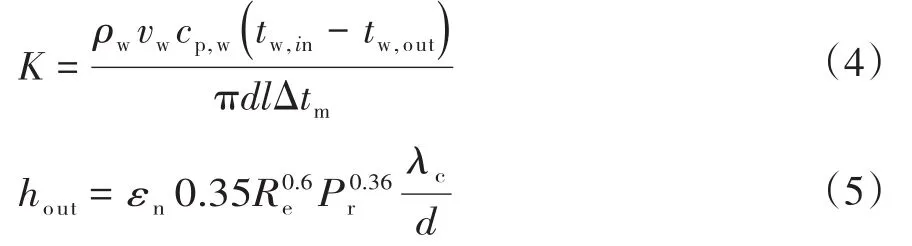
式中，cp，w为污水的定压比热；tw，in为换热管进口污水温度；tw，out为换热管出口污水温度；d为换热管段管径；l为换热管段长度；εn为管排修正系数，取0.84；λc为换热流体的导热系数；d为换热管特征长度，Δtm为换热管段对数换热平均温差。

式中，雷诺数Re、普朗特数Pr以及努谢尔数Nu按照式（6）～式（8）计算：

在工程设计中，努谢尔数Nu、雷诺数Re、普朗特数Pr换热准则关联式常用以下形式进行表达［23］：

式中，ρc为换热流体的密度；u为换热流体流速；μc为换热流体动力粘度系数；cp为换热流体的定压比热，取温度区间的平均定压比热；λc为换热流体的导热系数；特征长度d为对应试验管段管内径，特征温度为试验管段流体的平均温度。

试验过程中调节流量大致在12～26L/min内运行，使得换热管进口雷诺数在3000＜Re＜7000范围内变化，等待工况稳定后采集数据进行处理和分析。3种换热管污水流动换热的计算结果见表3。将试验中式（6）～式（8）所得努谢尔数Nu、雷诺数Re、普朗特数Pr通过最小二乘法进行拟合，得到模拟工业污水在紫铜换热管内换热准则关联式10，拟合优度为92.18%，3000＜Re＜7000。

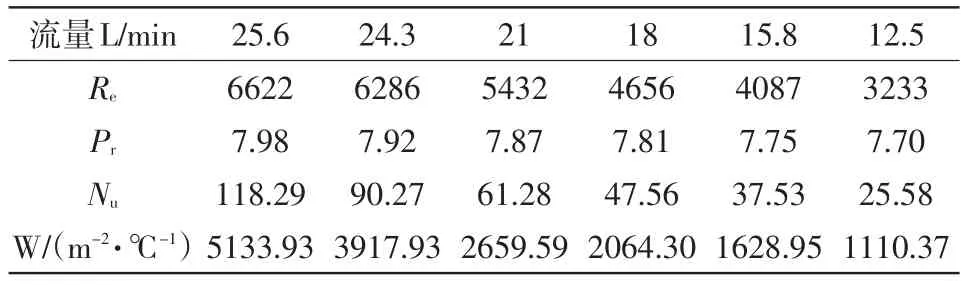
表3 紫铜管换热器试验结果

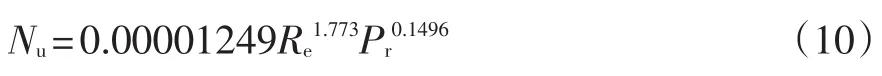
其中，在3000＜Re＜7000试验工况范围内，污水在紫铜管换热器中流动换热时，管内对流换热系数随雷诺数的变化关系以及努谢尔数随着雷诺数、普朗特数的变化规律见图4、图5。

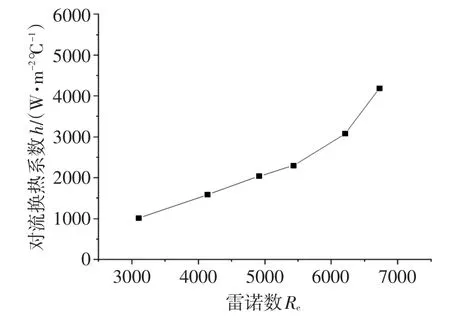
图4 污水管内随Re的变化趋势

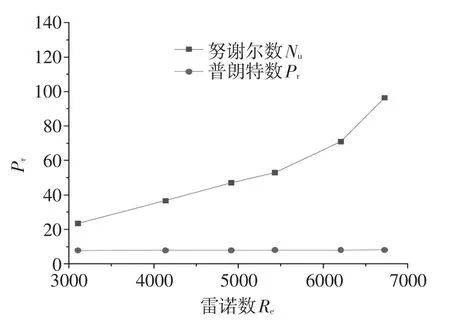
图5 污水管内流动Pr、Re与Nu的变化关系

从图4可以看出，污水在在3种换热管中流动换热时，在3000＜Re＜7000范围内，污水管内对流换热系数随着雷诺数Re的增大而增大。其中，在3000＜Re＜5500范围内污水管内湍流并未达到剧烈状态，对流换热系数的变化趋势要比在5000＜Re＜7000范围内缓慢一些。总体而言，在3000＜Re＜7000范围内，随着Re的增大，管内污水的湍流愈加剧烈，管内对流换热系数变化愈加剧烈。

图5反映出了污水在三种换热管中流动换热时，在 3000＜Re＜7000 工况范围内，Nu随 Pr和 Re的变化关系。从图中可以看出在3000＜Re＜5500范围内，污水的湍流并未达到剧烈状态，对应的Nu变化趋势要比在5000＜Re＜7000范围内缓慢一些。这一现象与管内对流换热系数随Re的变化趋势也相互对应。此外，普朗特数Pr在试验过程中变化较小，是因为在式7中指出，试验中普朗特数Pr与污水的导热系数、定压比热、动力粘度有关，而在试验工况条件下污水的导热系数、定压比热不变、而动力粘度随温度变化很小，从而导致普朗特数Pr变化很小。综上所述，污水在紫铜管换热器管内流动换热时，进口雷诺数Re对管内对流换热系数以及努谢尔数Nu的影响权重要远大于普朗特数Pr，可以通过提高进口雷诺数来提高污水换热器换热效率。

5 结语

文中基于搭建的污水流动换热试验台，在3000＜Re＜7000工况范围内，对6000（mg·L-1）的模拟工业污水进行流动换热试验，结论如下：

（1）经过验证，所搭建的污水流动换热试验台平均热损失系数为3%，最大热损失系数为5%，测试平均相对误差约为4%，最大极限误差为7%。

（2）在3000＜Re＜7000范围内，工业污水在紫铜换热管中流动换热准则关联式为。

（3）在3000＜Re＜7000范围内，进口雷诺数Re对污水管内对流换热系数以及努谢尔数Nu的影响权重要远大于普朗特数Pr。

（4）在3000＜Re＜7000范围内，工业污水在紫铜管内的对流换热系数随着雷诺数Re的增大而增大，可以通过提高进口雷诺数Re来提高工业污水换热器换热效率。