基于双K准则的混凝土断裂力学研究进展

张瑶 ， 刘凯亮 ， 康洪震

（1.唐山学院土木工程学院，河北 唐山 063000；2.河北省建筑工程与尾矿综合利用重点实验室，河北 唐山 063000；3.华北理工大学建筑工程学院，河北 唐山 063000）

0 引言

混凝土作为一种广泛使用的建筑材料，其在复杂环境和复杂结构中的应用日趋增多，迫切需要深入认知其基本性能和破坏机理［1］。作为由水泥、砂，石和水等复合而成的材料，必然存在众多的结合面，这些结合面受到温度湿度变化、收缩、膨胀等因素的影响形成了微裂纹，微裂缝的存在与扩展影响结构的正常使用，重则危及整个结构的安全。

开裂及裂缝稳定性问题一直是混凝土结构的热点问题，断裂力学是专门研究有裂纹物体的强度和裂纹扩展规律的学科，在材料选择，工艺设计等方面发挥着越来越重要的作用，已成为结构设计的重要工具之一。

中外众多学者基于断裂力学开展了对混凝土的研究，建立了多种适用于混凝土的非线性断裂模型，我国学者徐世烺提出的双K断裂模型得到了广泛的关注与肯定。以双K准则为基础和依据，我国第一部混凝土断裂试验规程在2005年正式出版。知名的国际学术组织RILEM在2011年成立了双K断裂准则标准试验方法技术委员会，并邀请徐世烺教授担任主席，充分展现了该断裂准则在国际上所获得的认可。近年来，随着国内外学者的深入探索，双K准则实现了进一步的发展与成熟，并得到了学术界与工程界的共同认可。

文中从试件形式、确定方法、影响因素、延伸准则、理论应用5个方面对双K准则的研究现状进行综述，分析现有成果中仍需深入讨论的问题，展望双K准则的研究前景。

1 双K准则的产生背景

1961年Kaplan［2］率先在混凝土的研究中引入了断裂力学的概念，此后各国学者从多种角度出发，提出基于混凝土材料特点的新假设、新理论、新方法。完成了大量的理论研究与断裂试验，使混凝土断裂力学得以形成，对探索混凝土开裂的条件和规律，有效评判和分析混凝土自身的起裂和断裂性能问题具有十分重要的意义。早期的研究中，人们常采用线弹性断裂理论测定混凝土的断裂参数，然而大量的试验数据反映出明显的尺寸效应，并不是人们所期望的稳定常数，也就难以可靠评估混凝土构件的安全性。随着试验技术的发展，人们发现尺寸效应产生的原因是混凝土裂缝尖端存在的断裂过程区，它是混凝土材料的固有属性，形成机理十分复杂，因此，有效的描述断裂过程区的影响是建立混凝土断裂模型的关键。基于混凝土非线性断裂的特点，研究学者相继提出了一些适用于混凝土的断裂模型，包括虚拟裂缝模型［3］、钝裂缝带模型［4］，及以应力强度因子为参量的两参数模型［5］与等效裂缝模型［6］。其中虚拟裂缝模型和钝裂缝带模型适用于有限元分析，缺乏解析解；两参数模型和等效裂缝模型的测设技术复杂，应用受限。综合上述模型的优点，我国学者徐世烺与 Reinhardt［7，8］提出了双 K断裂模型，该模型引入了起裂断裂韧度和失稳断裂韧度两个参数定量地描述了混凝土裂缝扩展的全过程：

双K断裂准则结合了反映混凝土软化特性的虚拟裂缝概念与缝尖应力强度因子，很好地诠释了混凝土断裂行为机理。

2 双K准则的研究现状

2.1 试件形式

断裂力学试验是研究双K准则的有力手段，其结果直观、可靠。现有的试件形式有：

（1）三点弯曲梁试件，加载方式如图1所示，是应用最为广泛断裂试验试件，由此试件形式所获取的研究成果最为丰富。

（2）紧凑拉伸试件，加载方式如图2所示，通过在对称位置预制孔洞并施加等值反向的力实现加载。

（3）楔入劈拉试件，试件形式如图3所示，加载时的水平劈拉荷载由竖向荷载经楔形架转换而来。

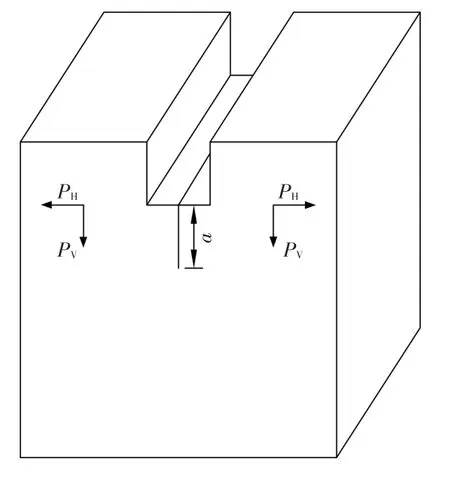
图3 楔入劈拉试件

（4）以上三种属于相对传统的试件，近些年来，一些学者选择了新的试件形式。其中，胡晓威和Ince等［9，10］尝试采用劈拉试验的方法，将中央带有穿透型预制裂缝的立方体或者圆柱体试件用于双K断裂参数的研究中，如图4所示，体现了正放立方体、斜对角立方体以及圆柱体三种形式，通过在试件顶、底部施加等值反向的力完成加载。

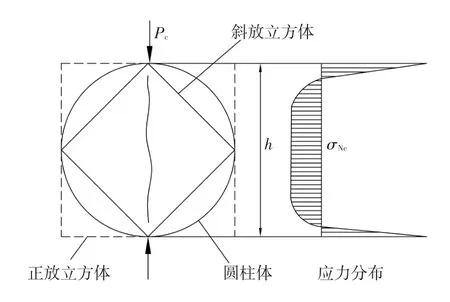
图4 立方体和圆柱体劈拉断裂试验

（5）近来，于菊瑶等［11］受前人启发，提出一种底部开裂缝立方体试件，通过在试件顶部中央施加集中力进行双K参数的测定，如图5所示。

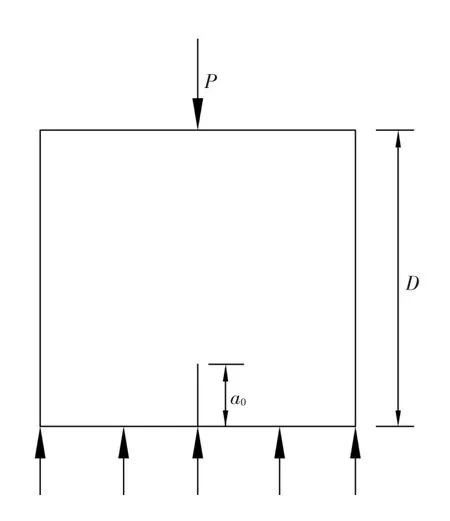
图5 底部开缝立方体劈拉试件

（6）Malik［12］首次将常用于岩土材料的半圆形单边切口梁来测定混凝土的双K断裂参数，如图6所示。

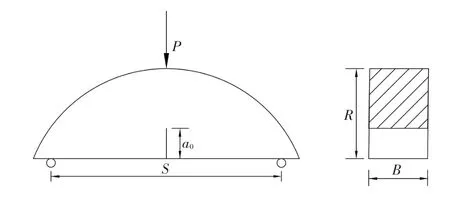
图6 半圆形单边切口梁示意图

（7）胡少伟等［13］考虑到裂缝扩展路径在三点弯曲梁中产生偏斜时存在剪力作用，进而会受到II型断裂分量的影响，因此开展了基于四点弯曲梁的研究，如图7所示。

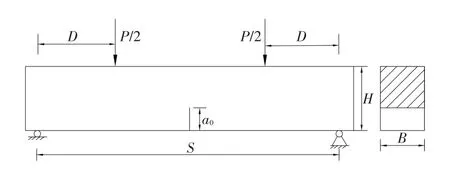
图7 四点弯曲梁示意图

其中，三点弯曲梁试验对设备刚度要求低，无需复杂加载装置，但试件自重大，搬运过程易对预制缝造成损伤。紧凑拉伸试件能够避免三点弯曲梁试件的自重对搬运与计算产生的不利影响，但在试验时对中困难，设备刚度要求严格，水平加载的方式在一般实验室不易实现和控制，为了适用于钻芯取样，种法橙提出了改进的圆形紧凑拉伸试件。楔入劈拉试验易对中，对试验机刚度要求较低，同样可以避免试件自重对于试验结果的影响，但当试件所产生的竖向分力与自重、支座反力不共线时，由此产生的附加弯矩会影响断裂韧度的计算结果。中央带有穿透型预制裂缝的立方体或者圆柱体试件形式简单、重量轻，制作搬运时不易损坏，既便于实验室浇筑又易于对现有结构进行钻芯取样。底部开裂缝立方体试件具有制备简单、操作方便的优点，适用于实验室和实际工程中混凝土双K参数的快速测定。半圆形单边切口梁试件尺寸小、节省材料、加工相对简单。但由此计算所得的双K断裂参数受试件尺寸影响较大。四点弯曲梁由于跨中裂缝截面附近处于纯弯区段，从理论上来说，此类试件更符合I型断裂特点。

2.2 确定方法

建立混凝土断裂判据，评价裂缝的稳定性与结构的安全性，首先需要正确地计算混凝土断裂参数。起裂韧度表示裂缝开始发展时材料抵抗外力的能力，此时荷载为Pini，裂缝长度为a0。失稳韧度是最大荷载时刻材料抵抗外力的能力，此时荷载为Pmax，裂缝长度为ac，现有的计算方法有：

（1）直接测定法。从理论上来说，获得双K断裂韧度只需分别把（Pini，a0）和（Pmax，ac）代入线弹性断裂力学公式即可，因此直接测定法需要试验确定Pini、a0、Pmax、ac的值。一般情况下，初始裂缝长度为已知数，Pmax、ac的值可以依据弹性等效原理，利用实测的荷载-位移（P-δ）曲线或者荷载-裂缝口张开位移曲线（P-CMOD）曲线得以获取，所以直接测定法的关键在于起裂荷载Pini的值。目前，确定起裂荷载Pini可通过光弹贴片法、声发射法、激光散斑法、电阻应变片法、初始缝高法等方法测定，还可通过曲线法读取。

（2）双K解析法。混凝土作为准脆性材料，在其裂缝尖端存在着断裂过程区，因此造成了混凝土断裂性能的非线性特征。荷载到达最大值时，裂缝长度由初始的a0增长到临界值ac，在双K断裂理论下，ac为a0与虚拟裂缝（断裂过程区）Δac之和，由此可见，起裂韧度、失稳韧度不是相互独立的，他们的差值是虚拟裂缝（断裂过程区）上骨料咬合黏聚作用的结果，三者存在下述关系：

（3）线性回归法。不同于直接测定法与双K解析法，线性回归法［14］是一种全新的方法。荷载-裂缝口张开位移曲线P-CMOD曲线在开裂后呈现非线性趋势，而在裂缝开裂前为线性，因此卿龙邦等采用线性相关系数陡降法，基于线性回归原理确定混凝土的起裂荷载。通过MATLAB对试验数据线性拟合，对拟合的P-CMOD曲线上升段的前k个点进行线性回归分析，确定线性相关系数r，由数学知识确定r-CMOD曲线上的陡降点，即为P-CMOD曲线由线性转为非线性的临界点，此点对应的P为起裂荷载Pini，代入线弹性断裂力学公式即可求得起裂韧度。

（4）峰值荷载法。研究以三点弯曲梁试件为例，Kumar等［15］提出了计算双K断裂参数的峰值荷载法。选定多组（至少3组）不同缝高比，或多组不同尺寸试件。通过线弹性断裂力学中的公式得到失稳韧度与裂缝尖端张开位移CTODC的关系，绘制各组试件与CTODC的关系曲线，与各组试件CTODC平均值的关系曲线，以及S（）（各组试件的标准差）与的关系曲线，并将S（）值最小所对应的作为材料参数，再利用式（1）反算得到起裂韧度

（5）极值荷载法与简化极值荷载法。与极值理论相结合，Qing和Li等提出了起裂韧度的极值荷载法［16］。依据文献［17］、［18］，得到外荷载P与有效裂缝长度a的关系曲线，见式（2）。如图8所示，假设P对a的导数在P=Pmax处连续，则可以认为该点处导数为0，详见式（3）。接着以紧凑拉伸试件为例，根据起裂韧度扩展准则［19］以及权函数表达式，得到外荷载表达式，基于Paris［20］公式求得裂缝尖端张开位移CTODC的表达式，再与式（2）和式（3）相联立，利用Qing和Li编制的MATLAB程序，数值计算求解得到起裂韧度。

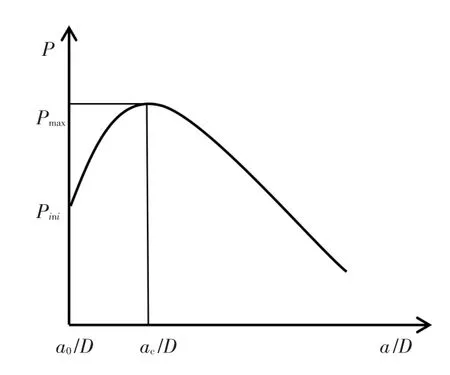
图8 混凝土断裂过程的荷载-有效裂缝长度（P-a）关系曲线

Qing等［21］又以楔入劈拉试件为例提出了失稳韧度的极值荷载法。在已知的前提下，临界有效裂缝长度ac可通过式（3）由迭代计算得到，接着用ac计算出临界状态下的裂缝尖端张开位移CTODC与最大荷载Pmax，再将各参数代入到失稳韧度计算公式中得到结果［22］。经与其他文献结果对比表明，在已知起裂韧度的基础上，该方法可以较准确预测构件的最大荷载Pmax及失稳韧度。

文中以三点弯曲梁为例，Qing等在考虑试件自重对于断裂韧度影响的前提下再次提出了一种简化的极值荷载法［23］计算材料的断裂韧度。利用得到的三点弯曲梁试件外荷载P的表达式，与式（2）、式（3）联立得到仅含有ac一个未知变量的等式。将ac代入相应公式求出起裂韧度与失稳韧度。相比之下，简化极值法在计算过程中更加简便，避免了复杂的数值积分。

双K解析法需要试验测定最大荷载Pmax和临界裂缝口张开位移CMODC这2个重要参数，直接测定法则还需试验获取起裂荷载Pini，因此对试验的准确性依赖较高，然而由于混凝土自身骨料的不均匀性，试验所测参数不免存在误差。极值荷载法、简化极值荷载法与峰值荷载法，均只需试验测定Pmax，只是极值荷载法涉及复杂的积分运算，计算难度大，峰值荷载法所需试件数目较上两种偏多，线性回归法目前仅用于计算起裂韧度，具有较高的精确度，无需粘贴应变片，也没有复杂积分运算，由此法计算所得的Pini与试验测定的相差不超过10%。峰值荷载法计算的失稳韧度较双K解析法的结果偏小，平均误差不超7%，起裂韧度稍大于双K解析法的结果。由双K解析方法计算得到的断裂参数略小于极值荷载法的结果，略大于简化极值荷载法的结果。

直接测定法需在试验中测定荷载与裂缝口张开位移，进而代入线弹性力学中的应力强度因子表达式计算得出起裂与失稳韧度；双K解析法则是基于应力强度因子的叠加原理，计算断裂过程区的黏聚韧度之后在已知失稳韧度的基础上间接求得起裂韧度；线性回归法基于线性回归原理确定起裂荷载Pini，之后代入相关公式计算起裂韧度，由此方法计算的起裂韧度经验证不存在明显的尺寸效应；峰值荷载法的计算离不开复杂的数值积分，普及难度大；基于极值理论的极值荷载法与简化极值荷载法均利用了临界状态时荷载-有效裂缝长度曲线的导数为0的特点，仅需测量峰值荷载，无需试验测量裂缝口张开位移，便可求得起裂韧度，并且简化法还避免了复杂的积分计算。

2.3 影响因素

为了验证双K断裂参数是否存在尺寸效应，以及受其他影响因素的制约程度与变化规律，众多学者进行了大量工作。

学者们通过对不同高度的三点弯曲梁试件［24］、紧凑拉伸试件［25］、楔入劈拉试件［26］，不同宽度的三点弯曲试件［27］、不同初始缝高比的楔入劈拉试件［28］、三点弯曲梁［29］进行断裂试验以及不同缝高比三点弯曲梁［30］的模拟，研究双K断裂参数受试件尺寸的影响程度，综合上述分析结果来看，高度大于200mm的三点弯曲梁、紧凑拉伸试件，高度大于600mm的楔入劈拉试件，计算所得双K参数未表现出尺寸效应；三点弯曲梁宽度在试验设计的80～160mm范围内时，双K参数随宽度增大而增大；缝高比的变化未引起显著的断裂参数变化，对于初始缝高比接近0.8～0.9时，所测试件的起裂韧度近似等于失稳韧度。

针对不同强度等级的三点弯曲梁，试验结果［31］与模拟结果均显示双K断裂参数随强度等级的提高而增大。

研究不同骨料粒径的楔入劈拉试件［32］断裂参数发现，当最大骨料粒径小于40mm时，起裂韧度与失稳韧度随着骨料粒径的增大而增大，当大于40mm，双K参数随骨料粒径增大反而下降。

除此之外，学者们对高温作用后［33］、硫酸盐侵蚀环境下、冻融影响下的混凝土断裂行为也进行了探讨，结果表明试验中的双K断裂韧度受到以上外界因素的影响均有所下降［34，35］。

当试件高度足够大时，双K断裂参数的尺寸效应不明显，即与试件的几何尺寸无关。而最大骨料粒径、试件强度、温度、冻融、硫酸盐侵蚀等均会影响断裂韧度的值。

2.4 延伸准则

受双K准则的启发，赵艳华等［36］利用断裂力学中的能量法，结合虚拟裂缝模型，以能量释放率G作为表征混凝土断裂特性的参数，从而建立了以起裂韧度和失稳韧度作为混凝土起裂与失稳判据的双G准则。并利用分布在断裂过程区上粘聚力的局部耗能将二者联系起来，建立了起裂韧度和失稳韧度的计算公式。

基于双K断裂准则，吴智敏等提出了混凝土I型裂缝扩展准则，该准则认为混凝土裂纹尖端的起裂引起了每一次裂纹的扩展，判断每次起裂的标准则是起裂韧度整个构件的断裂过程便由这样若干次的起裂构成。具体可表述为：①裂缝不扩展裂缝处于临界状态；③裂缝扩展。其中，KIp为外荷载P引起的裂缝尖端应力强度因子，KIσ为粘聚力引起的裂缝尖端应力强度因子。基于此准则，能够实现对混凝土断裂的全过程模拟。

双G与双K断裂准则都是依据修正后的线弹性断裂力学对裂缝的发展过程进行判定，具备一定的等效性，按两种方法计算所得断裂韧度值接近。文献［19］的模型认为裂缝扩展的每一步均需满足起裂准则，即，裂缝扩展，而双K准则认为只在初始裂缝长度处起裂满足起裂准则；另外，文献［19］假设断裂过程区上各点应力大小均满足拉伸软化曲线，而双K模型将断裂过程区的应力简化为线性分布。

2.5 理论应用

近年来，双K准则不仅应用于类混凝土材料断裂行为的研究，在分析大体积混凝土裂缝的稳定性，确定带裂缝结构的可靠度方面也做出了突出贡献。

水泥净浆和水泥砂浆、超高强混凝土、聚丙烯纤维混凝土、锂渣再生混凝土、以及海水海砂混凝土等［37-41］多种非脆性材料基于双K准则的断裂行为得到了学术界的关注与探究。

作为国内首批“西电东送”工程之一的乌江索风营水电站，当年基于双K断裂准则开展裂缝控制与评价，采取了相应的裂缝控制技术，至今已安全运行10多年，属国内同类坝体裂缝较少的工程［42］。双K断裂理论同样在三峡三期工程混凝土施工中发挥了重要作用，基于双K准则对混凝土配合比进行优化，同时提出了相关技术和工艺改善施工过程，取得了良好的成效。此外，通过对丹江口大坝［43］钻芯取样，在试验室测定试件的双K断裂参数，对大坝上游由于某次温度骤降引起的多处竖向裂缝进行了水压力作用下的稳定性分析，并给出了排水处理的建议，为大坝安全评估和修复提供了科学依据。

3 结语

通过总结国内外学者在试件形式、确定方法、影响因素以及理论延伸和应用方面对双K准则的研究成果，得到以下主要结论：

（1）由于现有试件形式尚存在不足之处，因此对试件形式的研究仍将继续，对于改进的圆形紧凑拉伸试件、底部开裂缝立方体试件、半圆形单边切口梁以及四点弯曲梁在测定双K断裂参数方面的广泛适用性仍需探讨。

（2）双K参数的确定方法中有关黏聚应力分布模型适用性，对拉伸软化曲线以及试件尺寸的敏感性等问题可做深入讨论与对比。在合理可靠的范围内，确定方法定会朝着计算过程简化，试验难度适中，人为误差小的目标不断改进与创新。

（3）随着试验技术的发展及学科间的交叉融合，复杂环境下结构裂缝的稳定性评价与预测，高性能混凝土材料的研制与改善，地震作用下混凝土动态断裂韧度的确定，以及从中细观层次分析断裂问题，理解试件从微裂纹萌生、扩展、贯通直到宏观裂纹产生，导致混凝土破坏的全过程也将迎来更多的重视。

自双K准则及其相关计算理论提出至今，取得了诸多成果，并日趋成熟，得到了学术界与工程界的共同认可。相信通过各国学者的努力与探索，双K准则必将在裂缝的安全评估与预测方面发挥重要作用，并推动新型混凝土材料与复杂环境下的断裂问题研究取得更加丰富的成果。