机压滴灌管网优化设计与应用

宋 博, 钱治丞, 赵 冰, 曲 颂

(黑龙江大学 电子工程学院， 哈尔滨 150080)

0 引 言

滴灌具有减少输水损失、节约土地、适用于各种不同地形和管理运行方便等优点，被广泛用于农田灌溉中[1-3]。目前，实际滴灌项目的管网设计主要凭借设计者经验，缺乏对设计方案的优化和比较，导致管网投资成本较高。因此，研究管网的优化设计方案，可有效地降低项目投资，进一步推动农田灌溉事业发展。管径的组合方式对管网投资影响很大，优化此部分投资得到的经济效益也更显著[4]。管径优化的传统方法包括线性规划法[5]、非线性规划法[6]和枚举法[7]等，采用这些方法进行优化时，会受到管网规模的限制。当管网复杂且规模较大时，待求解的管段数量较多，若利用此类解析法求解，存在计算时间过长或在规定时间内得不到最优解的问题。近些年，计算机技术发展较快，遗传算法(Genetic algorithm, GA)[8]、粒子群算法(Paticle swarm optimization, PSO)[9]和荧火虫算法(Firefly algorithm, FA)[10]等被用于求解管径优化问题并取得了一定的效果。虽然这些算法存在局部寻优能力不强和搜索效率低等问题,但萤火虫算法在解决实际工程问题及组合优化问题中表现优异，优化结果的准确性和可靠性都优于GA算法和PSO算法[11]。因此，本文针对萤火虫算法在解决管网优化这种复杂问题时，存在易陷入局部最优的缺陷进行了改进，采用改进后的算法解决滴灌管网优化问题。

1 改进萤火虫算法

1.1 基本萤火虫算法

萤火虫算法(FA)由Yang于2008年提出，该算法主要依据在搜索空间中，绝对亮度小的萤火虫个体被绝对亮度小的萤火虫吸引并向其移动这一特点实现寻优[12]。FA搜索过程与萤火虫个体的亮度和吸引力参数有关。萤火虫i对萤火虫j的相对亮度为：

Iij(rij)=Iie-γrij2

(1)

式中：Ii为萤火虫i的绝对亮度；γ为光吸收系数；rij为萤火虫i到萤火虫j的距离，即：

(2)

萤火虫i对萤火虫j的吸引力表示为：

βij(rij)=β0e-γrij 2

(3)

式中β0为最大吸引力，即在光源处萤火虫的吸引力。

寻优过程中，萤火虫j被萤火虫i吸引，向其移动的位置更新过程为：

(4)

式中：t为迭代次数；xi(t)为萤火虫i所处的空间位置；xj(t)为萤火虫j所处的空间位置；α为步长因子；Rand为[0,1]上服从均匀分布的随机因子。

1.2 改进萤火虫算法

由于萤火虫算法在求解复杂优化问题时，存在收敛速度慢和易陷入局部最优的缺点，因此对萤火虫位置的初始化、随机步长以及全局最优位置进行了改进。

1.2.1 萤火虫位置初始化的改进

在萤火虫算法中，萤火虫被随机散布在待优化问题的解空间，很可能使得个体初始位置分布失衡，个体容易落入局部最佳位置，导致算法寻优效果不佳。采用立方映射生成的混沌序列[13]初始化种群位置，混沌序列表达式为:

y(n+1)=4y(n)3-3y(n)

(5)

式中：y(n)∈[-1,1],y(n)=0,1,2,…。

萤火虫种群的初始化进行混沌改进的过程如下：首先，在萤火虫种群的d维空间中，随机生成一个d维向量X作为萤火虫个体的第一个初始位置，即X=(x1,x2,…,xd)，其中Xi∈[-1,1]。然后，对向量X的每一维，按照式(5)进行迭代，生成剩余萤火虫个体的初始位置。最后，将上述步骤产生的萤火虫个体的初始位置按照式(6)与搜索空间中的解进行一一映射。

yid=Ld+(1+xid)(Ud-Ld)/2

(6)

式中：Ud和Ld分别为搜索空间中的上限和下限；yid为搜索空间中个体i在第d维的取值；xid为种群中个体i在第d维上的取值。

1.2.2 随机步长的改进

标准萤火虫算法中随机步长是固定值，若使算法同时拥有较好的寻优速率和寻优准确度，很难为其确定一个恰当的值。采用动态步长的搜索方式可以使得算法的寻优能力更加均衡，采用随迭代次数非线性递减的方式可以对随机步长进行改进。

(7)

式中：k0为步长衰减系数；α(t)为初始步长；Tmax为最大迭代次数。

1.2.3 高斯变异策略

萤火虫算法尽管在个体位置更新迭代中添加了随机扰动项，但是在求解高维、多峰等复杂的优化函数时，算法依然容易陷入局部最优，这是由于个体缺乏变异能力。本文引入改进的高斯扰动，即在萤火虫更新迭代的过程中，对每一代搜寻到的最优位置Gbest按照式(8)进行高斯扰动，将得到新的全局最优位置Ngbest按式(9)进行更新。

(8)

(9)

1.3 仿真实验

为验证改进萤火虫算法的有效性，选取表1中4个基本测试函数对所提出的改进萤火虫算法、标准萤火虫算法和遗传算法进行算法性能的验证和比较。在算法的参数设置中，3种算法的种群规模均为40，基本测试函数的维度为30维，算法的最大迭代次数为200次。遗传算法中交叉概率为0.60，变异概率为0.80；改进萤火虫算法和标准萤火虫算法中最大吸引力系数β0=1，光吸收系数γ=1，初始迭代步长α=0.5。将算法对每个测试函数独立运行30次，求取运行30次的最优结果的平均值，确保测试结果的可靠性和稳定性。

表1 测试函数参数设置

测试函数的仿真结果如图1所示。Sphere函数的收敛曲线如图1(a)所示，改进算法在迭代10次左右就能快速地收敛到全局最优解,标准萤火虫算法需要60次迭代左右才能找到最优解。遗传算法收敛速度最慢，最终陷入了局部最优。Rosenbrock函数的收敛曲线如图1(b)所示，萤火虫算法和遗传算法相继陷入不同的局部最优区域，而改进萤火虫算法则能较好地平衡全局搜索能力和局部挖掘能力，找到相对较优的收敛区间，但最终算法依然陷入了局部最优。Rastrigin函数和Griewank函数的收敛曲线如图1(c)和图1(d)所示，改进萤火虫算法在迭代10次左右就能达到全局最优，遗传算法和萤火虫算法在规定的迭代次数内仍未搜索到全局最小值，陷入了局部最优状态。以上对测试函数的仿真实验证明，改进萤火虫算法具有较好的平衡算法开发和探索能力，适合求解复杂函数优化问题。

(a) Sphere函数的收敛曲线

2 滴灌管网设计

2.1 基础理论

机压滴灌系统由水源工程、首部枢纽、输配水管网和田间灌水器构成，其中输配水管网可分为骨干管网和田间管网。管网设计可对田间管网和骨干管网分别设计，在明确各项设计参数后，进而对管网的布置、灌水方案、各级管道流量、各级管道直径、系统水头损失及水泵参数进行确定。管网布置主要确定干管、支管和毛管的铺设长度。实际工程和普遍采用轮灌方式灌溉，轮灌分组应满足供水情况。在确定管道水头损失时，应根据《微灌工程技术标准》中的勃拉休斯公式进行计算：

(10)

式中：hfi为第i段管道的水头损失，m；f为摩阻系数；Qi为第i段管道流量，L·h-1；m为流量指数；b为管径指数；Di为第i段管道直径，mm；L为管道长度，m。

在实际项目中，骨干管网设计对管网投资影响很大，设计者对管径型号的确定普遍使用常规的经济流速法，利用该方法计算的管径通常不能满足标准管径，需进一步选取和计算管径值相近的标准管径，得到的结果，通常不是最优设计方案，管网投资较高。因此，对骨干管网进行优化设计，有利于降低管网建设成本和水泵运行成本，下面通过建立一个优化模型来描述骨干管网的优化设计问题。

2.2 优化模型

骨干管网投资通常包括管网基建费和水泵运行费[14]。当管道中压力和水量一定时，管径细则投资少，但管中流速大，水头损失大，水泵年运行费增大；粗管径情形则正好相反[15-16]。因此，为寻求最优管径组合与水泵扬程的设计方案，使得骨干管网年费用最低，建立以干管及分干管各管段管径、水泵扬程为决策的函数模型：

(11)

管径约束：上级管径应不小于下级管径，且各级管道上一段管径不小于下一段管径：

Di≥Di+1

(12)

流速约束：为防止水流在管道中产生较强的水锤作用，要求管内流速应满足以下条件：

Vmin≤Vi≤Vmax

(13)

(14)

因此，可得：

(15)

工作压力约束。在水泵的工作范围内，应保证在最不利灌溉制度下最不利工作点的灌水器能够正常工作，即达到额定工作压力，水头应满足以下条件：

(16)

H≤αHd

(17)

式中：W0为滴灌系统年费用，元/年；s为年利率，%；t为管网折旧年限，年；P为管网维修费率，%；n为各级管网的管段总数；a1、b1为管径与单价拟合系数；Di为第i个管段选用的标准管径，mm；Li为第i个管段选用的标准管径的长度，m；E为电费，元/kW·h；T为系统年工作时数，h；H为水泵扬程，m；Q为灌溉系统首部输出流量，m3·h-1；η为水泵工作效率，%；Vi(k)为第i段管道流速，m·s-1；Vmin为系统中允许通过的最小流速，m·s-1；Vmax为系统中允许通过的最大流速，m·s-1；hfi和hgi分别为第i段管道沿程水头损失和局部水头损失，m；Hw为灌水器工作水头，m；ΔHs为灌溉首部与灌溉末端的地面高程差，m；Hd为管道承压，m；α为安全系数。

2.3 模型求解方法

测试函数的仿真实验证明，改进萤火虫算法较标准萤火虫算法和遗传算法在函数优化问题上具有明显优势，适合解决滴灌管网这样的复杂优化问题。因此，应用改进的萤火虫算法对建立的模型进行求解，具体求解步骤为：

(1) 编码

管径组合从标准商用管材中选择，供选择的管径型号是确定的离散值，本算法采取整数编码方式，将一系列标准管径映射为一组整数值，参数编码如表2所示。水泵扬程采取实数编码，编码值为真实值。

表2 管径参数编码表

(2) 适应度函数

多约束问题选择引入罚函数的方法将约束问题转为非约束问题。对骨干管网年费用最低的适应度函数为：

(18)

(19)

式中M1和M2为惩罚因子。

(3) 改进萤火虫算法的迭代寻优

每只个体的位置代表一个可行的设计方案，个体的最大闪光亮度代表适应度函数值，即管网年投资费。根据改进萤火虫算法的优化原理，计算目标函数值，通过不断更新个体位置和亮度，在给定管径及价格等集合中多次迭代寻优得到管网年费用最小值。

3 工程应用

3.1 工程概况

项目区地处黑龙江省西部大庆市杜尔伯特自治县，地理坐标为北纬45°23′～45°59′，东经123°47′～125°45′。灌溉区域地势平坦，地块形状规则，底宽约108 m，长约330 m，面积约55亩。土壤类型主要为中壤土，种植作物为枸杞。作物株距0.3 m，行距1.5 m。灌溉水源为井水，由泵站加压抽水、过滤后经管道输送至田间。水井位于地块东南侧，抽水试验结果表明，当动水位下降至地下20 m时，出水量为30 m3·h-1。

3.2 滴灌系统主要设计参数

根据项目区实际情况，确定滴灌系统各项设计参数，如表3所示。

表3 研究区滴灌设计主要参数

图 2 骨干管道布置图

3.3 滴灌系统布置

针对滴灌工程布置中树状管网的应用广泛性，工程选择树状管网布置形式。管网由主干管、分干管、支管和毛管四级管道构成，干管、分干管及支管均采用PE材质承压给水管，干管和分干管的管道承压力为0.63 MPa。主干管及分干管埋设在地下，支管及毛管铺设于地面。一条支管与其控制的毛管构成一个灌水单元，由支管入口的电磁阀统一控制。每两个支管轮灌单元共用一个出水立管与地埋分干管相连。项目区骨干管道采用“丰”型布置，主干管从首部接出，垂直布置在地块中央，分干管垂直干管，对称分布在干管两侧。毛管沿作物种植方向布置，支管垂直于毛管布置。根据项目区作物种植情况，确定毛管采用内嵌贴片式滴灌带，直径16 mm，沿支管两侧对称等长布置。具体布置形式如图2所示。根据地形特点，综合项目区地块宽度，考虑工程实际施工影响，通过计算毛管极限长度并根据设计人员经验确定毛管、支管长度及对干管位置进行定位，得出毛管单侧长度为Lm=55 m，支管长度Lz=27 m。毛管和支管长度初步确定后即可确定干管和分干管的长度及定位。

3.4 滴灌系统工作制度

采用支管轮灌的工作制度，轮灌组数为N≤Nmax=INT[CT/t]=6，取N=6。考虑项目前期对各个轮灌组中电磁阀的控制有农户到现场手动控制的方式，因此，为了便于农户田间运行管理，减少人力，应当对每种布置方案确定轮灌分组时，将同一条分干管上相邻的2条支管划分为一个轮灌组。具体轮灌安排如表4所示，以此轮灌顺序进行优化研究。

表4 系统轮灌制度表

3.5 优化设计

管径组合从滴灌工程中常用的国家标准规格的管材中进行选择，标准管道价格如表5所示。根据表5中数据采用最小二乘法进行管道造价回归拟合，得到相应的管道造价拟合图，如图3所示。由管道造价拟合曲线，得到管道造价公式y=axb，即a1=0.283 8，b1=6.449 9。

表5 管道管径及造价

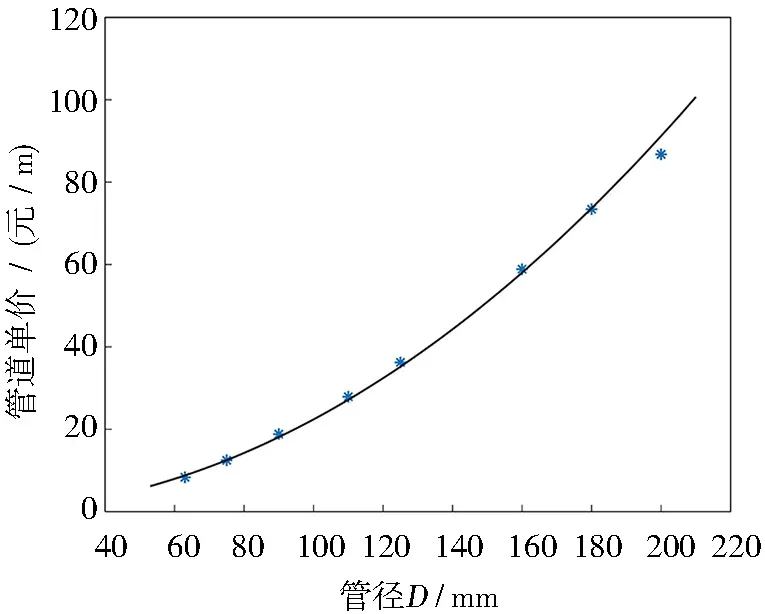
图3 管道单价系数拟合图

根据优化程序，将各部分数据代入模型进行优化计算。萤火虫种群规模N设置为20，迭代次数M设置为100，光吸收系数γ设置为1，初始步长α设置为0.5，M2设置为30，M1设置为10。管网折旧年限t取10，年利率r取0.03，管网综合维修费率P取0.02，电费E取0.6元，水泵工作效率η取0.76。优化过程如图4所示。可以看出，应用改进萤火虫算法进行管径优化时，曲线随着迭代的进行逐渐下降，证明目标函数即管网年费用随迭代过程逐渐降低，管网优化模型运行正常。曲线最终趋于平衡，证明改进算法能够有效地对管道直径进行筛选和优化，得出满足约束条件的最优解，验证了改进算法在求解管网优化问题的有效性，表明此方法是实现管网优化模型快速求解的一种新途径。

3.6 优化结果与分析

根据模型应用结果，将使用改进算法优化后的设计方案与常规经济流速法得到的设计方案及系统投资进行比较，计算对比结果如表6和表7所示。常规经济流速法设计的骨干管网年费用为1 851元，管网基础投资为11 273元，采用改进萤火虫算法设计出的骨干管网年费用为1 042元，管网基础投资为6 930元，骨干管网年费用和管网总投资较常规经济流速法分别节约了43.71%和38.53%。管网投资降低明显，证明了改进的荧火虫算法求解滴灌管网工程设计方案是可行有效的。

表6 骨干管网管径优化结果

表7 骨干管网投资对比表

4 结 论

针对萤火虫算法容易陷入局部最优和优化精度不高的问题，对萤火虫算法进行了改进，将立方映射和高斯变异引入标准萤火虫算法中，提高了算法收敛速度和求解精度。建立了机压滴灌系统骨干管网优化设计的数学模型，采用改进的萤火虫算法进行求解，得到年费用最低的管径最佳组合方案及水泵扬程。工程实例表明，改进萤火虫算法的优化设计方案与传统经济流速法的设计方案相比，骨干管网年费用及基础投资分别降低了43.71%和38.53%，节省投资效果明显。