矩阵型因子模型及其在我国省际人口流动网络数据中的应用

王浩莹, 徐赛男, 王亚杰, 马维军, 袁超凤

(黑龙江大学 数学科学学院, 哈尔滨, 150080)

0 引 言

高维矩阵值时间序列数据广泛存在于金融经济学、气象水文和图像处理等许多领域。这类数据复杂度高，特点难以发现，因此，对高维矩阵值时间序列数据进行分析并寻找规律具有十分重要的意义。

近年来，针对高维矩阵值时间序列数据，众多学者进行了相关研究[1-4]。2019年，Wang等提出了一个矩阵型因子模型。该模型在保证了数据的矩阵结构的同时，实现了显著的降维[1]。2019年，Chen等基于上述模型通过对行和列施加线性约束，并将先验知识融入到了模型中，从而增强了观测矩阵中潜在因子的可解释性[5]。2020年，Chen等给出了上述矩阵型因子的另一个应用研究，即用在动态国际贸易数据上。由于国际贸易数据可以被整理为一个动态网络数据，也可视为矩阵型时序数据[6]。2019年，Yu等针对上述矩阵型因子模型给出了一个投影估计方法，并证明了其投影估计有较高的收敛阶数[7]。2020年，Chen等进一步考虑了上述矩阵型因子模型的统计推断问题[8]。

针对上述矩阵型因子模型，给出了模型可识别的充分条件，并从拟似然的角度给出了一个新的参数估计方法。最后，将上述模型应用于我国31个省(包括4个直辖市)之间的人口流动网络数据，研究其网络结构的动态变化规律。

1 矩阵型因子模型

1.1 模型介绍

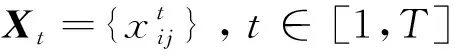
Xt=RFtC′+Et

(1)

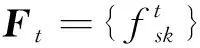
vec(Xt)=(C⊗R)vec(Ft)+vec(Et)

(2)

基于上述模型便可将高维观测矩阵Xt在时间上的相依性用更低维(k1×k2)的因子矩阵来驱动，达到降维的目的。

1.2 可识别性研究

Σ=(C⊗R)ΣF(C′⊗R′)+σ2Ip⊗Iq

(3)

定理1设θ={R,C,ΣF,σ2}为所有参数，在模型假设(IC1)和(IC2)的条件下，模型(1)的协方差阵结构(2)式满足可识别，即由Σ(θ)=Σ(θ*)，可得θ=θ*。

1.3 矩阵型因子的拟似然估计

对于传统的向量型因子模型,2015年，Ng等利用矩阵分解得到了参数的拟似然估计[11]，2016年，Bai等利用两步拟似然法求出了估计，并证明了拟似然估计在一定条件下满足相合性，且具有理想的收敛速度[12]。针对矩阵型因子模型(1)，将通过拟似然的方法(Quasi-maximum likelihood estimation, Q-MLE)，对其参数进行估计。

(4)

则E(MXX)=Σ。因此，构建如下的拟似然函数：

L(θ)=-log|Σ|-tr(MXXΣ-1)

(5)

由Σ的特殊结构(如式(3))，可以求出其逆矩阵及行列式的显式表达式(见定理2)，从而可对上述拟似然进行化简。

定理2假设Σ=(C⊗R)ΣF(C′⊗R′)+σ2Ip⊗Iq，且满足R′R=pIk1；C′C=qIk2，则其逆和行列式为：

由定理2，拟似然函数可化简为：

(6)

接下来便通过以下三步分别给出R,C,{ΣF,σ2}的估计。

(1)给定C、 {ΣF,σ2}及R′R=pIk1, 求R的估计。

通过简单的矩阵运算，式(6)可化简为：

(7)

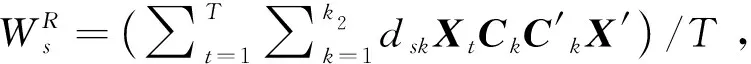
表1 更新R为

(2)给定R、{ΣF,σ2}及C′C=qIk2，求C的估计。

方法与求R的估计类似，化简拟似然函数式(6)为：

(8)

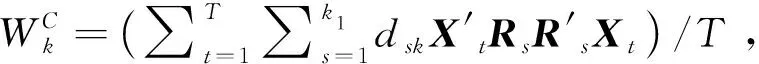
(3)利用EM算法，估计{ΣF,σ2}。

设θ1={ΣF,σ2}，给定R和C，可以通过EM过程进行估计。令完全的拟似然函数为：

(9)

进一步在正态假设下可得潜在因子的条件分布为：

vec(Ft)|vec(Xt)～N(μ,Δ)

(10)

其中μ=ΣF(C′⊗R′)Σ-1vec(Xt)，Δ=ΣF-ΣF(C′⊗R′)Σ-1(C⊗R)ΣF, 则Q函数为:

(11)

最大化Q函数有:

(12)

(13)

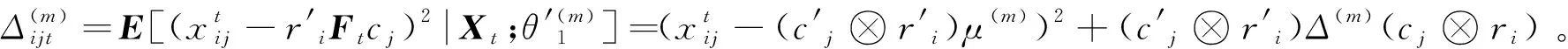
综上三步，采用如下的交替最大化算法来估计参数，如表2所示。

表2 交替最大化算法

2 模拟研究

将通过数值模拟来验证上述拟似然估计的有效性，并与文献[1]给出的估计方法进行比较。

2.1 数据生成

根据模型(1)生成观测数据Xt，其步骤如下：

(4) 观测数据Xt通过式(1)生成。

分别考虑了k1=k2=1、k1=k2=2及p,q,T=20, 50, 80, 100的情况，每种情形下重复500次。

2.2 模拟结果

表3呈现了k1=k2=1时参数的估计结果。其中，σ2=1，Φ=0.55，则因子的方差ΣF=1.433 7。由表3可以看出，随着p、q和T的增加，两种参数的估计效果逐渐变好，且采用的估计方法始终优于文献[1]中的方法。此外，文献[1]中的方法仅能给出载荷矩阵的估计，而本文的方法不仅能给出载荷的估计，还能给出与方差有关的参数的估计。

表3 k1=k2=1的模拟结果

表4 k1=k2=2的模拟结果

3 人口流动网络数据实证分析

人口的迁徙流动一直是涉及地理学、管理学和人口学等学科的热门研究课题。目前，人口的流动也是国内新冠疫情扩散的主要原因[15-17]。本节将对由百度迁徙大数据平台得到的我国各省之间的人口流动网络数据进行分析，研究其网络结构的动态变化规律。

3.1 数据介绍与整理

本文数据来源于百度迁徙大数据平台(https://qianxi.baidu.com/)，该平台利用百度地图定位服务LBS(Location based service)，通过手机定位信息记录用户行为轨迹，记录出人口流动过程中的起止城市，路径流强度。研究数据包括从2020年10月1日到2021年8月29日(共330日)的逐日的31个省级行政区(包括直辖市和自治区，不含港澳台)之间的省际流动数据。初始数据包含关于每个省迁入、迁出人口的规模指数，和其迁入、迁出来源省份的比率。时间跨度包含2021年元旦前、春运和暑假。由于百度迁徙网站缺失7月8日、8月12日和8月25日的数据，故这三日忽略不计。

3.2 结果与解释

首先，对于每个窗口，利用文献[5]中的方法选出因子的个数，即k1,k2,结果如表5所示。同时，也列出了当k1=k2=3时的累计方差贡献率。对于每个窗口，当因子数k1=k2=3时，模型至少解释了总方差的80%以上。故为了便于解释和比较，对所有时间窗口均采用k1=k2=3来估计载荷矩阵R和C。

表5 因子Ft的维度的估计和k1=k2=3时的累计方差贡献率

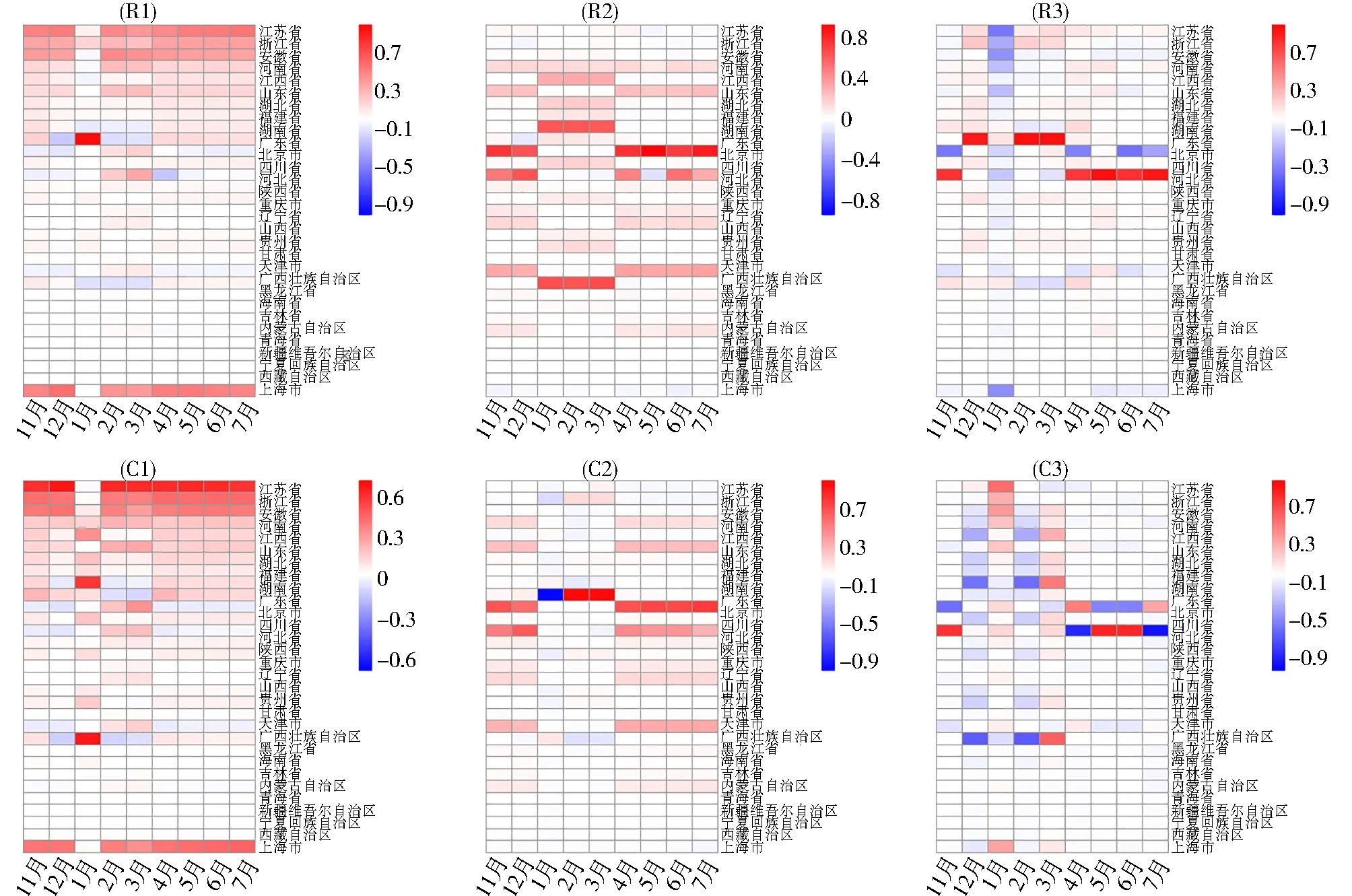
图1 因子个数为k1=k2=3时的载荷热图

观察图1中的(R1)，除1月以广东为主导外，其他窗口都是长三角(长江三角洲城市群)城市所在省，例如上海、江苏、浙江、安徽，占据了第1个迁出枢纽的主导地位。观察(C1)，除1月以外，长江三角洲城市群也占据了第1个迁入枢纽的主导地位。这与江浙沪皖三省一市经济实力最强，城市聚集程度高密切相关，从而使得人口的短期流动最为活跃。1月对应的窗口实际包含12月、1月、2月，包含春运期间，是以泛珠三角主要省份(湖南、广西、江西)为第1个迁入枢纽，以广东为第1个迁出枢纽。这与他们的地理位置及密切的经济往来相关。

图1中(R2, C2)可分为两部分，11～12月、4～7月分别是以北京为主导地位的京津冀(北京、天津、河北)地区为第2个迁出和迁入枢纽。1～3月则是以泛珠三角省份(湖南、广西、江西)为主的第2个迁出枢纽，同时也是以广东为主的第2个迁入枢纽。

由图1中的R3，从11月、12月、1月、2～3月、4～7月数据可知，第3个迁出枢纽依次由河北，变为广东，变为长三角、变为广东、变为河北。由图1中的C3，在上述时间段中，第3个迁入枢纽依次由河北，变为泛珠三角、变为长三角、变为泛珠三角，变为河北。

综合图1来看，山东、河南的人口流动情况较长三角、珠三角和京津冀都较弱，长三角省群枢纽主要分布在第一、三个枢纽，且在所有时间段上一直都是人口流动情况明显的省群，京津冀省群枢纽在第二、三个枢纽都占了比较明显的主导位置，主导时间主要是11～12月、4～7月，而珠三角省省群枢纽在一、二、三个枢纽中都占有较大载荷，主导时间主要是12～3月。

图2 潜在枢纽的人口流动网络图: (a) 2021年2月; (b) 2021年7月

观察图2，2月份、7月份的第1个迁出、迁入枢纽均为长三角省群。2月份的第2个迁出、迁入枢纽为泛珠三角省群，7月份以北京为主。2月份的第3个迁出、迁入枢纽为广东，7月份的为河北。由实线部分可以看出所有枢纽的内部人口流动性最强，比如迁出枢纽1与迁入枢纽1之间的实线最粗，说明长三角省群内部的人更偏好于在长三角流动，这是受地理因素影响比较大的原因。

最后，为了呈现省份间流动情况的相似性，分别基于2月份和7月份的载荷矩阵进行层次聚类(图3)。本文选取欧几里得距离和离差平方和法进行层次聚类[19-20]。图3(a)依次2月份R和C的结果，图3(b)依次为7月份R和C的结果。

由图3可以很容易地识别出长三角群体和珠三角群体。一般来说，地理位置相近、经济和文化联系密切的省份通常会属于一个群体，人口流动情况会相似。比如2月的广东、湖南和广西人口流动很活跃，故整个2月可标记为“珠三角活跃”、“长三角-京津冀活跃”和“不那么活跃”。而省份之间的关系也在发生变化，2月的珠三角在人口流动网络中占主导地位，而后京津冀在人口网络中越来越活跃，7月成为了一个单独的集群。此聚类图和图1、图2所说明的情况也相呼应，这也说明了本文的结果具有一定的可靠性。

图3 根据迁出和迁入载荷矩阵对省份聚类: (a) 2021年2月; (b) 2021年7月

4 结 论

为了更好地理解矩阵值时间序列数据的动态性质，本文针对文献[1]中所研究的矩阵型因子，提出了可识别性条件，并基于拟似然的参数估计方法，不仅求出了载荷矩阵的估计，还求出了潜在因子矩阵的估计。同时，通过模拟验证了所提出的估计方法在矩阵维数较大或者在时间长度较大时也是更具有优越性的。用所提出的估计方法针对人口流动网络数据进行了分析，研究其网络结构的动态变化规律，研究结果能为中国省际人口流动的动态性研究提供一种新型的可参照方法。

本文所用的高维矩阵型时间序列模型可以更直观地呈现出网络型数据的动态性变化。由于并没有对网络模型提出任何分布假设，所得到的载荷矩阵和潜在因子矩阵也都是直接从数据网络中得到的，而且所提出的方法可以有效地降低动态网络的维数，并揭示其核心结构，得到的载荷矩阵的估计和潜在因子的估计可以进一步用于动态型网络数据的研究和预测，也可以广泛运用到其他动态因子模型。