一种优化的灰狼算法

杨寒石, 吴皓月, 孔德贵

(1.黑龙江大学 电子工程学院, 哈尔滨 150080; 2.黑龙江大学 计算机科学技术学院, 哈尔滨 150080)

0 引 言

传统灰狼算法(Grey wolf algorithm，GWA)是一种模拟狼群狩猎行为的智能算法，已经广泛应用于无人机航路规划和电机控制等研究领域[1-4]。然而，GWA算法存在局部开发能力较弱、早熟收敛和初始种群分布不均匀等问题。针对这些问题，学者们主要从种群初始化、控制参数、狼群搜索机制以及灰狼位置更新策略等方面对GWA算法进行了优化[5-7]。2015年，Saremi等将进化种群动态算子(Evolutionary population dynamic, EPD)引入到GWA算法中，显著提高了算法的局部搜索能力和收敛速度[8]。2017年，龙文等采用佳点集法替代GWA算法中利用随机数初始化种群的方法，增加了初始种群的多样性[9]。2020年，甄永琦等将差分进化算法(Differential evolution algorithm，DEA)与GWA算法相结合，利用DE算法的交叉算子和变异算子改进灰狼位置更新公式，提高了GWA算法的局部开发能力[10]。2020年，刘彬等利用竞争策略动态更新α狼、β狼和δ狼的位置，提高了GWA算法的全局搜索能力[11]。2021年，王颖等结合云模型理论，通过动态权重法调整收敛因子，平衡GWA算法的全局搜索和局部开发能力[12]。2021年，Mohammad等将维度学习搜索策略(Dimensional learning high，DLH)引入传统灰狼算法，提高了算法的全局搜索能力和标准测试函数的寻优精度[13]。这些对GWO算法的优化均未考虑灰狼个体经验对灰狼位置更新的影响以及算法后期种群多样性丧失的问题,会导致GWO算法局部开发能力差、过早收敛和收敛精度低等问题。针对这些问题，本文从四个方面优化了传统的GWO算法，这里称之为优化的灰狼算法(Optimized grey wolf agorithm, OGWA)。第一，利用Cat映射和反向学习初始化种群，增加初始种群的多样性；第二，在灰狼位置更新公式中引入粒子群算法(Particle swarm optimization,PSO)的个体经验公式，避免算法提前收敛停滞；第三，用非线性控制参数替换传统灰狼算法的线性控制参数，使收敛因子在算法前期缓慢递减，在后期迅速递减，改善了算法的搜索能力和开发能力；第四，利用Levy飞行理论对α狼进行全局搜索，维持算法后期种群的多样性，降低算法后期陷入局部最优的风险。通过与GWA算法、PSO算法和蚁群算法(Ant colony optimization,ACO)的仿真比较发现，LIGWA算法具有较高的求解精度和良好的稳定性。

1 传统灰狼算法

GWA算法是一种通过模拟灰狼群体等级制度和狩猎行为来实现参数寻优的算法。GWA算法中将灰狼群体分为四个社会等级：第一等级是灰狼群体的领导者，称为α狼，负责对狼群的狩猎对象、栖息地选择等决策;第二等级称为β狼，负责协助α狼管理群体;第三等级称为δ狼，主要负责侦察和狩猎等工作；第四等级称为ω狼，社会地位最低，需要服从前三个等级狼的领导。

(1)

(2)

(3)

式中：Rand1和Rand2表示[0,1]间的随机数；a为线性控制参数，其值随着迭代次数的增大线性递减，计算如式(4)所示：

(4)

式中tmax为最大迭代次数。

在灰狼狩猎过程中，当种群搜索到猎物位置时，α狼、β狼和δ狼距离猎物位置最近，因此，可以依据α狼、β狼和δ狼的位置Xα、Xβ和Xδ计算灰狼向猎物移动的位置，具体如式(5)～式(8)所示。

首先由式(5)～式(7)计算出其余灰狼的移动方向。

(5)

(6)

(7)

然后由式(8)更新灰狼的位置：

(8)

2 优化的灰狼算法

2.1 Cat混沌映射和反向学习相结合的种群初始化策略

2015年，刘建军等采用混沌映射初始化种群，可以增加初始种群的均匀性；2019年，张新明等在种群初始化的过程中引入反向学习理论可以增加初始种群的多样性[14-15]。本文将Cat混沌映射和反向学习两种方法相结合对种群进行初始化，提高初始种群的多样性和均匀性。Cat混沌映射具有较好的遍历均匀性，可以使初始种群均匀分布，Cat映射的数学描述如式(9)所示[16]:

(9)

利用Cat混沌映射和反向学习初始化种群,首先,要利用Cat混沌映射产生N×D维初始解矩阵C，这里N代表种群规模，D代表维度。然后，利用反向学习理论为C中的每个初始解产生与之对应的反向解，得到反向解矩阵O，计算公式为：

(10)

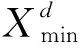
最后对初始解矩阵C和反向解矩阵O合并，得到2N×D维解矩阵J，对J中D个列向量的元素从小到大进行排序，选取每一个列向量中较小的前N个元素作为初始解，组成N×D维的优良种群矩阵。

2.2 引入粒子群个体位置更新策略

在灰狼狩猎的过程中，从式(5)～式(8)可以看出，灰狼的位置主要是根据α狼、β狼和δ狼的位置Xα、Xβ和Xδ进行更新的，在位置更新中忽略了灰狼个体经验，容易导致算法过早收敛[17-18]。相比较而言，PSO算法在位置更新方面有不容易过早收敛的优势。在优化的灰狼算法中，利用PSO算法中更新粒子个体位置信息的方法更新灰狼个体的位置信息，灰狼位置更新式(8)可以写成式(11)：

(11)

式中，灰狼个体位置更新公式：

vdi(+1)=w·(vdi(t)+G1·Rand3·(Xdi,α-Xdi(t))+G2·Rand4·(Xdi,β-Xdi(t))+G3·Rand5·(Xdi,δ-Xdi(t)))

(12)

G=2×Rand

(13)

2.3 非线性控制参数策略

(14)

式中：t为当前的迭代次数；tmax为最大迭代次数。

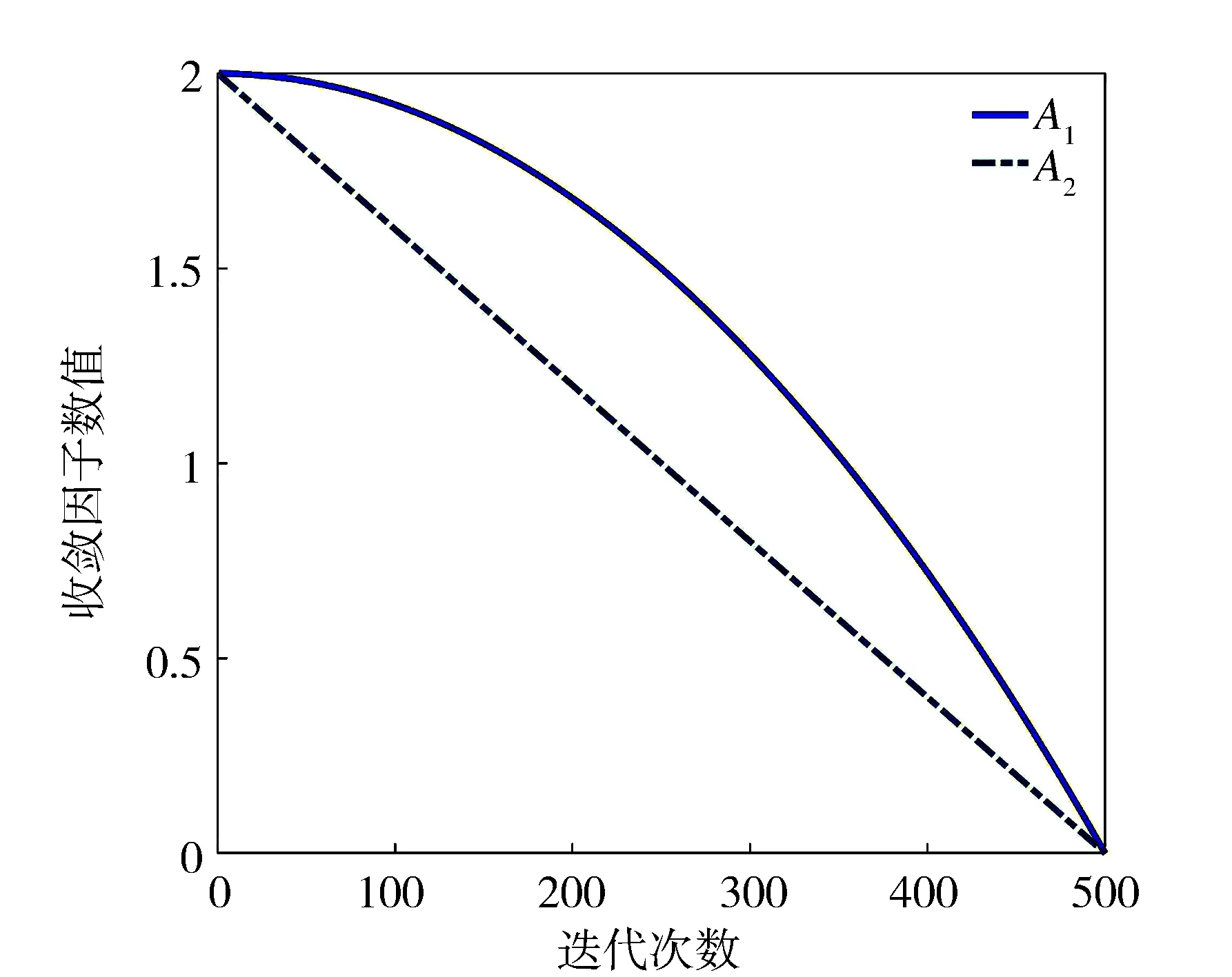
图1 收敛因子的变化曲线

2.4 引入Levy飞行更新α狼位置

在GWA算法中，α狼的位置代表最优解。在搜寻猎物的过程中，所有的灰狼均向α狼靠近，这会导致种群在迭代过程中逐渐失去多样性，使算法过早收敛[22]。针对这一不足，利用Levy飞行对α狼进行位置更新，α狼位置更新公式为：

(15)

b=Random(size(αposion))

(16)

(17)

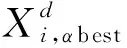
(18)

(19)

式中σu和σv分别由式(20)和式(21)计算:

(20)

σv=1

(21)

2.5 LIGWA算法步骤

综上所述，优化灰狼算法(LIGWA)的实现步骤如下：

Step1: 设置种群规模N、个体学习参数G1、G2、G3、δ和tmax。

Step2: 利用上面所述Cat映射和反向学习产生初始种群Xi，i=1,2,…,N。

Step3: 计算种群中灰狼个体的适应度值并从小到大排序，将适应度值最小的灰狼位置作为历史最优解Xα，适应度值第二小的灰狼位置作为第二最优解Xβ，适应度值第三小的灰狼位置作为第三最优解Xδ。

Step4: 利用式(15)～式(21)对α狼进行全局搜索，更新α狼的位置。

Step5: 利用式(14)计算非线性控制参数a*，按照式(2)更新收敛因子。

Step6: 对除Step 3中确定的α狼、β狼和δ狼之外的灰狼个体按式(5)～式(7)计算灰狼移动方向。

Step7: 利用式(11)更新灰狼位置。

Step8: 判断算法当前的迭代次数是否达到最大迭代次数tmax，若满足，则输出α狼的适应度值，否则返回执行Step 3重新计算适应度值，更新Xα、Xβ和Xδ。

3 仿真实验与分析

3.1 标准测试函数

为了测试LIGWA算法的性能，选取6个标准测试函数进行仿真实验，函数的表达式如表1所示。其中f1～f3为单峰函数，用来检验算法的寻优精度；f4～f6为连续多峰函数，用来检验算法后期的局部开发能力。

表1 标准测试函数

3.2 与GWA算法的比较分析

利用LIGWA算法和GWA算法分别对表1的函数进行求解。仿真实验中两种算法的狼群规模均为N=30，tmax=1 000。两种算法分别独立运行30次，求解函数的最优值、最差值、平均值和标准差。最优值代表算法求解函数得到的最小值，最差值代表算法求解函数得到的最大值，平均值代表算法的求解精度，标准差代表算法的稳定性。仿真实验结果如表2所示，函数收敛曲线如图2～图7所示。

表2 LIGWA算法和GWA算法的仿真实验结果对比

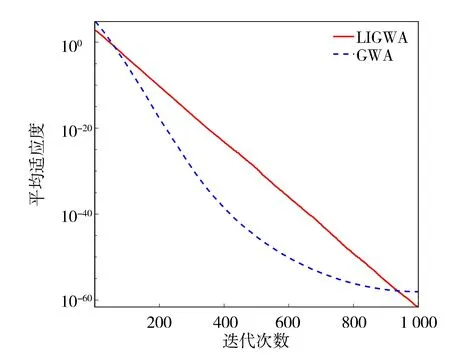
图2 函数f1的收敛曲线

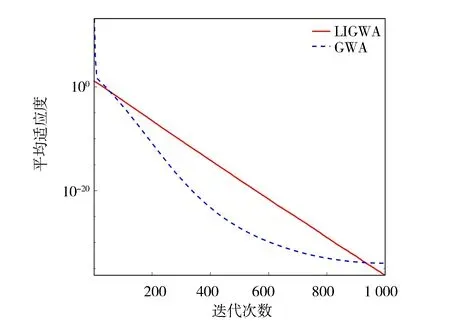
图3 函数f2的收敛曲线

图4 函数f3的收敛曲线

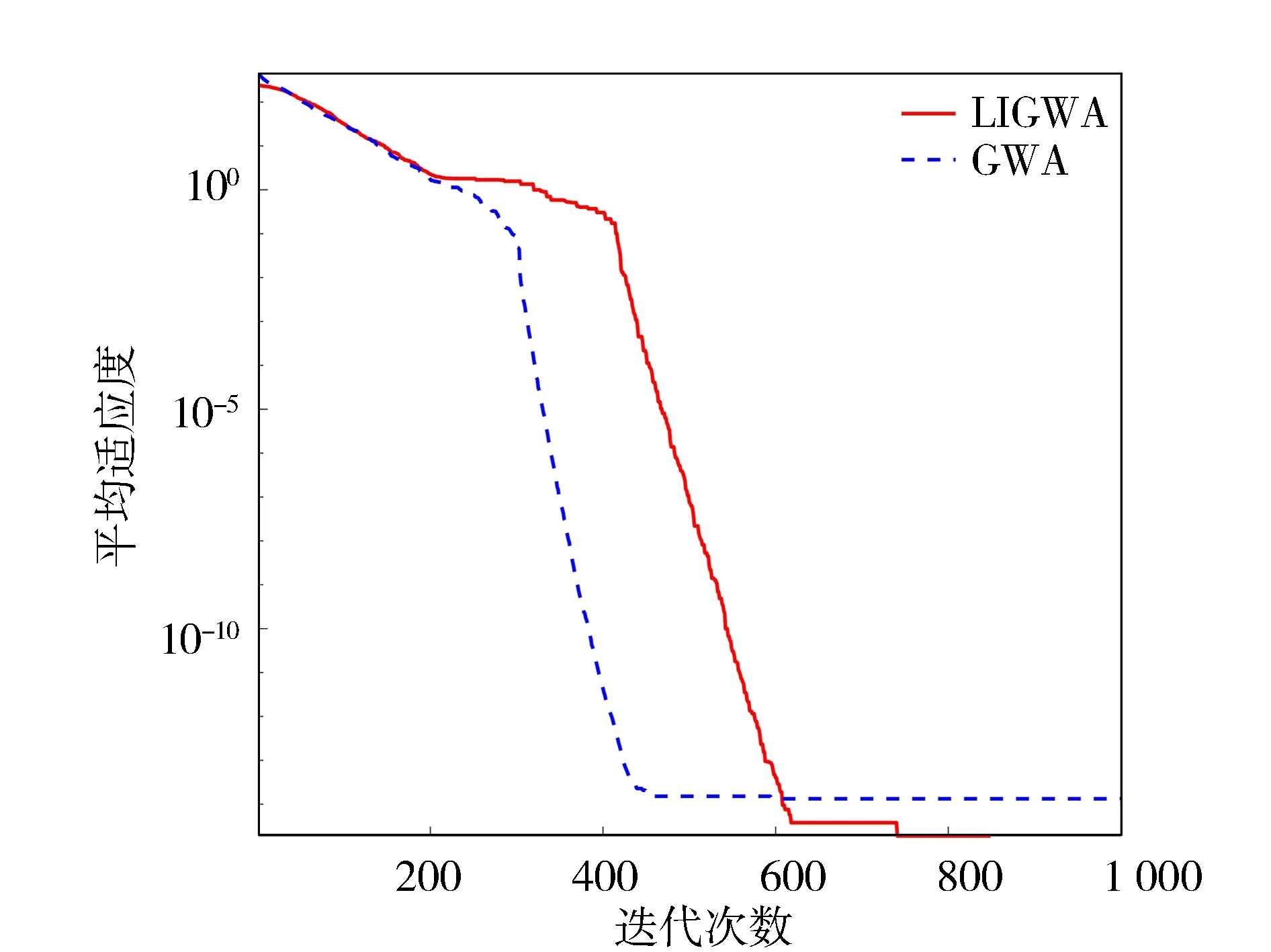
图5 函数f4的收敛曲线

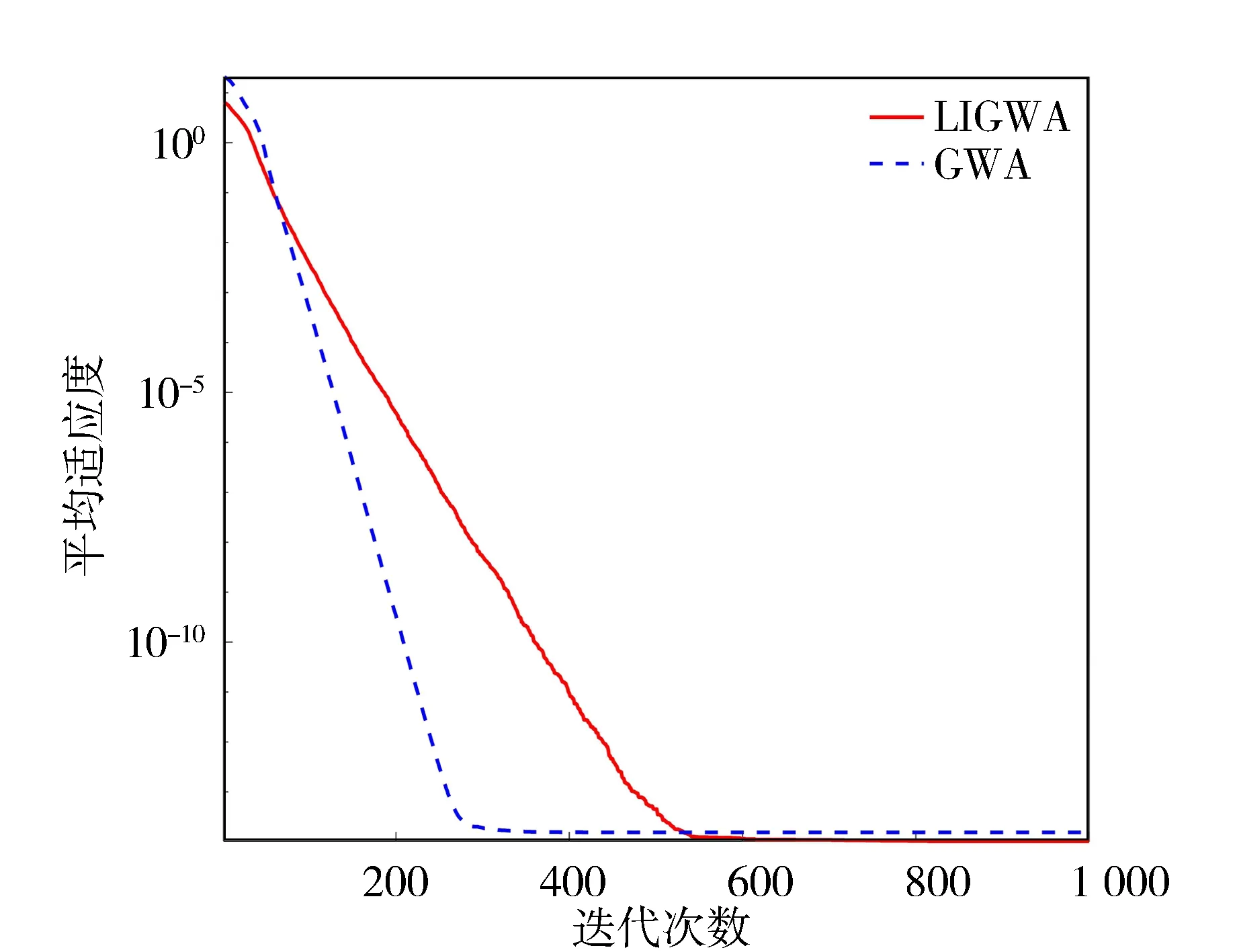
图6 函数f5的收敛曲线

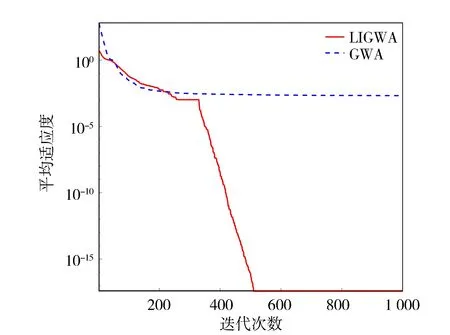
图7 函数f6的收敛曲线

从表2中的对比结果可知， LIGWA算法在6个标准测试函数上的求解精度均优于GWA算法，其中在函数f6的计算上，LIGWA算法的求解精度高出了GWA算法大约1 015个数量级，说明LIGWA算法能有效地提高全局搜索能力，降低算法后期陷入局部最优的风险。LIGWA算法在函数f1～f4、f6上的标准差小于GWA算法，而在函数f5上的标准差比GWA高出1个数量级，表明LIGWA算法在大部分测试函数上具有较好的稳定性。

由图2～图4可以看出，LIGWA算法的求解精度明显高于GWA算法，说明LIGWA算法能有效地提高算法前期的全局搜索能力和函数求解精度。由图5～图7中可以看出，GWA算法在种群迭代到500代之前就已经收敛，而LIGWA算法在迭代到500代之后才开始收敛，说明LIGWA算法能够提高局部开发能力，改善了GWA算法后期容易陷入局部最优和GWA算法收敛早熟的缺陷。由图2～图7也可以看出，相比于GWA算法，LIGWA算法的收敛速度较慢，这是由于LIGWA算法在灰狼位置更新过程中考虑了灰狼个体经验对位置更新的影响，灰狼位置更新公式变得复杂，增加了计算时长。所以，LIGWA算法是以牺牲收敛速度来提高函数求解精度以及平衡全局搜索和局部开发能力的。

3.3 与其他算法的比较分析

为进一步测试LIGWA算法的性能，将其与PSA算法和ACA算法进行对比分析，实验结果如表3所示，其中PSO算法和ACO算法的仿真实验结果来源于徐辰华等数据[23]。

表3 不同算法的仿真实验结果对比

从表3可以看出，在单峰函数和多峰函数的求解精度上，LIGWA算法的求解精度明显优于PSO算法和ACO算法，其中在函数f4的求解上，LIGWA算法的求解精度达到了函数最小值0；在算法稳定性上，LIGWA算法在函数f1～f6的标准差均小于PSO算法和ACA算法，其中LIGWA算法在函数f4上的标准差达到了0，证明本文提出的LIGWA算法是可行的。

4 结 论

为了解决传统灰狼算法存在局部开发能力弱、早熟收敛和初始种群分布不均匀等问题，提出了一种优化的灰狼算法。通过求解6个标准测试函数并与GWA算法、PSO算法和ACO算法进行对比，证明了优化灰狼算法具有较高的求解精度，改善了GWA算法早熟收敛的缺点，提高了GWA算法后期的局部开发能力，能够有效地处理单峰和连续多峰函数的寻优问题，解决神经网络、支持向量机和极限学习机等机器学习算法中目标函数的优化问题。