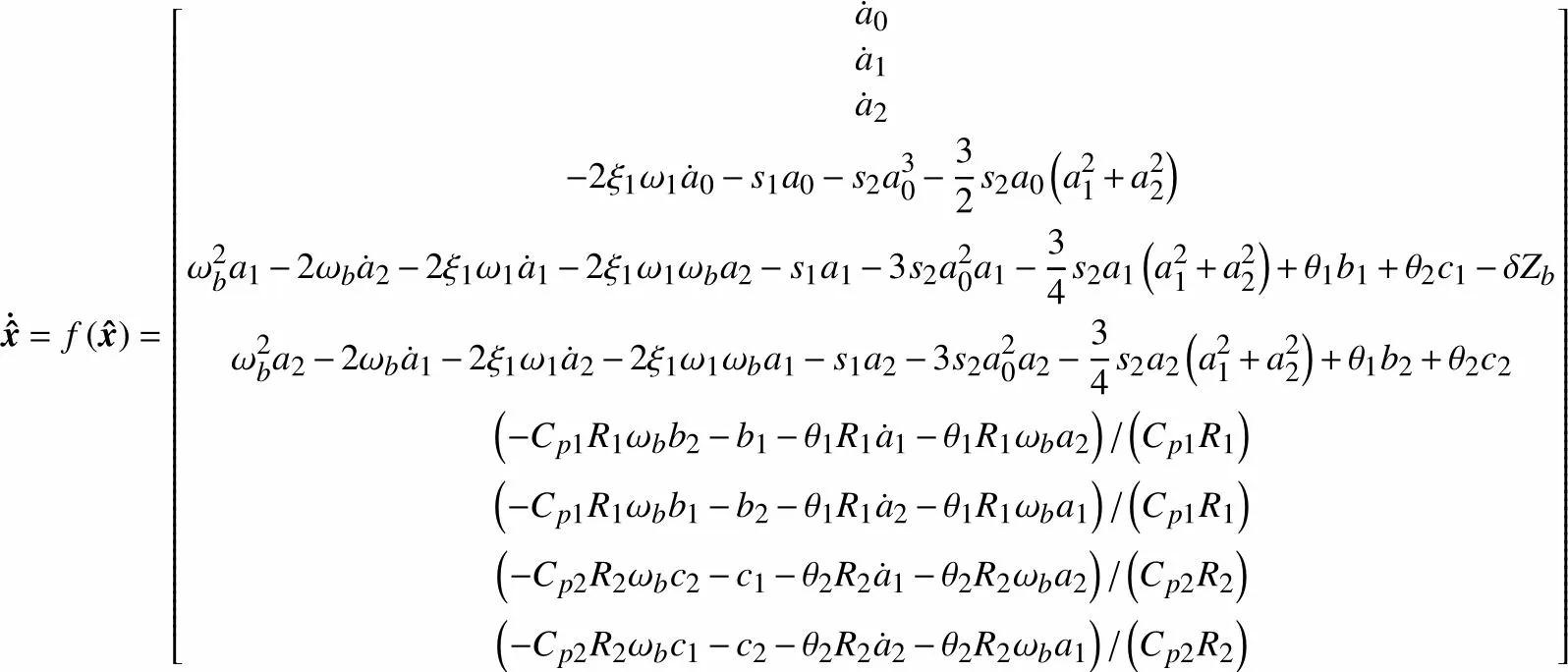磁耦合式双稳态宽频压电俘能器的设计和俘能特性1)

张伟 刘 爽 毛佳佳,2) 黎绍佳 曹东兴

* (北京工业大学材料与制造学部,机械结构非线性振动与强度北京市重点实验室,北京 100124)

† (香港理工大学土木及环境工程学系,香港九龙 999077)

引言

随着微机电系统、自供电无线传感网络、低功耗电子设备以及物联网的快速发展,振动能量俘获技术近年来受到了广泛关注,已经成功应用在航空航天工程、机械工程、生物医学工程以及众多可持续能源工程等领域中[1-3].根据俘能器对振动能量的不同转换机制,振动俘能器可以分为静电式[4]、电磁式[5]、压电式[6-7]、磁致伸缩式[8]、摩擦起电式[9-10]等.由于结构简单、便于组装,并且具有较高的能量转换率,压电式、磁电式以及压电-磁电耦合的振动俘能器的动力学行为及其俘能特性已成为国内外研究的热点之一.

传统的线性振动俘能器的工作效率过于依赖自身的共振频率,微小的制备误差便可能导致系统的输出功率急剧下降[11];并且,传统的振动俘能器工作频带过窄,无法与环境中随机、宽频的振动频率匹配,导致不能实现预期的俘能效果[2].为了提高振动能量俘获系统的效率和实用性,急需设计能够与环境振动特征相匹配的振动能量俘获结构[1],实现低频宽带的俘能效果.

非线性系统复杂的动力学行为[12-15]为拓宽振动俘能器的工作频带,提高振动俘能器的效率提供了新思路,越来越多的学者将具有非线性刚度[16-18]特征的结构引入振动俘能器中,形成具有非线性单稳态和双稳态特性的振动俘能器[5,19-21],使系统的共振频率发生偏移,拓宽其工作带宽.Ramlan等[22]和Liu 和Jing[23]分别在单稳态系统中引入了非线性刚度弹簧和X 型支撑结构.Chen等[24]利用非线性磁力构造了存在内共振的压电梁俘能器结构,在更宽的频带范围内实现了更大幅度的振动响应.Zhu等[25]和Masana 和Daqaq等[26]利用结构的几何非线性,结合压电梁的屈曲设计了具有双稳态特性的压电俘能器.Li等[27]通过引入非线性磁力研究了磁力双稳态压电陶瓷悬臂梁的俘能特性和动力学行为.这些研究均表明,系统的双稳态非线性跳跃机制能够显著拓宽系统的频响范围,增大俘能器的有效频带宽度[28-29].

由于环境动载荷存在多方向性、多变性以及多样性,设计与实际环境相匹配的高性能振动能量俘获系统显得尤为重要[30-31].目前较多的研究都集中在发展多方向振动能量俘获动力学,包括两个方向[32-33]、三个方向[34]、平面内任意方向[35-36]以及空间中任意方向[37]的振动能量俘获系统.值得注意的是,这些结构一旦被设计出来,其工作频率往往都是固定的,无法根据环境中的振动而发生相应的变化.本文通过引入可移动铰支座和非线性磁力,实现一类具有可变频率特征的磁耦合式双稳态压电俘能器,实现了低频宽带的俘能效果.

本文首先在带有活动铰支座的简支梁一侧添加一对永久磁铁,并将其简化为欧拉-伯努力梁,利用拉格朗日方程建立系统的非线性动力学方程,分析系统的可变频性;然后利用谐波平衡法对动力学方程进行求解,并研究系统参数、磁间距、负载阻抗、外激励频率和幅值等对系统双稳态以及俘能特性的影响,从而保证系统的低频宽带俘能效果,并进行了实验验证.

1 结构模型和基本假设

如图1 所示,带固定永磁铁α的压电梁,总长度为L,建立(x,z)坐标系,梁一侧x=0 为固定铰支座约束,另一侧为活动铰支座约束,活动铰支座能够发生纵向位移L1∈(0,L],但无横向位移.固定永磁铁α与固定永磁铁β之间的距离为D,两磁铁的长度分别为Lα和Lβ,宽度为Bα和Bβ,厚度为Hα和Hβ.梁基础层厚度为H,在基础层的上下两侧分别铺设厚度为Hp的压电陶瓷,形成压电双晶片的串联构型.

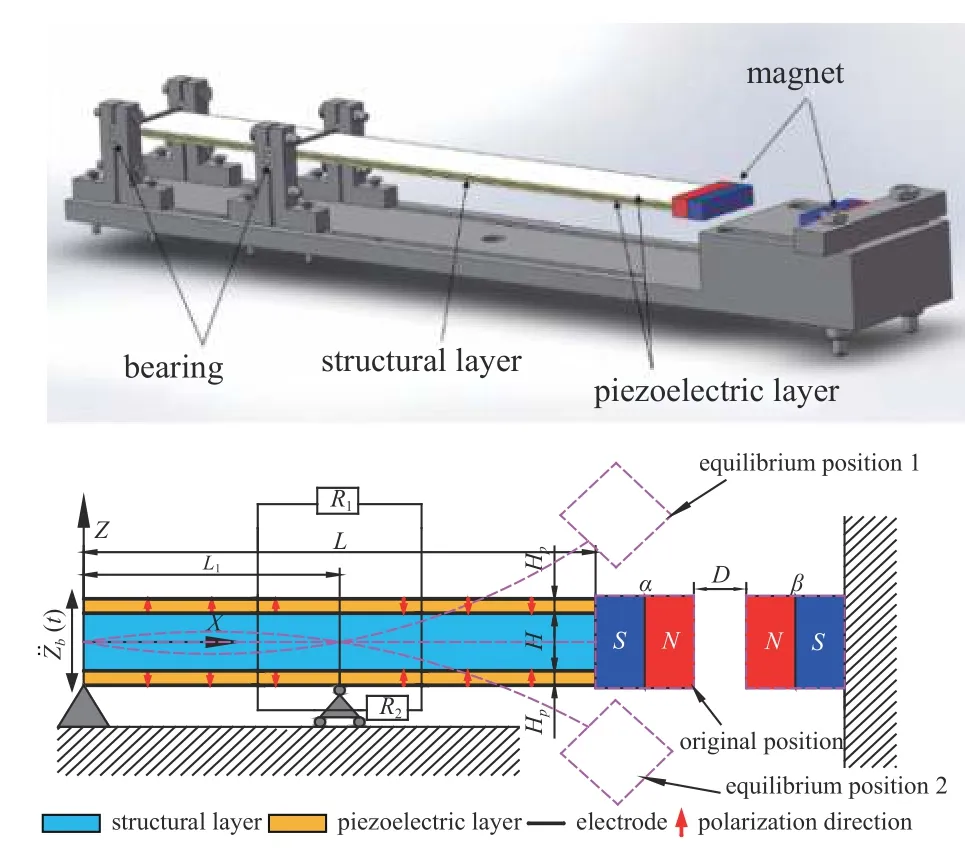
图1 磁耦合式双稳态宽频压电俘能器模型Fig.1 Model of piezoelectric energy harvester with magnetically coupled bistable wide-band

结构受到竖向简谐加速度激励(t) 作用,考虑基本假设:(1)压电梁为欧拉-伯努力梁,只发生横向振动;(2)压电层和基础层均为各向同性材料,且压电层和基础层之间为理想粘结;(3)压电层中瞬时感应电场的场强在其总长度上是均匀分布的;(4)不考虑永磁铁的变形,但考虑其转动惯量;(5)磁偶极子模型[38]适用.

2 理论模型的建立

2.1 分布参数多场耦合能量函数的描述

基于假设(1),压电外伸梁的轴向应变S1

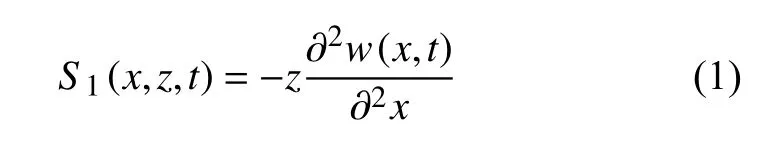
式中w(x,t) 为梁的横向位移.

基础层和压电层的本构关系分别为

式中,vR1(t) 为负载阻抗R1两 端的电压,vR2(t) 为负载阻抗R2两端的电压.

系统的拉格朗日函数 ℓ (x,t) 为

式中,T,U,We和Um分别为系统的动能、内势能、电势能和磁势能

基于假设(5),系统的磁力势能可表示为[38]

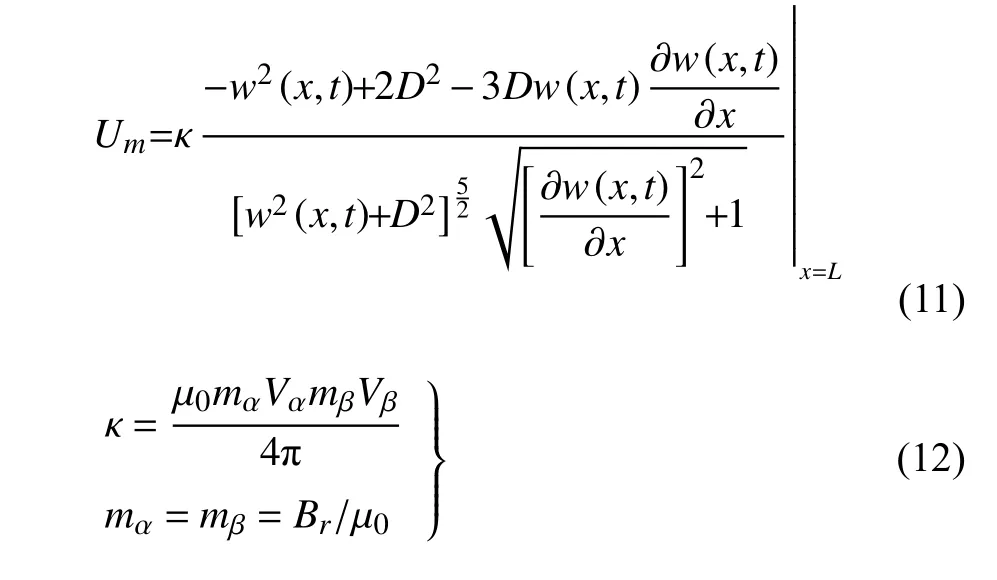
式中,下角标“b”,“p”和“ α ”分别表示基础层、压电层和永磁铁 α ;ρ,A,M,m,J和I分别表示质量密度、横截面面积、质量、磁化强度、转动惯量和惯性矩;B为基础梁的厚度;V为永磁铁的体积;µ0为真空磁导率;Br为磁铁的剩余磁通量密度[38].

2.2 压电俘能器动力学方程的建立

压电外伸梁的横向位移w(x,t) 可以表示为

式中,Wi(x) 为第i阶模态振型,qi(t) 为广义模态坐标.为实现模态解耦,并保证振型惟一性,进一步将模态振型标准化,引入下述正交条件

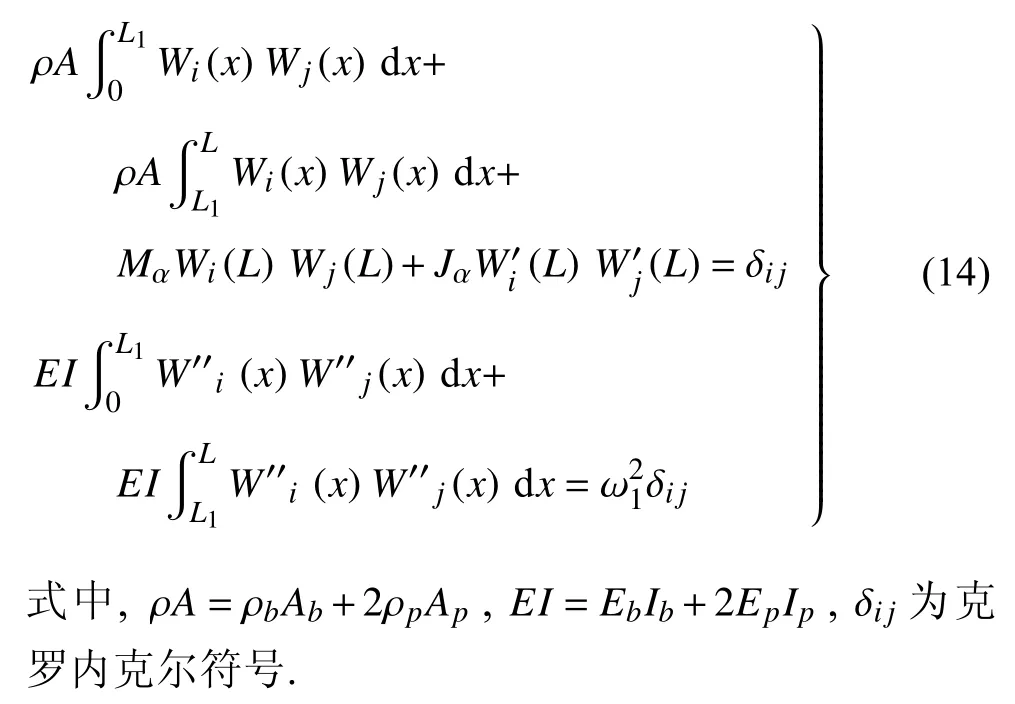
一般来讲,压电俘能器的一阶固有频率在结构的位移响应中发挥主导作用[38],引入伽辽金一阶截断对位移函数w进行求解

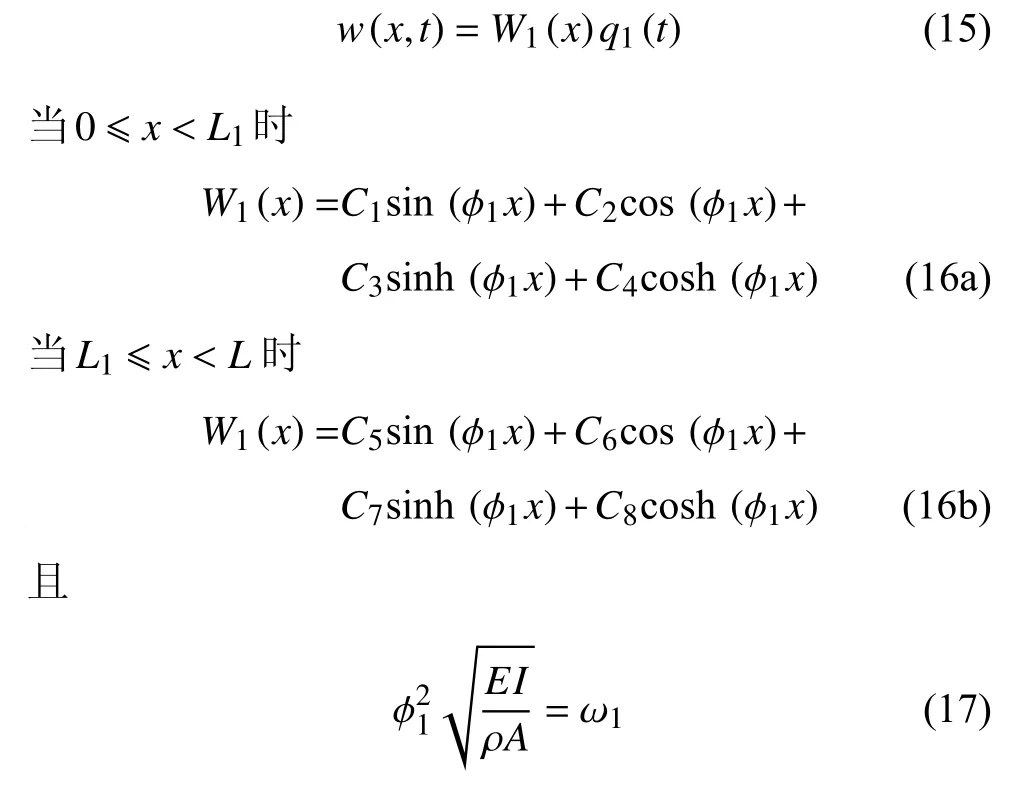
由于C1,C2,···,C8必须满足边界条件,有

其中,ζ=(C1,C2,···,C8)T,A为系数矩阵.通过求解式(19)得到系统的一阶固有频率 ω1及其振型函数W1(x).

将式(15)代入式(11),并进行泰勒级数展开,有

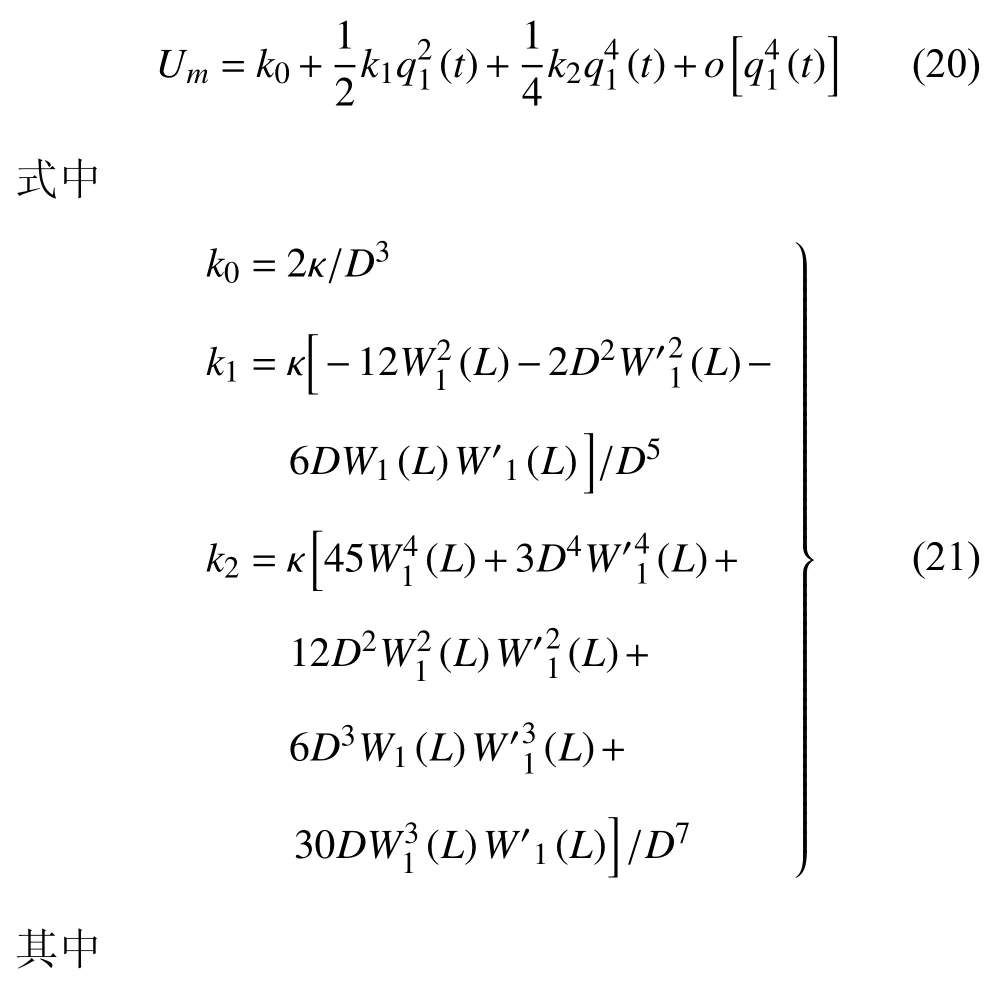
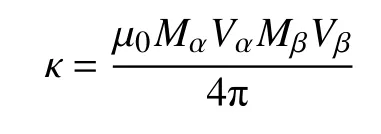
将式(15)代入式(6)、式(8)、式(10),结合式(13)和式(19)计算拉格朗日函数式(5),代入拉格朗日方程有

3 动力学方程的求解

3.1 谐波平衡分析

假设式(23)的稳态解为

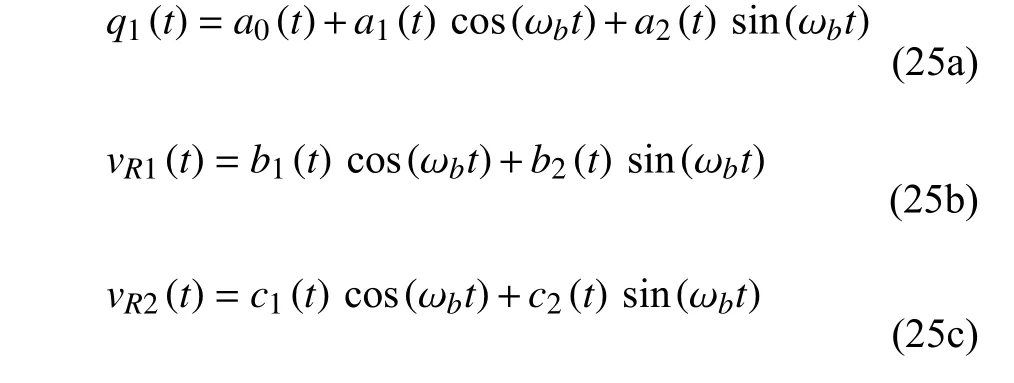
式中,a0(t) 表示系统的平衡位置.将式(25) 代入式(23),令方程两边的常数项、含有 s in(ωbt) 以及含有 c os(ωbt) 的系数分别相等,忽略高次谐波项,得到

3.2 稳定性分析

4 数值分析

基础层、压电层和磁铁分别选用铍青铜、压电陶瓷PZT-5H 和钕铁硼,表1 给出了具体的材料参数和几何参数[20].

表1 系统的几何参数和材料参数[20]Table 1 Geometric and material parameters of the system[20]

图2 给出了系统的线性刚度s1和非线性刚度s2随磁铁间距D以及长度比变化的曲线.如图所示,系统线性刚度s1对磁铁间距D和外伸长度比ε=L1/(L-L1)的改变均非常敏感,即调节长度比和磁铁间距能够实现结构的可变频性,而系统非线性刚度s2只对磁铁间距D的变化较为敏感.随着磁铁间距D的减小,即非线性磁力的增大,系统开始出现非线性刚度s2,线性刚度s1从正值变为负值,系统从单稳态变为双稳态.并且,系统进入双稳态所需的磁铁间距D随着长度比 ε 的增大而减小.

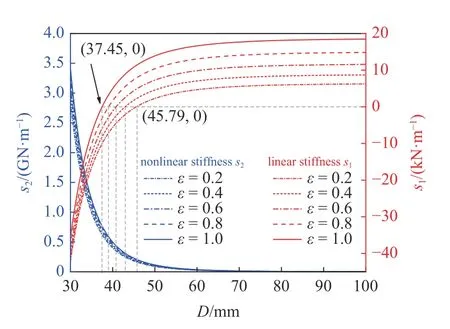
图2 磁铁间距和长度比对系统刚度的影响Fig.2 Effects of magnet spacing and length ratio on stiffness

图3 给出了磁铁间距D=30 mm,35 mm,40 mm,100 mm)与系统双稳态特性之间的关系,其中弹性势能UE=Ub+Ups、总势能、Um为磁势能.当总势能Ut出现两个势阱和一个势垒,系统存在两个稳定的平衡点和一个不稳定的平衡点,即系统表现为双稳态特性.随着D的增大,系统的磁势能减小,两势阱间的深度降低,直至势垒消失.随着长度比 ε 的增大,两势阱间的深度也降低,系统的双稳态特性更容易实现.

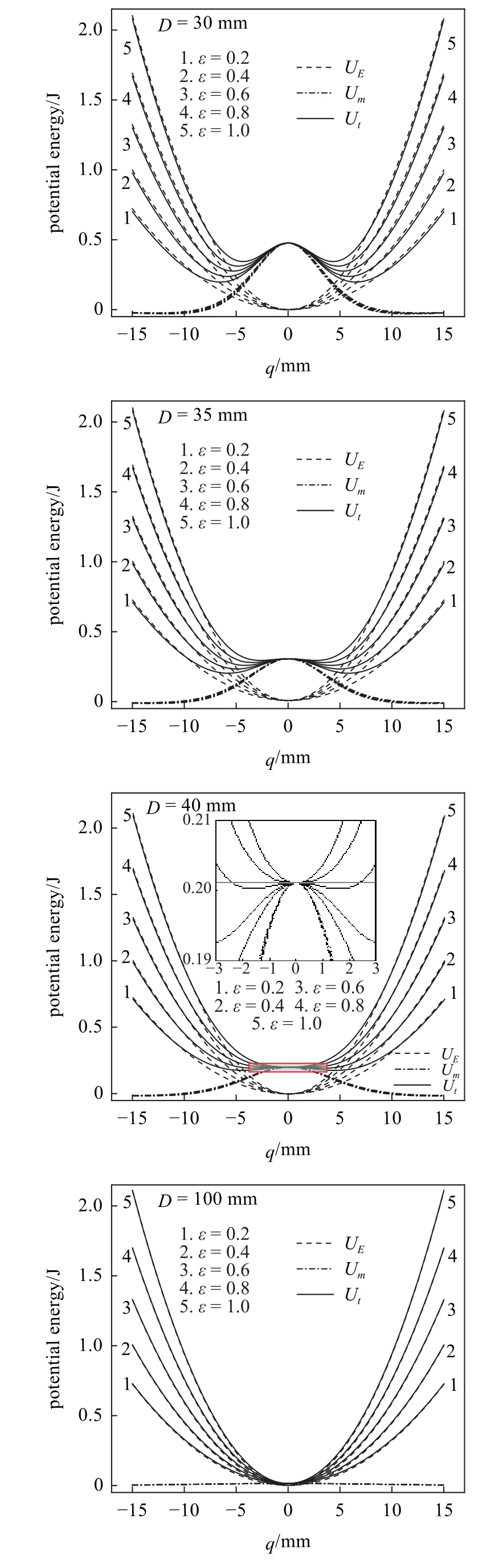
图3 系统的势能曲线Fig.3 Potential energy curves of the system

为了研究加速度激励幅值Zb、激励频率f、长度比 ε 以及负载阻抗R1=R2=R等参数对系统俘能特性和动力学行为的影响,在后续的分析中磁铁间距均取为D=35 mm,即系统在各长度比下的线性刚度均为负值,在外激励的作用下,系统呈现双稳态特性,出现大幅阱间运动和小幅阱内运动,进而增大系统的俘能效率.

当Zb=1 m/s2时,图4 给出了加速度激励频率f和长度比 ε 对压电俘能器的位移频响曲线(a)和输出功率(b)的影响.实线表示系统的稳定响应,虚线表示不稳定响应.在低频段(0 Hz 附近),大幅阱间运动引起较大的输出功率,尤其是长度比 ε 较小的系统.在式(28)中注意到,系统的输出功率不仅与系统振幅 η 有关,还与节点处转角相关系数 θ1和 θ2有关.由于 长度比 ε=0.6 的 转角相关系数大于 ε=0.4 的转角相关系数,在低频范围内,长度比 ε=0.6 的系统具有较高的输出频率.同时,随着外激励频率的增大,较大长度比(ε=0.8 和 ε=1.0)系统以阱内运动为主,较小的长度比(ε=0.2,0.4,0.6)系统以阱间运动为主,因此,在较高频率范围内,ε=0.2,0.4,0.6 具有较高的输出功率.

图4 外激励频率和长度比对(a)振幅和(b)输出功率的影响Fig.4 Effects of frequency and length ratio on (a) vibration amplitude and (b) output power

从以上的分析可知,系统总存在一个长度比使得系统输出功率达到最大,实现压电俘能器低频宽带的俘能特性.图5 给出了系统的工作频带以及对应的输出功率.针对不同的环境振动频率,给出了较为合适的长度比,以及对应的输出功率.图中不同颜色表示不同的长度比,可以通过调节结构中可移动铰支座的位置来实现,从而保证在环境变化过程中,获得最高的输出功率.

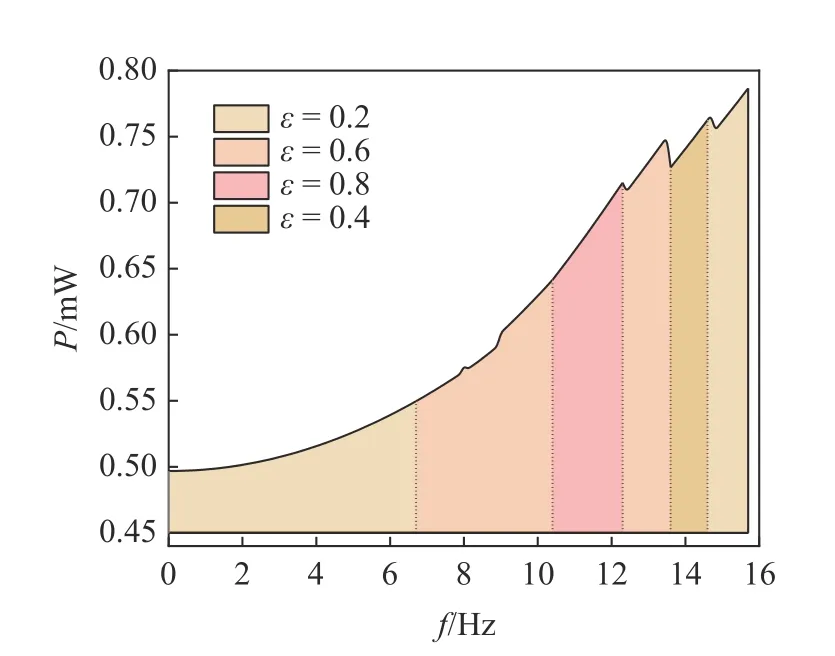
图5 工作带宽及对应的输出功率Fig.5 Working frequency band and corresponding output power

当ε=0.2和Zb=1 m/s2时,图6给出了激励频率f和负载阻抗R对系统阱间运动6(a)和阱内运动6(b)输出功率P的影响.当 ε=0.2 和f=4 Hz 时,图7给出了激励幅值Zb和负载阻抗R对系统阱间运动7(a)和阱内运动7(b)输出功率P的影响.由图可知,阱间运动的输出功率明显高于阱内运动;不管是阱间运动还是阱内运动,均存在最优负载阻抗Ropt.并且,系统的最优负载阻抗随着激励频率的增大而减小,对激励幅值的变化不敏感.

图6 频率和负载阻抗对输出功率的影响Fig.6 Effects of frequency and load resistance on output power

图7 激励幅值和负载阻抗对输出功率的影响Fig.7 Effects of amplitude and load resistance on output-power

图8 分析了长度比 ε 对系统最优负载阻抗Ropt的影响.如图所示,随着长度比的增大,阱间运动和阱内运动对应的最优阻抗均增大,并且阱间运动的最优阻抗大于阱内运动的最优阻抗.

图8 长度比对最优负载阻抗的影响Fig.8 Effect of length ratio on optimal load resistance

为了进一步说明R1和R2对最优负载阻抗的影响,以加速度激励z¨b=cos(8πt) 为例,图9 给出了系统阱间运动时,R1和R2对输出功率的影响.当给定R2的阻值时,系统的输出功率对横坐标R1的变化非常敏感,即能够得到一个最优的负载阻抗R1opt;当给定R1的阻值时,横坐标R2内的变化对系统的俘能特性影响并不明显,即R1对系统的最优负载阻抗的贡献较大.

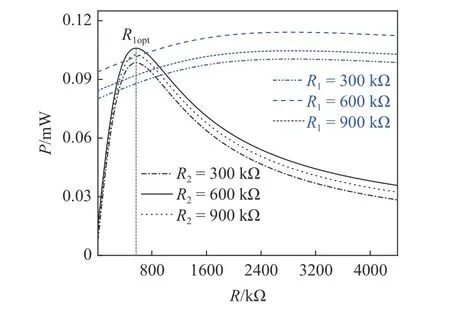
图9 不同外激励下R1和R2 对最优负载阻抗的影响Fig.9 Effects of R1 and R2 on optimal load resistance under different external excitation

5 实验验证

为了说明本文的正确性,利用图10 所示的磁耦合式双稳态宽频压电俘能器实体模型和实验设备对系统的振动特性和俘能效果进行了验证.

图10 实验设备Fig.10 Experimental equipment

图11(a) 对比了相同加速度激励z¨b=cos(28πt)作用下,长度比ε=0.2和ε=0.4系统振动特性的理论和实验结果.在不同外激励频率下,图11(b)对比验证了不同长度比下系统的输出电压和输出功率.由图可知,关于系统的振动特性,实验与理论结果吻合较好,而系统的输出电压和输出功率出现误差,分别在10%和20%左右.输出电压的误差主要来源于压电材料在制备过程中,其压电系数无法与理论值完全一致.并且导线和实验仪器均存在内阻,系统的输出功率对电阻的变化较为敏感,导致系统输出功率的误差较大.因此,本文设计的磁耦合式宽频压电俘能器的正确性和有效性得到了验证.

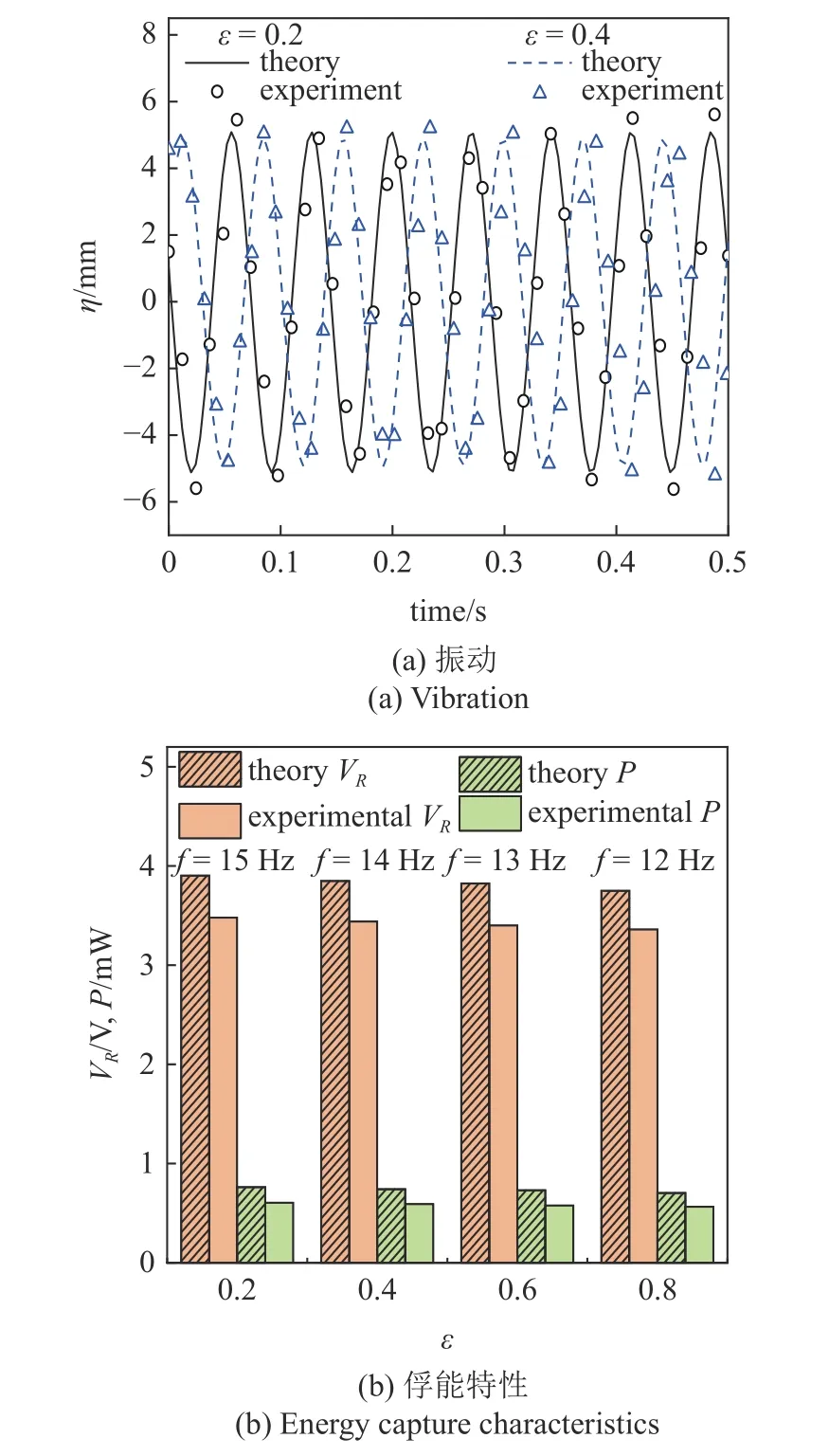
图11 振动和俘能特性的实验验证Fig.11 Experimental verifications of vibration and energy capture characteristics

6 结论

本文提出了一种具有双稳态特性的磁耦合式宽频压电俘能器,通过建立其非线性动力学模型,分析并讨论了不同参数对系统俘能特性的影响,并对结果进行了实验验证,主要结论如下:

(1)非线性磁力的引入使系统出现负刚度,呈现双稳态特性,实现超低频环境下的俘能需求;

(2) 通过调节可移动铰支座的位置,实现系统的可变频性,匹配环境中随机、宽频的振动特性;

(3) 随着长度比的增大,系统进入双稳态所需的磁铁间距变小;

(4) 系统最优阻抗对外激励频率和长度比的变化较为敏感,对外激励幅值的变化不敏感.

附录

式(26)可改写为非线性自治系统的形式