黏性阻尼系统时域响应灵敏度及其一致性研究1)

张磊 张 严 丁 喆

(武汉科技大学冶金装备及其控制教育部重点实验室,武汉 430081)

(武汉科技大学机械传动与制造工程湖北省重点实验室,武汉 430081)

引言

灵敏度分析用于定量预测结构参数变化对系统响应或模型的影响,在模型修正[1-2]、拓扑优化[3-6]、损伤识别[7]、可靠性分析[8]等研究工作中具有重要意义.工程结构在实际服役时不可避免的受到复杂外界环境的振动或冲击影响,往往要求进行时域动态响应的分析,且经常会伴随着噪声以及结构系统自身的振动,这都对结构动力设计及优化问题造成了困难.因此开发出高效准确的时域响应灵敏度分析方法非常必要.根据计算方式不同,灵敏度计算方法可主要分为[9]:有限差分法、直接微分法和伴随变量法.有限差分法是一种直接而简单的方法,但是计算效率较低,通常作为衡量灵敏度求解方法精度的参考解.已有的研究表明[10],当设计变量数目大于有效约束数目时,伴随变量法比直接微分法计算效率更高.

动力响应的灵敏度求解对结构动态性能的分析及优化非常重要.目前为止,众多学者已经对该领域进行了广泛的研究.Choi等[11]在波导滤波器的优化设计中,利用增广拉格朗日法、材料导数概念和伴随变量法,系统的推导了频域解析灵敏度公式.周大为等[12]针对黏性阻尼系统的频响振幅灵敏度求解问题,并结合广义模态截断扩增方法,提出了一种具有更高精度的伴随变量法.Zhao等[13]提出了一种自适应混合展开法来确定需要计算的低阶特征频率和特征模数,然后再采用伴随变量法进行灵敏度分析,以克服简谐激励下的拓扑优化问题计算量大的困难.

上述研究讨论了伴随变量法求解频率响应灵敏度的问题.然而,实际工程由于工作环境复杂,结构系统时域响应的灵敏度分析同样非常重要.Elesin等[14]在非线性光学器件的拓扑优化结构设计中,采用了伴随变量法求解时域响应灵敏度.Mello等[15]在减少微机电系统响应时间的拓扑优化中,对于时域相关目标函数的灵敏度求解同样采用了伴随变量法.Zhao 和Wang[16]研究了涉及时域动力响应的拓扑优化问题,其中对时域响应相关的目标函数灵敏度分析采用了伴随变量法.此外,还有一些学者也采用伴随变量法来进行时域响应问题相关的灵敏度分析[17-19],用以优化结构在外载荷作用下或应力约束下的机械性能,如最小化能量耗散、动柔度和结构总体积等.时域响应灵敏度求解同时涉及设计变量的微分计算和时间域的离散化,因此微分和离散的先后顺序可能对时域响应灵敏度的计算结果产生影响.但上述研究均利用先微分后离散的伴随变量法实施.然而,Le等[20]在进行材料微观结构的拓扑优化时指出先微分后离散的伴随变量法会导致一致性问题,而采用先离散后微分的伴随变量法可大幅降低一致性误差.

一致性误差用来描述某灵敏度计算方法的结果与数值参考解间的偏差,它与计算量和实现难度被共同视为评价灵敏度算法性能的三项准则[21].Jensen等[22]指出基于Newmark 方法的先微分后离散伴随变量法会产生一致性误差,而解决此问题可用先离散后微分方法.胡智强和马海涛[23]针对伴随变量法的一致性问题进行了更为细致的研究,发现若能保证动力响应分析结果的精度,先微分后离散法的一致性误差并不会影响灵敏度结果的可靠性.Yun 和Youn[24]针对黏弹性阻尼系统,提出了一种先离散后微分的时域响应灵敏度求解方法,并将其应用于黏弹性系统微结构拓扑优化.文献[25]通过基于密度的多材料拓扑优化方法,并结合先离散后微分的伴随变量法进行灵敏度分析,提出了一种新颖的计算框架,用于在有限变形的时变载荷条件下设计最佳耗散(阻尼)超材料.文献[26]基于有限变形理论,提出了一种针对动态问题的拓扑优化方法,推导出了一种能在任意变形动载荷下减小变形的结构.并利用先离散后微分的伴随变量法建立了一个通用设计灵敏度方程,以准确地反映结构对动载荷的响应.此外,先离散后微分方法也被扩展至非黏性阻尼系统[27]和非线性系统[28].

上述方法的动力响应分析均基于Newmark 方法开展,因此伴随变量也是通过Newmark 积分方案进行求解.当时间步长较大时,Newmark 积分法可能不能精确反映某些高频振动的分量[29],进而影响求解精度;减小时间步长可提高计算精度,但会大幅增加计算时间,这也导致了基于Newmark 积分方案的伴随变量法在一定程度上限制了灵敏度算法性能.改进精细积分法(MPIM)[30]由于采用2N类算法,且载荷项用高斯-勒让德积分近似,使其在求解结构系统时域响应时能够同时保证高精度和高效率.Ding等[31]针对非黏性阻尼系统时域响应灵敏度计算问题,提出了基于MPIM 方法的先离散后微分和先微分后离散伴随变量法,并且对两种方法的计算性能进行了详细的比较.但非黏性阻尼系统时域响应灵敏度误差主要来源于卷积型阻尼模型的近似处理,与黏性阻尼系统存在本质上的区别.因此,其结论并不能直接适用于黏性阻尼系统.

综上所述,针对黏性阻尼系统时域响应灵敏度求解问题,本文推导了基于MPIM 的先微分后离散和先离散后微分两种伴随变量方法的理论表达.通过数值算例验证了两种方法的有效性和准确性,并与传统基于Newmark 的方法进行比较.讨论了微分和离散的先后顺序在不同积分方案条件下对时域响应灵敏度计算性能的影响,为黏性阻尼系统时域梯度优化算法奠定了基础.

1 问题提出

1.1 灵敏度分析的伴随变量法

对于N自由度黏性阻尼系统,其运动方程可表示为

对于时域响应优化问题,响应函数(或目标函数)通常定义为由位移、速度和加速度组成的积分形式,即

在伴随变量法中,通常引入伴随变量 λ 构造增广多项式

式中,R(t) 为一恒等于零的多项式,通常与系统运动方程相关.

1.2 灵敏度分析结果的准确性与一致性

准确性用来描述算法结果与解析解的相近程度,两者的偏差用精度表示.而一致性用来描述算法结果与数值参考解的相近程度,两者的偏差用一致性误差表示.

考虑到文章的简洁性,本节以响应函数r为例,分别以ra(t,p)和rb(t,p,Δt) 表示解析解和数值解.其中p为设计变量,t为时间,Δt为时间步长.响应函数r对p灵敏度可定义为

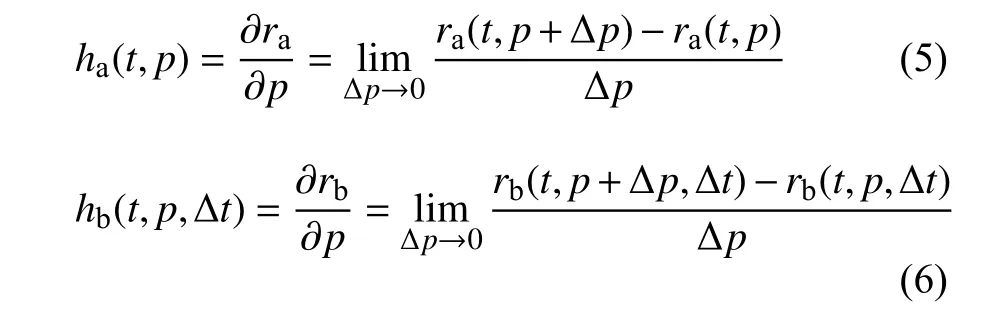
显然,响应函数的解析解ra(t,p) 与数值解rb(t,p,Δt)之间存在偏差,这是由数值解存在的时间离散误差而引起的偏差.基于此,由式(5) 和式(6)给出的灵敏度结果也会有不同.为区分灵敏度分析方法的准确性与一致性,在相同的时间离散情况下,若某种灵敏度分析方法计算出的结果为h(t,p,Δp),则可定义两种误差为

按上述理论,ε 定义为计算精度,其数值反映灵敏度分析方法的准确性;而 εc定义为一致性误差,其数值反映灵敏度分析方法结果与数值参考解偏差.由于时域逐步积分方法所得动力响应解仅能保证在离散时间点处严格满足动力平衡方程,因此先微分后离散伴随变量法在理论上会给出不一致的灵敏度求解结果,较大的一致性误差,将无法准确反映参数变化对响应函数的影响,进而造成后续计算和优化结果的严重偏差.

2 动力方程的数值解法

本节将简要介绍后续内容中涉及到的关于式(1)所表示的黏性阻尼系统动力方程的求解方法,即Newmark 方法和MPIM 方法.

2.1 求解动力响应的Newmark 逐步积分法

利用Newmark 法进行求解,其逐步积分列式为[32]

2.2 基于状态空间的MPIM法

对于黏性阻尼系统,首先将其运动方程转化为状态空间形式.引入状态空间向量

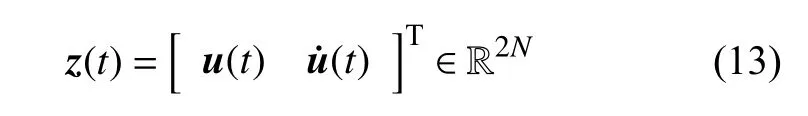
于是,式(1)转化为状态空间表达式

在式(14)中,A为状态空间矩阵,z(t) 和Q(t) 分别为状态空间中的状态向量和力向量.基于状态空间表达式,求解时域响应的MPIM 逐步积分递推公式为[22]

其中,l为高斯求积节点数,ωi和 ζi分别为高斯节点和高斯求积系数,T(Δt) 为指数矩阵函数,定义为

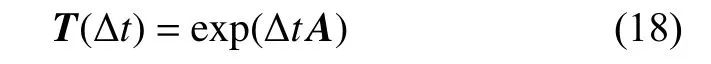
若已知运动的初始值z0,由式(17)迭代计算可得各时刻点位移、速度、加速度.当时间步长较大时,MPIM 方法的计算精度高于Newmark 方法,而当时间步长较小时,两方法虽可得到相近的结果,但前者的计算效率更高.接下来,将基于MPIM 方法,分别推导出针对黏性阻尼系统时域响应灵敏度求解的先微分后离散和先离散后微分伴随变量法.

3 基于MPIM 的先微分后离散法

式(2)表示的响应函数在状态空间内可等效的表示为

3.1 响应函数的微分

引入任意2N维伴随变量向量λT(t),定义

由于式(14)在任意时刻均成立,因此响应函数r等于恒成立.对于它们的灵敏度,同样有

令式(20)对设计变量p求微分,得

由于式(22)对任意伴随变量 λT均成立,同时为了消除上式中含时域响应偏导数的各项,可得如下关系

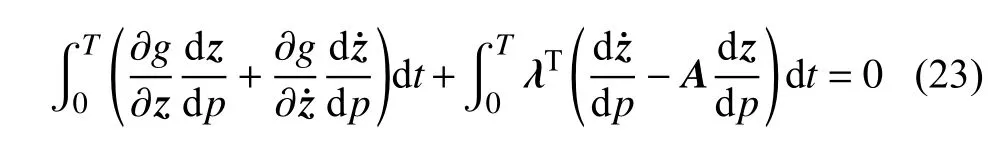
对式(23)进行分部积分,并整理得

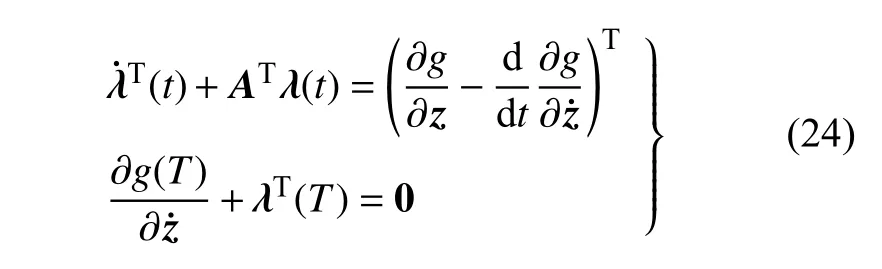
显然,式(24)为一阶常微分方程的终值问题.引入变量代换s=T-t,式(24)即等价的变为常见的一阶常微分方程初值问题,即

3.2 响应函数的离散

结合式(21)、式(22)以及式(25),响应函数r的灵敏度表达式即为

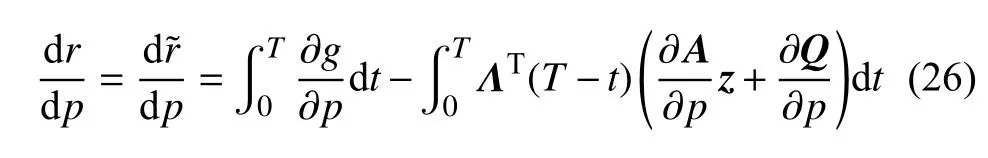
式中,动力响应z的在每个离散时间点已知,于是响应函数的灵敏度可用梯形积分公式近似表示为

可以看到,为获取响应函数的时域灵敏度,本方法先对其进行微分运算以推导出伴随方程,然后在时域内对伴随方程进行离散求解.因此该方法称为先微分后离散的伴随变量法.

4 基于MPIM 的先离散后微分法

4.1 响应函数的离散

对于先离散后微分的伴随变量法,首先将式(19) 表示的状态空间下的响应函数在各时间点nΔt(0 ≤n≤T/Δt)进行离散

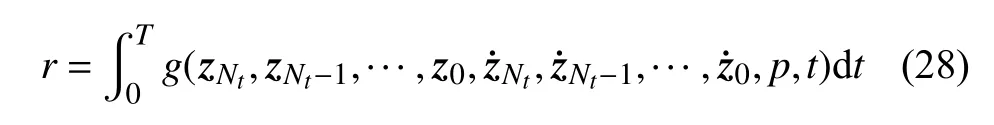
同样地,响应函数r的灵敏度可以由梯形积分公式近似求解,即

利用式(17)可定义残值多项式为

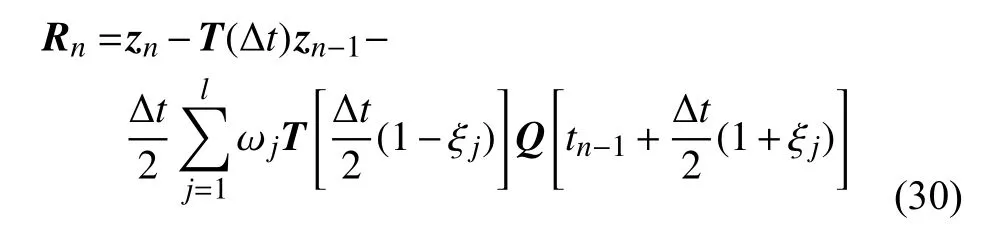
显然,式(30)在任何时刻tn严格满足Rn=0 .

4.2 响应函数的微分

引入任意2N维伴随变量向量,利用残值多项式(30)构造增广方程

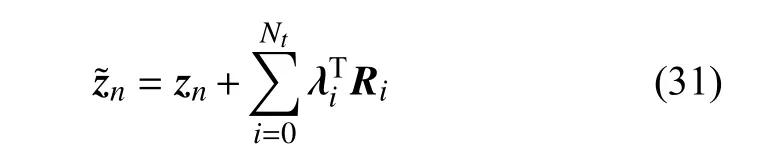
由于Ri恒等于零,因此=zn在任意时刻点也恒成立,对于灵敏度同样有

进一步有

将式(33)进一步展开并整理

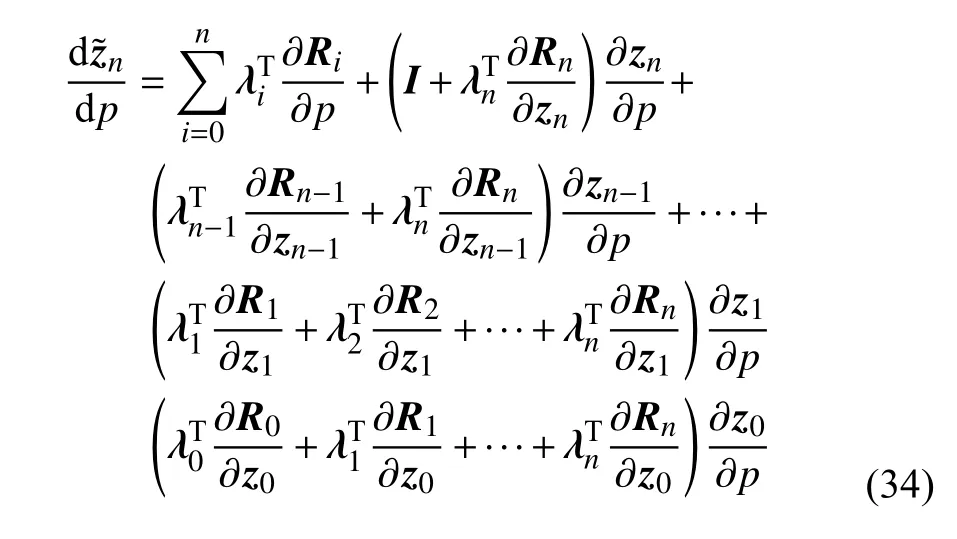
由式(30)可知,残值方程Ri对状态空间向量zi的灵敏度可表示为

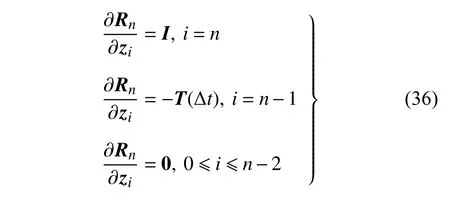
将式(36)代入式(35),可得伴随变量表达式为

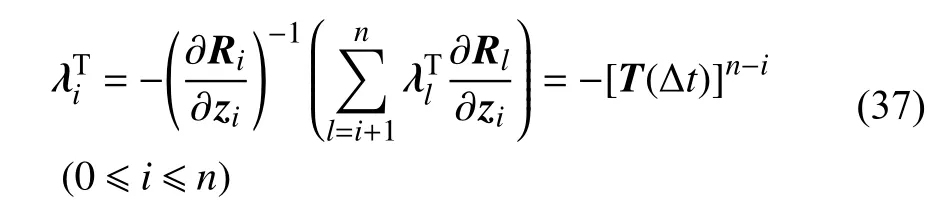
至此,按照逆向的顺序可逐步求得满足式(34)的所有伴随变量.当求取每一时刻点的所有伴随变量后,代入式(34)可消去所有含 ∂zi/∂p的隐式导数项,状态空间向量zi对设计变量p的灵敏度即为

基于上述过程,式(29)中所有导数项均为已知,因此通过适当的求积准则可得到响应函数r的近似灵敏度结果.

本方法先将目标函数在时域内进行离散,再对由离散的状态空间向量构造的扩展方程进行微分求出伴随变量,最终求出时域响应灵敏度,因此将方法称为先离散后微分的伴随变量法.

5 数值算例

本章将通过两个数值算例验证所提出的黏性阻尼系统时域响应灵敏度求解方法的正确性和有效性,并将其与基于Newmark 方法[23]所得结果进行比较,以讨论各方法在计算精度、效率和一致性问题等方面的差异.

5.1 单自由度弹簧与质量系统

考虑的单自由度系统模型如图1 所示.系统质量m=1 kg,阻尼c=0.1 N·s/m,刚度k=1 N/s,初始条件 为:u0=1 m,u˙0=0 m/s.Newmark 积分方法的参数:β=0.25,γ=0.5;MPIM 方法的参数:L=4,Ne=15,l=2.

图1 单自由度黏性阻尼弹簧-质量系统Fig.1 Single-DOF spring-mass system with viscous damping model

5.1.1 自由振动

在自由振动情形下,图1 所示的单自由度黏性阻尼系统的时域响应及其灵敏度可以解析求解得到.因此,可以利用此情形下推导出的解析解与各方法得到的数值解进行比较.本文中相对误差定义为

式中,r′为灵敏度算法计算结果,为解析解或数值参考解.当为解析解时,下文简称为相对误差,当为数值参考解时,下文简称为一致性相对误差.

分别利用基于MPIM 和Newmark 积分方案的先离散后微分和先微分后离散伴随变量法求解时域位移响应关于刚度的灵敏度,图2 为各方法在相同时间步长(Δt=0.1 s)下前20 秒的时域灵敏度相对误差.可以看到,四种方法均能得到令人满意的结果,且在相同的时间步长下,微分和离散的先后顺序对MPIM 方法的影响显著,而对Newmark 方法的影响相对较小.在所考虑的四种方法中,本文所提出的基于MPIM 的先微分后离散伴随变量法具有最高的精度.

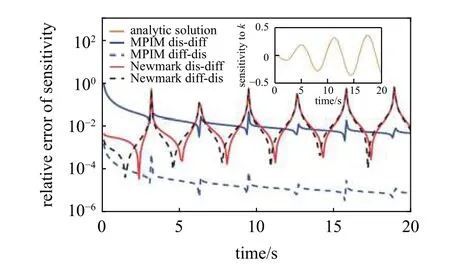
图2 相同时间步长下(Δ t=0.1 s)各方法的位移响应关于刚度灵敏度的相对误差Fig.2 The relative errors of the sensitivities of the displacement w.r.t.stiffness for different methods with the same time step

图3 和图4 分别展示了在不同时间步长下,各方法求解时域响应灵敏度的相对误差.从图3和图4 可以看出,随着时间步长减小,各方法的相对误差均逐渐降低.当时间步长相同时,基于MPIM 的先微分后离散方法精度高于对应的Newmark 方法,而基于MPIM 的先离散后微分方法精度则低于相应的Newmark 方法.在各不同时间步长下,本文所提出的基于MPIM 的先微分后离散伴随变量法仍具有最高的精度.

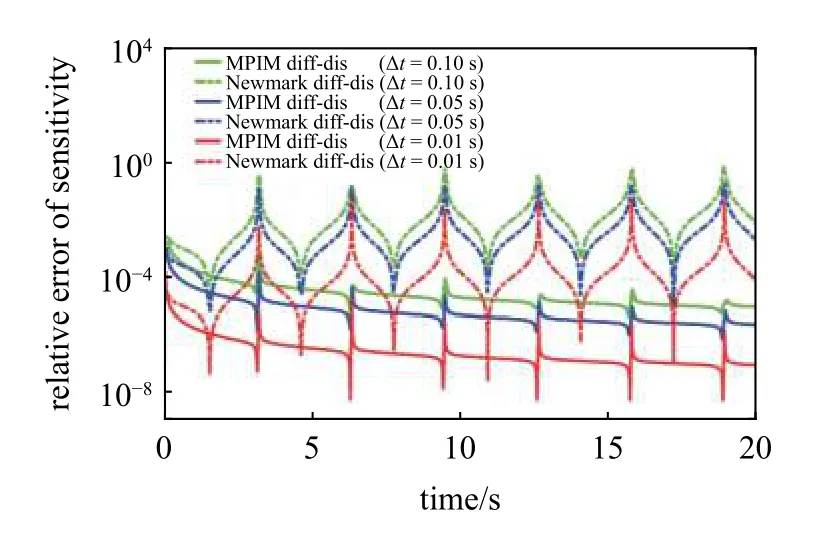
图3 不同时间步长下先微分后离散法时域灵敏度的相对误差Fig.3 The relative errors of the transient sensitivities for differentiatethen-discretize method with different time steps

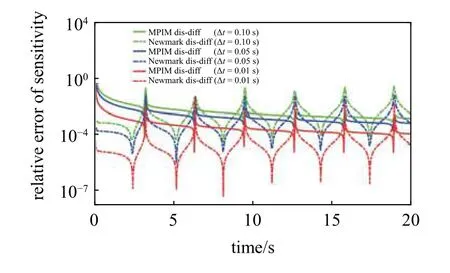
图4 不同时间步长下先离散后微分法时域灵敏度的相对误差Fig.4 The relative errors of the transient sensitivities for discretizethen-differentiate method with different time steps

接下来,对比研究各方法的计算效率.表1 展示了在不同时间步长下四种方法所花费的计算时间.可以看到,随着时间步长减小,离散步数增多,各方法所需计算时间也逐渐增多.其中,两种先微分后离散法效率更高,Newmark 先微分后离散法计算效率最高.

对于单自由度自由振动,可以推导出上述两个响应函数的灵敏度解析解.又由于上式中的各项均已求出,因此响应函数的灵敏度也可由梯形法则近似求解.在不同的步数下,利用各方法求解两个响应函数灵敏度的相对误差分别如图5 和图6 所示.首先可以看到,随着时间步长减小(步数增加),各方法计算得到的响应函数灵敏度均降低,且具有二阶收敛速度.其次,对于计算不同响应函数的灵敏度,基于MPIM 的先微分后离散伴随变量法相对误差均小于相应的先离散后微分方法,而基于Newmark 方法的伴随变量法则对不同的响应函数呈现出相反的结果.可以看出,时间步长、积分方案和微分与离散的先后顺序共同影响响应函数灵敏度相对误差.综合考虑各方法对两个响应函数灵敏度的相对误差,所提出的基于MPIM 的先微分后离散伴随变量法更优.

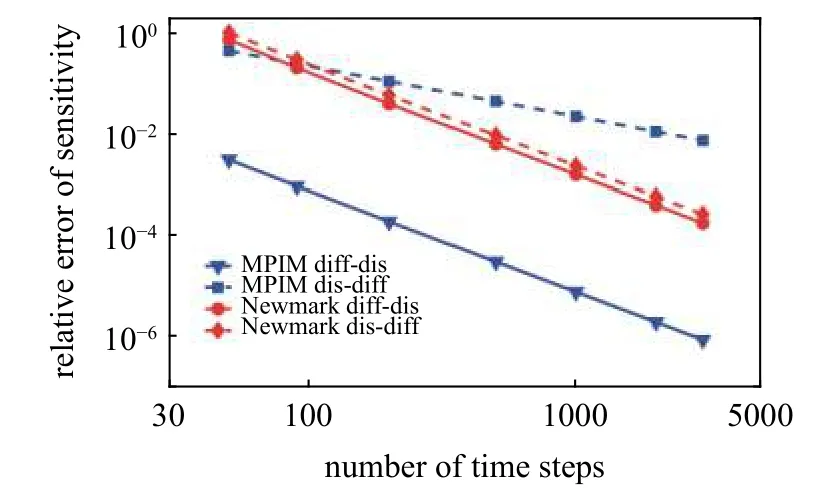
图5 响应函数 r1 关于刚度k 的时域灵敏度相对误差随离散步数变化Fig.5 The relative errors of sensitivity result for response functionr1 versus the number of time steps

图6 响应函数 r2 关于刚度k 的时域灵敏度相对误差随离散步数变化Fig.6 The relative errors of sensitivity result for response functionr2 versus the number of time steps

5.1.2 受迫振动

接着考虑受迫振动情形.假设对质量块m施加外激励f(t)=sint.对于单自由度受迫振动和多自由度系统,由于不易求得其时域响应灵敏度的解析解,因此下文均利用有限差分法(FDM)计算的时域响应灵敏度结果作为参考解,摄动量取0.01%.

分别利用4 种方法计算位移响应关于刚度和速度响应关于质量的灵敏度,其前20 s 的结果分别如图7 和图8 中小图所示.从图7 可以看出,在相同时间步长(Δt=0.1 s)和同样的离散与微分顺序下,基于MPIM 伴随变量法的一致性相对误差总体上明显小于对应的基于Newmark 方法,这一现象随着振动的持续更加明显.从图8 中,也可以得到相似的结论.综合考虑图7 和图8,从计算精度的角度看,基于MPIM 的先微分后离散方法的一致性相对误差更低.

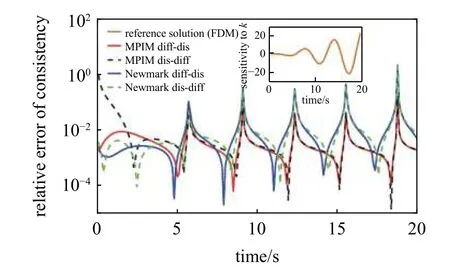
图7 相同时间步长下(Δ t=0.1 s)各方法位移响应关于刚度du/dk的灵敏度一致性相对误差Fig.7 The relative consistency errors of the sensitivities of the displacement w.r.t.stiffness d u/dk for different methods with the same time step (Δ t=0.1 s)

同时,对比受迫振动情形下各方法的计算效率.表2 展示了在不同时间步长下四种方法所花费的计算时间.结论同自由振动情形一致,随着时间步长减小,离散步数增多,各方法所需计算时间也逐渐增多.其中,两种先微分后离散法效率更高,Newmark 先微分后离散法计算效率最高.

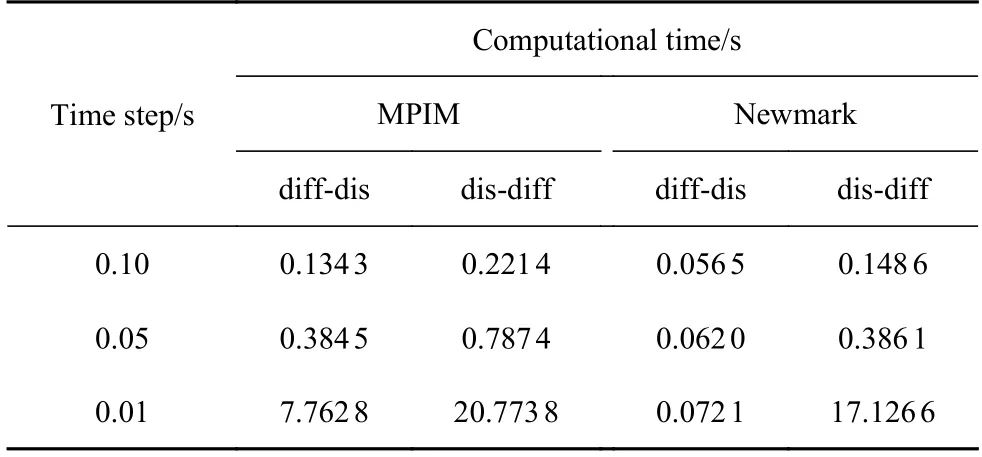
表2 受迫振动情形下各方法计算时间随步长变化对比Table 2 Comparisons of computational time for each method of forced vibration with different time steps

与自由振动情形一样,为提高计算精度,响应函数灵敏度结果使用梯形近似积分求解.在不同步数下,利用各方法求解上述响应函数灵敏度的一致性相对误差结果分别如图9 和图10 所示.可以看到,当步数相同时,基于不同积分方案的伴随变量法一致性误差明显不同,且改变MPIM 伴随变量法微分与离散的先后次序后计算结果十分相近,因此对于本例而言理论上存在的一致性问题并未对MPIM 先微分后离散法的计算精度产生明显影响.相反,在求解灵敏度时,Newmark 先微分后离散法相对误差显然低于Newmark 先离散后微分法,这说明Newmark 先微分后离散法理论上存在的一致性问题实际上提高了该方法的计算精度.由此可见积分方案同样是影响灵敏度分析结果一致性误差的重要因素.还可以观察到,在计算两类受迫振动响应函数灵敏度时,四种方法计算结果的一致性误差最终趋于相近,这说明当动力响应计算精度足够高时,一致性问题不会影响方法的可靠性.但需要指出的是,当时间步长相同时,不同积分方案所需要的计算时间相差巨大.将通过下面的轴向杆振动问题具体研究各方法的计算效率.

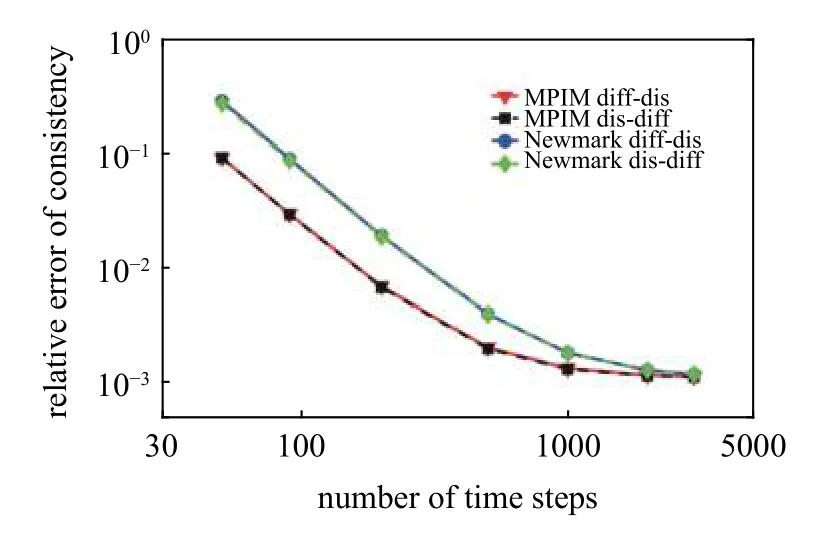
图9 响应函数 r1 关于刚度k 的时域灵敏度一致性相对误差随离散步数变化Fig.9 The relative consistency errors of sensitivity result for response function r1 versus the number of time steps

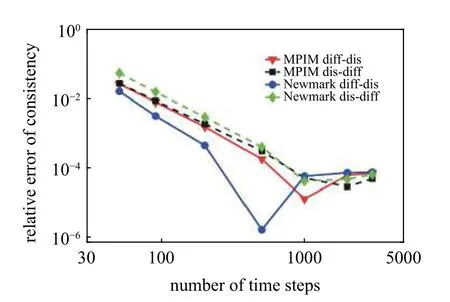
图10 响应函数 r3 关于刚度k 的时域灵敏度一致性相对误差随离散步数变化Fig.10 The relative consistency errors of sensitivity result for response function r3 versus the number of time steps

5.2 非比例黏性阻尼轴向杆问题

考虑一个非比例黏性阻尼轴向杆振动问题.该轴向振动杆简化模型如图11 所示.杆的单元质量矩阵和单元刚度矩阵分别为

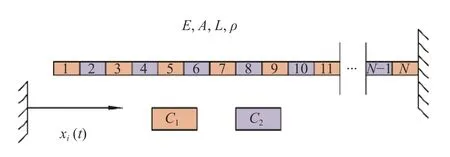
图11 非比例黏性阻尼轴向杆振动示意图Fig.11 A fixed-free axially vibrating rod with non-proportionally viscous damping model

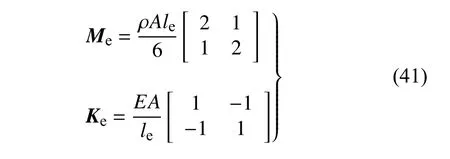
式中,ρ 表示密度,E表示材料杨氏模量,A为梁的横截面积,le=L/N为单位杆单元的长度,N为单元数,各参数分别A=6.25×10-4m2,E=2.1×104N/m2,ρ=7.8×103kg/m3.杆的全长为L=4 m .据此,杆的整体质量矩阵M和整体刚度矩阵K可组装得到.

该轴向振动杆由两种不同的阻尼材料组成,假设其阻尼模型由两种不同的比例阻尼模型描述:C1=αM+β1K和C2=αM+β2K,其中比例因子分别为 α=0.1,β1=0.001,β1=0.002 .因此,该轴向振动杆整体可看作非比例黏性阻尼系统.

首先,将上例中长为L的杆离散为80 个单元,自由振动初始条件为u0=0,u˙0=[1,0,···,0]T.分别利用基于MPIM 和Newmark 的先离散后微分和先微分后离散方法计算自由端位移响应对弹性模量E的灵敏度,其中离散时间步长均为3 ms,持续时间为前0.36 s.本例中灵敏度的参考值采用基于模态叠加法的FDM 求出(设计变量的摄动量为0.01%).图12 为四种方法时域灵敏度结果相对于参考解的一致性相对误差.可以看到MPIM 伴随变量法计算精度明显高于Newmark 伴随变量法.同时可以看出,尽管MPIM 先微分后离散法在理论上存在一致性问题,但在适当小的时间步长下,该方法计算结果一致性相对误差都能控制在相对较小的范围(E≈10-4),因此一致性问题并不影响MPIM 先微分后离散法的准确性和使用效果.

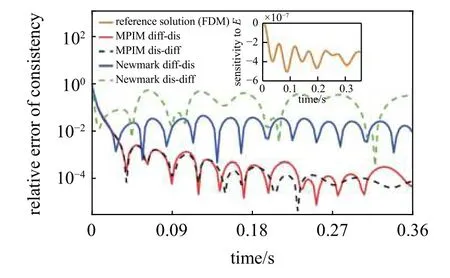
图12 各方法的位移对弹性模量 d u/dE 的灵敏度一致性对误差Fig.12 The relative consistency errors of the sensitivities of the displacement w.r.t.elastic modulus d u/dE for different methods

为了研究各方法的计算效率,可将轴向振动杆按照要求划分为不同单元数目.在时间步长为3 ms时,四种时域响应灵敏度方法的计算时间随自由度数目的变化如图13 所示.可以看到,先微分后离散方法的计算时间要比先离散后微分少得多.这是由于先离散后微分方法需要计算的伴随变量数目远多于相同步长条件下的先微分后离散方法.对于本文所考虑黏性阻尼系统,基于Newmark的先微分后离散方法具有最高的效率,而基于Newmark 的先离散后微分方法计算效率最低.而对于非黏性阻尼系统,基于MPIM 积分方案的时域响应灵敏度计算效率全面高于相同条件下基于Newmark 积分方案的方法.这是因为非黏性阻尼系统时域响应灵敏度误差主要来源于卷积型阻尼模型的近似处理,而黏性阻尼系统不含卷积型阻尼模型.虽然基于MPIM 的先微分后离散方法的计算时间略高于基于Newmark 的先微分后离散方法,但综合考虑计算精度,其仍为更推荐的时域灵敏度求解方法.

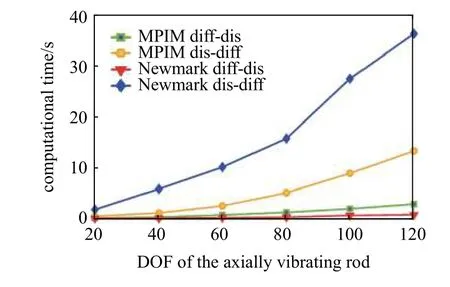
图13 各方法计算时间随自由度增加的变化Fig.13 Calculation time of different DOF for the compared methods of the axially vibrating rod

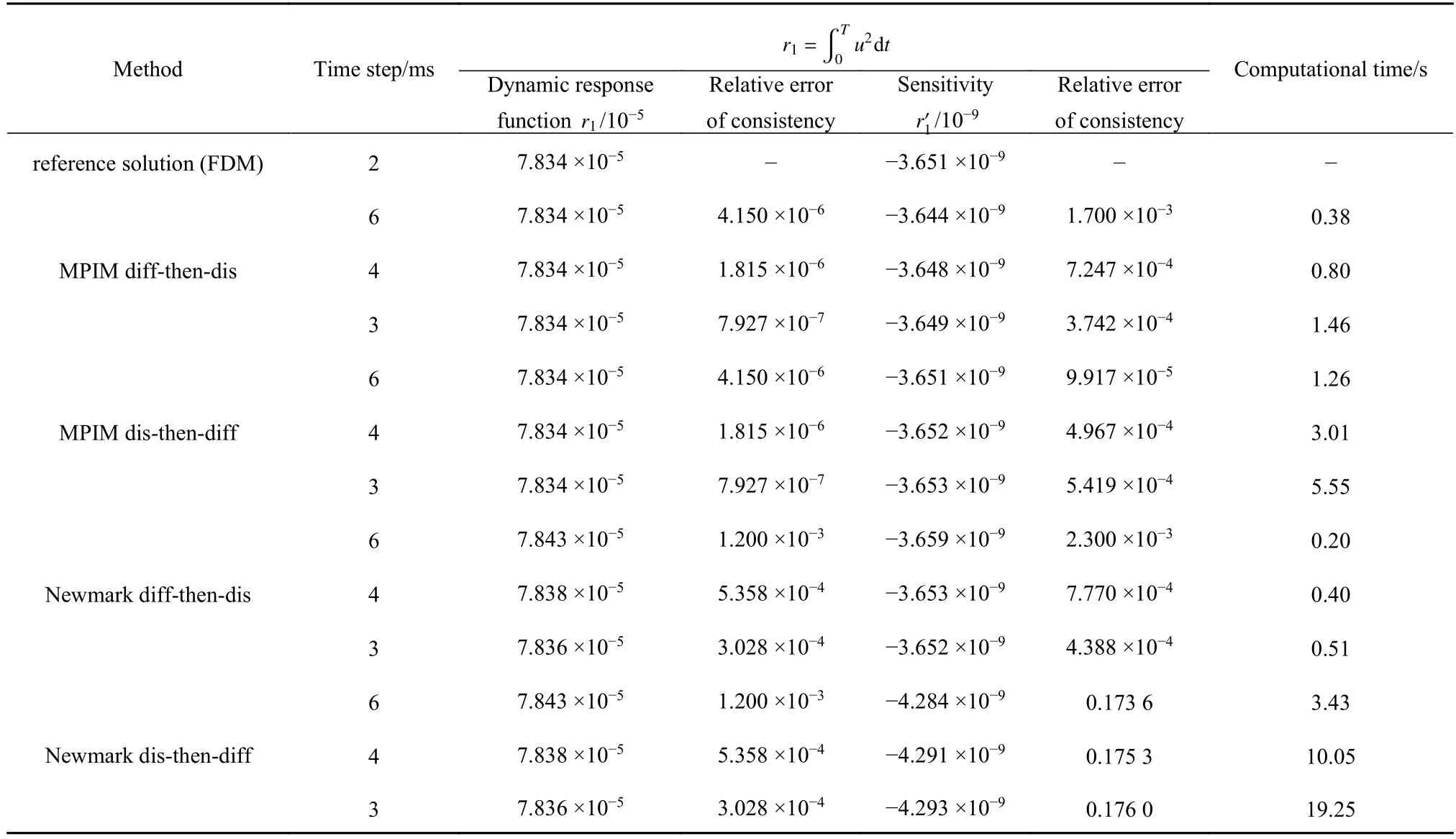
表3 各方法在不同时间步长下响应函数及其灵敏度计算精度及时间比较Table 3 Comparisons of the relative consistency errors for response function r1 and its sensitivity w.r.t.stiffness with different time steps using various methods

6 结论

(1)基于MPIM 的先离散后微分和先微分后离散方法均能得到准确可靠的时域响应灵敏度结果.因此本文推导出的两种方法可有效的求解黏性阻尼系统时域响应灵敏度.

(2)对于黏性阻尼系统时域响应灵敏度求解问题,在相同时间步长和离散与微分顺序下,基于MPIM 积分方案的计算精度高于基于Newmark 积分方案的结果.该差异由各积分方案自身求解精度所致.对于本文所给出的基于MPIM 的时域响应灵敏度求解方法,先微分后离散方法的精度高于先离散后微分方法.

(3)对于黏性阻尼系统时域响应灵敏度求解,基于MPIM 和Newmark 方法的先微分后离散方法均存在一致性误差,改变微分和离散的先后次序对两方法一致性误差的作用不完全一致.通过减小时间步长也可降低算法的一致性误差.当动力响应计算精度足够高时,一致性问题并不会影响时域灵敏度求解方法使用的可靠性.

(4)虽然MPIM 先微分后离散法计算效率略低于Newmark 先微分后离散法,但在相同条件下,前者对时域响应函数及灵敏度的计算精度远高于后者.综合考虑精度、效率和一致性问题,本文给出的基于MPIM 的先微分后离散伴随变量法表现更优,最适合应用于黏性阻尼系统时域梯度优化算法.