复合干摩擦的准零刚度隔振系统的亚谐共振1)

牛江川 张婉洁 申永军 王军

(石家庄铁道大学交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)

(石家庄铁道大学机械工程学院,石家庄 050043)

引言

由于工程中存在的巨大需求,振动控制技术一直是研究热点[1].隔振技术是振动控制的主要手段之一,而非线性隔振可以改善隔振系统的性能,因此成为了隔振技术的研究热点.陆泽琦和陈立群[2]综述了近年来非线性隔振理论和应用的研究进展,以及高静态低动态刚度隔振及其非线性阻尼加强形式和双层非线性隔振.高雪等[3]以分段双线性分段光滑隔振系统为理论模型,系统研究了摒除不利于隔振的非线性动力学现象设计方法.Ding等[4]利用解析法和数值法研究了具有弹性支承端的黏弹性梁的隔振.

由于准零刚度非线性隔振系统具有宽频带隔振特性,因此受到了学者们的广泛关注[5-13].目前学者们主要研究准零刚度隔振系统的结构,单频激励下的力和位移传递特性及幅频响应特性,隔振性能的提高以及其在不同领域中的推广应用.在准零刚度结构设计方面,徐道临等[14]设计了一种具有高静态刚度、低动态刚度的非线性低频隔振器,并利用谐波平衡法分析了系统的动力学特性,推导了系统的力传递率.Wang等[15]提出了一种相当紧凑的准零刚度隔振器,由一对相互排斥的磁环和一个节省空间的波形弹簧并联而成.Gao 和Teng[16]针对重型机械低频干扰振动的隔离问题,提出了一种以波纹管结构为弹性元件,以加压气体和不可压缩液体为工作介质的高静态低动态刚度油气隔振器.Wang等[17]提出了一种具有双准零刚度机构的新型非线性超低频隔振器.在准零刚度隔振性能的提高方面,Wen等[18]通过半主动控制策略对准零刚度隔振系统进行控制以扩大其有效位移范围.Zhang等[19]通过附加惯容非线性能量阱克服准零刚度隔振系统中较小的动态刚度可能导致的低频振动.Liu等[20]通过引入可调谐非线性惯容来增强准零刚度隔振系统的隔振性能.Donmez等[21]通过在准零刚度隔振系统中的垂直弹簧上串联干摩擦阻尼,降低准零刚度隔振系统在共振区域的传递率.在准零刚度隔振的推广应用方面,Ding 和Chen[22]分析了准零刚度隔振器对初始弯曲结构多模态弯曲振动的隔振效果.赵含等[23]建立了基于准零刚度隔振器的推进轴系纵振动力学模型,应用谐波平衡法求解出系统的力传递率.赵权等[24]研制了一种空间占比小的准零刚度车载隔振系统,采用平均法求解了系统在车体简谐位移激励下的动力学响应以及位移传递率.

准零刚度结构引入的非线性刚度特性在单频激励下可能引起系统的次共振.例如,Liu 和Yu[25]利用半解析法和数值法研究了准零刚度隔振系统周期1 响应中存在的超谐共振.另外,由于干摩擦阻尼减振技术在工程中应用广泛[26-29],因此本文通过干摩擦阻尼器对准零刚度非线性隔振系统的共振响应进行控制.首先利用平均法求解复合干摩擦阻尼器的准零刚度隔振系统在简谐激励下的主共振近似解析解,然后再根据增量方程求解系统的1/3 次亚谐共振近似解析解.推导系统的幅频响应方程,分析定常解的稳定性,并获得系统主共振和亚谐共振的力传递率.然后详细分析准零刚度和干摩擦阻尼的振动抑制以及隔力效果.

1 系统模型

复合干摩擦阻尼器的准零刚度非线性隔振系统的物理模型示意图如图1 所示.图1中m表示系统的质量,c是隔振系统的等效线性黏性阻尼,k和k1分别表示隔振系统垂直弹簧的线性刚度和水平弹簧的线性刚度,fc为干摩擦阻尼器提供的库伦摩擦力.Fcosωt表示外部激励,其中F为激励幅值,ω为激励角频率.Lh为质量块处于静平衡位置时水平弹簧的长度,水平弹簧的原始长度为L0.

图1 准零刚度隔振系统模型Fig.1 Quasi-zero-stiffness vibration isolation system model

水平弹簧在垂直方向提供的弹性恢复力可以表示为

根据牛顿第二运动定律,建立准零刚度隔振系统在外部激励下的动力学运动方程

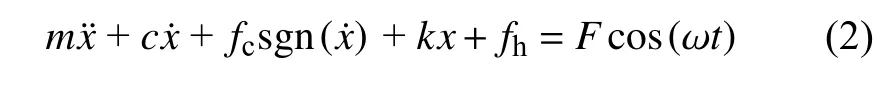
为了方便求解式(2),将式(1)写成多项式形式.利用泰勒公式将式(1)在x=0 处展开,式(1)可以表示为

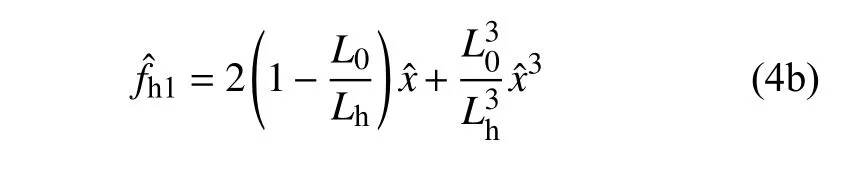
令Lh=0.7L0,根据式(4a)可以得水平弹簧在垂直方向弹性恢复力的值,根据式(4b)得到其三阶近似值,如图2 所示.从图中可以看出,当x≤0.2L0时三阶近似可以很好的表示水平弹簧在垂直方向的恢复力.

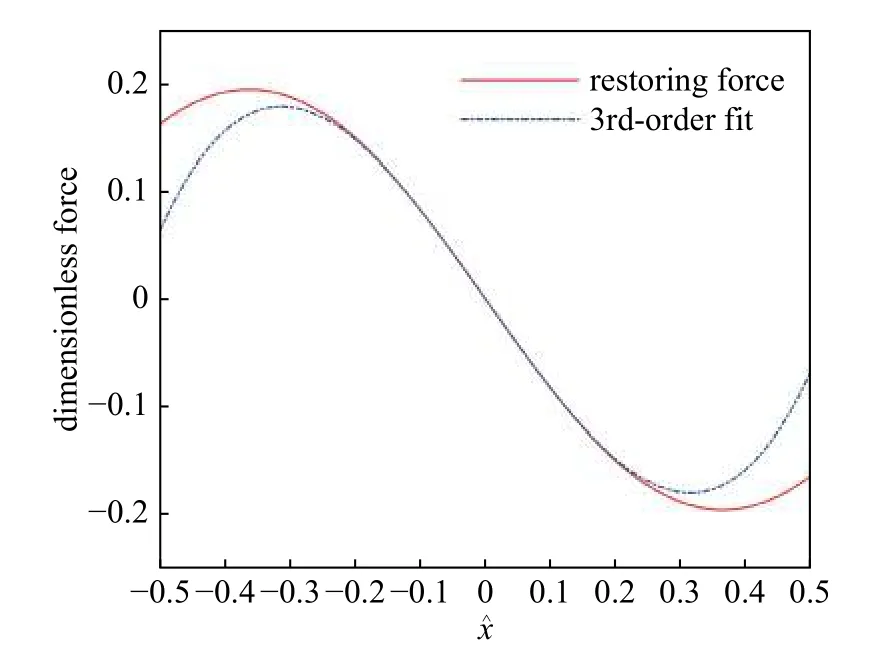
图2 水平弹簧在垂直方向的弹性恢复力位移曲线Fig.2 Restoring force-displacement curve of horizontal springs in vertical direction

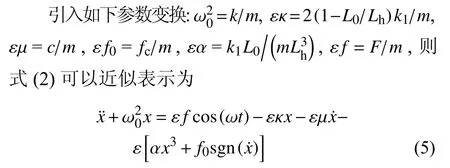
2 主共振

首先利用平均法求解准零刚度隔振系统的主共振近似解析解,并分析主共振定常解的稳定性.

2.1 主共振近似解析解

研究复合干摩擦的准零刚度隔振系统的主共振,并令

设式(7a)的周期解为

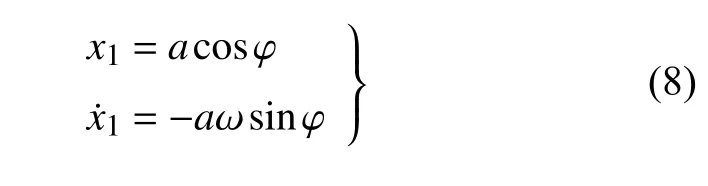
其中,φ=ωt+θ,振幅a和相位θ随t缓慢变化.

根据平均法可以得到一个振动周期T=2π/ω 内振幅和相位的平均值为

首先计算式(9)的第一部分,可以得到

计算式(9)的第二部分时,需要分为两种情况:振幅a＞0 和a＜0 .当振幅a＞0 时,可以得到

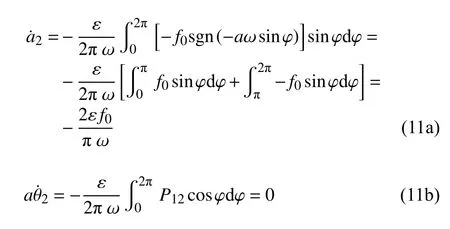
类似地,可以计算振幅a＜0 的情况.于是,式(9)的第二部分可以表示为

联合式(10)和式(12),并替换含有小参数的变量,可以得到

2.2 定常解及其稳定性

将系统主共振稳态运动的定常解振幅和相位分别表示为和,令式(13)中的=0 和=0,可以得到系统的稳态运动方程

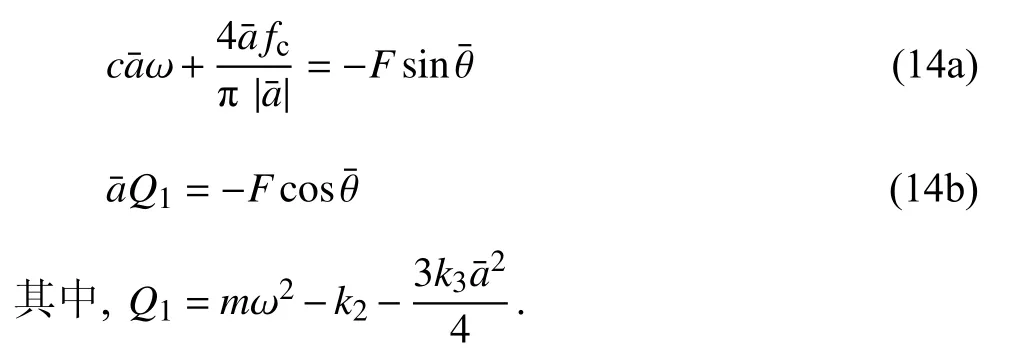
根据式(14)可以得到复合干摩擦的准零刚度隔振系统主共振的幅频响应方程和相频响应方程

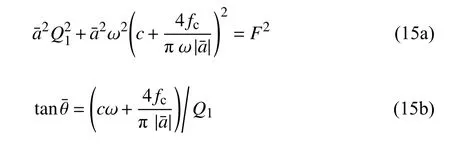
从式(15a)中可以看出,准零刚度结构通过负线性刚度的形式改变系统的等效固有频率使其为0.摩擦力以等效阻尼的形式影响系统的主共振幅频响应,其值与激励频率以及振幅有关.而且稳态振幅越小,摩擦力的等效阻尼越大.

利用式(14)消去式(16)中的三角函数,进一步得到准零刚度隔振系统主共振的特征方程为

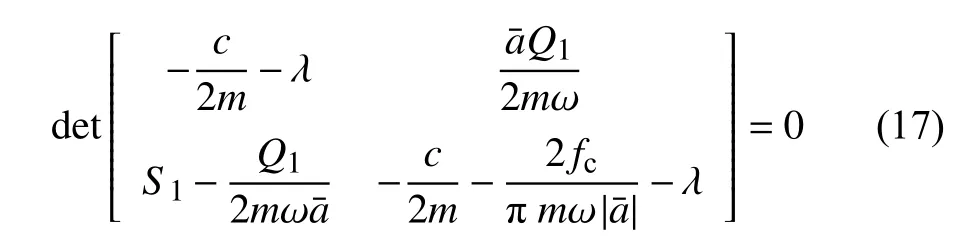
将式(17)中的行列式展开,得到准零刚度隔振系统主共振稳态响应的特征方程为

由于c/m+2fc/(πmω|)＞0,于是可以得到复合干摩擦的准零刚度隔振系统主共振定常解渐近稳定的条件为

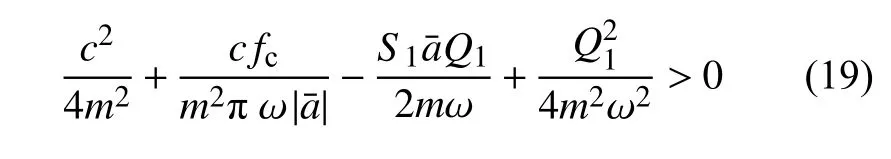
3 亚谐共振

在准零刚度隔振系统主共振近似解析解的基础上得到系统的增量方程,利用平均法计算系统的1/3 次亚谐共振近似解析解,并分析亚谐共振定常解的稳定性.

3.1 亚谐共振近似解析解

在主共振响应的基础上,研究复合干摩擦的准零刚度隔振系统的1/3 次亚谐共振.首先,计算增量方程.令

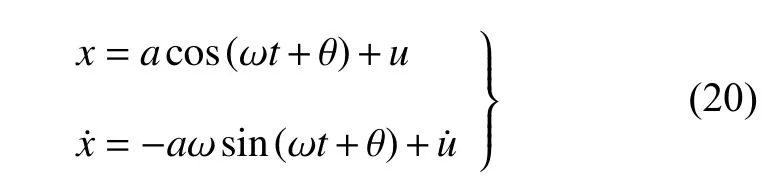
将其代入到式(5)中,并利用主共振近似解析解进行化简,消去其同次谐波项,可以得到

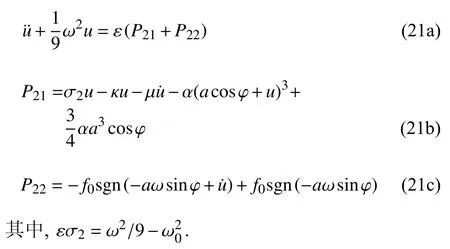
设式(21a)的周期解为

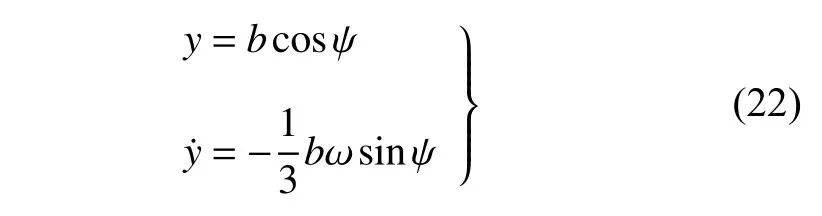
其中,ψ=ωt/3+ϑ .

根据平均法可以得到一个公共振动周期T0=6π/ω内振幅和相位的平均值为

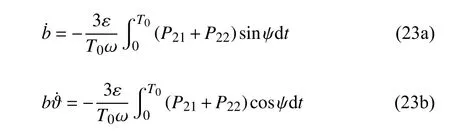
计算式(23)的第一部分,可以得到

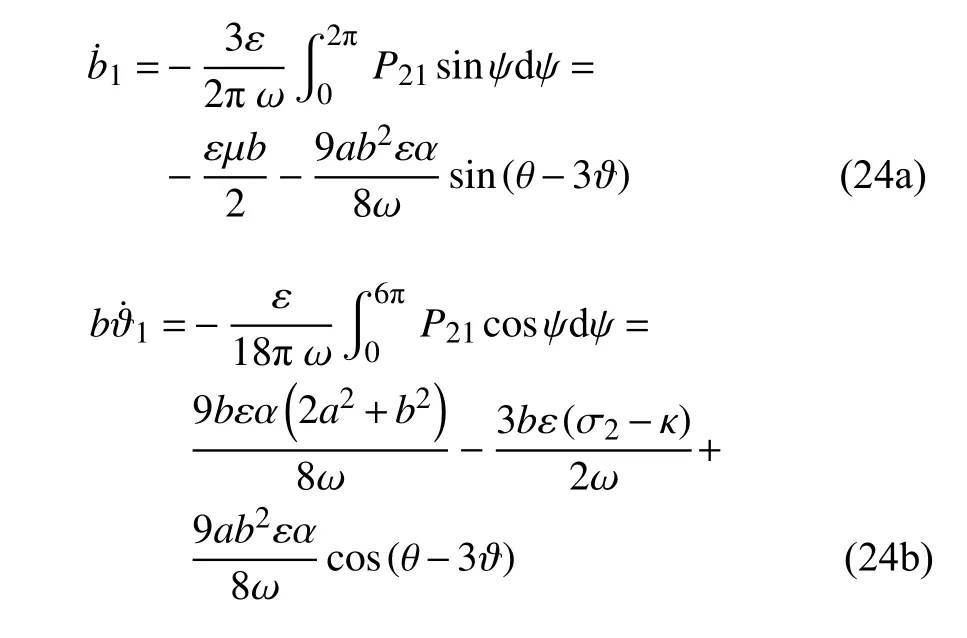
直接计算式(23)的第二部分比较困难,因此引入符号函数的一阶泰勒公式[30]

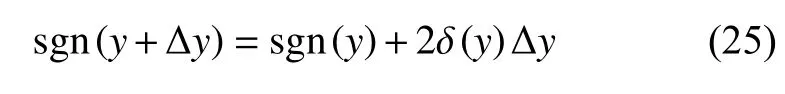
其中,δ (y) 为关于变量y的狄拉克函数.

根据式(25),P22可以近似为

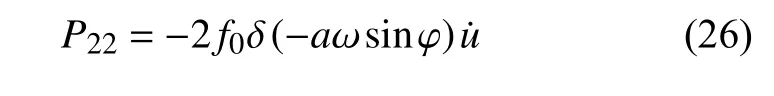
将式(26) 中的狄拉克函数利用傅里叶级数展开,可以得到

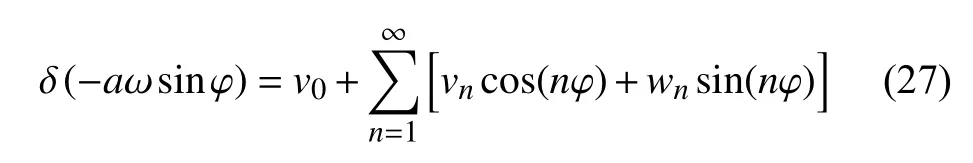
其中,v0,vn和wn为傅里叶系数.其周期为T1=π/ω .

计算傅里叶系数,可以得到

于是,式(27)可以表示为

计算式(23)的第二部分,可以得到

联合式(24)和式(30),并替换含有小参数的变量,可以得到

3.2 亚谐共振的定常解

根据式(32)可以得到准零刚度隔振系统1/3 次亚谐共振的幅频响应方程和相频响应方程

从式(33a)中可以看出,摩擦力以等效阻尼的形式影响系统的亚谐共振幅频响应特性,其值与激励频率以及主共振的振幅有关.

于是可以得到准零刚度隔振系统的1/3 次亚谐共振的近似解析解

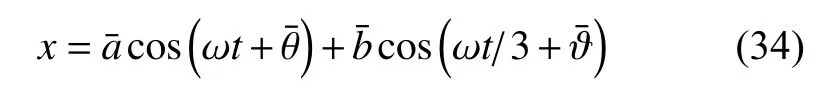
其中,和由式(15)确定,和由式(33)确定.需要注意的是,由于在推导幅频响应方程的过程中进行了平方处理,所以根据幅频响应方程计算的解析解数量会增多,因此需要将其代入稳态运动方程进行验证.

3.3 定常解的存在条件及其稳定性

首先分析准零刚度隔振系统1/3 次亚谐共振定常解的存在条件.令z=,将准零刚度隔振系统的幅频响应方程重新整理为

根据一元二次代数方程存在正实根的条件,可以得到1/3 次亚谐共振的存在条件为

显然,式(36)中的第二个条件覆盖了第一个条件.因此,准零刚度隔振系统1/3 次亚谐共振定常解的存在条件可以重新整理为

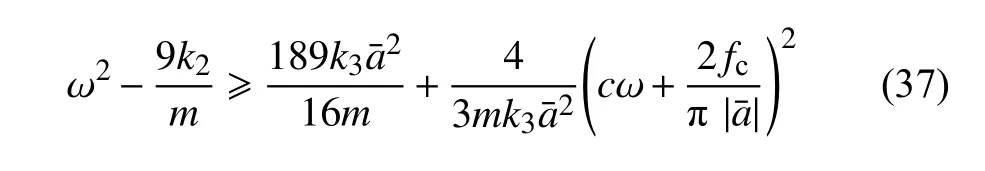
当k2=0 时,激励频率满足式(37)准零刚度隔振系统就会存在1/3 次亚谐共振.显然,亚谐共振的存在条件与主共振的振幅以及摩擦力相关.

利用式(32)消去式(38)中的三角函数,进一步得到系统亚谐共振的特征方程为

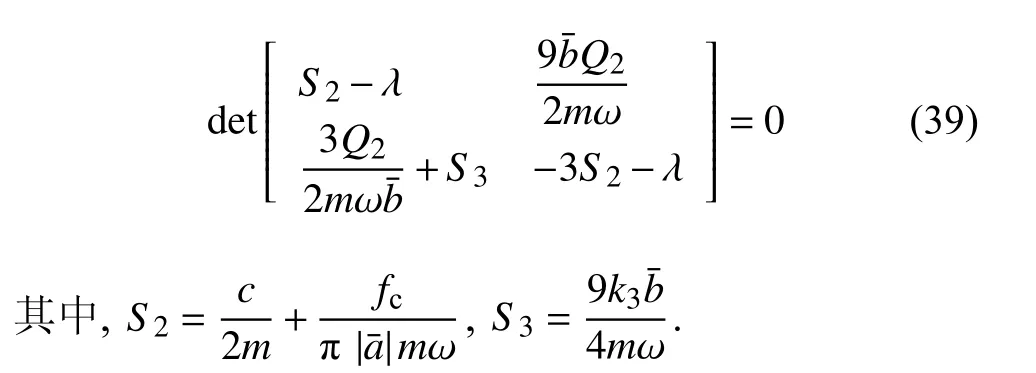
将行列式展开,得到系统1/3 次亚谐共振的特征方程为

由于S2＞0,于是可以得到准零刚度隔振系统1/3 次亚谐共振定常解渐近稳定的条件为

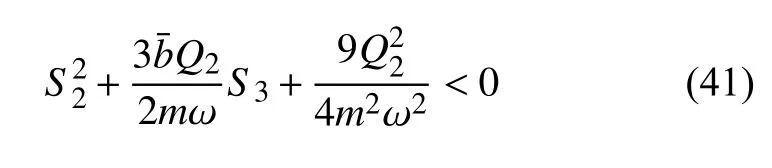
4 力传递率

根据图1 所示的准零刚度隔振系统模型,传递到基础的合力G可以表示为

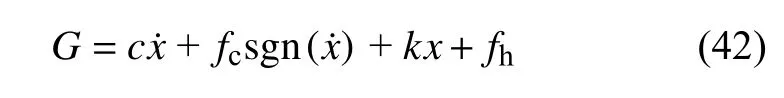
利用传递到基础的力幅值和激励幅值的比值表示力传递率.于是,可以得到准零刚度隔振系统的力传递率为

其中,‖‖ 表示对力取模.

根据主共振的近似解析解,可以得到准零刚度隔振系统主共振的力传递率为

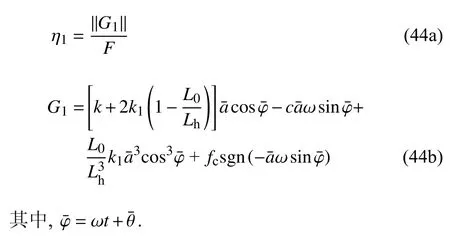
根据亚谐共振的近似解析解,可以得到准零刚度隔振系统1/3 次亚谐共振的力传递率为

根据式(2),式(42)可以重新表示为

于是,可以得到准零刚度隔振系统力传递率的另外一种表示形式

从式(47) 中可以直观的看出当外部激励幅值F≠0且=0 时,力传递率 η=1 .

5 数值解验证

根据文献[19]选取一组准零刚度隔振系统的参数:m=60 kg,c=200 N·s/m,k1=2179 kN/m,Lh/L0=0.7,k=2(L0/Lh-1)k1=1867.7 kN/m,L0=0.5 m,F=1 kN.根据式(2)利用龙格库塔法分别绘制摩擦力fc=0 N和fc=50 N 时系统的幅频响应曲线,如图3 所示.图中的横坐标为激励频率与原线性系统固有频率的比值,即 γ=ω/ω0.根据式(15) 和式(34),利用近似解析解绘制系统的主共振(primary resonance,PR) 和1/3 次亚谐共振(subharmonic resonance,SR)的幅频响应曲线,并根据稳定性条件分别得到稳定解和不稳定解.从图3 中可以看出,无论是否存在干摩擦力的作用,准零刚度隔振系统的主共振和亚谐共振的幅频响应的近似解析解和数值解都具有很好的一致性.准零刚度隔振系统的主共振响应中存在明显的幅值跳跃现象.准零刚度隔振系统的亚谐共振仅在一定激励频率范围内存在,而且出现在主共振区域.当无摩擦阻尼器时,从数值解中还可以看出比较明显的超谐共振以及其他低次亚谐共振.当复合干摩擦阻尼器时,不但使得系统的1/3 次亚谐共振区域变小,并且消除了其他低次的亚谐共振.

图3 幅频响应响应曲线对比Fig.3 Comparison of amplitude-frequency response curves

图3 幅频响应响应曲线对比(续)Fig.3 Comparison of amplitude-frequency response curves (continued)

根据式(2),利用数值解分别绘制摩擦力fc=0 N和fc=50 N 时准零刚度隔振系统传递到基础的力传递率曲线,如图4 所示.根据式(44)和式(45),利用近似解析解绘制系统的主共振和1/3 次亚谐共振的力传递率曲线.从图4 中可以看出,无论是否存在干摩擦力的作用,准零刚度隔振系统的主共振和亚谐共振的力传递率的近似解析解和数值解也都具有很好的一致性.通过复合干摩擦阻尼器,使得准零刚度隔振系统的亚谐共振力传递频带变小,但是也增大了系统在有效隔振频带内的主共振力传递率.

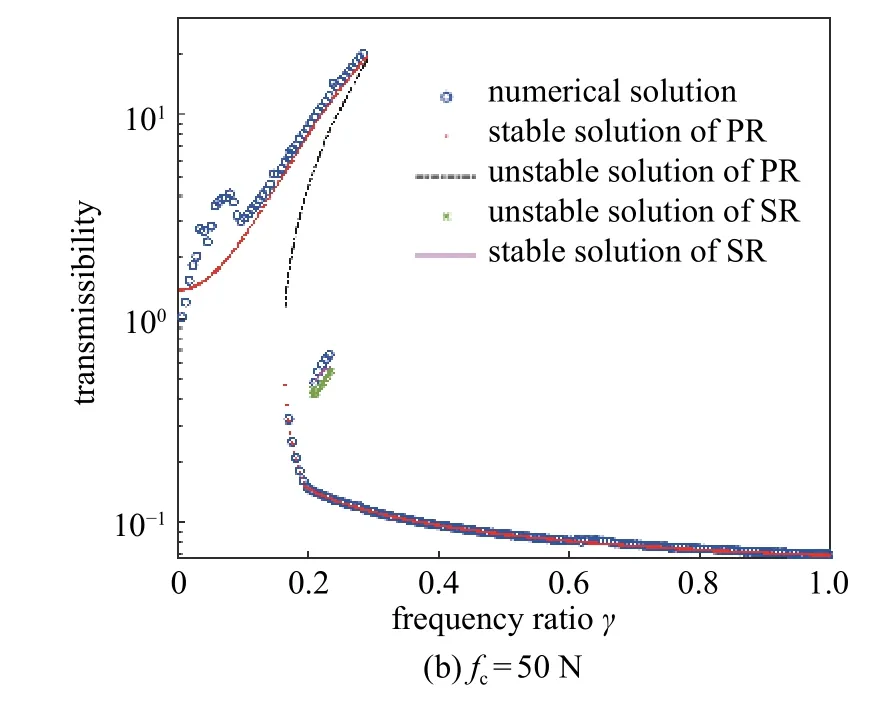
图4 力传递率对比Fig.4 Comparison of force transmissibility

6 振动控制效果分析

接下来利用近似解析解分析准零刚度参数以及干摩擦阻尼对准零刚度隔振系统幅频响应和力传递特性的影响.

6.1 准零刚度参数的影响

当干摩擦力fc=0 N 时,利用近似解析解分别绘制原线性系统(表示为L0=0 m),以及准零刚度水平弹簧原长分别为L0=0.1 m,L0=0.5 m 以及L0=1 m 时,系统的主共振和亚谐共振幅频响应曲线及力传递率曲线,如图5 所示.为了使对比效果更清晰,图中仅显示准零刚度隔振系统的稳定解.从图5(a)中可以看出,由于引入准零刚度隔振器,使得系统的共振频率向低频处转移,因此对于高频激励起到了很好的振幅抑制效果.随着准零刚度水平弹簧原长的增大,主共振峰值逐渐变大,主共振频率逐渐减小,亚谐共振的区域也逐渐变小.从图5(b)中可以看出,准零刚度隔振器明显降低了原系统的起始隔振频率.准零刚度水平弹簧原长越大,有效的起始隔振频率越低,而且最大力传递率也越小.

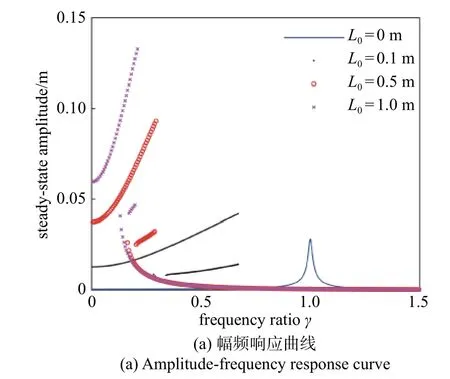
图5 不同准零刚度参数的振动控制效果Fig.5 Effect of different quasi-zero-stiffness parameters

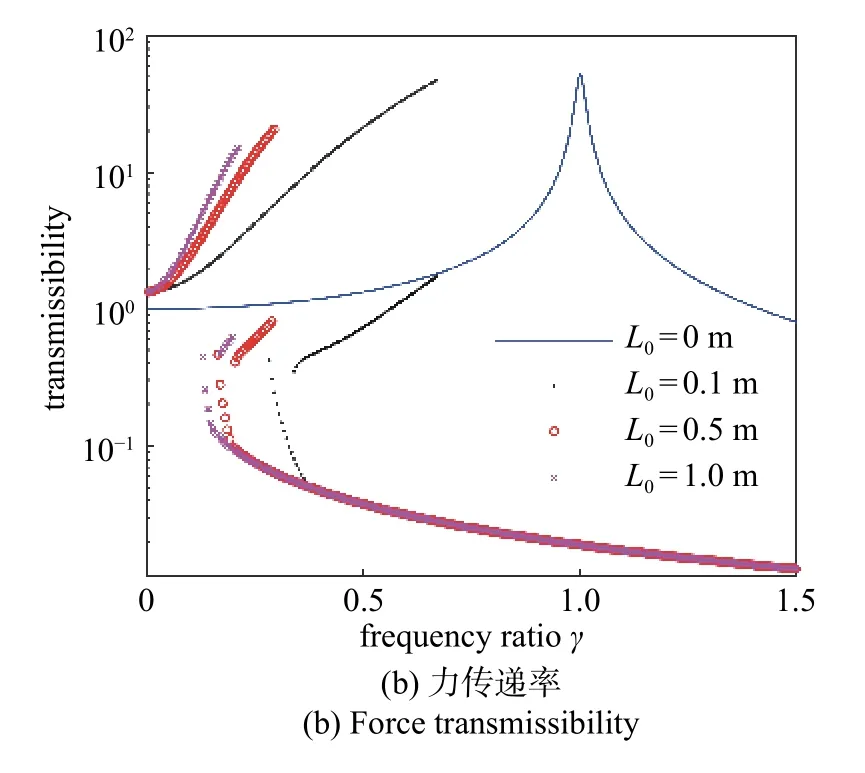
图5 不同准零刚度参数的振动控制效果(续)Fig.5 Effect of different quasi-zero-stiffness parameters (continued)

6.2 干摩擦的影响

当准零刚度水平弹簧原长为L0=0.5 m 时,利用近似解析解分别绘制准零刚度隔振系统在干摩擦力fc=0 N,fc=100 N 以及fc=500 N 时,系统的主共振和亚谐共振幅频响应曲线及力传递率曲线,如图6所示,图中同样仅显示系统的稳定解.从图6(a)中可以看出,随着干摩擦力的增大,不但可以消除准零刚度隔振系统的亚谐共振,而且能够有效降低主共振的幅值.从图6(b)中可以看出,随着摩擦力的增大,准零刚度隔振系统的起始隔振频率逐渐减小.同时,干摩擦力会导致准零刚度隔振系统在有效隔振频率范围内的力传递率增大.特别是当外部激励无法克服干摩擦的作用时,系统的振幅为0,但是系统的力传递率为1,也就无法起到隔力的效果.

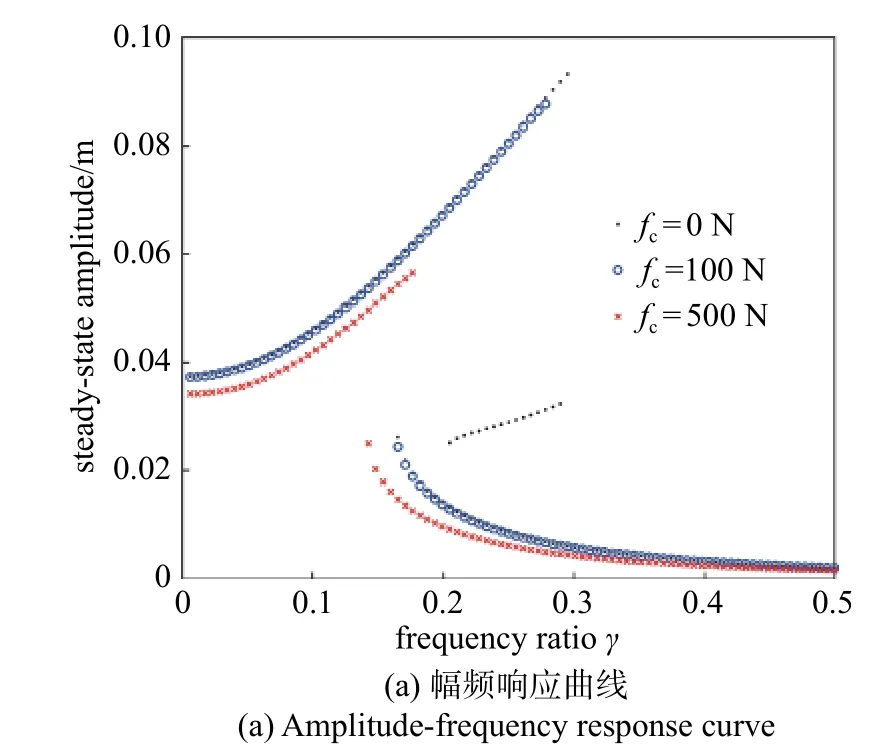
图6 不同干摩擦力的振动控制效果Fig.6 Effect of different dry friction force

7 结论

本文利用增量平均法研究了复合干摩擦阻尼器的准零刚度隔振系统的1/3 次亚谐共振.通过幅频响应方程可以看出,干摩擦力以等效阻尼的形式影响系统的主共振和亚谐共振的幅频响应.对系统稳态解的稳定性进行了判断,并推导了准零刚度隔振系统亚谐共振的存在条件.通过与数值解获得的准零刚度隔振系统的幅频响应曲线进行对比,验证了主共振和亚谐共振近似解析解的准确性.准零刚度隔振系统的亚谐共振被转移到了低频处的主共振区域,并且可以通过增大干摩擦力消除系统的亚谐共振.通过比较系统的幅频响应和力传递率,可以发现:准零刚度水平弹簧原长越大,起始隔振频率越低,但是在低频处的主共振振幅越大;干摩擦力的引入,不但可以有效抑制准零刚度隔振系统的共振振幅,而且可以降低系统的起始隔振频率,但是会导致系统在有效隔振频带内力传递率的增大.因此,当以准零刚度隔振系统的振幅抑制为目标时,可以选用干摩擦阻尼器;当以降低系统的力传递率为目标时,不宜选用干摩擦阻尼器.