环形节流静压止推气体轴承承载力和刚度分析
孙哲哲 王一斐 黄 凯 赵红利
(西安交通大学能源与动力工程学院 陕西西安 712046)
由于气体轴承速度高、精度高、使用寿命长、摩擦功耗小,在工业领域的应用越来越广泛[1]。然而其承载力比同类的油润滑轴承要低[2-3],因此很有必要探究气体轴承承载力和刚度的影响因素,并据此对气体轴承进行优化以提高承载力和刚度。
气体轴承承载力低的主要原因是当轴承间隙和供气压力增大时,轴承气流会出现从亚音速向超音速的跨越,导致轴承气膜压力骤减,甚至出现负压,进而影响轴承的刚度和承载力。MORI[4]将气膜内的流场分为超音速流动阶段、亚音速流动阶段和黏性等温流动阶段,采用柱对称的超音速流动正激波解释了这种压力骤降现象,并通过实验得出在小孔入口处增加圆形或者锥形倒角可以使压力曲线变得平缓的结论。但在相关实验中作者没有发现这种具有强间断面的正激波。1969年MORI和MIYAMATSU[5]又采用拟激波理论研究了这种压力骤降现象,他们忽略了激波导致的熵增,得到的结果和试验基本一致。BOFFEY和WILSON[6]实验研究了气体轴承气穴边缘的压力,观察到气体压力下降的幅度和速度增加的幅度相一致。POUPARD和DROUIN[7]研究发现,利用实验结果得到的平均摩擦因数可以很好地拟合压力下降曲线,但是无法解释压力下降的原因。
随着计算机技术的飞速发展,人们开始利用数值方法求解雷诺方程以得到更准确的流场分布。STAHLER[8]和DOWSON[9]分别从理论和实验方面证实了超音速流动的存在,以及超音速通过激波向亚音速流动的过渡。YOSHIMOTO等[10]通过模拟呈现了轴承入口流域的流动结构,并认为超音速到亚音速的流动状态是通过气流的重新分层而不是通过激波来实现的。ELESHAKY[11]模拟求解了三维湍流可压缩空气的N-S方程,展示了轴承入口区域压缩波形成激波和激波相互作用的过程,发现空气通过激波区域由超音速转变成亚音速,在此过程中流体也重新分层。
综上,目前研究大多是针对常规尺寸气体轴承的数值模拟,但开发重载气体轴承是轴承技术发展的必然趋势。本文作者利用SolidWorks建立气体止推轴承的模型,借助FLUENT平台对大直径、双排孔气体止推轴承进行数值模拟。文中首先分析了不同供气压力和轴承间隙下轴承承载力和刚度变化,之后结合间隙内的流场和压力分布进行对比分析,并探究提高大型重载静压气体止推轴承承载力和刚度的方法。
1 气体止推轴承模型的建立
1.1 模型建立
在一定供气压力和气膜厚度下,轴承的结构参数决定了气体在轴承间的流动状态,从而决定了轴承的承载能力、刚度和气体流量等。静压气体止推轴承的结构如图1所示。结构参数为:轴承外径为150 mm,内径为75 mm,节流孔直径为0.35 mm。外部供给气体从节流小孔进入止推轴承和止推盘之间的间隙,在其中形成气膜,之后再流入外界环境。具体参数如表1所示。
研究轴承的静态性能,是指通过研究气体在轴承间隙中的流动状态得到气膜压力分布情况和承载力的大小。因此以气体轴承为研究对象,同时考虑对称性和周期性,由于轴承单排小孔数为18个,所以取气膜的1/18建立模型[2],如图 2所示。

图2 静压气体止推轴承结构简化图
1.2 FLUENT求解模型的设置
采用Workbench mesh进行网格划分,划分网格前,先对模型进行分割,对分割后的模型进行扫掠划分网格。因为模型厚度方向尺寸和其余2个方向相差较大,扫掠时应注意控制气膜厚度方向上的网格层数,当厚度方向上网格大于7层时,网格参数较理想,划分效果如图3所示。
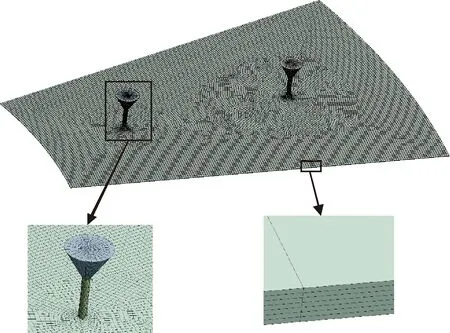
图3 轴承网格划分示意
进气孔的入口采用压力入口边界条件,给定温度和压力,进口设置如图 4所示。出口采用压力出口条件,在出口截面给定环境压力。轴承表面和止推盘表面选用无滑移壁面边界条件,对称面上选用周期性边界条件。由于小孔周围的压力梯度很大,因此压力项的求解选用PRESTO![12]。

图4 模拟进口设置
2 仿真结果及分析
考虑到供气压力和气膜厚度对承载力和刚度产生的影响,气膜厚度分别取5、10、20、30、40和50 μm,供气孔直径取0.35 mm,供气压力分别取0.25、0.35、0.45和0.6 MPa进行模拟。
2.1 供气压力对轴承压力分布、刚度和承载力的影响
2.1.1 气膜压力场分布变化
不同供气压力下气膜压力分布如图5所示。

图5 不同气膜厚度下气膜压力分布随供气压力变化云图
由图5可以看出:不同气膜厚度时,压力分布随着供气压力变化的规律相同:供气孔处压力最大,沿径向方向压力逐渐下降至环境压力。随着供气压力的增大,轴承上相同位置处的压力增大。
为了进一步观察分析压力的径向变化情况,在供气孔中心所在位置取一条径向线,并做出压力变化曲线,如图6所示。
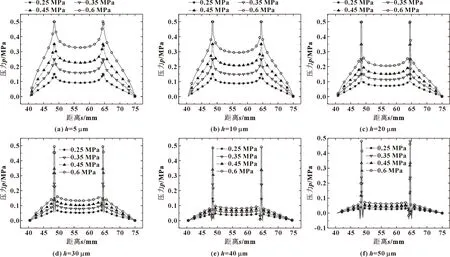
图6 不同气膜厚度下气膜压力分布随供气压力变化
从图6中可以看出,在气膜厚度为5和10 μm时,随着供气压力的增大,轴承上相同位置处的压力都在增大;当气膜厚度大于20 μm时,压力在小孔周围先骤降,然后又快速升高到大气压力以上,最后再逐渐降低至大气压力,且随着供气压力的增大,小孔附近压力的最小值逐渐减小。根据文献[13]可知,这是因为供气压力过大和气膜厚度过大导致轴承入口处气流速度过快,出现了压力的骤减。
2.1.2 气膜刚度和承载力大小变化
图7所示为不同气膜厚度下气膜刚度随供气压力的变化曲线。气膜厚度为5、10、20、30和40 μm时,随着供气压力的增加,刚度不断增加,且随着气膜厚度的增大,刚度增加趋势减缓;当气膜厚度达到50 μm时,随着供气压力的增加,刚度呈现先增大后减小的趋势。
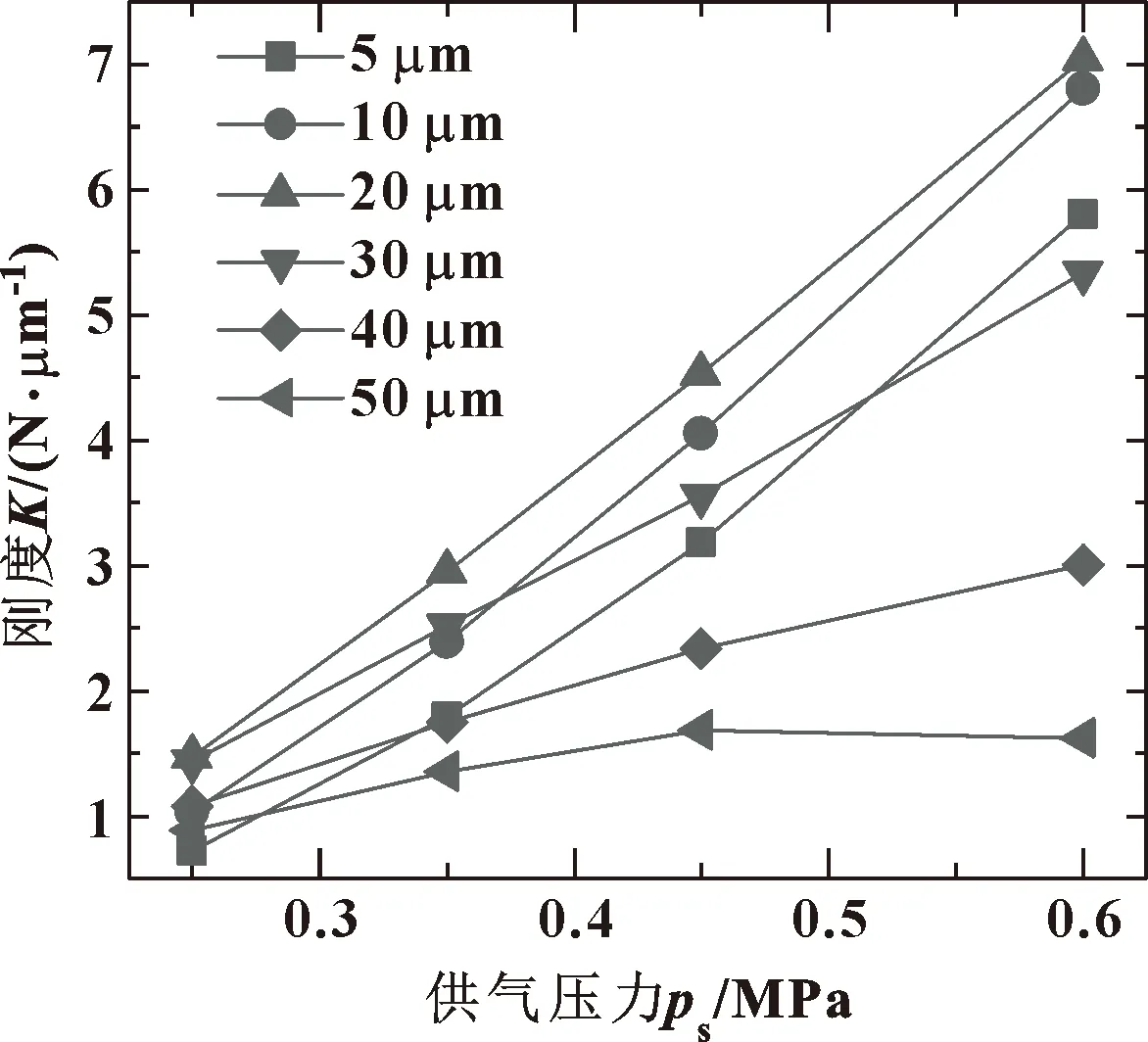
图7 不同气膜厚度下刚度随供气压力变化
图8给出了轴承承载力随供气压力的变化。可以看出,随着供气压力的增大,承载力近似呈线性增大[7]。这是因为,随着供气压力的增大,气膜上相同位置处的压力增大(如图5所示),因此承载力增大。因此可以通过增大供气压力的方法提高承载力,但是供气压力太大会造成气锤振动现象[14],因此应该在保证轴承稳定工作的前提下,尽可能选择较大的供气压力。

图8 不同气膜厚度下承载力随供气压力变化
2.2 气膜厚度对轴承压力分布、刚度和承载力的影响
2.2.1 气膜压力场分布变化
从图5中可以看出轴承压力分布随气膜厚度的变化规律相同:随着气膜厚度的增大,轴承上相同位置处的压力在不断减小。为了进一步分析压力沿径向变化情况,沿2个供气孔中心所在位置取一条压力分布线,如图9所示。
从图9中可以看出,气膜厚度不同时,压力沿径向的变化规律不同。气膜厚度较小时(<20 μm),气膜压力朝内径和外径方向上都近似呈直线下降,小孔附近压力梯度较大。但当气膜间隙较大时(>20 μm),压力在小孔周围先骤降,然后又快速升高到大气压力以上,最后再逐渐降低至大气压力,且压力下降幅度随着气膜厚度的增大而增大。气膜厚度为40和50 μm时,气体流出小孔时压力甚至降为负压,在不同气膜厚度和不同供气压力下压力最小点的位置不变[15]。这是因为供气孔和气膜连接截面上流通面积突然减小,在流过该截面后流通面积又逐渐增大。随着气膜厚度的增加,截面变化程度越来越大,使得供气孔处的流速增大,压力出现骤降。

图9 不同气膜厚度下气膜压力分布随供气压力变化
2.2.2 气膜刚度和承载力大小变化
图10给出了不同供气压力下刚度随气膜厚度的变化曲线。可以看出,不同供气压力下刚度随气膜厚度变化的规律相似。随着气膜厚度的增加,不同供气压力下的轴承刚度都呈现先增大后减小的趋势,每个供气压力下存在一个最佳气膜厚度,使得刚度最大[16]。

图10 不同供气压力下刚度随气膜厚度变化
图11给出了轴承承载力随气膜厚度的变化。可以看出,在相同供气压力下,随着气膜厚度的增大,承载力不断下降。结合压力分布进行分析,气膜厚度增大时,相同位置处的压力减小,因此承载力下降。因此可以减小气膜厚度以增大承载力,同时考虑到轴承的静态刚度,应该将气膜间隙控制在刚度下降之前。

图11 不同供气压力下承载力随气膜厚度变化
根据以上压力分布曲线,选择供气压力0.6 MPa时,气膜厚度分别为5、20和50 μm时气膜入口处的速度矢量图和流线图进行分析。
从图12中可以看出,在气膜厚度不同时,气体的流动状态有很大差异。当气膜厚度为5 μm时,由于气膜厚度小,流通面积急剧减小[17],此时中间气体的速度方向开始发生变化,产生了回流和漩涡,进入气膜的速度在2~6.25 m/s之间。四周的气体受到中间气体的影响,方向有一定变化。当气膜厚度为20和50 μm时,由于流通面积大大增加,小孔中没有明显的回流和漩涡现象,进入气膜的气体速度分别在40~60 m/s和100~150 m/s之间。
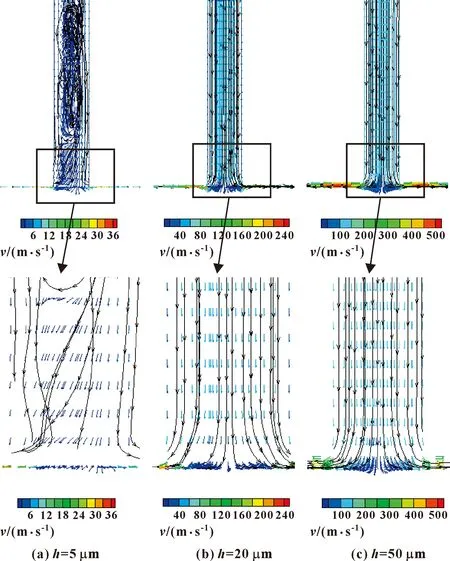
图12 气膜厚度为5、20和50 μm时气膜入口处的速度矢量图和流线图
图13示出了气膜厚度为5、20和50 μm时气膜入口处的速度矢量和压力分布。由小孔附近的速度矢量图可知,在气膜厚度为5 μm时,气体流出小孔后速度持续降低,在气膜入口处速度最大,约18 m/s;在气膜厚度为20 μm时,气体流出小孔后速度有短暂上升,之后降低,最大速度约为240 m/s;在气膜厚度为50 μm时,气体流出小孔后速度上升的区域比20 μm时更大,最大速度在500 m/s左右,超过音速。
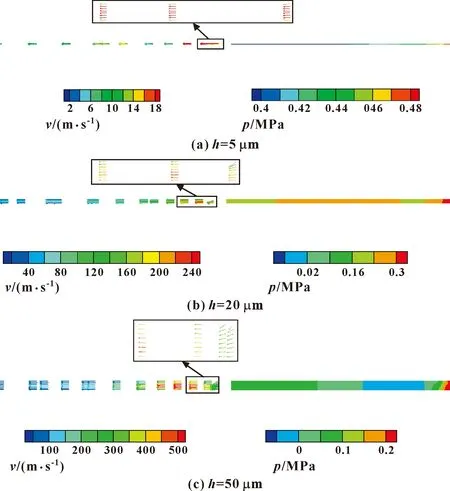
图13 气膜厚度为5、20和50 μm时气膜入口处的速度矢量和压力分布对比
由图13中压力分布可知,在气膜厚度为5 μm时,在气膜的气体流动方向上,压力由进口处的0.48 MPa逐渐降低;在气膜厚度为20 μm时,沿气体流动方向,压力先减小后升高,之后再持续降低至环境压力;在气膜厚度为50 μm时,在气膜的气体流动方向上,压力同样先减小再升高,之后再一直减小到出口,但在接近入口处压力降低范围比20 μm时更大,最低压力达到负压时比20 μm时更低,约为-0.04 MPa。
对比图13中小孔附近的速度矢量和压力分布可得:在速度最小的地方压力达到最大,速度最大的地方压力最小[16],这是实际的喉部位置。在出现压力骤降现象时,压力损失增大[18],这种压力损失一部分转化为气体的动能,提高气体的运动速度,另一部分是由于气流方向改变和节面突变而产生的局部压力损失。且在压力回升区域可以看出随着气膜厚度的增大,回升幅度随之减小[19]。在超音速区域,压力下降极大同时承载能力大幅下降,因此应该合理设计轴承的参数,选择合适的供气压力,避免超音速区域的出现。
为了验证该模型和方法的准确性,根据文献[20]对一个内径20 mm、外径38 mm的单排孔静压气体止推轴承利用FLUENT进行计算,并把计算结果与文献实验结果进行对比,如图14所示。可以看出两者吻合较好,因此证明了文中模型和方法用于气体轴承的模拟是有效的。

图14 数值模拟与文献实验结果对比
3 结论
(1)环形节流静压止推气体轴承上的压力分布随着供气压力的增大而增大;当气膜厚度较小时,压力分布符合雷诺方程,当气膜厚度较大时,在小孔附近产生激波而出现压力骤减现象。在气膜中速度最小的地方压力达到最大,速度最大的地方压力最小。
(2)在供气压力一定时,随着气膜厚度的增大,刚度先增大后减小,存在最大刚度值。
(3)环形节流静压止推气体轴承的承载力随着供气压力的增大而增大,随着气膜厚度的增大而降低。因此减小气膜厚度可增大承载力,但同时考虑到静态刚度,气膜厚度应合理控制以避免出现超音速流动。

