高速低温两相机械密封膜压特性研究*

曹生照 涂 霆 郝木明 于 博 姜绪强 任宝杰 李勇凡

(1.中国石油大学(华东)新能源学院 山东青岛 266580；2.北京航天动力研究所 北京 100076；3.东营海森密封技术有限责任公司 山东东营 257067)

接触式机械密封因结构相对简单、密封性良好而被广泛应用于液体火箭发动机涡轮泵轴端[1]，以阻隔高压密封介质向高温燃烧室的泄漏。作为火箭动力系统的核心零部件，接触式机械密封稳定可靠运行是保障火箭成功发射的重要因素件[2]。

某涡轮泵机械密封结构如图1所示，其主要由动环、静环、金属波纹管、密封壳体等组成。由于涡轮泵高速运转及介质环境的特殊性，影响机械密封运行稳定性的因素众多，研究人员对其进行深入研究。陈鹏飞等[3]研究了静环振动对涡轮泵密封腔内流体的激励作用，并分析了对密封失效的影响规律。张树强等[4]建立了涡轮泵机械密封稳态传热模型，研究了端面比压、回流流量及密封环材质对密封环温度场及热载变形影响。尹源等人[5]对涡轮泵机械密封润滑与摩擦磨损机制进行了综述，指出混合润滑和边界润滑问题的解决可实现对小膜厚运行工况的准确解释。张峰等人[6]分析了某涡轮泵试车时机械密封发生的故障，指出高速摩擦副热量的集聚使密封端面液相介质汽化为故障出现的主要原因。郭军刚等[7]分析了超高速涡轮泵机械密封工作特性，指出超高速运转时摩擦热的剧烈生成可导致密封环失稳。可见已有较多学者对影响涡轮泵机械密封运行稳定的因素进行了多方面研究，且指出高速运转时密封液相介质的汽化[6-8]为影响密封可靠性的重要因素。但上述文献均未对高速工况、低温易相变密封介质环境下的两相机械密封流动现象及膜压性能进行研究，而因介质相变造成的密封性能改变往往可导致密封环相变失稳，这也是导致机械密封失效的主要原因之一[9-10]。

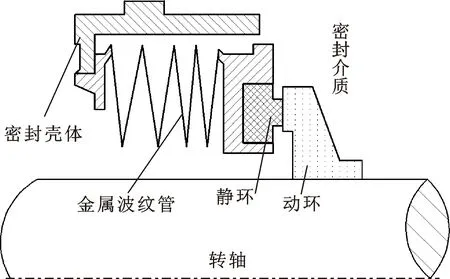
图1 涡轮泵用机械密封结构简图

鉴于此，本文作者建立了适用于接触式平端面机械密封的二维轴对称相变模型，计入高速离心惯性效应与摩擦热影响，以低温液氧为密封介质，在流体润滑状态下分析了流体膜相变流动及高速运转时离心惯性效应对流体膜相变影响机制，着重探究各因素对密封端面膜压系数影响规律，为高速、低温火箭发动机涡轮泵机械密封优化提升提供指导。

1 理论模型

由于机械密封端面间隙液膜相变过程较为复杂，且存在跨尺度质量、动量以及能量传递，为便于求解分析，基于均相流模型及流体润滑理论可作以下假设：

(1) 密封动静环端面为理想光滑的，不考虑表面粗糙度影响，且完全对中。对接触式机械密封，虽然其多工作于混合润滑而非流体润滑状态[11]，但由于流体膜两相流动的复杂性，对密封间隙的相变研究仍多忽略粗糙表面接触影响[9-10]，且文中重点在于研究密封端面液膜在高速工况下所表现的两相流特性及对密封性能影响，故延续了假设(1)。

(2) 密封端面流体为稳态层流流动，忽略体积力影响，计入迁移惯性项而忽略当地惯性项影响，且在膜厚z方向与周向不计各物理量的变化，即各物理量仅为径向坐标r的函数，密封端面流体域如图2所示。

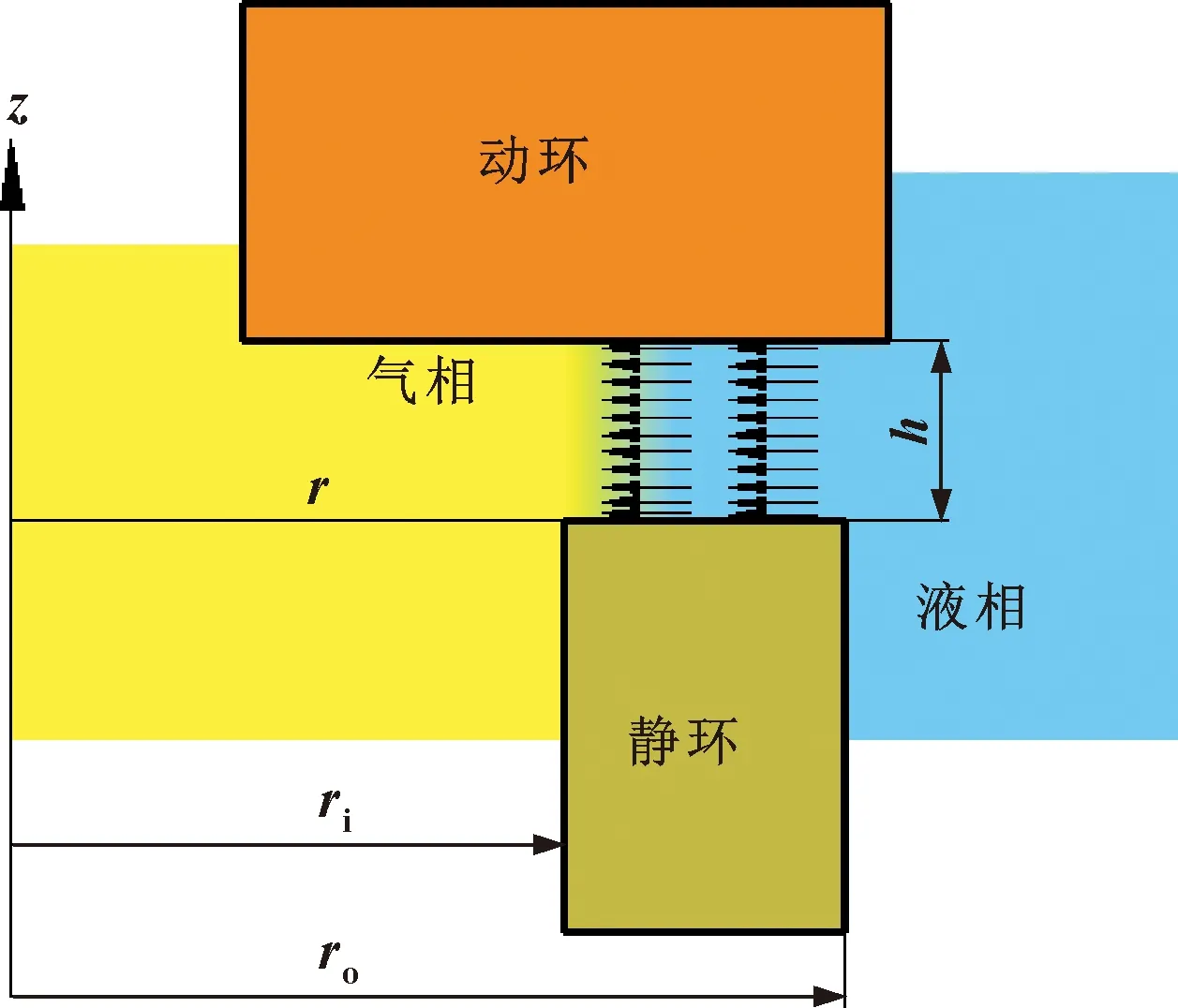
图2 计算流体域模型

(3) 密封端面流体膜为纯物质液相与相应气相的均质混合物，均相流体物性参数由容积含相率[12]加权确定，均相流体密度ρ、均相流体黏度μ、均相流体热导率k以及均相流体普朗特数Pr等物性参数按式(1)计算。

(1)

式中：αL、αG分别为容积含液率和容积含气率，且满足αL+αG=1；ρL、ρG、μL、μG、kL、kG、PrL、PrG分别为液相密度与气相密度、液相动力黏度与气相动力黏度、液相热导率与气相热导率、液相普朗特数与气相普朗特数。

(4) 液相为不可压缩流体，相变气相满足以维里方程表示的实际气体状态方程，其他气液相物性参数皆为温度的函数，计算时直接从物性参数数据库软件REFPROP调取。

1.1 均相流体控制方程

基于前述均相流体假设，描述纯物质液相与气相质量守恒的连续性方程[13]为

(2)

式中：V为均相流体速度矢量，在极坐标系中表示为V=(Vr,Vθ,Vz)；ψ为质量源项，表征相变过程中液相与气相之间的传质速率，按文献[11]计算。

由式(1)，将气液相连续性方程(2)相加，均相流体连续性方程为

∇·(ρV)=0

(3)

均相流体动量方程[13]为

∇·(ρVV)=ρF+∇·P

(4)

式中：F为单位体积质量力；P为二阶应力张量。

均相流体能量方程[13]为

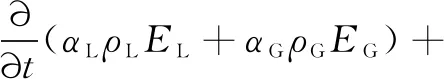
αGρGEG)V]=∇·(k∇T)+∇·(P·V)+ρF·V+q

(5)

式中：EL=UL+V2/2、EG=UG+V2/2分别为单位质量液相总能量与气相总能量；UL、UG分别为单位质量液相内能与气相内能；V为均相流体速度标量；T为流体膜温度；q为单位体积其他热源。

对不可压缩液相，内能微分表达式为

dUL=cLdT

(6)

式中：cL为液相定容比热容。

对相变气相，以维里方程表示其实际气体状态：

(7)

式中：Z为实际气体压缩因子；υG为气相比体积；RG为气体常数；B为介质第二维里系数。

则气相内能微分表达式为

(8)

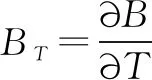
将式(6)、(8)代入式(5)，稳态流动时均相能量方程可化为

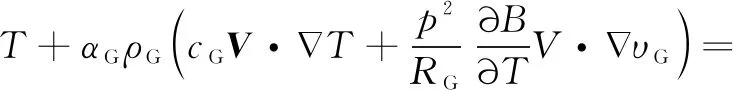
-p∇·V+Φ+∇·(k∇T)+(UG-UL)ψ+q

(9)

式中：Φ表示黏性耗散热源，其全部转化为热能。

1.2 极坐标相变控制方程

由假设(2)、(3)，对方程(4)化简求解，计入迁移离心惯性项并由机械密封端面特定边界条件限制的密封端面流体速度计算式[14]为

(10)

式中：ω=2πn/60，n为动环转速。

将式(10)代入方程(3)，并在膜厚方向积分，且由流体膜轴对称假设，可得极坐标轴对称形式均相Reynolds方程为

(11)

式中：Iω=ω2表示计入离心惯性效应影响，而Iω=0表示忽略离心惯性效应影响。

按文献[11]中方法化简方程(2)并相加求和，可得极坐标轴对称形式均相传质控制方程为

(12)

将式(10)代入方程(9)，并在膜厚方向积分，耗散热源项Φ按文献[14]计算，可得极坐标轴对称形式均相能量方程为

(13)

式中：QΨ、Qρ、QB、QΦ、Qα分别表示相变热源项、气相压缩(膨胀)热源项、实际气体影响热源项、黏性耗散热源项以及对流给热热源项，由式(14)计算。

(14)

式中：Qα中Tw,r、Tw,s分别为密封动、静环端面平均温度；αr、αs分别为端面流体膜与密封动、静环给热系数，按文献[15]计算。

1.3 性能参数定义

机械密封端面膜压系数反映了在被密封流体压差作用下，密封端面承载能力的大小，处于不同相态的机械密封其膜压系数有较大不同，且可根据膜压系数判断密封所处稳定状态[16]。因此文中主要研究各参数对膜压系数影响关系。膜压系数的定义为

(15)

1.4 数值求解

文中研究对象为如图2所示的接触式机械密封端面流体膜，采用基于有限元方法的数值软件COMSOL Multiphysics对式(11)—(14)组成的相变控制方程组离散求解；在COMSOL一维轴对称模式下绘制计算流体域，径向网格采用等间距划分，以偏微分接口系数形偏微分方程模块输入方程(11)—(13)所对应方程系数并设定内、外径边界条件；由于密封端面流体相变为具有强耦合的多物理问题，故选用全耦合求解器实现方程的迭代求解，求解相对容差设置为10-6。

1.5 模型验证

为验证相变方程组正确性，在高温热水介质条件下与LEBECK[8]改进的间断沸腾模型对比，密封面几何与工况参数详见文献[8]，计算结果如图3所示。可见两者压力与温度值均仅有较小偏差，而出现差异的原因为：文献[10]考虑了表面粗糙度影响(但文献分析表明此工况下粗糙度影响较小)且端面摩擦生热完全进入密封环并与环境介质对流换热，而文中计算时仅部分热量进入密封端面，传热模型之间的差异为计算结果出现偏差的主要因素。由于此工况转速较低，故文中忽略离心惯性效应与计入离心惯性效应计算结果相差微小，且图3所示为计入离心惯性效应计算结果。

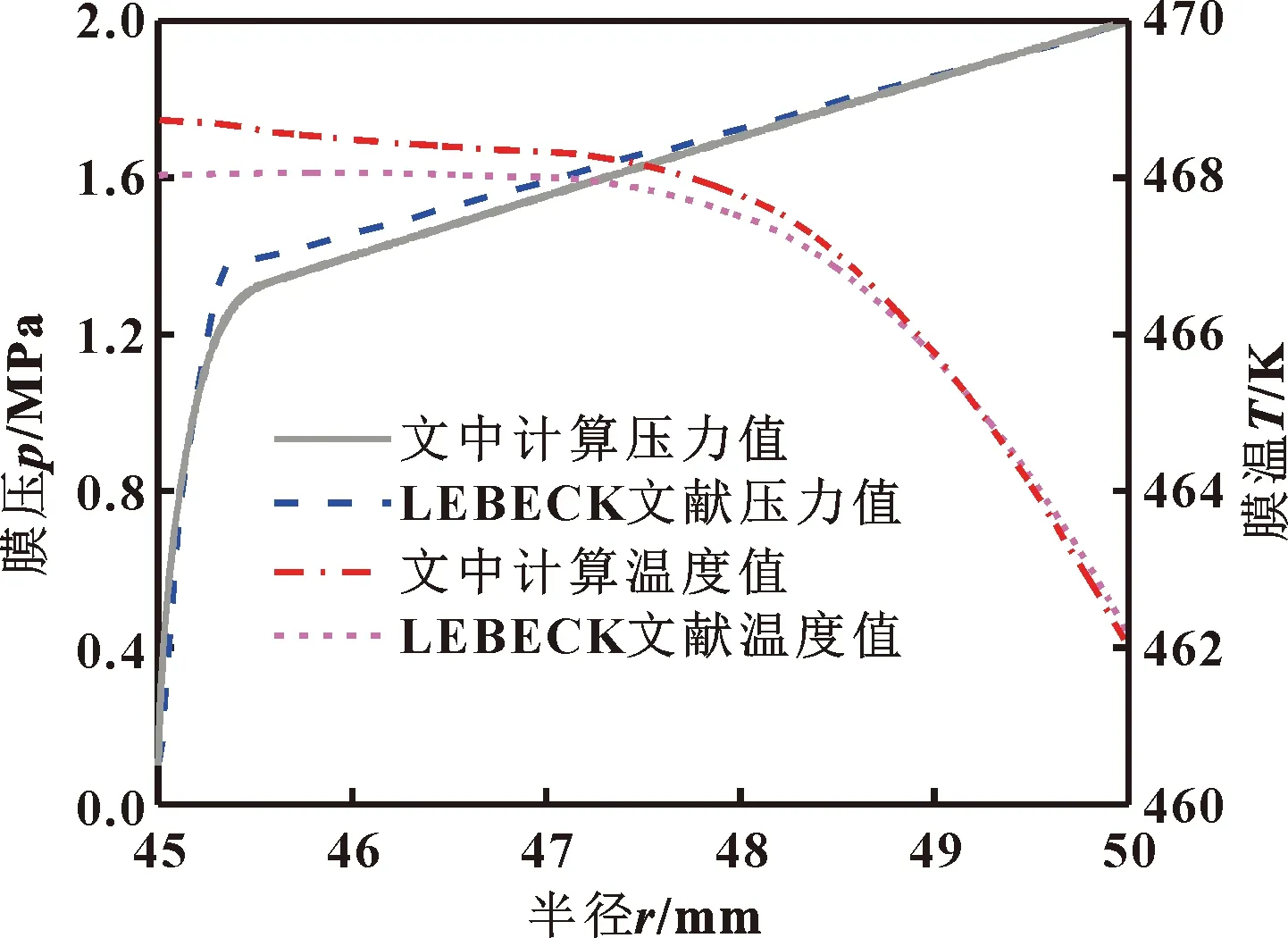
图3 模型验证

2 结果及分析

文中研究所用外压式机械密封基本结构与工况参数为：内径ri=34.5 mm，外径ro=41.5 mm，膜厚h=5 μm，转速n=2×104r/min，内径压力pi=0.1 MPa，外径压力po=1.5 MPa，外径温度To=77.5 K，外径液相体积分数αLo=1，模型分析时若无其他说明，均按基本参数计算。

2.1 离心惯性效应对相变特性影响分析

图4所示为不同转速时密封端面流体膜压力、温度、液相体积分数分布。

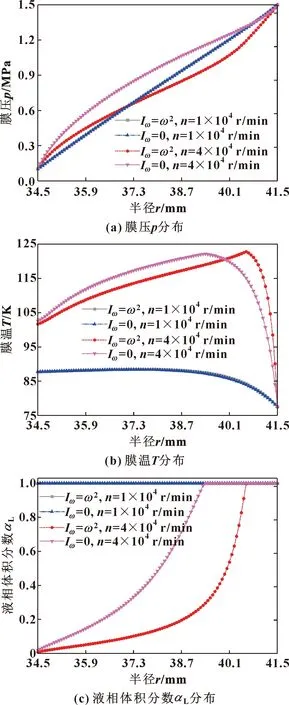
图4 离心惯性效应对密封相变影响

可见在转速1×104r/min时，因流体黏性耗散生热较小，故端面温升较低，Iω=ω2与Iω=0均未有相态转变，流体膜压力由外径入口值近似线性递减至内径出口值，由于液相密度为定值，且此时转速较低，故Iω=ω2与Iω=0计算值无明显差异。而转速为4×104r/min时，转速的大幅提升使得密封动、静环端面间流体速度梯度增大，黏性耗散热大幅增加而使温度明显升高，如图4(b)所示，但Iω=ω2与Iω=0温度差异较小。由图4(a)可见，相较于转速1×104r/min时，转速4×104r/min且Iω=0时膜压普遍增大，而Iω=ω2时膜压既有减小也有增大，且Iω=0膜压明显大于Iω=ω2时。分析原因为：在均相Reynolds方程中，离心惯性源项为负值，在保持物性参数与工况参数不变时，离心惯性项的计入将使得膜压p减小，且转速越大，由离心惯性效应引起的压力降越大；而在膜温近似不变时，压力的大幅降低相当程度促进了流体相变的发生，如图4(c)所示。

由于离心惯性效应由密度、黏度沿径向变化梯度所引起，而两相状态时均相流体物性参数由相体积分数加权确定，故相变的发生将使离心惯性效应对密封性能影响增强，且随转速增大而愈加明显。当相变极大发生时，均相流体黏度的减小会降低端面的润滑性能，且相变发生若处于不稳定状态，可能发生相态失稳，因此在高速涡轮泵机械密封设计时，应详加考虑因离心惯性效应及相变对密封性能的综合影响。

2.2 膜压系数研究

图5所示为计算模型不同时，密封端面膜压系数随介质温度变化，其中T=To为按等温模型且Iω=ω2计算，而Iω=0与Iω=ω2均为非等温模型计算。可见在T=To时，po=0.5 MPa(对应饱和温度为108.8 K)与po=3.0 MPa(对应饱和温度为141.7 K)膜压系数在温度较低时近似相等，约为0.53，与顾永泉[16]液相机械密封计算值0.52较相一致。随介质温度升高，两介质压力所对应膜压系数均缓慢上升至最大值，其后又在饱和温度点处急剧下降并趋于稳定。分析原因为：介质温度的升高增大了端面流体相变发生区域，使膜压曲线上凸，承载能力增强；但需注意的是，膜压系数最大处虽有着较高的承载力但也有着较差的稳定性，当介质温度略有波动时，膜压的大幅变化可诱发相变失稳；由于较低的介质压力使得在温度较低时相变就已发生，因此在一定温度范围内，po=0.5 MPa膜压系数大于po=3.0 MPa时。

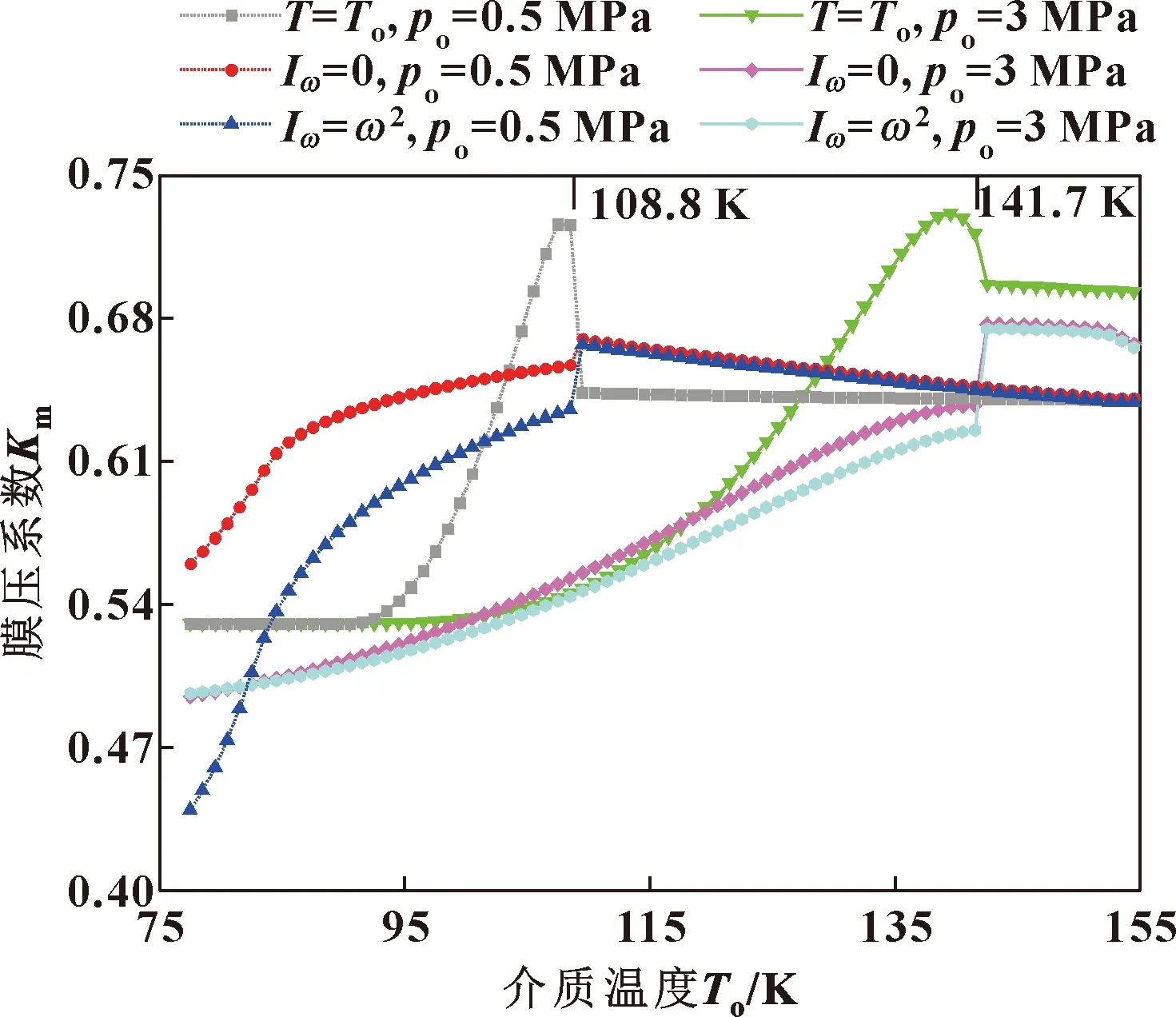
图5 计算模型对比

由于离心惯性效应的影响使得膜压有所降低，因此Iω=ω2时膜压系数始终小于Iω=0时，但两者膜压系数随介质温度升高均先平稳上升而后在饱和温度点处骤然增大，其后又略有下降，但幅度较小；当介质温度大于入口压力对应饱和温度时，密封流体将呈气相进入，此时因离心惯性效应引起的膜压变化较为微小，因此Iω=ω2与Iω=0时膜压系数近乎相等。对比3种模型计算结果可知，无论端面流体呈何种相态，流体膜温度的变化均会影响膜压系数而改变流体承载能力，离心惯性效应的影响会使膜压系数有所减小。

图6所示为Iω=ω2时介质压力对膜压系数的影响。可见受离心惯性效应与相变发生综合影响，不同压力时的膜压系数在介质温度较低时变化较为不规则。取最小计算介质温度时，po=0.5 MPa时膜压系数约为0.44，而其他压力时膜压系数相差不大，均近似为0.5，且可见po=0.5 MPa与po=1.0 MPa时膜压系数与其他压力所对应膜压系数出现交叉。分析原因为：在流体温度较低时，液氧介质所对应饱和蒸气压较小，相变的发生虽使流体膜压力有所增大，但相变所影响的物性参数径向梯度变化使得离心惯性效应影响增强，综合表现为膜压系数减小，承载能力下降。当介质温度约大于90 K时，可见介质压力越小，膜压系数越大，不同介质压力时膜压系数随介质温度变化趋势总体一致，即先缓慢增大，在饱和温度值处发生突增，其后缓慢减小或先略有增大后缓慢减小；与低介质温度时较类似的是，除po=0.5 MPa时外，其他介质压力所对应膜压系数在介质温度高于一定值后相差较小，约为0.67；由于气相介质黏度随温度升高而略有增大，因此在介质温度大于入口压力饱和温度值时，po=0.5 MPa时膜压系数近似直线下降。

绘制膜压系数分界线如图6所示。可见临界点处膜压系数随介质压力增大而有所减小，且由于低介质温度时不同介质压力下的膜压系数相差较小，即膜压系数随介质温度变化率随介质压力增大而减小，这表明高介质压力时介质温度的轻微波动有着较小的膜压系数改变量，即密封稳定性增强。

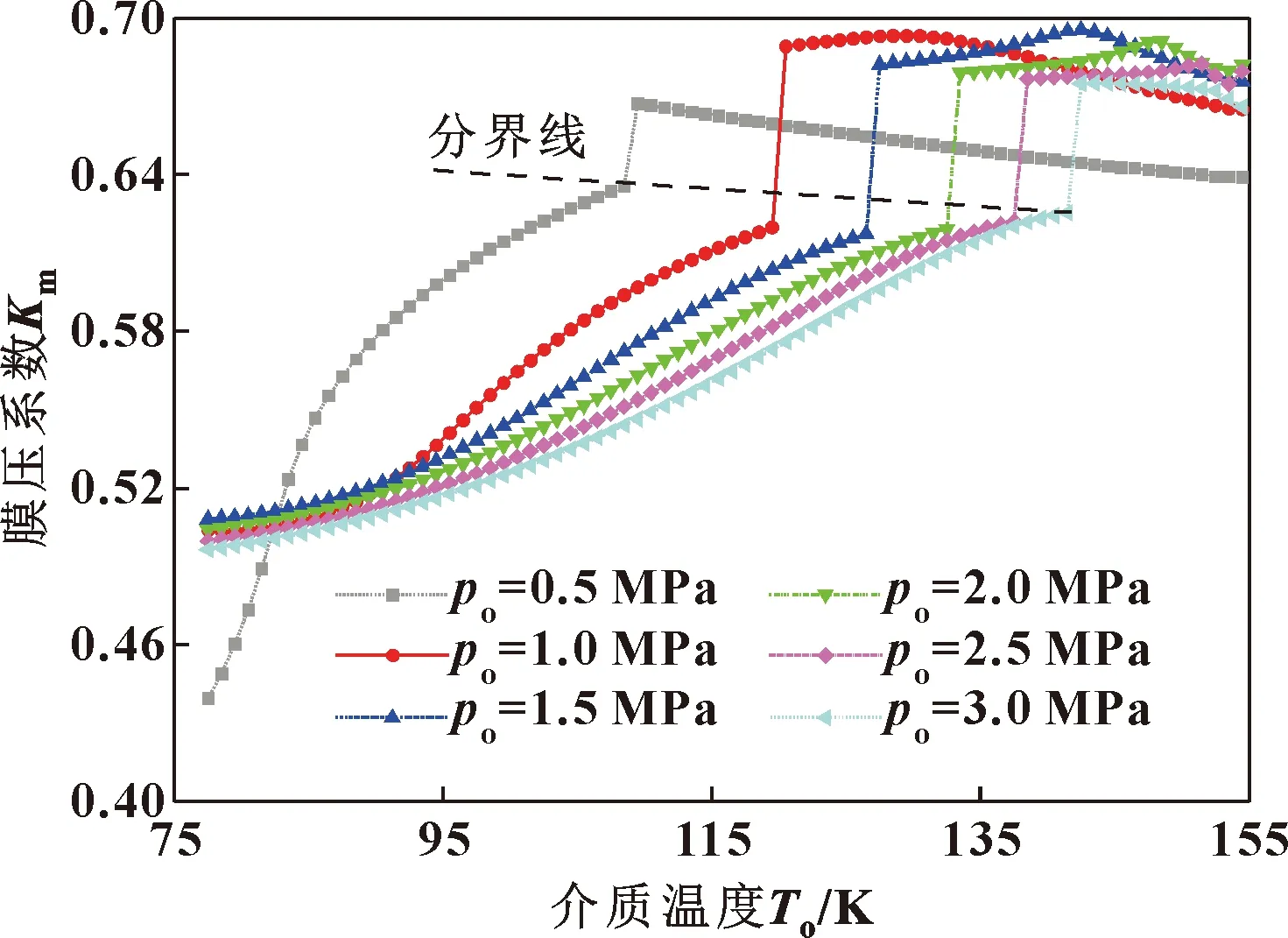
图6 介质压力对膜压系数影响

图7所示为Iω=ω2时转速对膜压系数的影响。可见在介质温度低于饱和温度值时，不同转速所对应膜压系数相差较小，但在一定温度区间内也有转速越高膜压系数越大趋势。分析原因为：转速越大，密封端面流体黏性剪切耗散热越多，相应温升越高，即相变程度增大，可使膜压增加；但由于离心惯性效应影响随转速增加而增强，相应使膜压又有所减小，在两者综合作用下，转速对膜压系数影响较弱，且表明两相机械密封在变转速启动时具有较强的稳定性。当介质温度高于饱和温度值时，密封流体已全为气相，而气相介质由外径高压泄漏至低压的过程中将主要由于膨胀吸热而使端面温度有所降低；由于转速越小，黏性耗散热生成越少，端面温度梯度下降将越大，在热致物性参数改变与离心惯性效应综合影响下，转速越高，膜压系数越大，即承载能力越强。

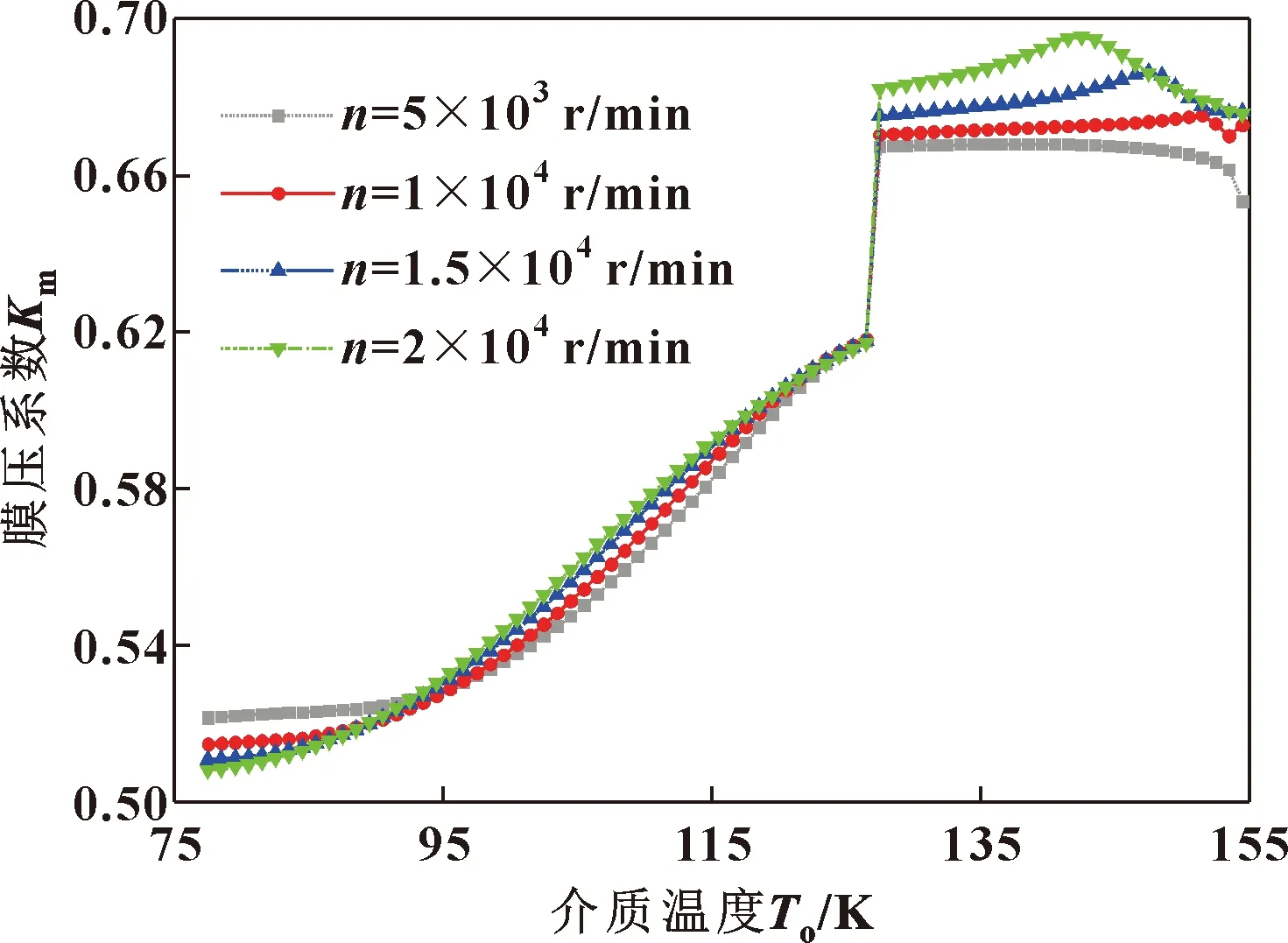
图7 转速对膜压系数影响

图8所示为Iω=ω2时膜厚对膜压系数的影响。可见当膜厚大幅度变化时，膜压系数随介质温度升高呈现出不同规律。在h≤1.5 μm时，膜压系数在介质温度低于饱和温度点内近似线性递减，而后在饱和温度点处减小速率有所增大，且当介质温度大于饱和温度值后膜压系数继续减小。膜厚为0.5、1.0、1.5 μm时膜压系数最大值均在最小计算介质温度值处取得，分别为0.681、0.688、0.705。而当膜厚为2.0与2.5 μm时，膜压系数曲线均先快速增大，并在一定温度值处达到最大值，其后缓慢下降并在饱和温度点处发生骤降，且可见在计算膜厚范围内，当前膜厚下膜压系数有最大值，分别为0.748、0.746，表明此时有较强的承载能力，且由于流体膜厚相对较小，故密封性能较优，但有着较差的运行稳定性。在h≥3.0 μm时，膜压曲线随介质温度升高均先缓慢增大，并在饱和温度点处突增，且饱和温度值处膜压系数随膜厚增大而有所减小。这与介质温度低于饱和温度值时相一致，即膜厚越小，膜压系数越大，承载能力越强，这是由于较小的流体膜厚更易诱发相变而使膜压增大。当膜厚为3.0～4.0 μm 时，膜压系数最大值均在饱和温度值处取得，而当膜厚为4.5与5.0 μm时，在介质温度高于饱和温度值后，膜压系数先略有增加，其后又略有减小，呈抛物线型变化，但当介质温度临近最大计算温度值时，不同膜厚时膜压系数近乎相等。

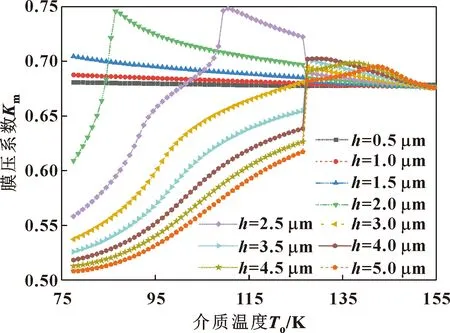
图8 膜厚对膜压系数影响

3 结论

(1)离心惯性效应使外压式机械密封流体膜压力减小，相变程度增大，但对温度影响较小；由于相变使得均相流体物性参数发生改变，因此也会加强离心惯性效应影响。

(2)等温模型膜压系数计算值随介质温度变化存在明显峰值，膜压系数最大处承载能力虽强但密封稳定性较差；非等温模型时，膜压系数随介质温度变化无明显稳定区间，介质温度的轻微波动将使膜压系数发生改变，而不利于密封的稳定运行。

(3)在介质压力与温度皆较低时，相变的发生可使膜压增大，但离心惯性效应的增强反而使膜压系数降低；在介质温度大于90 K时，随介质压力增大，膜压系数减小且随介质温度变化梯度降低，表明密封稳定性增强；受离心惯性效应与相变发生综合影响，转速的增加对两相机械密封膜压系数影响较弱。

(4)当膜厚h<1.5 μm时，膜压系数随介质温度升高而有所减小；当2.0 μm