改进直通滤波SAC-IA粗配准算法
宫德宁,吴琳娜,李荣华,卢祺
(1.大连交通大学 机械工程学院,辽宁 大连 116028;2.上海宇航系统研究所,上海 201109)
随着航天技术的飞速发展,空间在轨服务成为当前亟需技术,主要包括辅助变轨、碎片移除、在轨燃料加注与延寿、在轨装配和在轨维修等.空间目标三维重建是空间在轨服务的关键,三维重建技术主要包括可见光序列图像和激光雷达方法.Yingying Gu[1]通过单目相机测量,提出了一种在复杂光照条件下可以稳定提取目标图像投影角度的图像处理方法.刘玉[2]验证激光雷达的航天器相对位姿测量技术方法合理可行,测量精度高,可满足近距离操控中相对导航任务需求,对国内后续开展工程应具有较大参考价值.尹芳[3]针对激光3D点云数据跟踪配准中产生的累积误差问题,提出了位姿图优化的SLAM技术框架的方法.点云数据配准是空间目标三维重建必要途径,准确的点云配准可以提高三维重建精度.
点云配准分为粗配准[4〗和精配准[5].粗配准也叫初始配准,用于处理两幅未知点云位姿信息,为精配准提供良好的初值.近年来为了提高配准精度,越来越多的学者开始研究粗配准算法.Rusu[6]提出了计算点云特征描述的子方法,描述了中心点与其领域范围点之间的空间差异,形成点特征直方图(Point Feature Histograms,PFH).R.B.Rusueta[7]提出了一种基于FPFH特征的配准算法,该算法不仅提高了点云配准精度,也显著性提高了点云配准的效率.随着配准算法的进一步研究,NDT算法[8]、3DSC算法[9]和4PCS算法[10]开始得到广泛应用.Chen[11]首次在点云配准中运用RANSAC算法,继而Rusu[6]通过快速点特征直方图(Fast Point Feature Histograms,FPFH)描述子和RANSAC原理,提出了SAC-IA(Sample Consensus Initial Alignment)算法.
利用NDT、3DSC、4PCS和FPFH等传统算法实现了点云的粗配准,对部分点云数据能够得到较好的结果,为精确配准提供较好的初始旋转矩阵,但对于卫星点云等平面特征多且特征单一的特殊点云模型,容易产生异部分误匹配,导致粗配准失败.针对以上问题,本文提出改进直通滤波SAC-IA粗配准算法,首先对点云数据处理时,先需要进行离群点与噪声的去除;其次采用PCA算法计算点云数据中心点,去除均值,得到协方差矩阵,从而得出特征值以及特征向量;然后特征向量方向为主成分方向规定成分方向为Z轴进行坐标变换,再对Z轴方向进行直通滤波,保留卫星主体部分,去除太阳能帆板,再进行主体部分下采样滤波,能有效提高配准精度;最后计算2个待配准点云的法向量,使用Kd-Tree树结构对点云的FPFH特征进行加速计算,得到目标点云和待配准点云的FPFH特征.再根据2个点云相似的FPFH特征,使用SAC-IA算法求解变换矩阵,同时对前期PCA算法处理后的点云进行逆变换,求累积矩阵变换,完成点云粗配准,具体点云粗配准路线见图1.

图1 配准路线图
1 改进点云直通滤波
根据真实卫星尺寸进行1∶1三维建模,经MeshLab软件处理三维模型,生成卫星点云数据,最后在通过MATLAB对数据仿真,得到局部可视点云,仿真过程中加入噪点,模拟真实数据情况.在处理点云数据时,大多数需要通过滤波重采样来对点云进行预处理,在保留特征的前提下节省特征子计算时间,提高点云配准精度和时效性[12].考虑到卫星点云初始目标的太阳能帆板平面部分和目标点云卫星主体平面部分点云造成误匹配,为了得到准确的点对对应关系,本文首先去除点云离群点,然后采用PCA变换分析方法估算点云的法向信息,获得点云的三个主方向,获取质心,求得协方差矩阵,从而求解出矩阵的特征值和特征向量,特征向量即为主方向.接着校正主方向垂直,变换矩阵为M,对点云进行坐标变换,这样无论卫星在任何位姿下,都能准确地保留中主体部分.计算过程如下:
(1)求每个维度的平均值
(1)
(2)
(3)
式中:N是点云中点的总个数.
(2)求协方差矩阵以及对应的特征值、特征向量
(4)
Cλ=μλ
(5)

利用矩阵知识,求协防差矩阵C的特征值λ和相对应的特征向量μ,特征向量为主方向.
(3)用(1),(2)中获得的点云主方向和质心,将输入点云转换到原点位置,且主方向与坐标系Z轴方向重合.再进行点云直通滤波,如图2所示,因为卫星的点云主体宽度尺寸已知为A,所以直通滤波时选取滤波范围A,剔除两侧太阳板,保留卫星目标的主体部分,点云数据通过对主体点云进行下采样滤波处理,不仅提高了计算效率,而且能有效防止对应点对之间产生错误,提高准确率.
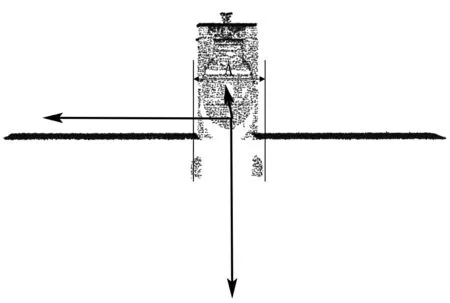
图2 改进点云滤波图
2 点云配准
在点云的初配准中,首先计算经过滤波处理卫星点云主体部分中每个点的FPFH,然后使用SAC-IA算法在目标点云中查找与待配准点云中具有相似FPFH特征的点,从这些相似点中构建对应点对应关系.计算旋转变换矩阵,旋转平移待配准点云完成配准.
FPFH是由PFH改进而来的,首先计算查询点与邻域点之间的关系,而不计算邻域点与邻域点之间的关系特征,接着再确定查询点与邻近点的理论复杂度.虽然FPFH没有对近邻点所有组合进行计算,可能会导致重要点对的丢失,但在进行权重和邻近点的重新计算过程中,降低了信息复杂度,增加了适用性,有效提升运算速率.
FPFH在计算Pq和其k邻域点Pk1~Pk5,构建每一个领域点的局部坐标系,分别计算出每个k领域点的四元组,获得特征直方图,不计算领域点与领域点之间的关系,得到简化的点特征直方图(Simple Point Feature Histograms, SPFH).如图3所示,分别以Pk1~Pk5作为目标点寻找其k邻域点并计算法向量、构建局部坐标系、获得Pq和其邻域点为目标点的SPFH.点Pq的FPFH特征计算公式为:
(6)
式中:Pq和Pk为相邻点;ωk是Pq和Pk的距离权重.
在式(6)中,以Pq和其邻域点Pk之间的距离作为权重.首先获取卫星点云全部点的简化特征直方图,接着通过点云的简化特征直方图与邻域点的SPFH值重新加权计算,最后得到卫星点云的快速点特征直方图,如图3所示.
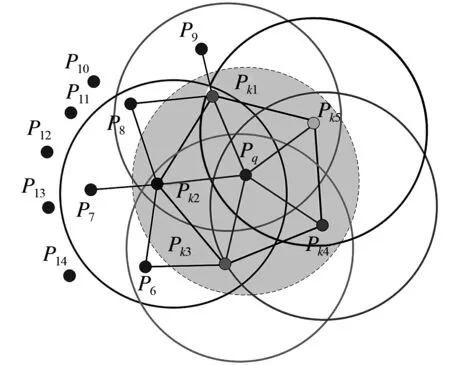
图3 FPFH计算原理图
计算完卫星主体部分特征描述子之后,通过采样一致性初始配准算法(Sample Consensus Initial Aligment)来寻找两幅卫星点云的对应点,从而得出旋转平移矩阵.具体步骤如下:
(1)从待配准点云A′中选取m(m>3)个采样点,规定采样点之间的最小距离,能保证采样点具有不同的快速点特征直方图特征.
(2)查找待配准卫星点云A′的点与目标卫星点云B′中的点具有相似的快速点特征直方图特征,选取相似特征的点云作为待配准点云与目标点云的对应点.
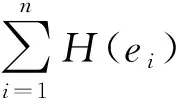
(7)
式中,ei为第i组对应点变换之后的距离差,L为预先给定值.
3 坐标变换
配准的结果不仅要从图像得出,也要从最后得出的平移 、旋转数据上体现,二者需要相辅相成,而坐标变换也是点云配准得到平移、旋转误差的重要途径.本文在求初始点云跟目标点云之间的变换经过了两次变换,首先是两幅点云的主成分方向变换,然后是经过变换后的点云配准变换,所以求取初始点云与目标点云之间的位姿变换需要对两次变换矩阵整体求逆变换,得到的矩阵是要求取的误差矩阵.具体流程如图4所示.

图4 矩阵变换流程图
其中点云A是初始点云,点云B是目标点云.最后配准过程输出结果是矩阵P.在矩阵变换过程中,符合下列计算规则,其中C,D,E为可逆的4×4阶矩阵:
(8)
(9)
(10)
如果CD=E,那么
(11)
在矩阵进行变换时,
CD=E⟹C=ED-
(12)
所以根据式(12)可以得出:
P=M×N×O-
(13)
4 结果与分析
本文实验平台配置如表1所示.
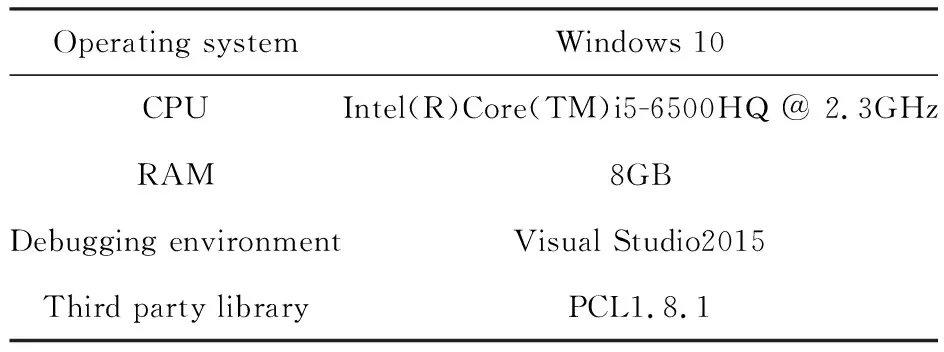
表1 系统环境配置
如图5所示,采用了一组仿真数据自旋4.979章动5.103 7章动角56.68的第0帧和第5帧两组可视点云进行实验,两组数据由于扫描数据时相机的站位不同,自身遮挡重叠部位点云数据无法显示,不能得到全部点云.图5中的原始点云数据有16 782个点,目标点云数据有19 054个点.

图5 输入点云模型
由于点云数据遮挡部分不同,形成的可视点云数据对应部分减少,增加配准难度,对效率和精度影响大.首先对点云进行主成分分析,接着对点云进行变换,最后对点云进行直通滤波,图6(a)为处理后的原始点数据,图6(b)为处理后的目标点云数据.

(a) 处理后的原始点云

(b) 处理后的目标点云图6 直通滤波处理后的结果
为了验证本文算法的有效性,跟传统的3DCS、4PSC、FPFH、NDT粗配准算法进行比较.通过对比配准前后点云模型在X、Y、Z轴的旋转误差和平移误差来判定配准精度,从而得出配准结果.为验证算法的有效性,控制其他阈值对配准结果的影响,对仿真数据进行相同的滤波,去除离群点,进行配准,并记录了不同点云配准方法完成卫星点云粗配准所需的时间和平移旋转误差,配准实验效果如图7所示.
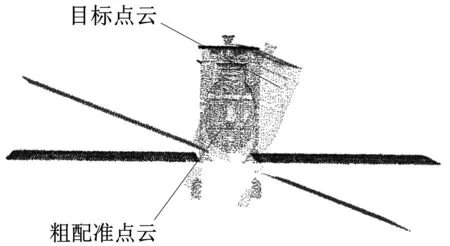
(a) 3DSC配准
在配准效率方面,通过点云配准所需要的时间来反应.实验数据如表2所示.
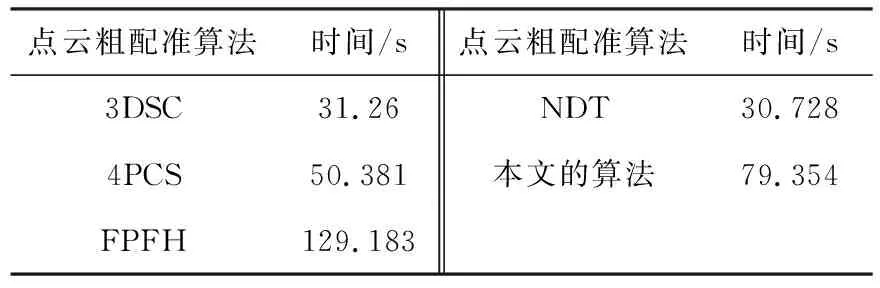
表2 配准时间表
在配准精度方面,通过不同坐标轴的旋转误差来反应,如表3和图8所示.
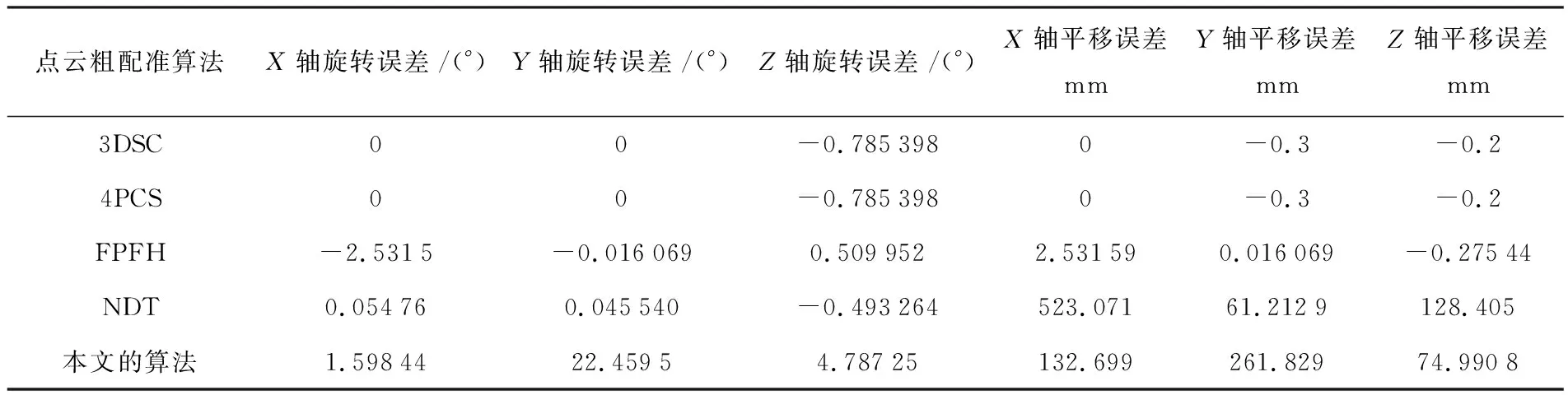
表3 误差记录表
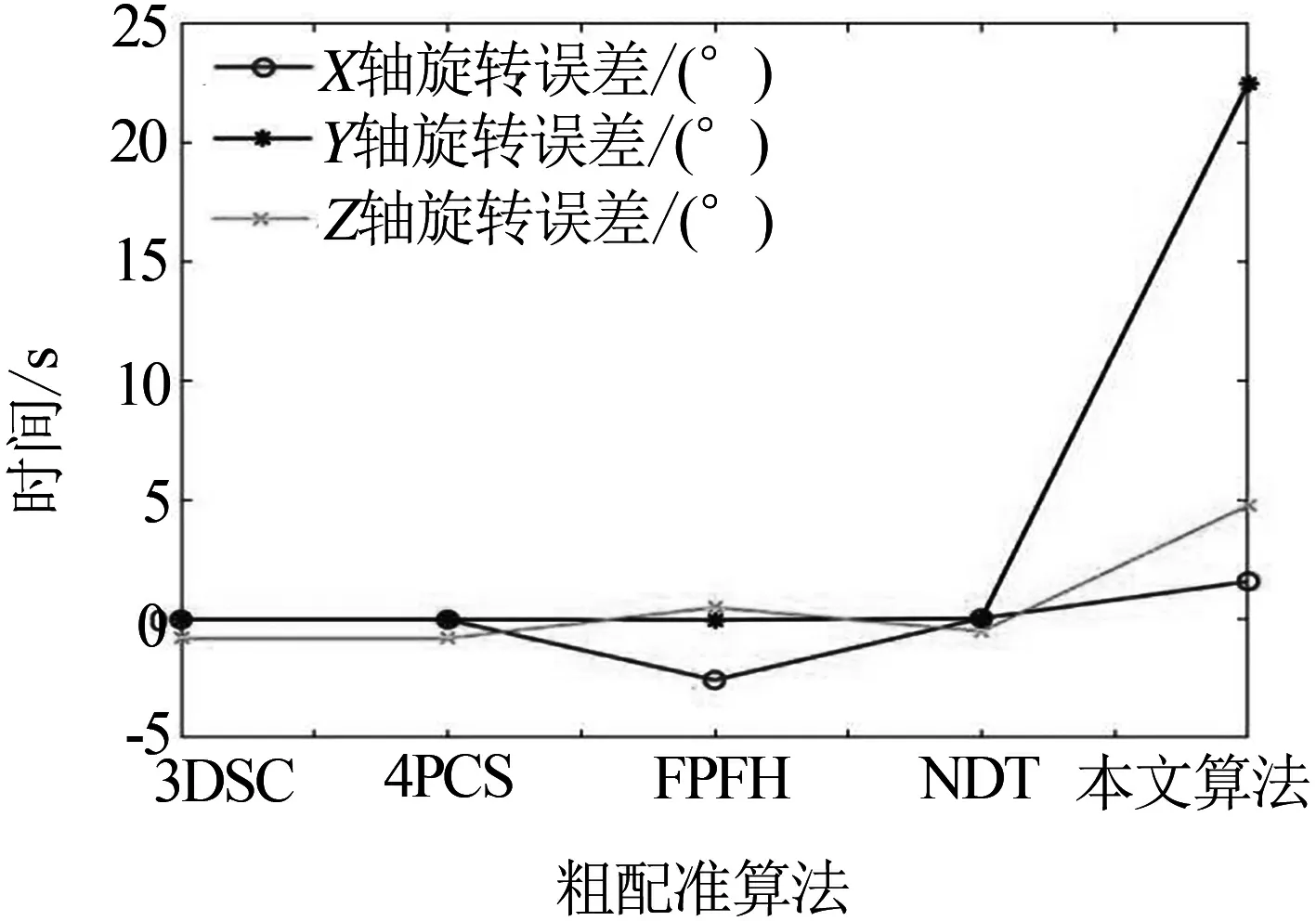
(a) 粗配准旋转误差
在基于局部特征的描述算法中3DSC的点云配准时间要明显小于FPFH,由于快速点特征直方图需要计算查询点与邻域点之间的关系,消耗时间长.3DSC需要计算出点云的曲面形状特征,增加了计算量,由于点云的数量多,计算查询点与领域点之间的关系消耗的时间要远大于计算出点云的曲面形状特征.卫星点云由于曲面特征少,平面特征较多导致3DSC计算形状特征配准失败;在基于全局特征的描述方法中4PCS需要计算两幅点云共面的四点基,然后依据放射性不变的原理,进行刚体变化,卫星模型由于其特征大多数是直面特征,导致计算时间短,配准失败;NDT计算正态分布是一个一次性的工作(初始化),不需要消耗大量代价计算最近邻搜索匹配点概率密度函数,在两幅图像采集之间的时间可以离线计算出来,配准效率高,但是精度低,受点云的模型影响大;本文提出的算法虽然在前期进行点云主成分分析和坐标变换时占用了时间,但是在后面配准过程中采用直通滤波后的点云数据,在保证足够配准所需的特征前提下,大大减少了点云的数量,去除部分相似特征部分,如图8所示,在不同算法的配准结果中,本文所提算法的配准效果最好,能提高效率和配准精度.由此可见,本文算法能够对卫星点云,可以实现高精度、高效率的点云粗配准.
5 结论
针对卫星目标的几何形状特殊、平面特征多以及配准方法适合度低等问题,本文通过对SAC-IA粗配准算法的直通滤波改进,并跟传统的粗配准算法进行比较,本文的算法能够有效完成卫星点云粗配准工作;3DSC和4PCS由于卫星点云模型的特殊结构无法完成配准工作;FPFH和NDT虽然在配准效率方面较高,但是其精确性较低.首先对卫星点云的主成分分析,确定主成分方向,将点云主成分方向与Z轴重合进行坐标变换,再对其直通滤波保留卫星主体部分,接着对其进行粗配准,最后进行点云坐标变换.这样不仅保证点云有足够的特征进行配准,而且也能够有效防止配准失败和提高配准效率.

