考虑场协同的机车发动机舱散热分析及优化
王枫,荆和平,陈征,赵兴
(1.大连交通大学 机械工程学院,辽宁 大连 116028;2.大连民族大学 机电工程学院,辽宁 大连 116600;3.中国中车大连机车研究所有限公司,辽宁 大连 116021)
随着铁路运输的快速发展,对调车机车牵引力和承载能力的要求也越来越高.调车作业具有高温、高负载的特点,发动机舱热交换效率的高低将会直接影响到整车的动力性、经济性和可靠性,如果机舱内部环境温度过高,将会直接降低冷却系统的冷却性能,进而影响发动机润滑油油膜的形成,致使发动机关键部件的磨损情况加剧,发动机出现降功或停机现象,严重时会导致牵引系统产生自燃[1].因此发动机舱热管理的研究一直是重要的课题之一,优化发动机舱空间布局、提高热交换效率对于确保机舱内多个设备工作的可靠性和安全性,增加调车作业稳定性和安全性具有重要意义.
近年来,国内外学者对于机舱热管理做了大量的研究,孔繁华[2]和刘水长[3]通过安装导流板并对其进行局部优化,改善了舱内过热区的气流流量,减小了高温区域分布.唐友名[4]和Norihiko Watanabe[5]采用一三维耦合的方法,研究了发动机舱内流场特性,通过优化防撞梁设计进而改善了发动机出水温度.贾青[6]和Samer Saab[7]研究了汽车前端不同冷却部件的参数变化对进气和换热性能的影响,发现不同位置参数之间存在耦合效应.王宏朝[8]针对散热器进气不均匀问题,分析了不同矩阵型式风扇和空气流量对散热器温差场协同数和换热性能的影响,单方面改善了散热器进气不足问题.徐志明[9]基于场协同理论,研究了相同雷诺数下不同楞长的卧式半圆柱型涡流发生器的传热和流阻特性,得到最大场协同数下的楞长,进而有利于发生器的强化传热.李红智[10]针对不同型式的增压空冷器开缝翅片进行流动和传热特性分析,优化出新型开缝翅片,使其场协同性和换热性得到明显提高.
发动机舱热管理涉及机舱内部的空气流动以及高温部件之间的热量传递,目前多数研究是围绕影响发动机舱内空气流动换热影响因素,通过改进舱内结构与布局并进行单参数优化的方法来实现强化散热.国内外学者对于汽车发动机热管理做了大量的研究,但是对于铁路机车发动机舱换热研究却相对较少,因机舱热管理对于保证铁路车辆正常运行和作业具有重要意义,因此有必要对机车机舱进行热管理研究.实际上影响机舱换热因素很多,多个参数之间也存在耦合效应,单个子模块的研究和单参数的优化难以实现全局最优.近年来,考虑速度场与温度场耦合效应的场协同理论在换热器中得到了广泛的应用,但是从场协同角度出发对于解决复杂机舱内流场换热不足问题鲜有报道,考虑速度场、温度场和温度梯度场的强化散热机理的研究也相对甚少.同时对于强化散热能力评价缺乏统一的标准,因此有必要在传统评价指标基础上,基于场协同原理,以场协同角、温度效率和综合换热系数为评价指标,以提高机舱热交换率为优化目的,研究多因素控制下的整场散热优化.本文采用优化拉丁超立方试验方法提取设计参数并构建样本空间,进行二阶响应面近似模型拟合,通过非劣排序遗传算法(NSGA-II)进行全局寻优,最终得到机舱结构优化方案.
1 机舱强化散热理论基础
1.1 温度效率
温度效率,可以作为评价通风系统换热能力的评价指标[11],可表示为:
(1)
式中:f为温度效率;Te为排风口温度,K;Tz为室内平均温度,K;T0为送风温度,K.
通风系统换热能力研究过程中,排风口温度总是大于等于室内平均温度,所以温度效率总大于等于1,因此温度效率数值越大换热能力也就越好.一般情况下,实际通风换热中的温度效率在1~2之间.
1.2 场协同原理
流体与壁面之间的换热率与速度场和温度梯度场(热流场)的协同程度有着密切关系,当换热系统中的速度场和温度场达到充分协同时,换热就达到最优,流体流动所需的功耗与其换热率的投入产出比就会达到最佳[12],努塞尔数的方程如式(2)所示:

(2)
式中:Nu为努塞尔数;Re为雷诺数;Pr为普朗特数;β为换热边界空气速度矢量U与温度梯度矢量∇T的夹角,(°).
根据场协同原理,场协同角β可以作为强化散热能力评价指标,表达式如(3)所示:
(3)
式中:U为换热边界空气速度矢量;∇T为换热边界温度梯度矢量.
在速度场、温度梯度场分布一定的条件下,二者之间的夹角(场协同角)对对流传热有重要的影响,夹角越小,传热强度越高.
1.3 综合换热系数
对于机舱热管理研究,零部件表面对流换热系数的大小将很大程度上影响发动机整舱的换热效率,可以作为机舱热管理的研究指标[13],可表示为:
(4)
式中:h为综合换热系数,W/(m2·K);q为热通量,W/m2;tω为零部件表面温度,K;t0为流体温度,K.
换热系数越高,代表固体与流体之间的热交换能力越强,机舱的换热效率越高,散热效果越好.
2 发动机舱内流场分析
2.1 建立几何模型
由于机舱原始模型过于复杂,本研究在保证计算精度的情况下,对模型进行简化处理,去除模型部分零部件,保留计算需要的发动机、电机、空滤器、散热器、风扇、颗粒捕捉器等发热部件.简化的机舱模型如图1所示.

(a)机舱外部几何结构
2.2 建立网格模型
为了准确模拟机舱内流场的特性,基于风洞计算原理需要建立合理的外流场域[13],考虑到模拟中的阻塞效应,在保证计算精度的前提下,选取风洞外场计算域如图2所示.

(a) 外流域主视图
由于计算域的不规则性,全局采用非结构网格划分,对主要发热部件和机舱格栅进出口位置进行网格加密处理,为了保证模型计算精度,需对其进行网格无关性验证,网格数量124万增加到862万的过程中,观察温度效率f的变化趋势,如图3所示,当网格数接近650万左右时候,趋势逐渐趋于平缓,因此选用此网格数量进行求解计算,网格模型如图4所示.

图3 网格无关性验证

图4 对称面的外流场体网格
2.3 设置边界条件
风洞计算域采用速度进口、压力出口和无滑移壁面,机舱进出口采用内部面边界.采用多重参考系(MRF)和滑移网格方法对风扇旋转流体域进行建模,风扇转速定速2 400 r/min,采用多孔介质的方法建立散热器模型.根据文献[14]得到中冷器和散热器侧的压差关于速度的近似模型分别如式(5)、式(6)所示.
Δp1=5.172v2+13.21v
(5)
Δp2=4.353v2+3.529v
(6)
通过待定系数法求解得到多孔介质模型下的中冷器和散热器的粘性阻力系数和惯性阻力系数.
本计算工况选取低速重载条件下的运行速度10 km/h,环境温度40 ℃,风扇转速1 450 r/min,中冷器和散热器的散热功率为8.67 kW和19 kW[15].机舱内发热部件与空气之间产生强制对流换热,在不考虑辐射换热的条件下,发热部件采用热流密度边界,将文献[2]中发热部件壁面温度,通过数值仿真计算转换为热流密度,如表1所示,其他不发热部件采用绝热无滑移壁面条件.

表1 发热部件表面热流密度表 W/m2
2.4 仿真结果分析
(1)机舱内流场
机车在运行过程中,外部气流从进气格栅进入机舱后,流经电机、颗粒捕捉器、发动机和空滤器,在风扇的作用下,气流进入散热器和中冷器,带走其产生的热量,并沿着弧形风道流出机舱,舱内流线分布如图5所示.

图5 机舱内流场迹线图
从图5可以看出,由于机舱零部件的布局的非均匀性导致了舱内流线气流呈现不均匀分布,特别是发动机前侧空间过大,换热极不均匀,导致发动机油底壳位置局部温度过高(如图6所示).为了改善舱内气流分布,可以考虑通过在进气格栅位置增设导流板来优化气流路径,改善发动机内部的换热.

图6 发动机表面温度分布云图
为了有效观测机舱内部温度场和速度场的分布,所截取的观测位置如图7所示.

图7 机舱内截面选取位置
机舱内零部件分布的非均匀性不仅导致气流分布的不均匀,还影响了气流流通的通畅性.由图8所示的截面舱内速度矢量图可知,风扇上侧出现涡流,这是因为外界空气通过进气格栅进入舱内后,在风扇抽吸作用下流经发动机表面,之后遇到散热器和中冷器,导致部分气流受阻回流.
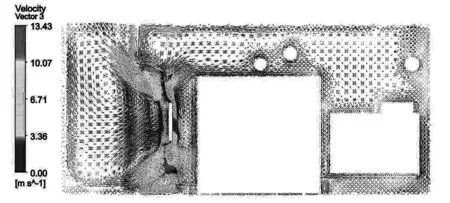
图8 Y=0截面舱内速度矢量图
通过散热器和中冷器的气流主要是由于风扇的高速旋转产生的,风扇旋转造成气流在轴向和径向运动,部分气流上升和下降到机舱顶部或底部,遇到挡板之后造成热空气回流(如图9所示),极大地削弱了换热效率.为了改善气流的分布,提高散热器和中冷器的冷却空气流量,有必要加装挡风罩,引导经过风扇之后的冷却空气尽可能多的进入散热器和中冷器,提高冷却空气利用率,挡风罩安装形式如图10所示.

图9 Y=0截面舱内温度分布云图

图10 加装挡风罩模型示意图
(2)主要零部件表面温度
气流在风扇的作用下,流经机舱零部件表面,带走其产生的绝大部分热量,零部件表面温度高低分布一方面取决于零部件散热功率,另一方面也和舱内布局有着极大的关系.
舱内主要零部件表面温度分布云图如图11所示,温度较高的位置主要集中在散热器、 中冷器、 排气歧管和颗粒捕捉器.可以看出, 散热器中心位置温度分布较高(图11(a)),这是因为风扇在旋转的过程中,风扇后侧某一区域内会形成静压区,即该位置空气流量几乎为0 kg/s,造成散热器中心区域温度过高,因此有必要合理地设计风扇与散热器的间距,减小静压区,提高散热器表面热交换效率.

(a) 散热器表面温度分布云图
颗粒捕捉器和排气歧管(图11(b))因其散热功率较大,使其表面温度分布明显较高.由于安装位置刚好处在前侧进气格栅附近,为了尽可能降低其表面温度,有必要对进气格栅进行研究,合理布置格栅开口位置,优化气流方向.
(3)场协同角
根据场协同原理可知,场协同角越小,强化散热能力越强,由图12可知,该截面位置风扇前侧散热器位置的场协同角在15°左右,整体比较小,速度场与温度梯度场的协同性较好,这是因为风扇的强制对流作用下,散热器的温度梯度平行于气流产生的速度场,换热效率较高.发动机和电机周围场协同角在75°~90°之间,整体偏高,这是因为布局太过紧密,速度与温度梯度平行性较差,换热效果降低.排气歧管位置场协同角在50°~65°之间,因为该位置零部件分布较少,气流阻力降低,场协同角分布比较均匀,波动性较小,换热效率提高.由图13可知,颗粒捕捉器周围的场协同角整体偏高,主要该位置换热效率和进气格栅处气流方向有很大的关系,只有当温度梯度平行于速度场的时候,才能增大换热效率.

图12 Y=0截面场协同角分布云图

图13 Z=1 250截面场协同角分布云图
3 机舱强化散热优化设计
3.1 试验因素和水平确定
为了有效改善机舱内的散热能力,本文以降低场协同角,提高温度效率和综合换热系数为优化目标.由于不同的结构参数之间的耦合作用会对机舱热交换效率产生不同的影响,为了得到提高机舱热交换效率的最佳参数,有必要对多参数进行优化设计.根据前面的仿真分析,本文选取进气格栅处导流板长度x1、导流板与进气格栅夹角x2、风扇与散热器间距x3和进气格栅与顶端间距x4为试验因素,如图14所示,所构建的因素水平如表2所示.
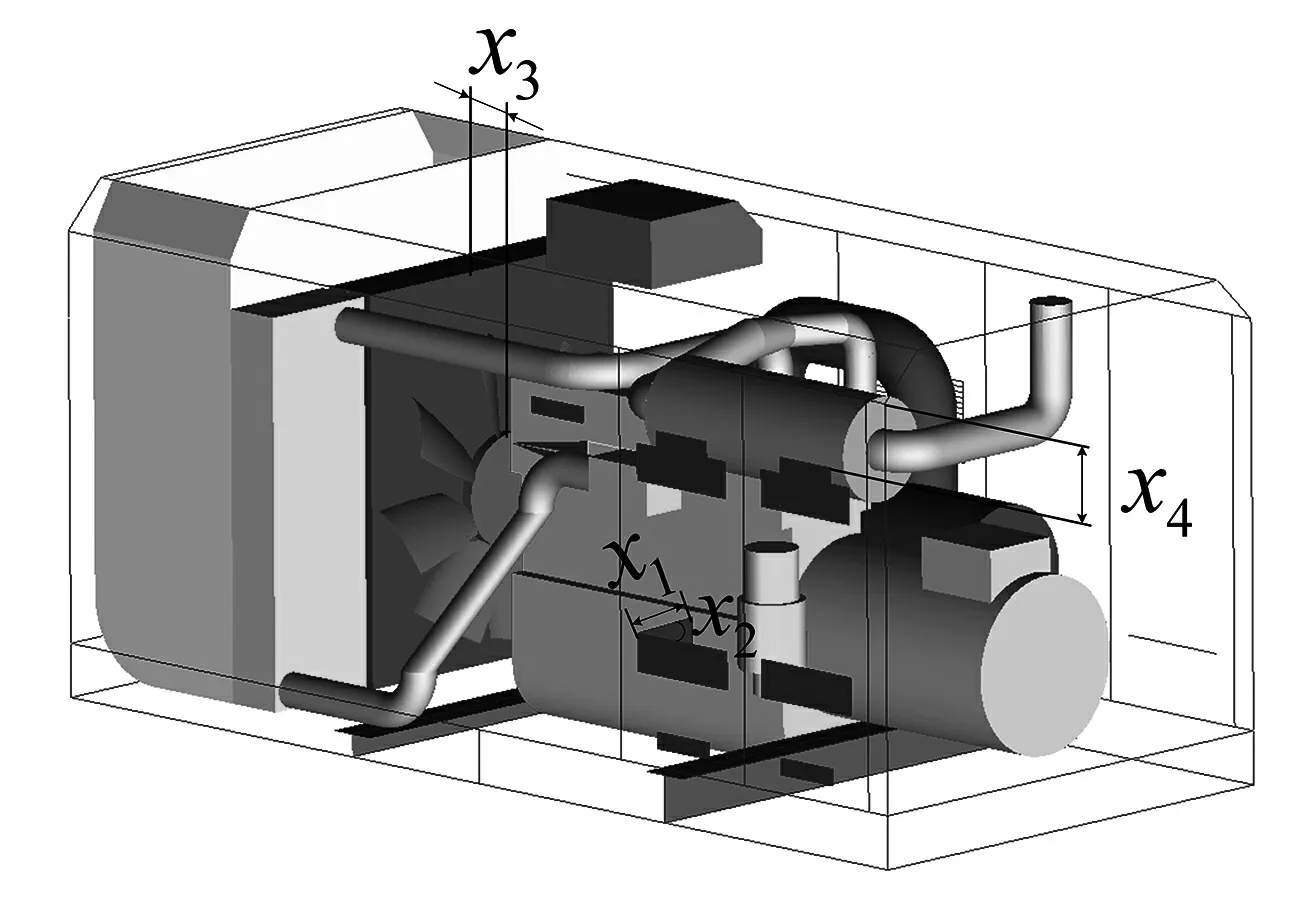
图14 试验因素示意图

表2 试验因素水平表
3.2 机舱响应面模型构建
响应面模型是采用多元回归方程来建立因子与响应之间的函数关系,对于机舱强化散热研究,机舱温度效率、综合强化换热系数和场协同角是试验因素的隐式关系函数,没有明确的表达式.因此采用二阶响应面近似模型来拟合机舱优化试验因素与响应目标之间的函数关系,其形式为:
(7)
式中:b0为近似模型常数项;bi为近似模型一次项系数;bij为近似模型平方项和交叉项系数;m为设计变量数,取值为4.
为了保证构建二阶响应近似模型的样本点在整个函数的取值空间内分散均匀,且样本数据有代表性,运用优化拉丁超立方试验设计方法进行多元参数的随机抽样,确保样本空间的均匀性[16].取部分试验设计结果如表3所示.
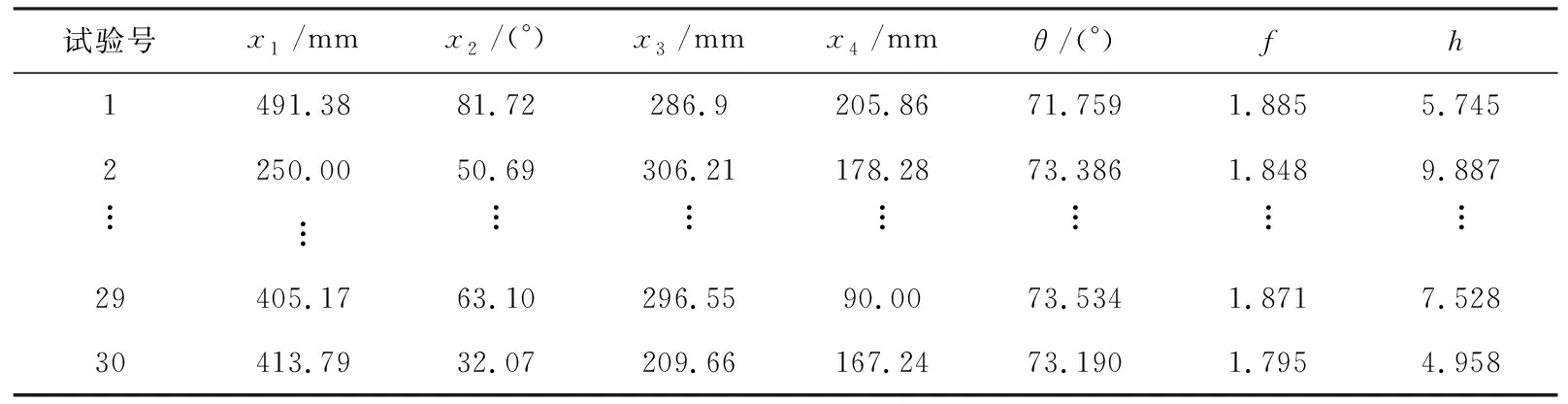
表3 优化拉丁超立方试验设计数据(部分)
根据表4可拟合出综合场协同角的二阶响应面表达式为:
(8)
温度效率的二阶响应面表达式为:
(9)
综合换热系数的二阶响应面表达式为:
(10)
为了评价响应面模型的准确性,采用修正的复相关系数R2检验方法,当R2越接近于1,表明二阶响应面模型的拟合度越好,数学表达式如式(11)所示.
(11)
其中,样本空间响应值的平均值如式(12)所示.
(12)
将设计目标响应值和预测值代入式(11),可得其修正的复相关系数.场协同角、温度效率和综合换热系数的修正的复相关系数R2均在0.9以上,表明二阶响应面模型的准确度可以满足优化设计要求.
3.3 优化设计
以参数x1、x2、x3、x4作为优化设计变量,以综合场协同角θ,温度效率f以及综合换热系数h为优化目标,则机舱热管理的优化数学模型可表示为:
(13)
多目标优化中由于优化目标间的相互制约关系,求解出来的解的集合是相互非支配的,只能根据各个目标权重大小从非劣解中选取最佳解.非劣质遗传算法(NSGA-II)是由NSGA算法改进而来,其优势是将精英策略引入到算法当中,采用快速非支配排序算法将父代种群跟子代种群进行合并,从而避免了优良种群个体在进化的过程中产生丢失,提高了优化结果的精确度.因其有着较强的自适应和鲁棒性的独特优势[17],故本文采用NSGA-II来全局寻优,求取Pareto前沿.算法中子代初始种群数设置为100,交叉概率0.93,交叉分配指数为20,变异分配指数100,迭代次数100,Pareto前沿如图15所示.

图15 NSGA-II算法Pareto最优解集
对于Pareto最优解集,考虑到将综合场协同角,温度效率以及综合换热系数同时处于一个相对最优的条件下,选取温度效率和综合强化换热系数均较优的O点作为满意解,如图15所示.优化结果如表4所示,优化后的场协同角θ由75.445°下降到了71.892°,温度效率f由1.425增大到了1.716,综合强化换热系数h也由5.924上升到8.183,目标响应得到了一定的优化改善.
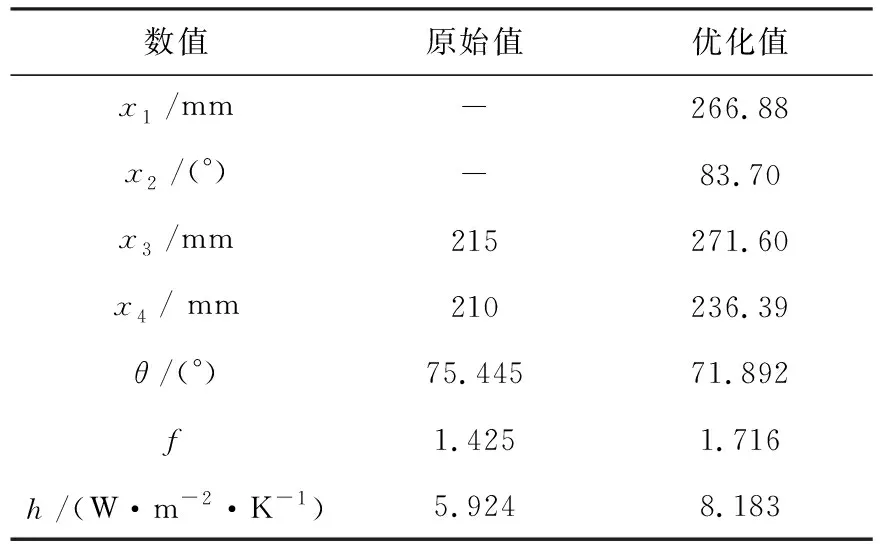
表4 优化前后设计变量和目标响应对比
优化前后Y=0截面舱内温度分布云图如图16所示.对比结果发现,增加挡风罩之后,发动机上侧高温区域明显消失,热空气回流现象得到了一定的抑制.尽管优化后排气管位置的温度还是偏高,这主要与排气管自身的散热量有关,但是发动机和电机周围的温度得到了明显下降,机舱温度分布更加合理,进而也验证了优化结果的可行性.
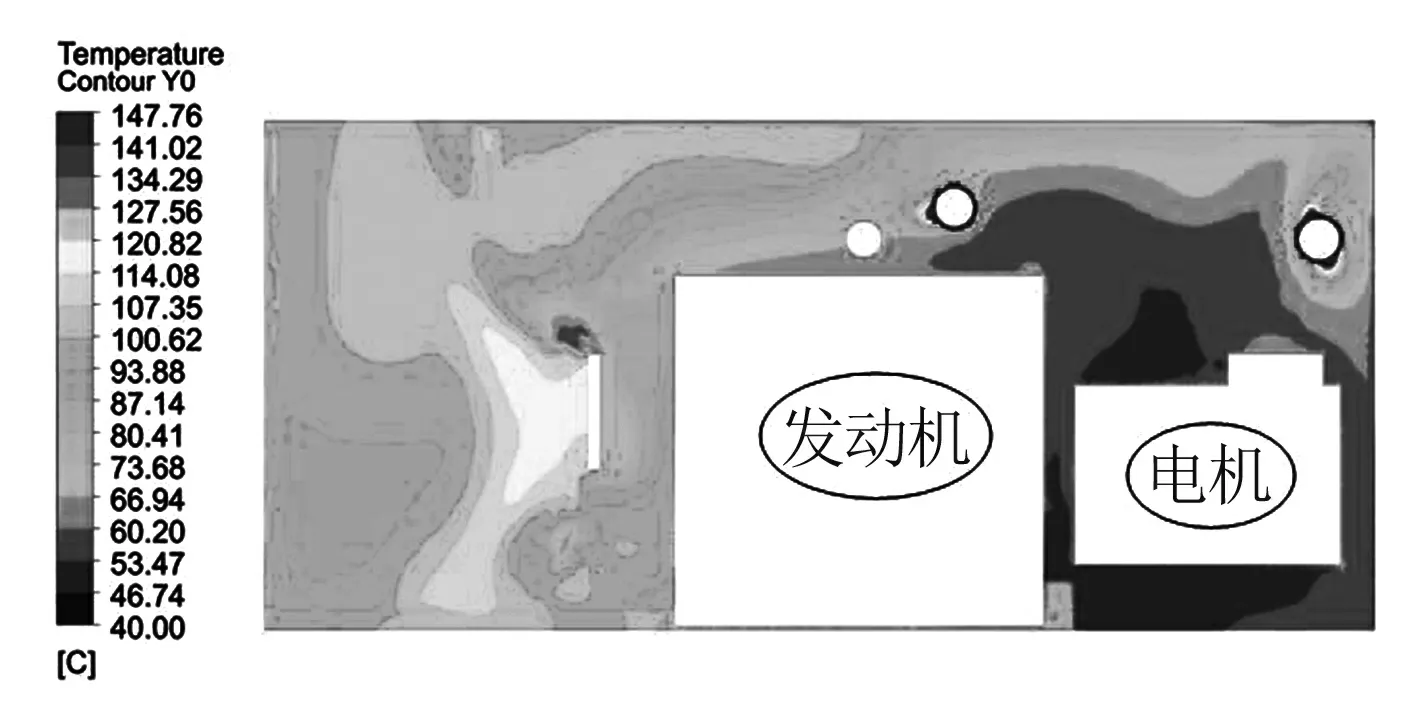
(a) 优化前Y=0截面温度分布云图
4 结论
本文以某型铁路调车机车为研究对象,引入场协同性评价指标,以提高机舱热交换效率为优化目的,采用非劣质遗传算法(NSGA-II)对构建的二阶响应面数学模型进行分析,对舱内散热器与风扇间距、导流板尺寸和角度以及进气格栅开口位置进行参数优化,优化结果发现,发动机舱温度效率和综合换热系数分别提高了18.182%、38.133%,综合场协同角降低了3.553°.研究结果表明机舱综合热交换效率得到了有效改善,为机舱热管理研究提供一定的理论参考依据.

