路内停车对通行能力及行人过街安全的影响

曹弋，王艺筱

(大连交通大学 交通运输工程学院，辽宁 大连 116028)

为减少路内停车对道路资源的占用，国内外城市多采用平行式路内停车的管理模式.研究表明，路内停车可缓解路外停车设施不足的问题且具有较好的便捷性.但也有学者认为，路内停车对城市动态交通存在显著影响.故深入研究路内停车对路段通行能力及交通安全的影响，尤为必要.

目前，国内外学者已进行了相关研究.在对交通运行状态及通行能力影响方面，Yousif S[1]等通过分析停车耗时与可接受间隙指标，研究了路内停车路段的交通运行状态.这一研究结果后来被刘晓明[2]等构建的元胞自动机模型所描述并验证.何雅琴[3]等通过分析路内停车后的剩余车道数、车道宽度及侧向净宽，定量分析了路内停车对路段通行能力与平均行程时间的影响，提出了路内停车优化策略.梅振宇[4-5]等针对车辆的离散流与连续流分别构建了路内停车影响下的机动车延误模型、跟驰模型及路内停车对机动车行驶速度的影响模型.Furth[6]等通过调查路内停车的横向占道宽度，采用统计学方法分析了有效车道宽度的分布规律.程国柱[7]等通过分析车辆饱和车头时距随路内停车数量变化的规律，构建理论模型，验证了路内停车对相邻车道的影响远大于间隔车道.在交通安全影响方面，Edquist J[8]等通过模拟驾驶实验，研究了路内停车对车辆行驶速度与驾驶员反应时间的影响.Bismark Agbelie[9]等通过研究道路几何结构和交通因素对路内停车碰撞频率的影响，得出在68.44%的道路路段中，沿着道路路段的中央分隔带的存在降低了道路停车事故的可能性.郭宏伟[10]等对本问题中非机动车越线占用机动车道的行为，采用寿命分析法进行建模，并衡量路内停车对非机动车交通安全的影响.陈峻[11]等以非机动车集群通行和压缩特性为基础，建立了路内停车影响下的非机动车压缩交通波模型.

目前大多数研究均主要侧重从有效车道宽度的折减角度，分析其对通行能力的影响.而对于车流利用可接受间隙合流行驶的情况考虑不足，且在交通安全影响方面，缺少对行人过街安全的定量研究.鉴于此，依据交通调查数据，综合有效车道宽度及可接受间隙两方面因素，探讨路内停车路段的通行能力计算方法；考虑停车视距因素，分析路内停车对行人过街安全性的定量影响关系.

1 交通调查与数据采集

1.1 调查地点

选择沈半路、登云路、上塘路及香积寺路4个路段为调查地点.上述均为城市次干路或支路，高峰时段交通并不拥挤，且均有不同负荷的非机动车交通.为了缓解路外停车设施不足的问题，上述四路段均设置了平行式路内停车设施，故而符合本研究的调查需要.调查选取的4个路段，具有不同的横断面构造特征，其几何构造如表1所示.

表1 调查路段几何构造

1.2 调查时段

研究表明，当双向双车道城市次干路中车流量大于500 veh/h时，不同路内停车比例及停车时长对动态交通影响均较为显著，路段延误率均超过20%[12].故对高峰交通繁忙时段进行调查，即早7∶00-9∶00与晚16∶00-18∶00.调查周二至周四，共计3天.

1.3 调查方法与数据采集

调查分为外业观测与内业整理两个阶段.外业观测采用视频观测法记录交通运行状态与停车状况，采用雷达测速仪抽样观测车辆速度，采用人工测量法记录各路段的占道宽度.内业整理则采用人工计数法对外业视频资料进行统计整理，可以获得断面交通量、路内停车数及交通冲突数等参数.

以第一天观测的早8∶00-9∶00时段数据为例，如表2.本次获得的交通参数，不仅将用于路内停车条件下路段通行能力模型参数的标定，还将用于路内停车对行人过街安全性影响的定量分析.

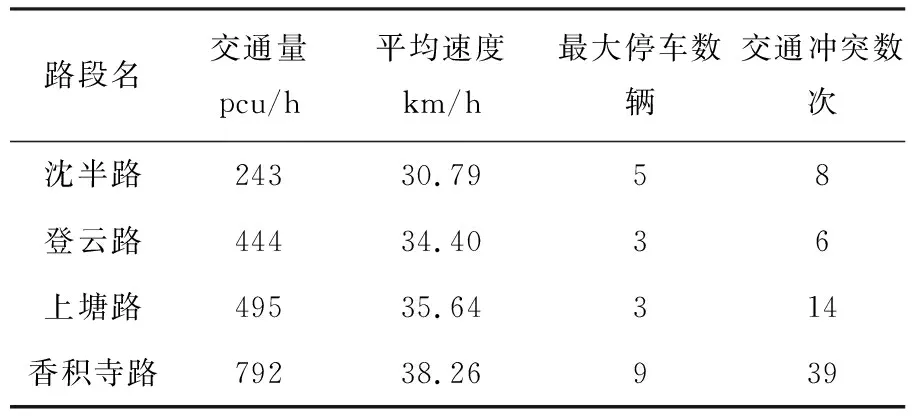
表2 第一调查日的交通数据(8∶00-9∶00)

2 路内停车对路段通行能力的影响

路内停车路段的通行能力，以停车所在车道及其内侧相邻车道所受影响最为显著，故而通行能力的分析与计算应围绕上述车道进行.

经验表明，路内停车将占用道路的横向空间.而道路剩余横向宽度的大小，将直接影响动态交通的通行状况.故而，路内停车对路段通行能力的影响，也应根据道路剩余横向宽度的大小，分以下两种情况进行讨论.

2.1 车道有效宽度的折减

将路内停车相邻车道的内侧车道线至路内停车区内边缘的距离，定义为横向剩余宽度，记为WS.交通观测表明，当WS大于某一值时，路内停车路段的剩余横向空间可供两条车道并行调剂使用，如图1所示.

图1 横向剩余宽度及车道调剂

依据文献[13]的研究方法，考虑车辆行驶的侧向安全距离与车辆标准宽度，按低速行驶，计算确定横向剩余宽度WS的临界值如表3所示.

表3 横向剩余宽度WS的临界值

当横向剩余宽度WS大于表3中临界值时，车道通行能力由于车道有效宽度的减小而降低.可用HCM[14]中关于车道宽度的修正方法，对该情况下的车道通行能力进行折减，如式(1)与(2)所示.

Cl1=Cl2=C0·fw

(1)

(2)

式中：Cl1与Cl2分别为图1中车道1与车道2的通行能力，pcu·h-1；C0为一条车道的基本通行能力，pcu·h-1，应据设计速度查表获得；fw为车道宽度修正系数；Wc为一条车道的标准宽度，m；参数9.144为英制单位换算为公制单位所得常数.进一步分析表明，此时，由于其车辆通行的侧向余宽不足且外侧车道线失去交通意义，将对交通安全产生极为不利的影响.

2.2 可接受间隙模型

当路内停车后，道路横向剩余宽度不满足表3中所列临界值时，主线车流无法并排通过.此时，外侧车道1中的车辆将被迫利用其相邻车道车队的可接受间隙实现合流行驶，如图2所示.此时路内停车段将产生严重的通行能力瓶颈，这种合流运行将导致大量交通冲突的产生，进而影响原有车道2的通行能力.

现假设车道2内车流的车头时距h，服从参数为λ的负指数分布.则h的分布函数如式(3)所示.

F(t)=P(h≤t)=1-e-λt

(3)

设t0为车道2内车流的临界时间间隔，即车辆驶入该车流所需的最小车头时距.t表示车道1内的车流能够连续驶入车道2的跟驰车头时距.车道1内，共有n辆车等待驶入车道2.那么，允许n辆车驶入的车道2内车流的车头时距概率可由式(4)计算.

(4)

由于车道1中有n辆车等待，因此当车道2内的车流出现大于t0+nt的车头时距时，车道1中仍然有n辆车驶入车道2.因此，出现上述情况的概率可用P′(n)表示，其计算公式如式(5)所示.

(5)

设ql2为车道2上游路段的交通量，pcu·h-1.则ql2同时也表示车道2内车队的车头时距总数.因此，车道1中能够驶入车道2的车辆数Q(pcu)可由式(6)计算

(6)

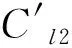
(7)

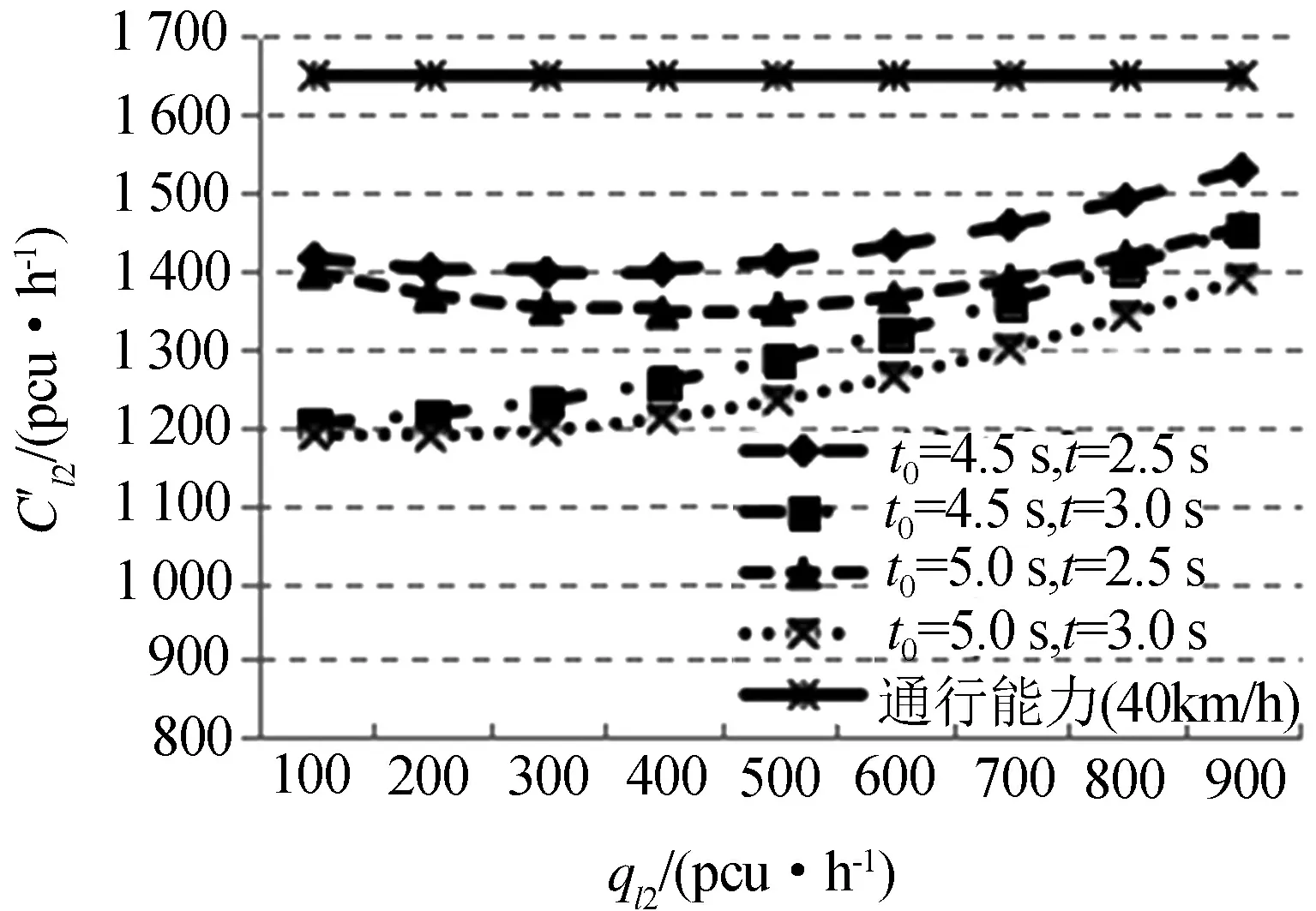
图3 不同条件下的车道2通行能力

从图3可以看出，不同t0和t对应的车道2通行能力曲线，都随着该车道内交通量的增大而先减小后增大，且所有通行能力值均小于该条车道的基本通行能力.进一步分析表明，该情况下车道2的通行能力除受车道2的可接受间隙与车道1的跟驰车头时距影响外，更主要由车道2的车流量确定，且该流量的决定作用是双向交互的.即当该流量较小时，车道1中的车辆利用可接受间隙进行合流的车辆数较多，对通行能力有一定补偿；相反，当该流量较大时，车道1中将仅有少数车辆能够合流通过该路内停车段.

定义一个负影响指标α来描述路内停车对道路通行能力的负面影响，如式(8)所示.

(8)

式中：Cl为车道实际通行能力，pcu·h-1；C0为无路内停车情况下，某设计速度的普通车道基本通行能力，pcu·h-1.

3 路内停车对行人过街安全的影响

本文主要研究对象为次干路及以下等级道路，行人过街为无人行横道和信号灯的情况下过街，对有人行横道但行人不遵守交通规则时，也同样适用.路内停车对行人过街安全的影响，主要来源于停车对机动车驾驶员视线的遮挡，故而借鉴文献[15]的分析思路，从停车视距的角度进行分析，如图4所示.

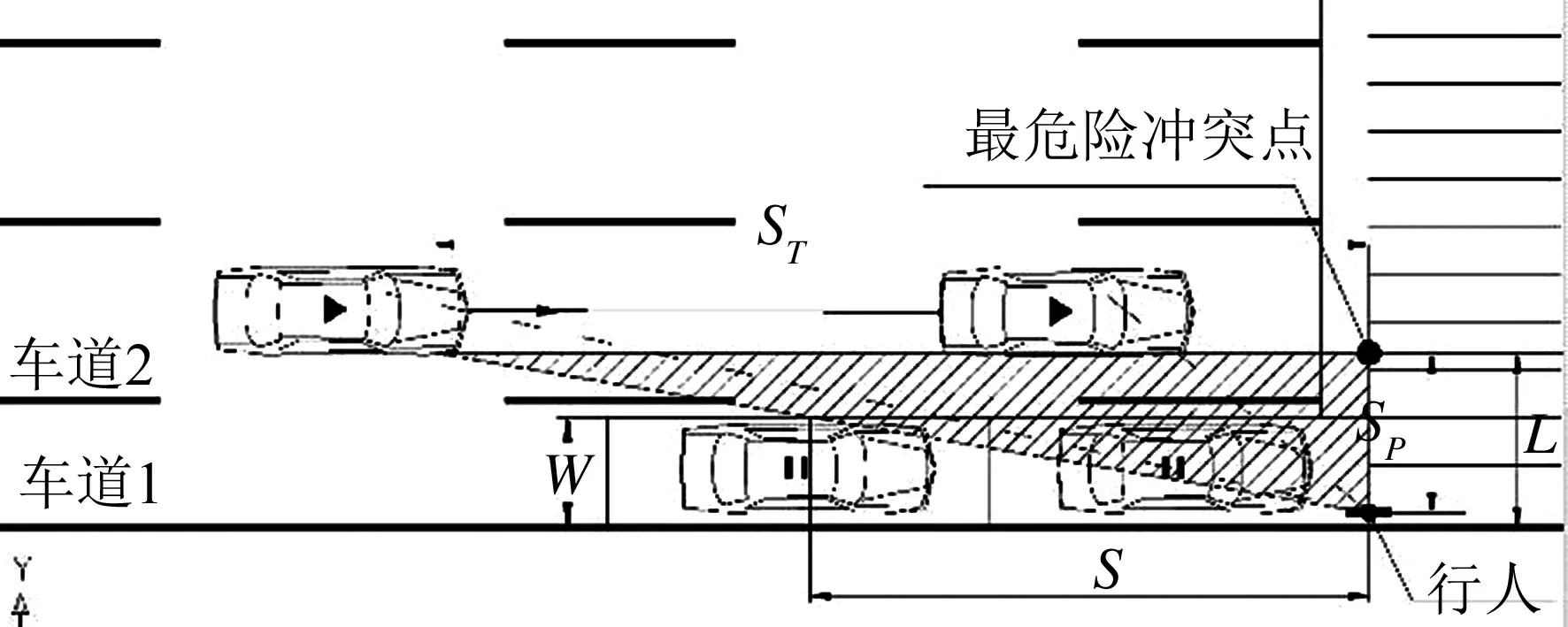
图4 路内停车对过街行人安全性的影响

根据上述影响机理，首先确定过街行人与机动车的最危险冲突点位置.而后自该冲突点分别沿机动车行驶方向及行人行进方向截取停车视距ST与行人视距SP，构成视距三角形.本文基于最不利原则考虑，即路内停车时视距三角形内如有停车，不论车辆类型均视为驾驶员及行人视线被全部遮挡.为使路内停车不至遮挡驾驶员视线，故而要求在视距三角形范围内，不应有路内停车的存在.上述分析有助于在行人过街路段，安全合理的布置路内停车区间.由于大货车在行进时相较于其他车型具有视点高等视距优势，且城区中少有设置大货车路内停车点，故在此不做考虑.

机动车停车视距ST，可由式(9)计算得到.假定行人以一恒定速度过街，则其临界距离SP可由式(10)计算.至此，路内停车区终点至过街人行横道边缘的安全距离S，可由视距三角形的几何关系得到，如式(11)所示.

(9)

(10)

(11)

式中：VT表示路段上车辆的平均行驶速度，km·h-1；tr表示驾驶员反应时间与车辆机械生效时间之和，s；出于安全考虑，通常取2.5 s；φT为车辆轮胎与路面的摩擦系数，基于最不利设计原则，即考虑冰雪路面情况，该值应取路面湿滑条件下的摩擦系数，即0.3；f为车辆轮胎的滚动阻力系数，通常取0.02；i为道路纵坡，按车辆行进方向，上坡为正；VP为行人过街的行进速度，按不利情况考虑，可取5 km/ h；W为路内停车区的宽度，m；L为最危险冲突点至道路边缘的垂直距离，m.

4 实例分析

4.1 通行能力分析

(1)计算方法的选择

根据表1中的调查路段几何构造数据，计算路内停车后路段横向剩余宽度WS，并与表3中的数据进行对比，可选定路段通行能力的计算方法.路段横向剩余宽度计算结果如表4所示.

表4 剩余宽度WS计算结果

由表4的计算结果可知，调查的4个路段的车道横向剩余宽度WS均小于其临界宽度，说明外侧车道的车辆只能寻求其内侧相邻车道中车队的可接受间隙通过.故而均应采用可接受间隙公式计算通行能力.此外，注意到登云路的横向剩余车道宽度为2.7 m，小于一条车道的标准宽度，因此计算其通行能力时，还需要进行车道宽度折减计算.

(2)计算结果与分析

以第一天调查的早7∶00-9∶00与晚16∶00- 18∶00的4路段路内停车区内侧相邻车道的交通量数据为基本参数，采用式(7)计算各路段路内停车区内侧相邻车道的通行能力.计算时，该车道车队的临界间隔时间t0取4.5 s，连续穿越车队的跟驰车头时距t取2.5 s.计算得到的四路段路内停车区内侧相邻车道的通行能力及各小时车道交通量如图5所示.

图5 停车区内侧相邻车道的交通量及通行能力

由图5可知，各车道的通行能力变化较小.其中沈半路、上塘路与香积寺路的路内停车内侧相邻车道通行能力均为1 400 pcu/h左右；而登云路该 车 道 由 于 受 车 道 宽 度 折 减 的 影 响， 通 行能力为1 240 pcu/h左右.与无路内停车情况下30 km·h-1设计速度的普通车道通行能力相比，该计算结果低于基本通行能力1 600 pcu/h，且由式(8)得，此时沈半路、上塘路与香积寺路的负影响指标为12.5%，登云路的负影响指标为22.5%.

由上述分析可知，该车道的通行能力受车道本身交通量的影响很小，而受路内停车的影响较为显著.

4.2 行人过街安全分析

由表4可以看出，路内停车区终端至人行横道上游边界的安全设置距离很大程度上由车辆的平均行驶速度决定.登云路的早高峰实测平均车速为34.4 km/h，而其路段限速为40 km/h.调查路段中，仅登云路有人行横道.通过现场实测得到W为2.5 m，L为4 m，路面水平.

不同平均行驶速度所对应的安全距离S，即从人行横道上游边界至路内停车区终点的距离，可由式(9)～式(11)计算并列于表5中.

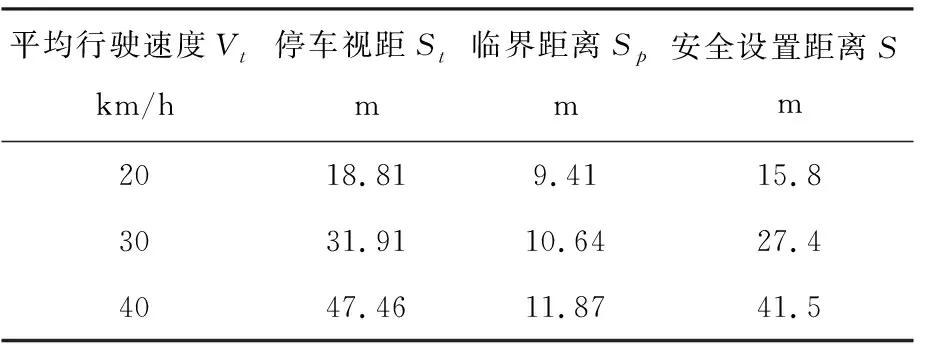
表5 由停车区至人行横道的安全设置距离

本着偏安全设计理念，路内停车区设置应考虑最不利因素，即冰雪路面等极端条件，故由表5得，在设计最高平均行驶速度40 km/h条件下，其路内停车区应位于人行道上游方向41.5 m以外开始设置.进一步比较分析表明，上述数值均远大于现行欧洲标准所限定的5 m.欧洲标准的制定，是基于一般情况的考虑，而不是最不利情况.即在冰雪路面或路面湿滑等特殊条件下，5 m的安全设置距离无法保证安全视距.所以，上述路内停车区的设置标准，比现行的欧洲标准更为具体、安全.

5 结论

(1) 路内停车对路段通行能力具有显著影响.应根据停车占道后的横向剩余宽度，选择车道有效宽度折减或可接受间隙理论进行通行能力计算.当主线交通的平均速度介于30～40 km/h，且仅有车辆合流行驶时，路内停车影响下的通行能力较一条车道的基本通行能力减少12.5%；当合流行驶与车道宽度折减同时存在时，将减少22.5%；

(2) 路内停车对行人过街安全性的影响，取决于机动车驾驶员的停车视距是否得以满足.自人行横道至停车区的安全设置距离，很大程度上取决于主线交通的平均行驶速度.而本研究计算得到的安全距离值，大于现行多数设计标准的推荐值.

本研究选择了4个路内停车路段开展交通调查，尽管调查地点数量偏少，但理论分析与案例分析结果的一般性规律仍可为同类研究所借鉴.调查地点偏少的问题，可在后续研究中不断补充加强.