基于微环谐振腔的宽带纠缠源制备方案

唐晓帆

(上海交通大学电子工程系,上海 200240)

0 引言

量子通信[1]是结合量子力学和经典信息学科而产生的一门交叉学科。由于量子特有的纠缠特性[2],在信息传输的有效性、可靠性、安全性等方面,量子通信具有经典通信无法超越的优势。量子纠缠源作为量子通信系统的信号源,在基于量子纠缠的量子通信系统中扮演着不可或缺的角色,近年来引起广大研究者的兴趣。特别是能够产生多组份量子纠缠态[3]的纠缠源,由于本身具有的多纠缠态,在实现复杂的量子信息处理算法[4]以及量子加密协议[5]等应用中具有极大的潜力。

本文利用氮化硅微环谐振腔[6]制备出的宽带纠缠源可以产生八对双组份连续变量量子纠缠态。分别对每对量子纠缠态进行仿真验证,发现全部存在纠缠关系。受微环谐振腔结构色散的影响,仅对前八对双组份纠缠态进行了研究。从微环谐振腔的物理模型出发对腔内的光场进行分析,研究了腔内各种模式的演化,并结合相关实验参数分别仿真得出了八对双组份量子纠缠。本文的仿真参数可为实验实现提供理论参考。

1 三阶非线性微环谐振腔演化

1.1 物理模型

如图1所示,所设计微环谐振腔[7]的物理模型由三部分组成。第一部分是耦合信道,位于图1的最下方,泵浦光从激光器注入到耦合信道中。第二部分是微环,它与耦合信道构成一个激光分束器[8],耦合信道中的泵浦光以一定的效率被耦合进微环中。被耦合进微环的泵浦光会在微腔内做绕环运动,每一圈都有一部分光被耦合回耦合信道,从输出端口输出。微环是由三阶非线性材料制成[9],泵浦光在环内行进时会发生三阶非线性效应,产生信号光和闲置光。第三部分是损耗信道,位于图1的最上端,该信道实际并不存在,是为了模拟环境对量子信号的影响,将原子吸收、散射[10]等原因造成的光子损耗看作被耦合进了损耗信道。

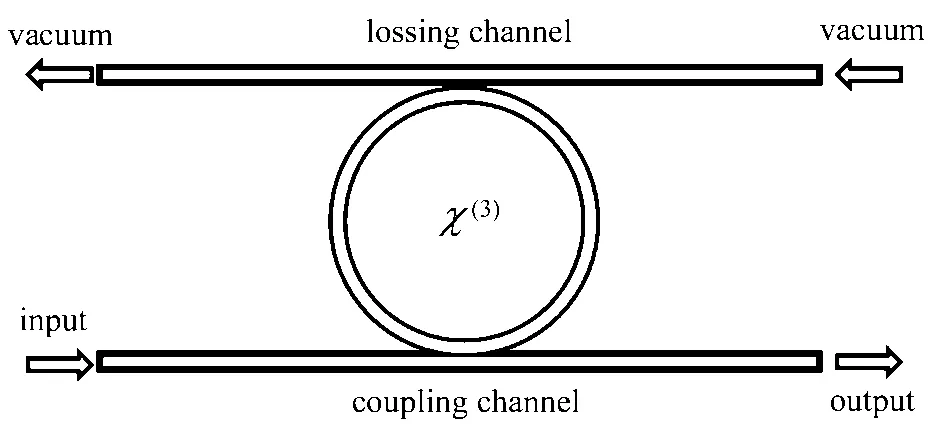
图1 微环谐振腔结构Fig.1 Structure of the microring resonator

1.2 光场分析

当打入频率为Ωp的泵浦光后,一部分泵浦光被耦合进微环,在三阶非线性的作用下微环内会发生自发四波混频效应(SFWM)[11,12],产生频率为Ωs的信号光和频率为Ωi的闲置光。根据能量守恒定律有

光腔的谐振频率用ωj表示,j=p,s,i。如图2所示,由于材料的色散导致了ωj和Ωj有偏差,为了量化色散,定义了每一种模式的失谐量Δj=ωj-Ωj,并用D3=2Δp-Δs-Δi=2ωp-ωs-ωi表示整个系统的失谐量。

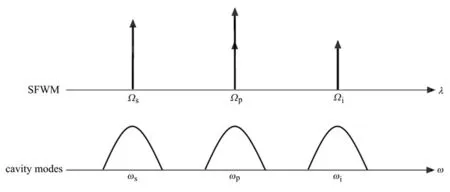
图2 四波混频和光腔的谐振频率Fig.2 SFWM and the resonant modes

所设计谐振腔的谐振峰位置满足

式中:d1=6.1562×1012rad/s,d2=1.3604×108rad/s,µ代表了不同的参量过程。泵浦光频率位于微环谐振峰的位置,将此谐振峰编号为0,即ω0=ωp=Ωp。由于信号光和闲置光对称分布于泵浦光的两侧,所以信号光和闲置光的谐振频率可以表示为:ωs=ω-µ,ωi=ωµ。通过以上公式,可以得出所有参量过程的系统失谐量为D3=-d2µ2。

1.3 演化分析方法

对于系统的演化分析,参考了文献[13-17]提出的方法。从系统的哈密顿量出发,运用海森伯格方程,并结合谐振腔的输入输出关系得到了海森伯格-朗之万方程。接下来再对海森伯格-朗之万方程进行旋波近似操作,将经过旋波近似操作后的方程进行线性化,得到了稳态方程和量子涨落方程。最终求解得到了判断信号光和闲置光之间是否存在纠缠关系的判据,以及与纠缠判据相关的参数之间的函数关系。

2 仿真结果与讨论

2.1 仿真参数

仿真中用到的参数具体数值为:腔的品质因子Q=106,连续泵浦光的波长1.55×10-6m,群速度vg约为光速,三阶非线性系数γ=1(Wm)-1。信号光和闲置光的纠缠度用E表示,输入泵浦光的归一化功率为其中ħ是约化普朗克常数,Γ=2×108Hz是微腔谐振峰的线宽,η=0.55Γ是耦合抑制率,Pin是实际输入的泵浦光的功率。

这里研究了八对双组份的量子态,其参量过程分别用µ=1,2,3,4,5,6,7,8表示。不同参量过程所对应的失谐量D3如表1所示。

表1 不同µ对应的D3值Table 1 The values of D3for differentµ

2.2 数值仿真结果

运用上述仿真参数,可以得到每一组量子态的纠缠度。对于纠缠度的测量,根据Duan等[18]提出的纠缠判据,这里把纠缠度定义为其中Δ-和Δ+是两个算符,具体的计算过程可以参考相关的文献。图3给出了每一组份量子态的纠缠度与归一化输入泵浦光功率之间的关系。横坐标是归一化输入泵浦光的功率,纵坐标为信号光和闲置光的纠缠度。纠缠度小于零表示信号光和闲置光存在纠缠关系,且纠缠度的值越小越好。可见,当使用设计好的微腔时,只要控制好输入泵浦光的功率,就可以制备出八对双组份量子纠缠态。

图3给出了八个参量过程的仿真结果,从图中可以看出八组量子态的纠缠度都是小于0的,所以说该八对双组份量子态都是纠缠态。

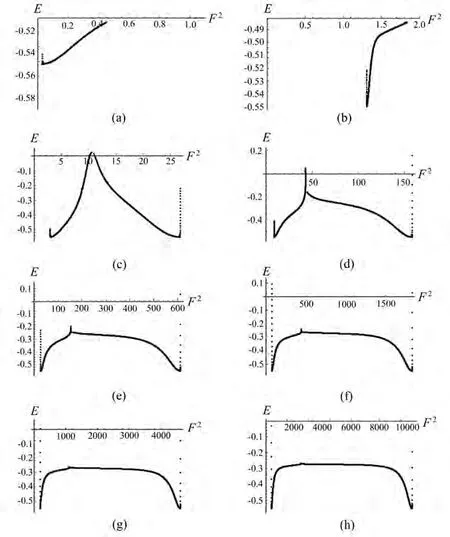
图3 八对双组份量子态纠缠度的仿真结果。(a)D3=-0.6802;(b)D3=-2.7208;(c)D3=-6.1218;(d)D3=-10.8832;(e)D3=-17.005;(f)D3=-24.4832;(g)D3=-33.3298;(h)D3=-43.5328Fig.3 Simulation results for the degree of entanglement for eight pairs of photons.(a)D3=-0.6802;(b)D3=-2.7208;(c)D3=-6.1218;(d)D3=-10.8832;(e)D3=-17.005;(f)D3=-24.4832;(g)D3=-33.3298;(h)D3=-43.5328

3 结论

通过上述仿真结果可以看出,所设计出的氮化硅微环谐振腔可以实现八对双组份量子纠缠态,满足预定宽带纠缠源的设计要求。并且根据仿真结果图可以看出,通过调整输入泵浦光的功率可以有效地提高纠缠度。此宽带纠缠源可以直接应用到一些量子通信系统中,比如在一个全连接的量子安全通信网络中,四方可以同时进行量子通信。后续还可通过优化腔的结构和参数来制备出更多对的量子纠缠态。