可见光/红外双波段离轴四反光学系统设计

曹一青,沈志娟

(1莆田学院机电与信息工程学院,福建 莆田 351100;2福建省激光精密加工工程技术研究中心,福建 莆田 351100)

0 引言

随着现代科学技术的发展,空间光学领域对目标进行探测和识别的要求越来越高,空间光学仪器逐步向高分辨率、小型化和轻量化等方向发展,给此类科学仪器中光学系统设计带来挑战[1,2]。目前光学系统可以分为折射式、反射式和折反射式系统。相比于折射式和折反射式光学系统,反射式光学系统具有无色差及二级光谱问题、光路可折转、体积小和对温度和气压变化不敏感等优点,使得它在像质优良、轻量化、实现大口径和多波段设计中具有明显优势,因此此类系统被广泛应用于空间遥感技术、航天侦察和天文观测等领域[3]。反射式光学系统结构又可分为同轴和离轴两类,同轴反射式结构由于视场角较小,次镜对主镜中心存在遮拦导致光能利用效率降低,导致成像质量下降等问题,使其应用具有一定局限性;而离轴反射式结构能避免同轴结构带来的上述问题,使得目前该种结构的反射光学系统得到了广泛应用,研究人员对该类系统的设计方法进行了不断探索[4,5]。

根据光学系统中含有的反射镜数量,它能分成离轴三反、四反和五反等。由于离轴五反光学系统镜片数量多、成本高且安装调整难度大,其在实际中很少应用,目前研究基本上聚焦于离轴三反、四反系统。Cao等[6]应用节点像差理论及遗传算法得到较合适离轴三反系统初始结构;Zhu等[7]提出了一种离轴三反光学系统初始结构解析解求解方法,设计了一种具有矩形视场小F数的自由曲面离轴三反光学系统;Liu等[8]以离轴三反光学系统为研究对象,推导了系统线性像散平衡条件,采用倾斜母镜光轴的方法设计了一种大相对孔径、大视场像散校正的斜轴离轴三反光学系统;Huang等[9]基于矩阵光学理论构建非线性方程组,对其求解从而得到满足要求同轴四反光学系统初始结构,然后不断调整系统各反射镜偏心和倾斜,并结合自由曲面来对它进行优化设计。

离轴四反光学系统相比于三反系统具有更多设计自由度,像差平衡和校正能力强,同时随着加工工艺和装调技术不断发展,使得此类系统应用成为未来发展趋势,其设计方面的相关问题是目前研究得难点和热点,因此本文提出了一种离轴四反光学系统设计方法。首先,基于同轴四反光学系统像差分析表达式推导了系统均方根波像差计算公式,并以此构建系统成像质量评价目标函数,利用自适应变异概率遗传算法对其进行求解,得到较合适系统初始结构参数,再对系统进行离轴处理,并引入非球面校正系统非对称像差。基于上述方法设计了一种离轴四反光学系统,证明本文所讨论设计思路在此类离轴反射光学系统中具有一定的实际应用潜力。

1 同轴四反射镜光学系统设计思路

在同轴结构情况下,使系统中反射镜偏心及倾斜就能得到离轴反射镜系统,达到消除同轴光学系统带来的中心遮拦问题,并能有效校正和平衡系统像差。图1为同轴四反光学系统结构及光路图[10,11],该系统由主反射镜M1、次反射镜M2、第三反射镜M3和第四反射镜M4组成,光线依次经过反射镜M1、M2、M3和M4反射后到达像平面I上,并分别与其相交于O1、O2、O3、O4和O;di(i=1,2,3)为沿中心轴反射镜Mi与Mi+1之间距离,d4为沿中心轴反射镜M4与像平面之间的距离;li和分别为反射镜Mi的物距和像距,hi为第一近轴光线在反射镜Mi上的投射高度;另外,将反射镜Mi定义为非球面且对应的二次非球面系数为

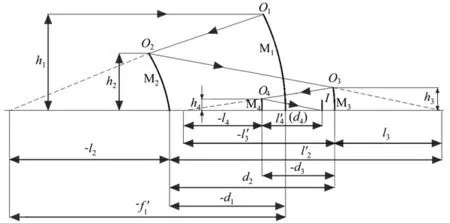
图1 同轴四反光学系统结构及光路图Fig.1 Structure and optical scheme of a coaxial four-mirror reflective optical system

根据光学几何关系,反射镜Mi+1对M1的遮拦比αi和反射镜Mi的放大率βi的计算表达式分别为

对于焦距为f′的无限远同轴四反光学系统,光阑设定在反射镜M1位置处,对其近轴光线进行光线追迹,结合(1)式给出的遮拦比和放大率关系式,推导出反射镜Mi的曲率半径ri,以及两反射镜Mi与Mi+1之间距离di的计算表达式为

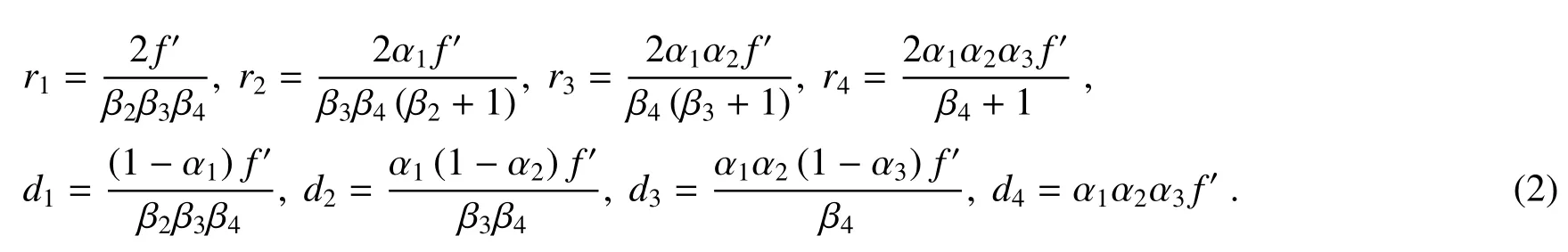
然后,基于赛德尔像差理论中的初级像差系数表达式,结合(1)、(2)式,得到关于遮拦比、放大率和二次非球面系数的同轴四反光学系统总的球差S1、彗差S2、像散S3和场曲S4的像差系数表达式,可分别表示为[12]

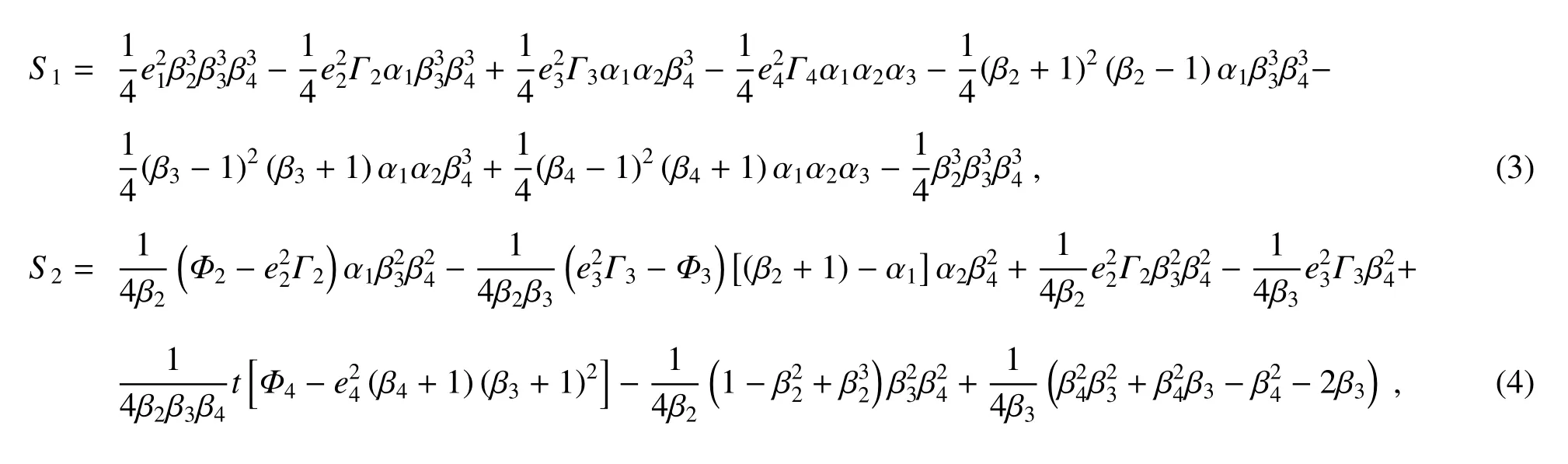
对于同轴反射镜光学系统,仅考虑初级像差时,该系统波像差计算表达式为[13]

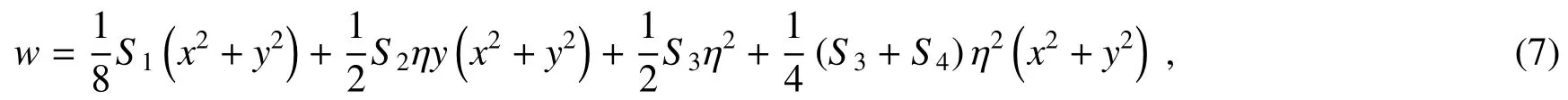
式中:x,y为归一化的光阑坐标;η为归一化的物面坐标。然后,在(7)式的基础上,通过积分方法可以得到系统均方根波像差表达式为

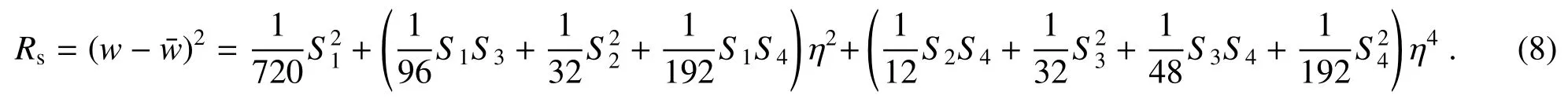
合适的初始结构在光学系统设计中起到至关重要的作用,因此根据上述像差系数表达式,利用消除初级像差的条件建立方程组,对其求解得到系统初始结构参数。由于像差系数表达式非常复杂,很难直接得到解析解,提出构建系统目标函数作为最终设计目标,具体表达式为

式中:ωi(i=1,2,···,k)为函数Pi对应的权重系数,其取值可以根据实际设计需要进行调整;Pi表示在归一化物方坐标ηi情况下应用(8)式计算得到的系统均方根波像差。

表达式给出的目标函数Φ是对光学系统成像质量的综合评判,其数值越小表示系统像差越小,成像质量越高。由于该目标函数是关于系统光学参量的函数表达式,直接对该目标函数进行解析求解非常复杂,开发了一种自适应变异概率的遗传算法对其进行优化得到最优解,最终得到同轴四反光学系统的初始结构参数。

结合自适应变异概率的遗传算法是一种高度并行、随机和自适应变异的全局优化算法,具有鲁棒性好和计算效率高等特点,适用于高维度非线性的优化问题。应用这种遗传算法优化(9)式所表示的目标函数,具体过程主要包括编码和初始种群确定、计算适应度值、交叉、自适应变异、判断是否达到足够迭代次数、解码并输出初始结构参数,整个过程的设计流程图如图2所示。

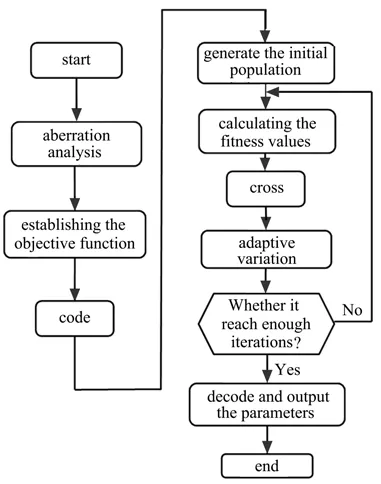
图2 应用自适应变异概率遗传算法求解同轴四反光学系统初始结构参数流程图Fig.2 Flow chart of solving initial structure parameters of four-reflective mirrors coaxial optical system using adaptive variation probability genetic algorithm

通过Matlab软件平台编写自适应变异概率遗传算法程序,计算出同轴四反光学系统各块反射镜的半径和间距,得到此类系统初始结构,经过离轴处理和进一步像差优化就能得到离轴四反光学系统。

2 离轴四反光学系统设计实例与性能分析

2.1 离轴四反光学系统设计

根据设计离轴四反光学系统的技术指标,应用上一节讨论方法得到一种合适同轴四反射镜光学系统的初始结构参数,然后对系统各块反射镜进行偏心及倾斜处理,并对其进行像差校正。离轴四反光学系统主要技术指标如表1所示,此类系统设计步骤如图3所示。

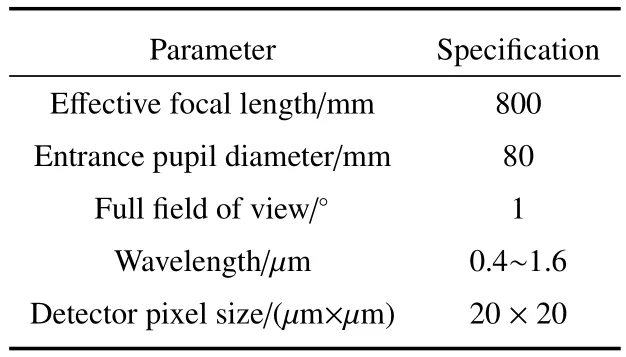
表1 离轴四反光学系统技术指标Table 1 Specification of off-axis four-mirror reflective optical system

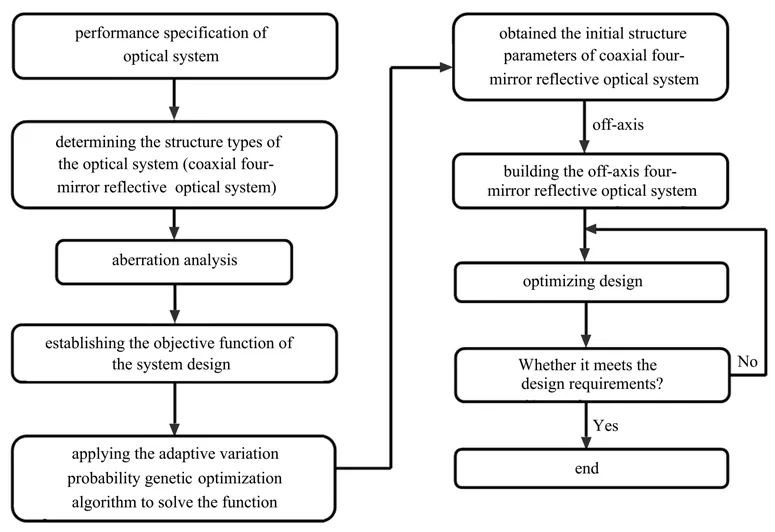
图3 离轴四反光学系统设计步骤Fig.3 Design steps of off-axis four-mirror reflective optical system

根据离轴四反光学系统的设计步骤,首先需要求解出同轴四反光学系统合适的初始结构参数,应用改进后的遗传算法对构建此类光学系统成像质量的目标函数进行优化,在优化计算之前必须要确定目标函数中所有变量的变化范围。对推导出的同轴四反光学系统像差系数表达式(3)～(6),系统初级球差S1表达式与所有反射镜二次非球面系数有关;同时,由于轴外点像差与主反射镜M1二次非球面系数e21无关,因此该反射镜一般采用抛物面镜,即e21取-1,仅通过选择改变反射镜M2、M3和M4的二次非球面系数来校正初级球差;初级彗差S2使用反射镜M2、M3和M4的二次非球面系数来控制;初级像散S3通过改变反射镜M2和M3的二次非球面系数来校正;初级场曲S4仅与系统结构有关,与各反射镜的二次非球面系数无关。在该设计中,目标函数中各个变量取值范围可由表2给出。

表2 目标函数各个变量取值范围Table 2 Range of values for each variable of the target function

应用MATLAB软件平台对自适应变异概率遗传算法进行编程,在上述构建的系统成像质量目标函数和各个变量取值范围基础上求解同轴四反光学系统初始结构光学参数。首先,在(9)式中设置η1=0、η2=0.707、η3=1,以及其对应的权重系数分别定义为w1=w2=w3=1;然后,采用自适应变异概率的遗传算法对该系统目标函数进行优化,在优化过程中该算法相关主要参数设定为种群数量为100,交叉概率为0.8,最大进化代数为2000代。应用上述目标函数优化过程,对其进行优化20次,分析运行结果得到该目标函数的最优解为 α1=0.383,α2=0.479,α3=0.789,β2=-2.125,β3=-1.376,β4=-1.026,e2=-0.548,e3=4.264和e4=4.470;最后,结合主反射镜M1为抛物面镜,并应用(2)式就能计算出同轴四反光学系统初始结构参数,具体如表3所示。

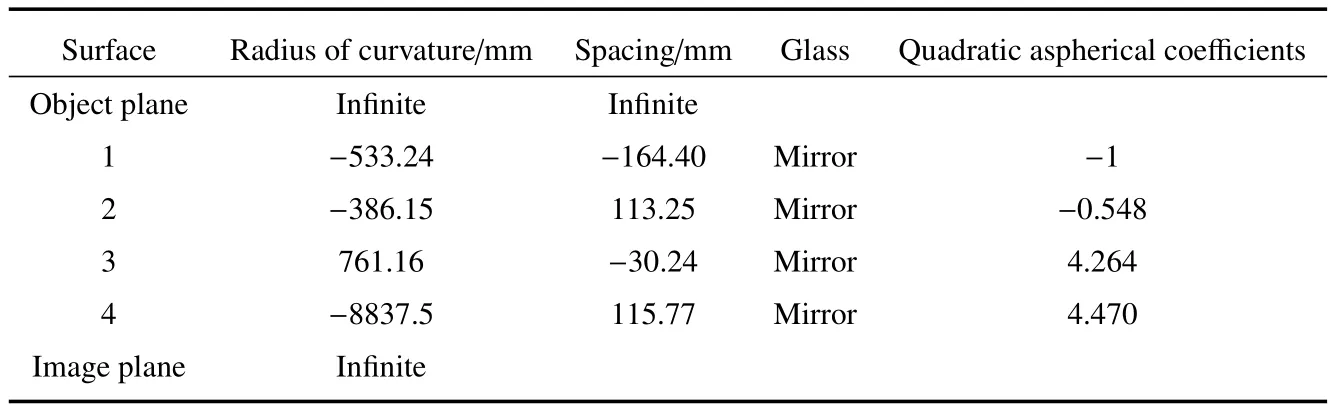
表3 同轴四反光学系统初始结构参数Table 3 Initial structural parameters of coaxial four-mirror reflective optical system

同轴四反光学系统初始结构确定后,为了增大光学系统视场及避免中心遮拦,对其进行离轴处理得到离轴四反射镜光学系统,同样将孔径光阑放置在反射镜M1处,再应用光学设计软件Zemax对系统进行反复像差优化。

首先,离轴四反射镜光学系统在大孔径成像情况下高阶像差影响较大,同时离轴系统的轴外像差一般较大,因此在优化设计过程中将系统中各块反射镜设计为偶次非球面来校正这些像差,其对应的面型表达式为

式中:z和k分别表示非球面的弧矢高度和二次圆锥系数;c=1/R0,R0为非球面顶点曲率半径;r为非球面的径向半径,ai为第i次径向坐标项系数,在本次设计中选取r4、r6、r8和r10项对应系数作为优化变量,其余系数为0。

其次,应用设计软件相关优化操作数来控制系统设计性能指标[14,15],如操作数EFFL控制系统光焦度,并构建系统优化操作数来对系统各类像差进行有针对性不断反复优化,最终设计得到一款满足表1给出的系统各项性能指标的离轴四反光学系统。该光学系统结构及光路图如图4所示,对应系统中反射镜曲率半径及间隔参数由表4给出,各块反射镜的偶次非球面系数由表5给出。

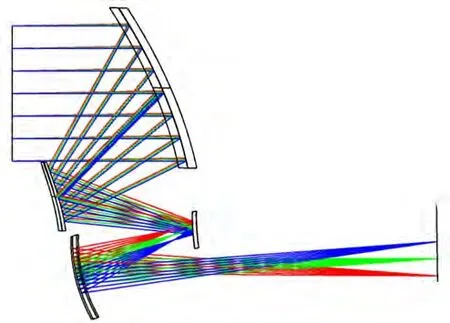
图4 离轴四反光学系统结构及光路图Fig.4 Structure and optical scheme of off-axis four-mirror reflective optical system

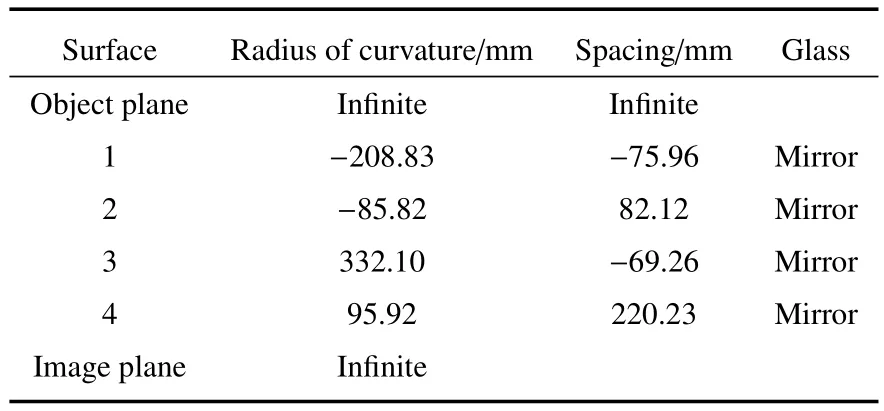
表4 离轴四反光学系统结构参数Table 4 Structural parameters of the optimized off-axial four-mirror reflective optical system

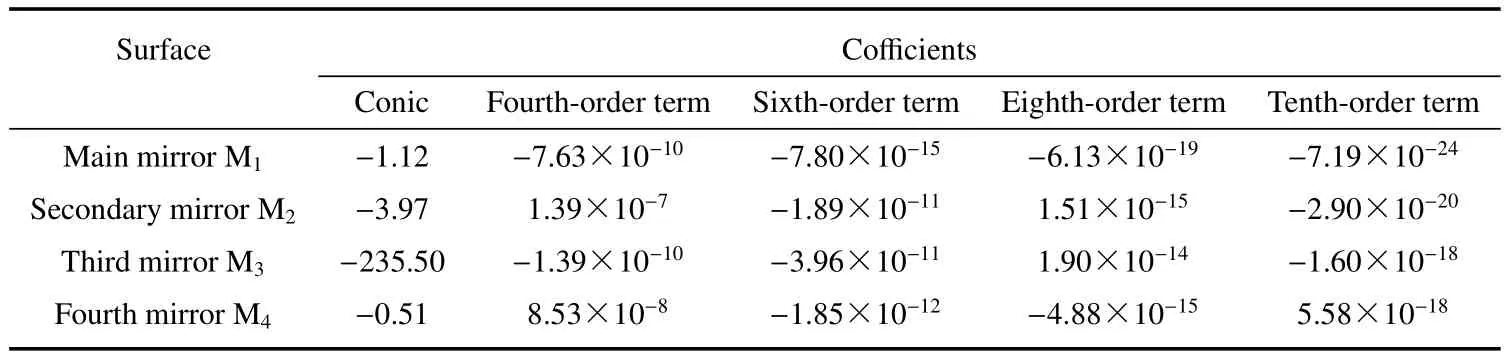
表5 各块反射镜非球面系数Table 5 Aspherical coefficients of each reflective mirror

2.2 离轴四反光学系统像质评价及分析

调制传递函数(MTF)是光学系统成像质量的综合评价指标,从表1给出的系统性能指标能计算出离轴四反光学系统的奈奎斯特频率为1000/(2×20)=25 lp/mm。并且该离轴四反光学系统是非对称系统,因此在系统视场范围选取视场角时需要考虑正负两个方向,即选取-0.5°、-0.354°、0°、0.354°和0.5°这5个视场角来评价系统成像性能,得到优化设计后离轴四反光学系统调制传递函数(MTF)曲线如图5所示。从图5中可以看出,系统在子午和弧矢方向上全视场MTF值在奈奎斯特频率25 lp/mm处分别均大于0.35和0.48,并且系统在选取的5个视场角情况下的点列图均方根半径RMS值分别为13.236、10.744、9.617、8.287和7.464µm,各视场RMS最大值小于探测器单元像素尺寸20µm。由以上分析结果可知所设计的系统具有较好的成像质量。

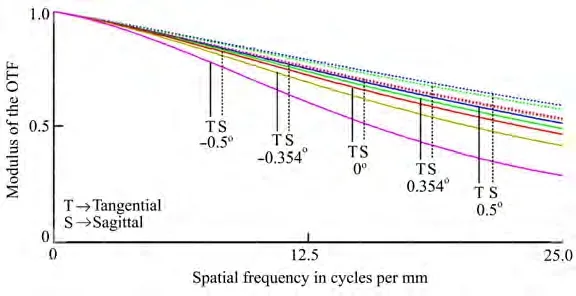
图5 离轴四反光学系统调制传递函数曲线图Fig.5 MTF curve diagram of off-axis four-mirror reflective optical system

2.3 公差分析

公差分析是光学系统从设计走向工程应用必不可少的步骤,公差制定的合理性直接影响光学系统总体性能水平。此处在完成了对离轴四反光学系统的设计后,对其制定了宽严适当的公差分配结果。由于它是反射式光学系统,只需要考虑加工和装调误差,因此在公差分析过程中,该系统需要分配的公差主要包括四块反射镜的曲率半径、各镜面的二次曲面系数及表面不平整度的误差;四块反射镜沿光轴方向的位移误差以及各反射镜绕X、Y轴的旋转倾斜误差。公差分析采用灵敏度分析方法,以系统在奈奎斯特频率25 lp/mm处的MTF值作为设计性能评价指标,使用后截距作为系统补偿量,结合Zemax光学设计软件反复不断对光学系统样本进行加工装调模拟,并根据结果分析给出公差范围对系统成像品质的影响情况,最终得到了一组系统公差合适的分配结果,具体由表6给出,满足系统设计指标要求。

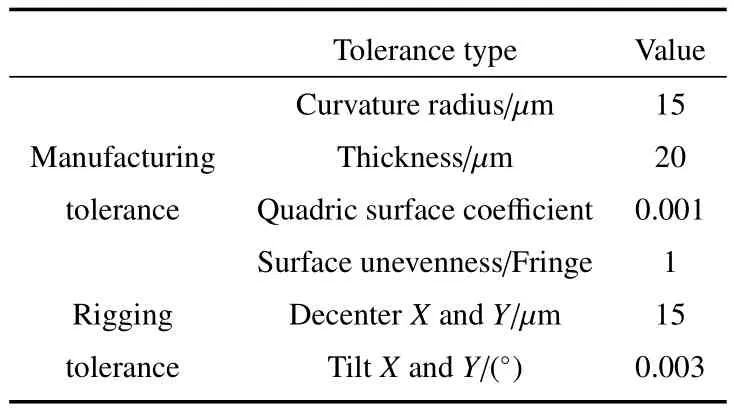
表6 离轴四反光学系统公差分配Table 6 Tolerance distribution of the optimized off-axial four-mirror reflective optical system

3 结论

基于同轴四反光学系统像差分析方法,构建了以均方根波像差为条件的系统成像性能评价目标函数,并引入了一种自适应变异概率的改进遗传算法对其进行求解,给出一种此类光学系统初始结构的确定方法；通过该方法确定同轴四反光学系统的相关结构参数,对系统反射镜进行偏心及倾斜处理,同时将系统中各块反射镜设定为偶次非球面来校正系统像差。应用上述方法设计了一种离轴四反光学系统,该系统具有结构紧凑、成像质量良好且公差范围适当等特点,同时能实现宽光谱和较大孔径成像,在空间光学系统中应该更广泛,为此类系统设计提供一种有效指导方法,具有一定的实际应用价值。