一种量子图像伪彩色编码方法

臧一鸣,朱尚超,魏战红,刘志飞,林小竹,孙文韬

(北京石油化工学院信息工程学院,北京 102617)

0 引言

量子计算机利用量子态的叠加性、相干性和纠缠性等独特的计算特性,展现了优越的存储和并行计算性能,为计算机的发展带来了希望[1]。同时IBM的IBM Q[2]与本源量子的本源量子云等量子云平台与编程框架为量子计算机的发展带来了活力。量子计算的分支-量子图像处理激起了学者的兴趣。量子图像处理是指利用量子力学特性来存储、分析及处理图像数据,包括图像表示和量子图像处理算法。

目前,量子图像表示模型主要有:Qubit Lattice模型[3],Real Ket模型[4],Entangled Image模型[5],量子图像的灵活表示(FRQI)模型[6],新型增强量子图像表示(NEQR)模型[7],量子彩色图像多通道表示(MCQI)模型[8],新型极坐标变换量子图像表示(QUALI)模型[9],用角度信息来存储颜色和坐标的QSMC&QSNC模型[10],任意量子叠加态的多维量子彩色图像表示(NAQSS)模型[11],通用量子图像表示(GQIR)模型[12],新型彩色量子图像表示(NCQI)模型[13],量子图像位平面表示(BRQI)模型[14]等。

此外,量子图像处理算法不断涌现,如几何变换[15]、特征提取[16]、图像增强[6]、边缘提取[17]、图像置乱[18,19]和形态学图像处理[20]都有其对应的量子版本。目前,量子图像各个方向的研究发展不均衡,有关量子图像增强算法的研究成果较少。2015年,Jiang等[12]提出了一种量子图像伪彩色编码方法,通过构建颜色映射表将灰度图像映射成彩色图像。

本文提出的量子图像伪彩色编码方法对热金属码分段函数进行量子化,并给出了该量子算法的量子线路。该方法的优点有:一方面,与经典伪彩色算法相比,不仅可以减少存储资源的占用,而且算法运行时间指数级降低;另一方面,与现有量子图像伪彩色编码方法相比,不需要人为设计颜色映射表并不需要构建与之对应的量子数据,可以减少量子资源的使用、降低空间复杂度,并且对连续的灰度值可以产生连续的彩色。对本文所提量子算法在经典计算机上用Matlab2020a进行了仿真实验,验证了其有效性。

1 量子图像的表示

GQIR量子图像表示模型可以存储任意大小为M×S的量子图像,存储Y坐标信息中的M个数据需要m量子比特,存储X坐标信息中的S个数据需要s量子比特,其中m和s分别满足

所以GQIR在存储大小为M×S的图像时需要m+s量子比特来存储位置信息。其中有效存储图像位置信息是M×S,冗余像素位置信息是2m×2s-M×S,如图1所示,其中白色部分为图像位置信息,阴影部分为冗余像素位置信息。冗余像素的颜色信息部分始终保持为|0〉。

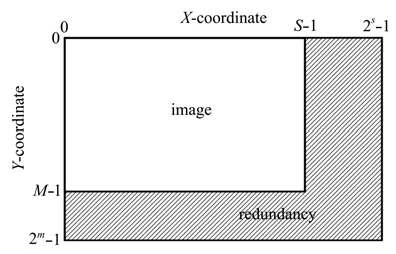
图1 GQIR表示模型Fig.1 The representation model of GQIR

GQIR表示模型可表示为

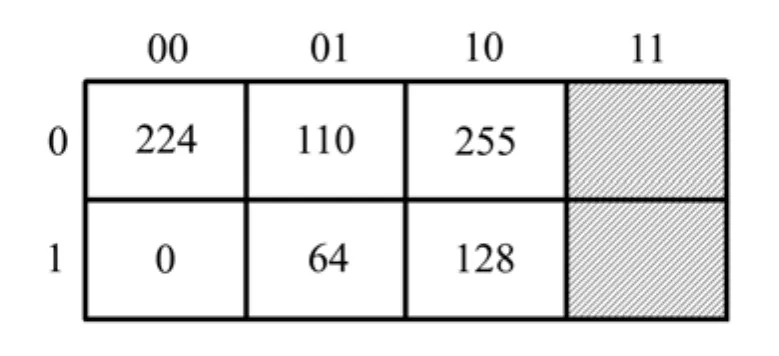
图2 GQIR模型表示下2×3的灰度图像Fig.2 Grayscale image of size 2×3 represented by GQIR model

图2给出了一个2×3的灰度图像,其GQIR表示为

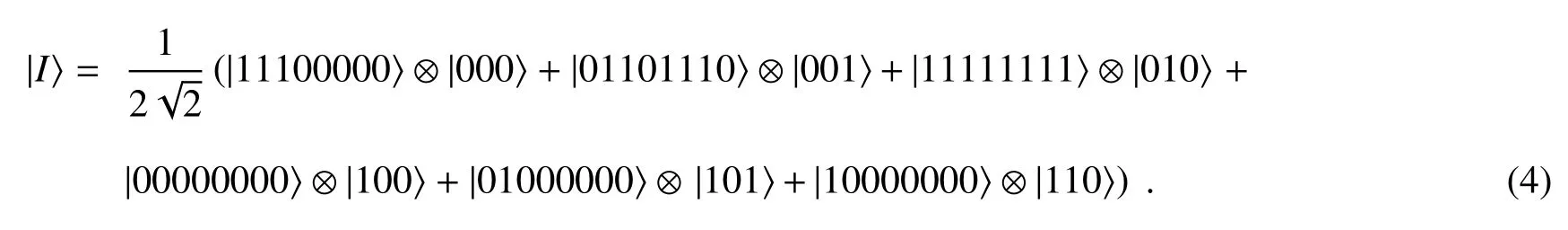
由(1)、(2)式可知

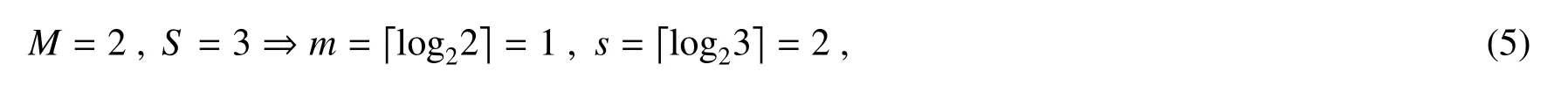
由(5)式可见,存储2×3的灰度图像总共需要3量子比特。而实际上,只有6个像素位置(Y=0/1,X=00/01/10)是有用的,其余两个像素位置是冗余的。

2 量子图像伪彩色编码

2.1 经典灰度级-彩色变换法

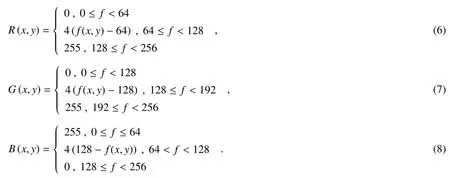
本研究用到的是热金属码,依据金属温度的变化,主要将图像颜色分为蓝色、红色和黄色三个部分,其中蓝色代表低温物体、红色代表中温物体、黄色代表高温物体,各部分之间实现线性的颜色过渡。热金属码灰度值与RGB彩色值的对应关系如图3所示。

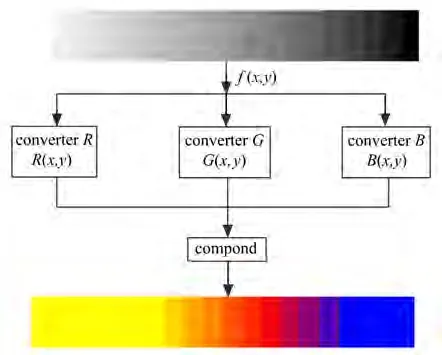
图3 热金属码中灰度值与RGB彩色值的对应关系Fig.3 The corresponding relationship between the gray value and the RGB color value in the hot metal code

2.2 量子减法器模块QSB

参考经典数字逻辑电路中全减器真值表以及逻辑电路的设计,引入了量子减法器的量子线路模块QSB,如图4所示。其中|a〉是被减量子位,|b〉是减量子位,|c0〉是量子借位输入位,|d〉是差量子位,|c1〉是量子借位输出位。

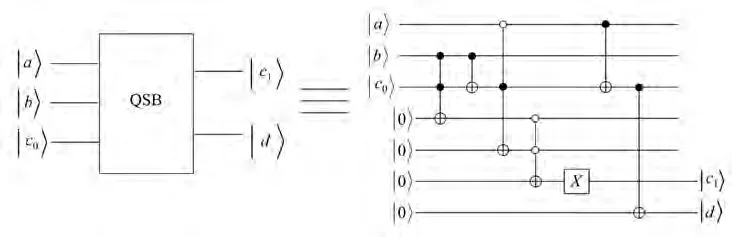
图4 QSB的量子线路设计Fig.4 Quantum circuit design of QSB

2.3 量子图像伪彩色编码的算法描述

以热金属编码分段函数为主要研究对象,设计了量子图像伪彩色编码方法,彩虹编码也可以根据此编码方法的原理进行设计。

量子图像伪彩色编码的输入为GQIR表示的量子图像|I〉,包括量子图像位置信息|YX〉和颜色信息|CYX〉,存储|CYX〉需要q量子比特。输出为伪彩色图像|J〉,颜色信息为|DYX〉,存储|DYX〉需要p量子比特。在本算法中q=8,p=24,其中表示红色,表示绿色,表示蓝色。

量子图像伪彩色编码算法描述如表1所示,其中输入为灰度图像|I〉,输出为伪彩色图像|J〉,分别定义为

表1 量子图像伪彩色编码的算法描述Table 1 Description of quantum image pseudo color coding algorithm

2.4 量子图像伪彩色编码的算法实现

伪彩色图像的存储总共需要p量子比特。本算法中p=24,首先初始化24量子比特全部为|0〉态,即

2.4.1 量子R变换器量子线路模块

在量子R变换器中,定义算子W1

定义算子W2

定义算子W3

量子R变换器量子线路模块如图5所示。

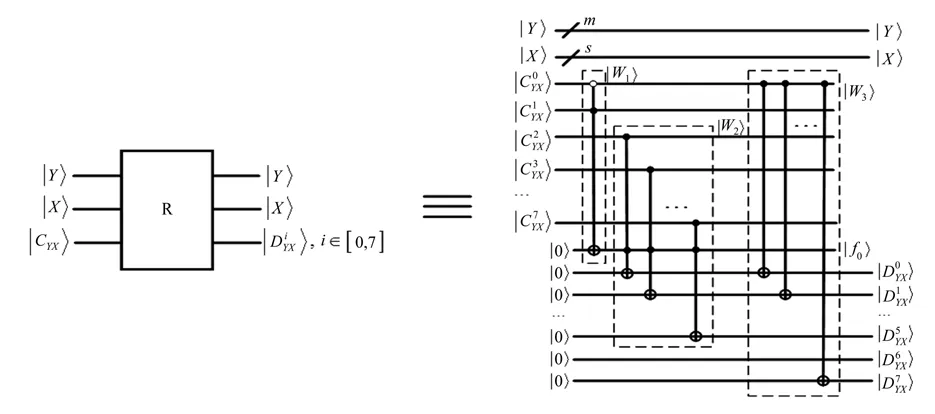
图5 量子R变换器量子线路模块Fig.5 Quantum circuit module of quantum R converter

2.4.2 量子G变换器量子线路模块

定义算子W4

定义算子W5

定义算子W6

量子G变换器量子线路模块如图6所示。

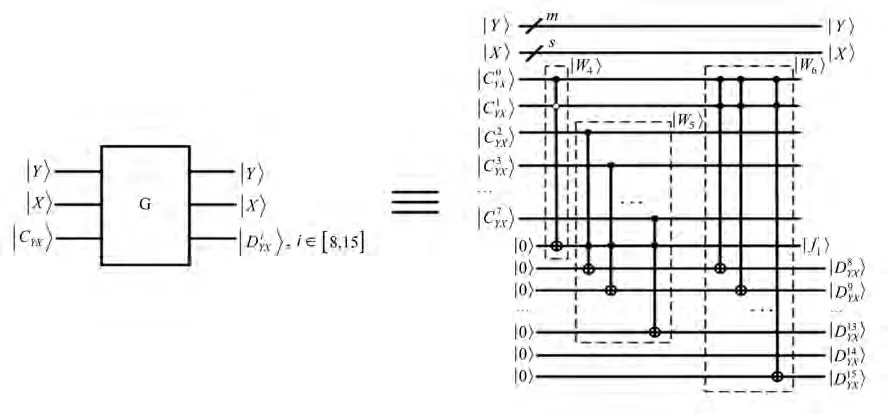
图6 量子G变换器量子线路模块Fig.6 Quantum circuit module of quantum G converter

2.4.3 量子B变换器量子线路模块

定义算子W7

定义算子W8

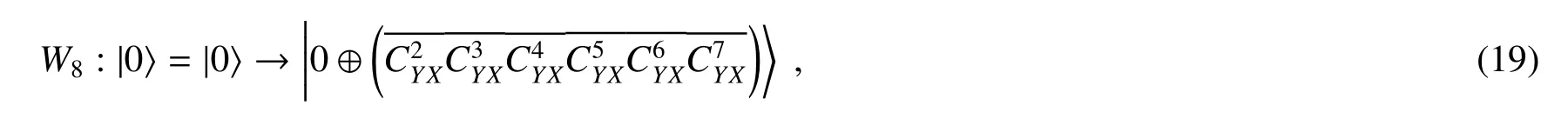
定义算子W9

定义算子W10

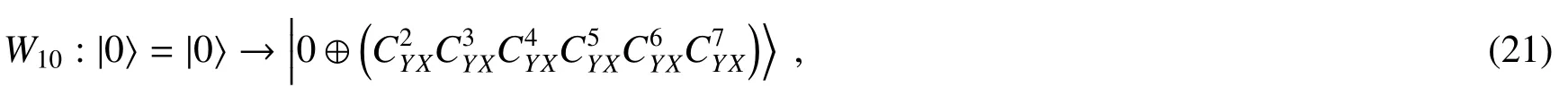
把目标量子位称为|f3〉。

定义算子W11

把目标量子位称为|f4〉。

算子W12为受控6位量子减法器f4-W12,需要调用QSB模块6次。其中|f4〉为控制位,W12为受控算子,有

为6位量子减法器中第j位的差量子位值(从低位算起,图7中从左往右数),具体实现如图7所示。在中,被减量子位为|0〉,减量子位为借位输入 (输出)位为 |c1〉,前一级的借位输出连接到下一级的借位输入,最低位即的借位输入位为|0〉。

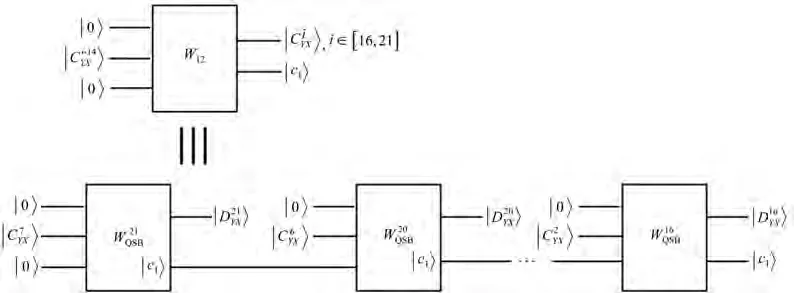
图7 6位量子减法器的实现Fig.7 Realization of 6-bit QSB

量子B变换器量子线路模块如图8所示。

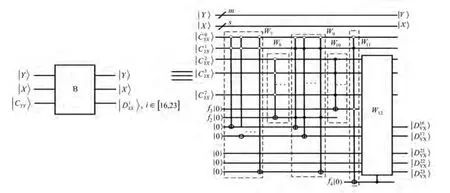
图8 量子B变换器量子线路模块Fig.8 Quantum circuit module of quantum B converter

2.4.4 量子图像伪彩色编码量子线路总体设计

算子W1～W3实现了量子R转换器,算子W4～W6实现了量子G转换器,算子W7～W12实现了量子B转换器。量子图像伪彩色编码量子线路总体设计如图9所示。

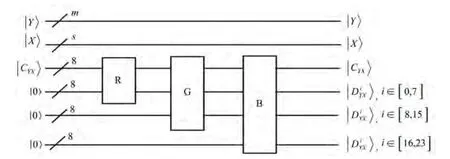
图9 量子图像伪彩色编码量子线路总体设计Fig.9 General design of quantum image pseudo color coding quantum circuit

3 复杂度

3.1 空间复杂度

经典伪彩色灰度级-彩色变换法的空间复杂度为(p+q)MS。在基于灰度级-彩色变换法的量子图像伪彩色编码中,输入为量子图像,占用量子比特;输出为量子伪彩色图像,存储颜色信息需要p量子比特。由图5可以知道量子R变换器需要1个辅助量子比特;由图6可以知道量子G变换器需要1个辅助量子比特;由图4、图7和图8可以知道量子B变换器中使用到了6次QSB量子减法器模块,其中6次QSB减法器模块需要1个量子比特的初始借位和1个量子比特的公用被减量子位|0〉,此外仍需要24个辅助量子比特用作中间计算。由于QSB模块受控制位|f4〉控制,因此需要额外的1个辅助量子比特来分解3 CNOT门。量子B变换器总计需要27个辅助量子比特。所以量子图像伪彩色编码的空间复杂度为

3.2 时间复杂度

在经典伪彩色灰度级-彩色变换法中,图像的颜色是逐个像素改变的,对于每一个像素,都需要分别判断灰度值所属区间并通过R、G、B转换器计算相应R、G、B值。因此算法复杂度是3MS。

在量子计算中,量子网络复杂度取决于所使用CNOT门和1位量子门的数量。一个t-CNOT门等价于2(t-1)个Toffoli门和1个CNOT门(t＞2),1个Toffoli门等价于6个CNOT门、10个1位量子门[21]。1个t-CNOT门的量子网络复杂度为32t-31(t＞2),如果t-CNOT的控制位t-1个为“°”,如图10所示,t-CNOT门的量子网络复杂度为32t-31+2(t-1)=34t-33(t＞2)。

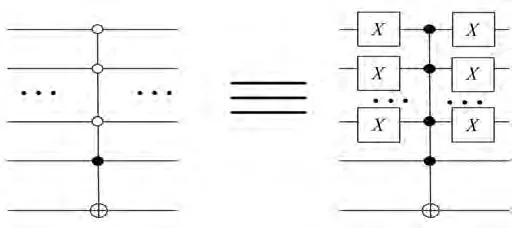
图10 t-CNOT的控制位包含“°”Fig.10 The control bits of t-CNOT contains“°”

根据图5,W1的量子网络复杂度为18;W2的量子网络复杂度为96;W3的量子网络复杂度为8,所以量子R转换器的量子网络复杂度为122。根据图6,量子G转换器模块W4的量子网络复杂度为18;W5的量子网络复杂度为96;W6的量子网络复杂度为128,所以量子G转换器的量子网络复杂度为242。根据图4、图7和图8,量子B转换器模块W7的量子网络复杂度为144;W8的量子网络复杂度为173;W9的量子网络复杂度为536;W10的量子网络复杂度为161;W11的量子网络复杂度为69;量子减法器模块QSB的量子网络复杂度为250,W12为6位量子减法器,需使用6次受控QSB模块,量子网络复杂度为1500,量子B转换器的量子网络复杂度为2583。所以所提出的量子图像伪彩色编码的量子网络复杂度为2947。

图11给出了经典灰度级-彩色变换法和基于灰度级-彩色变换法的量子图像伪彩色编码分别处理像素为表4所示、色深为256(q=8)的图像时的算法复杂度比较。很明显可以看出,随着像素点的增多,所提处量子算法维持在2947这一常量级别,而经典算法时间复杂度按107量级增大。

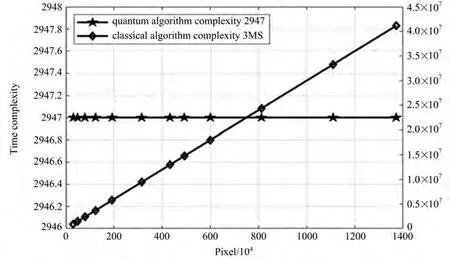
图11 经典算法和量子算法复杂度比较Fig.11 Complexity comparison between classical algorithm and quantum algorithm

4 经典计算机中的仿真实现

图2所示6个像素点的灰度图像经过所提出量子图像伪彩色编码方法处理后,得到的伪彩色图像如图12所示。当f(0,0)=224时,RGB=(255,255,0);当f(0,1)=110时,RGB=(184,0,72);当f(0,2)=255时,RGB=(255,255,0);当f(1,0)=0时,RGB=(0,0,255);当f(1,1)=64时,RGB=(0,0,255);当f(1,2)=128时,RGB=(255,0,0),与实验结果相吻合。验证了所提处算法的可行性。

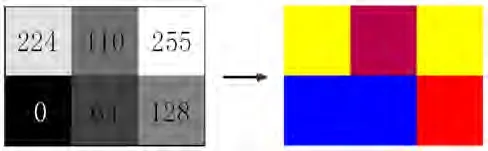
图12 伪彩色处理结果Fig.12 Result of pseudo-color processing

图13展示了一幅4张CHAOS脏器的灰度图像经过所提出热金属码量子图像伪彩色编码处理后的结果,由图可见处理后图像增强的效果较好,清晰度较高。

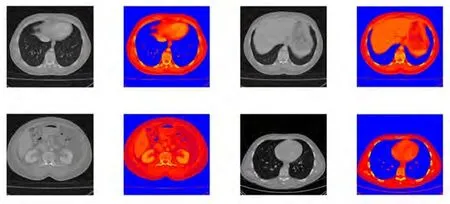
图13 CHAOS多脏器灰度图像热金属码伪彩色处理结果Fig.13 Hot metal code pseudo-color processing results of CHAOS multiple organs gray image

5 结论

提出了基于灰度级-彩色变换法的量子图像伪彩色编码方法。主要有两个方面的贡献:1)首次给出了灰度级-彩色变换法的量子算法版本。相比于密度分层法,灰度级-彩色变换法不需要人为创建颜色映射表,而是根据函数一一映射成R、G、B颜色分量。相比于经典算法,所提算法实现了指数级减少内存空间的占用和指数级降低算法复杂度;2)给出了所提出量子图像伪彩色编码方法的量子线路图。在量子计算机上将实现量子图像所有像素点的并行运算。