混合动力履带车辆机电联合制动控制

张伟， 刘辉， 韩立金， 刘宝帅， 张勋， 张万年

(北京理工大学 机械与车辆学院， 北京 100081)

0 引言

制动性能是体现履带车辆机动性的重要指标，随着履带车辆向高速化、重载化和智能化方向发展，混合动力与纯电驱动等新能源车辆技术逐步应用于履带车辆领域。引入电驱动技术的履带车辆采用机电式联合制动系统，与传统履带车辆机械式和机- 液混合式[1]制动系统相比，机电联合制动系统不仅能够回收制动能量、提高能源利用率，而且能显著减小机械制动器的磨损与热负荷，从而延长使用寿命[2-3]，同时该制动方式控制灵活、响应快，对改善制动过程中普遍存在的履带滑移现象、提升履带车辆的制动性和行驶安全性具有较大应用潜力，特别是在泥泞、冰雪等路面上制动出现的履带打滑、主动轮抱死等失稳工况具有显著优势[4-6]。

机电联合制动系统能够满足高速、频繁、长时间和大制动力需求，相关研究对于行驶环境恶劣的履带车辆具有重要意义。目前，针对民用轮式车辆的机电联合制动研究较多，已研发出丰富的理论成果和应用技术[7-12]，但是针对履带车辆研究较少，主要集中在机电联合制动力矩分配控制策略方面。周秋君等[13]针对电传动履带车辆制动过程，分析了高、中、低速条件下电气制动、机械制动和机电联合制动的特性，提出理想三段式制动控制策略，改善了制动器的温升，延长了制动器的寿命。马田等[14]研究发现理想三段式联合制动策略存在制动时间过长的问题，摒弃高速纯电气制动的策略，提出改进的两段式机电联合制动控制策略。李峰等[3]针对三段式机电联合制动控制策略的不足，基于模糊控制思想，提出基于车速、踏板行程和电池荷电状态(SOC)等因素的机电联合制动力分配模糊控制策略，该策略具有更好的制动效能，但未考虑电机制动力矩的饱和因素，存在动态协调失准隐患。曾庆含等[15]充分考虑电机制动能力约束，基于驾驶员意图识别，改进了模糊控制策略。但该策略以电气制动分配系数为参考值，以机械制动力补偿电气制动，存在响应时间不匹配问题，动态波动较大。张晓辰等[16]同样采用模糊控制策略，为解决传统门限控制策略中门限参数漂移适应能力差、模式切换频繁、能量回收率低等问题，采用粒子群优化算法对模糊隶属度函数进行了优化。生辉等[17-19]针对高速电驱动履带车辆，分析了机械制动器、电机和电液缓速器3种制动系统制动转矩的动态特性，提出前馈- 反馈动态协调控制算法，解决了扰动情况下多系统联合制动的力矩波动问题。此外，陈朝萌等[4]、张舒阳[5]等、Zhang等[6]关注履带车辆的制动稳定性，分析履带滑移问题，研究了在履带- 地面附着极限条件下的机电联合制动控制策略，有效减少了主动轮抱死和履带过大滑移现象。

以上研究主要针对双侧电驱动履带车辆，对于双模混联式混合动力履带车辆机电联合制动的研究尚未涉及。本文以装配机电复合传动(EMT)系统的某型重载混合动力履带车辆为对象，进行机电联合制动智能控制理论研究，充分考虑地面附着条件、运行工况、电机状态等约束条件，兼顾制动安全性、制动稳定性、能量回收效率以及路况适应性等控制目标，设计了一种以电机制动能力饱和度为控制目标的全工况机电联合制动控制策略，并进行了仿真验证。

1 系统模型

1.1 双模混联混合动力履带车辆系统构型

双电机混联式混合动力履带车辆的传动系统结构[20]如图1所示。该型混合动力履带车辆传动系统由发动机、电池组、双驱动电机、前传动、离合器、制动器、行星齿轮组机构等组成。图1中，CL为离合器，BK表示制动器，k1、k2、k3为行星轮系参数。车辆参数如表1所示。

图1 前传动及耦合机构系统结构Fig.1 Structure of front transmission and coupling mechanism

通过离合器和制动器的状态切换组合，可以实现多种驱动模式，其中混合驱动模式有两种，分别为电动无极变速1(EVT1)模式和电动无极变速2(EVT2)模式。混合驱动模式下发动机、电机、离合器状态如表2所示。

表1 双模混联混合动力履带车辆基本参数Tab.1 Basic parameters of dual-mode hybrid tracked vehicle

表2 混动模式下部件状态Tab.2 Component status in hybrid mode

1.2 整车纵向动力学模型

履带车辆制动过程受力如图2所示。图2中，v为车速，Fw为空气阻力，Ff为滚动阻力，Fb为制动阻力，Fp为坡道阻力，Fn为履带接地面法向力，α为坡度角，G为整车重力，其中G=mg，g为重力加速度。

图2 履带车辆纵向受力分析Fig.2 Longitudinal force analysis of tracked vehicle

因此有

(1)

式中：Ω为旋转质量转换系数；

(2)

f为滚动阻力系数，由试验测定，A为履带车辆正投影面积，CD为空气阻力系数。

1.3 行走系统动力学模型

假设制动过程中履带是柔软的不可拉伸的带，且履带上的所有的点都处于同一个平面内，如图3所示。图3中，Tb为主动轮制动力矩。

图3 制动过程履带受力分析图Fig.3 Track force diagram during braking

地面制动力可简化为履带与主动轮之间的相互作用力，则履带车辆制动动力学模型为

(3)

式中：ωd为主动轮转速。若地面不打滑，则有v=rdωd。

联立(1)式～(3)式，可得

(4)

地面施加的制动力Fb并不能够无限增大，其上限主要是土壤抗剪切强度决定的。Fb的最大值与履带接地面法向力Fn的比值为地面附着系数μ，即

Fb≤μ·Fn

(5)

根据履带- 土壤接触动力学模型[5]，有

μ=(1-λ)μΔ+μv

(6)

式中：λ为履带滑动实际滑移率，λ=0时履带纯滚动，λ=1时履带抱死拖滑；μΔ为履带与地面间静摩擦系数，其最大值为μs，对应门限变形量为Δmax；μv为履带与地面动摩擦系数，其最大值和最大静摩擦系数相等，即μv_max=μs，对应相对速度us，在履带抱死拖滑时值为μd，对应相对门限速度为ud。其中，各参量表达式为

(7)

ur为履带接地段相对地面速度。当ur=us时路面附着系数μ有最大值。典型地面附着系数试验数[4]如图4所示，可见μ峰值区间位于λ值25%～30%区间。

图4 履带车辆典型地面附着系数- 滑移率曲线Fig.4 Common ground adhesion coefficient-slip ratio curve

1.4 驱动系统模型

机械制动力矩控制器及液压系统动态响应模型可以近似为1阶惯性系统：

(8)

发动机及其控制器可简化为转矩响应传递函数模型[20]为

(9)

图5 发动机转矩模型辨识试验(ωe=2 400 r/min)Fig.5 Engine torque model identification test(ωe=2 400 r/min)

面向控制的永磁同步电机模型可简化为1阶传递函数[21]。电机动态响应转矩为

(10)

式中：τm为转矩响应时间常数；Tm_com为目标转矩；Tmm_max为驱动工况最大转矩；Tmg_min为发电工况最大转矩；ωm为电机转速。

1.5 传动系统模型

动力耦合及变速机构由多个行星排、离合器、前传动、侧传动等组成，是2自由度惯性耦合系统。设行星机构的特性参数为k1、k2，根据图1中行星轮系的连接关系，EVT1和EVT2模式稳态工况下耦合机构静态模型可分别由(11)式和(12)式描述：

(11)

(12)

式中：ωA、ωB、ωi、ωo分别为电机A、电机B、输入轴和输出轴转速；TA、TB、Ti、To分别为电机A、电机B、输入轴和输出轴转矩。

由行星轮系运动传递关系，可得EVT1和EVT2模式下的系统动态模型分别为(13)式和(14)式：

图6 电机制动力特性Fig.6 Motor braking force characteristics

(13)

(14)

发动机、电机A、电机B工况约束如下：

(15)

式中：ωe,min、ωe，max分别为发动机最小转速和最大转速；Te，min、Te，max分别为发动机工作转矩限值；ωm0、ωm,max分别为电机基速和额定转速；ωκ、Tκ(κ=A、B)分别为两个电机的实际转速和转矩；Pm,max为电机最大输出功率。

联立(13)式、(14)式和(15)式，可计算出双电机复合制动特性如图6所示。

2 控制策略设计

为缓解机械制动器工作强度，同时回收制动能量，设计了可变分配比例的并联式复合制动结构[22]，如图7所示。并联式制动分配策略根据制动踏板计算总制动力，采用动态协调方法控制机械和电机两种制动系统之间制动力的分配。在低制动强度条件下电机制动力占比较大，随着制动强度升高，电机制动力进入饱和区，机械制动力占比增加。

图7 可变比例的并联式机电联合制动分配策略Fig.7 Braking distribution strategy with variable proportion

总制动力需求受履带- 地面最大附着力限制，行驶过程中地面附着系数的时变特性导致地面制动力峰值波动，路面附着系数不足时主动轮易抱死，导致履带拖滑车辆失稳。本文基于路面附着系数识别，提出电机制动饱和度模糊控制方法，设计分层制动控制器，以确保全路况条件下控制策略的有效性。

机电联合制动系统总体控制框架如图8所示。图8中，Tb1为驾驶员意图制动力矩，Tb2为最优滑移率控制输出力矩，k为电机制动饱和度，TA，max、TB，max分别为当前车辆运行状态下电机A、B可提供的最大制动力矩，未达到目标制动力矩的部分由机械制动器来进行提供。

图8 机电联合制动控制框架Fig.8 Control block diagram of electromechanical braking

上层控制器根据车辆状态和驾驶意图计算附着条件约束下全路况整车需求制动力，下层控制器基于模糊控制方法计算总电机制动力分配系数，并实时求解机械制动力矩，最后向执行器输出机电制动力矩控制指令。

2.1 总需求制动力矩

总制动力需求取决于驾驶员意图制动力矩Tb1、路面最大附着制动力矩Tbm和最优滑移率控制输出力矩Tb2三者之间的大小关系，即

Tb=min{Tb1,Tbm,Tb2}

(16)

驾驶员意图制动力矩由制动踏板开度决定，即

(17)

式中：δ、δ0、δmax分别为制动踏板实际行程、最小有效行程和最大有效行程。

由(5)式可知，路面最大附着制动力矩Tbm为

Tbm=mgμ

(18)

针对路面附着不足导致履带滑移失稳问题，采用滑模变结构控制算法进行滑移率控制，计算最优滑移率控制输出力矩Tb2。

选取滑模变结构切换函数为

Θ=λ-λobj

(19)

式中：λobj为目标滑移率，当路面种类不变时λobj为常数。

履带滑移率为

(20)

联立(16)式和(17)式，并对(16)式求导，可得

(21)

为缩短趋近时间、减小抖振现象，采用幂次趋近率和等速趋近率相结合的混合趋近率[23]如下

(22)

式中：ε表示系统运动点趋近切换面的速率，ε>0；1>α>0；sat(·)为饱和函数；电机制动饱和度k定义如下，

(23)

Tm为实际输出电机制动力矩。

由(3)式可写出如下关系式：

(24)

(24)式代入(21)式，与(22)式联立，可求解最优滑移率控制输出制动力矩Tb2，得到

(25)

2.2 机电联合制动分配策略设计

基于双电机制动性能边界及电机制动饱和度设计机电联合制动控制策略。以制动强度z、SOC、车速v作为输入，电机制动饱和度k作为输出，制定控制规则如下：

1)紧急制动时，目标制动力矩大，采用机电复合制动，尽可能多地提供制动力矩；中度制动时，电机制动饱和度稍大，可充分回收制动能量；轻度制动时，目标制动力矩较小，可单独采用电机制动。

2)当SOC较低时，尽量使用电机制动充电；当SOC水平较高时，应减少或停止电机制动。

3)当车速较高时，机械制动器摩擦剧烈，为减轻机械制动器使用压力、避免热衰退，电机制动保持较高饱和度；当车速较低时，EVT1模式发电功率小，回收制动能量有限，为保证制动可靠性，需要降低电机制动饱和度。

将制动强度z、车速v、SOC和电机的制动饱和度k分别进行归一化，并分割为3个、5个、4个、5个语言变量，论域为[0，1]。由此得到分割后的变量模糊集合如表3所示。

表3 变量模糊集合Tab.3 Variable fuzzy sets

基于上述3个基本原则，考虑双电机复合制动特性，优先保证制动性能，并根据当前情况尽可能减少机械制动器载荷，同时提升制动能量回收率，根据表3可制定模糊规则60条。

3 控制参数识别与优化

3.1 路面附着系数识别

在非公路条件下，路面附着条件变化频繁，地面最大制动力估计的准确性依赖于路面附着系数的辨识精度。本文采用扩张型状态观测器[24]识别路面附着系数μ。

对于线性控制系统

(26)

式中：X为状态变量；U为系统输入；Y为系统输出；A、B、C分别为系统矩阵、输入矩阵和输出矩阵。

构造出以下新的系统

(27)

式中：Z为观测器状态变量；L为观测器增益矩阵。

若存在矩阵L，使矩阵(A-LC)为李亚普诺夫稳定矩阵，则状态Z可以估算原系统状态变量X。系统(26)式可作为原系统(23)式的状态观测器，写作

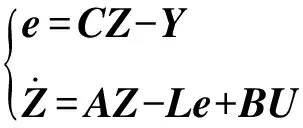
(28)

式中：e为系统的输出误差。

由(24)式履带车辆动力学模型，有

(29)

(30)

μ为非线性变化的量，可得非线性系统

(31)

由(28)式可得如下形式扩张型状态观测器[25]

(32)

令l1=-β1φ1(e),l2=-β2φ2(e)，β1、β2为观测器的增益系数，φ1、φ2为连续函数。则(32)式变为

(33)

当eβ2φ2(e)≥0且eβ2φ2(e)≥0时，可以确保观测器的输出信号z1、z2分别为x1、x2的观测值。

为避免高频震颤现象，将函数φχ(e)(χ=1，2)取为在原点附近具有直线段的连续幂函数fal(e，αχ，γ)，

(34)

式中：γ为线性段的区间长度。

扩张型状态观测器(33)式变为

(35)

故有

(36)

可计算得到路面附着系数的估计值为

(37)

在建立扩张型状态观测器的基础上，需要选取α1、α2、β1、β2等参数，αχ按(38)式选取

(38)

在fal函数中，一般取γ=5h，h为系统仿真步长，h的大小与被扩张状态的幅值M相关，按照h=0.25M-1进行取值。由(38)式可得α1=1，α2=0.5，M=2mgrd/J，故有

(39)

利用带宽的概念，使用二项式的展开式系数来确定状态观测器的增益参数[26]；根据扩张状态观测器参数与斐波那契数列之间的关系[27]，并给出了h-1的幂次形式经验公式如下：

(40)

在实际应用中，由于具体研究对象和系统的不同，通常把经验公式计算的值作为参考值，再通过数值仿真在参考值附近寻找合适的参数。优化参数后取β1=300，β2=2 000。

在实际过程中，履带车辆行驶的路面往往是多种复杂道路，例如由耕地路面跨越柏油路面再进入耕地路面这种附着系数突变的工况，为验证设计观测器的有效性，在附着系数突变的坚实土壤路面工况下进行制动仿真分析，取初始车速v0=36 km/h，仿真结果如图9所示。

图9 变路面附着系数观测结果Fig.9 Observation results of variable road adhesion coefficient

由图9可知，在附着系数突变的路面上所设计观测器能准确识别路面附着系数，分别在0.28 s、3.24 s、6.26 s处到达稳定并收敛至实际值0.5、0.7和0.3，平均响应速度为0.26 s，路面附着系数观测值和路面附着系数实际值误差小，表明该算法识别速度快，精度高。

3.2 分配策略参数优化

将制动强度z、车速v、电池SOC 3个参数采用三角形隶属度函数，对于模糊控制器的输出电机制动饱和度k的隶属度函数采用高斯型函数。将隶属度函数参数化，如图10所示。

采用遗传算法分别对图10中制动强度z、SOC、车速v的隶属度函数参数a1～g1，a2～i2，a3～f3等参数进行优化。

选取电机制动饱和度k值的累积作为目标函数，种群数目设置为200，适应度函数选取为

(41)

遗传算法优化隶属度函数流程如图11所示。

图10 隶属度函数参数化图Fig.10 Parameterization of membership function

图11 遗传算法优化隶属度函数流程图Fig.11 Flow chart of membership function optimization based on genetic algorithm

选择操作采用锦标赛法，在种群中抽取数量为n的个体进行比较，获得适应度最高的个体，将其遗传到下一代中，重复该操作使种群规模与初始规模一致。采用单点交叉方法，交叉概率取0.8。为增加种群的多样性，同时提高算法的局部搜索能力变异操作，采用自适应变异方法。优化结果如图12所示。

图12 遗传算法优化结果Fig.12 Optimization results of genetic algorithm

由图12可知，在第82代左右到达稳定，在达到150代最大迭代次数时停止迭代，此时第150代中个体最优适应度为41.757，种群平均适应度为41.757。优化后的隶属度函数结果如表4所示。

表4 隶属度函数优化结果Tab.4 Optimization results of membership function

优化后隶属度函数图形如图13所示。电机制动饱和度k随归一化车速- SOC、k随车速- 制动强度、k随SOC- 制动强度的变化如图14所示。

图13 优化后隶属度函数Fig.13 Membership function after optimization

图14 履带车辆机电联合制动模糊规则图Fig.14 Fuzzy rule diagram of electromechanical braking of tracked vehicle

4 控制算法验证

为了验证混合动力履带车辆机电联合制动控制策略的有效性和实时性，利用仿真实验及硬件在环平台进行验证。选择高速紧急制动工况进行模拟，制动初速度为85 km/h、制动踏板开度为95%。

仿真结果如表5所示，从中可见电机制动比例变化范围为4.3%～14.3%，电机制动比例平均值为8.96%，证明电机制动可以有效辅助机械制动，降低机械制动器使用强度。

表5 紧急制动仿真结果Tab.5 Simulation results of emergency braking

制动过程如图15所示。图15(a)表明经过4.5 s车速减为0 km/h，制动效果良好。制动力矩变化见图15(b)，电机制动力矩快速响应目标制动力矩，初始阶段机械制动力矩受作动器影响有0.25 s延迟；0.25 s以后，目标制动力超出当前车辆状态下地面最大制动力，总制动力目标按照最大地面制动力输出，整车滑移率逐渐上升(见图15(c))；0.4 s滑移率到达目标控制区域，目标制动力矩开始按照滑移率控制策略执行，总制动力矩小幅度波动。0.65 s时，整车滑移率开始稳定在0.27，总制动力矩保持稳定。

车辆在3.5 s时由EVT2模式切换至EVT1模式，电机制动力矩突变，电机A、电机B总制动力矩升高。初始阶段，电机制动饱和度k较大，这是由于电池SOC较低，车速较高，制动强度大。车速继续下降，EVT1模式下总的发电功率较小(见图15(d))，回收制动能量有限，为保证制动可靠性，电机制动饱和度变小。电制动饱和度变化趋势合理，与制定联合制动策略基本原则相符合，说明模糊控制规则设计合理。

图15 初速度85 km/h紧急制动仿真结果Fig.15 Simulation results of emergency braking (v0=85 km/h)

将仿真控制器算法通过代码自动生成，下载到快速原型控制器RaidECU中。将电机及其控制器、耦合机构，机械制动器等机械系统以及履带车辆和轮- 履- 路等动态模型下载到下位机系统，通过总线与控制器通讯。硬件在环实验结果如图16所示。

对比图16和图15可知，制动过程中，制动力矩和电机制动功率吻合较好，只在模式切换过程中出现较大波动，结果表明：所设计的全工况机电联合制动控制算法实时性较好，能快速响应制动需求，并有效回收制动能量。

图16 硬件在环实验结果Fig.16 Results of Hardware-in-the-loop test

5 结论

本文以混联式混合动力履带车辆为对象，研究全路况机电联合制动控制策略并进行了仿真验证。得出主要结论如下：

1)应用扩张型状态观测器理论设计路面附着系数观测器可以有效识别履带车辆路面动态附着系数。算法速度快，精度高，稳定可靠，所识别的路面附着系数可用于机电联合制动策略制定。

2)高速紧急制动仿真表明，制动开始0.5 s内滑移率稳定在最佳滑移率0.2左右，所设计的滑模控制算法可以有效控制低附路面上紧急制动工况的履带滑移率。

3)以电机制动能力饱和度为控制目标的机电联合制动控制算法充分考虑了制动强度、车速、电池SOC等因素对制动能量回收的影响，有效融合了能量回收效率和电机稳定性指标，解决了底层机械/电机制动力的协调分配问题。