测量不确定的充液航天器自适应鲁棒容错控制
宋晓娟,王宏伟,岳宝增
(1. 内蒙古工业大学机械工程学院,呼和浩特 010051;2. 内蒙古自治区特种服役智能机器人重点实验室,呼和浩特 010051;3. 西北工业大学航天学院,西安 710072; 4. 北京理工大学宇航学院,北京 100081)
0 引 言
现代大型航天器要求携带大量的液体燃料推进剂用于支撑自身机体完成一系列航天任务,例如太空在轨服务,航天器交会和对接,以及航天器编队飞行等。部分充液航天器的耦合系统为典型的未知动态欠驱动动力学系统,在描述被控对象及建立数学模型的过程中,由于含有一些未知因素和随机因素,从而导致被控系统有很强的不确定性,在建模过程中多以等效力学模型来描述液体燃料的晃动。文献[6]采用球摆模型推导了充液挠性航天器的耦合动力学模型,进而设计了自适应反步控制策略获得期望的控制目标。文献[7]利用质心面等效力学模型建立了充液航天器的耦合动力学模型,提出了一种抑制姿态振荡的补偿控制策略。文献[8]将液体燃料晃动等效为球摆模型,设计了自适应无源控制律完成充液航天器大角度姿态机动任务。文献[9]采用复合等效球摆模型研究了液体大幅度晃动的动力学建模问题,进而推导出了等效系统动力学方程。
由于航天器在轨运行不可避免地受到外部未知干扰和自身参数不确定的影响,一些学者将先进控制方法引入到航天器控制的研究中以获得到更好的效果,如滑模控制、自适应控制、反步控制和基于观测器的控制等。在设计控制律过程中,需进一步考虑执行机构和传感器的老化及故障问题,为了提高航天工程的安全性和可靠性,航天器闭环系统须考虑容错控制。文献[18]针对刚体航天器,采用积分类型的滑模面流形和自适应估计技术设计了鲁棒容错控制。文献[19]基于故障辨识技术设计了主动容错控制器获得期望的控制目标。文献[20-22]研究了刚体航天器存在干扰不确定和执行器故障的问题,采用变结构控制策略设计了鲁棒容错控制实现了良好的控制性能。文献[23-24]考虑刚体航天器系统中存在集总扰动和执行器故障的问题,然后基于干扰观测器的控制技术设计鲁棒容错控制器,保证了闭环系统的稳定性。
航天器姿态控制系统除了考虑执行器故障和干扰不确定性,还需考虑测量不确定问题。测量不确定会降低控制系统的动态特性和稳态精度。考虑航天器控制系统为典型的串级结构,文献[25]在反步控制策略中分别设计了范数自适应估计算法和层级模糊逻辑系统来补偿包含测量不确定的集总扰动。文献[26]针对刚体航天器存在集总扰动问题,将反步控制方法结合非线性干扰观测器设计了鲁棒控制策略。文献[27]在反步控制方案中设计了有限时间积分滑模干扰观测器,有效地估计系统的集总扰动,保证了航天器姿态机动稳定性。
本文研究了执行器失效和测量不确定的充液航天器大角度姿态机动鲁棒容错控制问题。主要内容包含:1)将部分充液贮箱内液体晃动等效为粘性球摆模型,利用动量矩守恒定律推导出航天器的耦合动力学模型,在此基础上考虑姿态的测量不确定性,进一步得到测量的动力学模型;2)采用时变变结构控制策略和自适应控制算法设计鲁棒自适应容错控制,其中自适应控制算法用于估计匹配集总扰动和失配集总扰动的范数上界,以及用于估计描述液体晃动的位移变量;3)与文献[25-27]利用反步控制方法设计的控制器相比,本文在变结构控制器的设计过程中考虑了测量不确定的估计和补偿算法,同时还考虑了执行器的失效故障问题;4)基于Lyapunov稳定性理论证明了容错闭环系统状态变量的一致有界性,实际的姿态和角速度会最终收敛到平衡位置的较小邻域内。

图1 充液航天器示意图和力学模型Fig.1 Schematic diagram and mechanical model of liquid-filled spacecraft
1 充液航天器动力学建模
1.1 航天器的数学模型
图1(a)展示了充液航天器,-坐标系表示航天器本体坐标系,-表示球摆坐标系。假设为刚体部分的质心,表示贮箱中心,也是球摆悬挂点,假设球摆悬挂点位于航天器本体坐标系的轴上,球摆的摆长为,球摆质量为,球摆相对于的位移矢量为,到的位移矢量为。假设球摆质量的位置在本体坐标系中表示为点,点和点连线上的一点C是主刚体和球摆所组成的系统的质心。C到的位移矢量为,C到的位移矢量为。点相对于球摆悬挂点的位移矢量为。
应用动量矩定理建立充液航天器动力学方程以及液体燃料晃动动力学方程

(1)
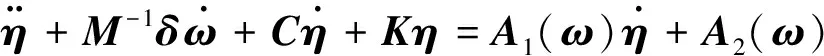
(2)
式中:为刚体航天器和液体燃料未发生晃动时总的转动惯量;为耦合矩阵;表示描述液体晃动的广义坐标矢量;表示施加在航天器上的控制力矩;()表示航天器受到的外部干扰力矩;为液体晃动质量的惯性矩阵;阻尼矩阵;刚度矩阵;和为方程中的高阶项。以上方程参数具体计算方法可参考文献[28]。
1.2 姿态运动学方程描述
考虑到克服参数奇异性的优点,本文使用欧拉四元数描述航天器姿态动力学方程,表示为
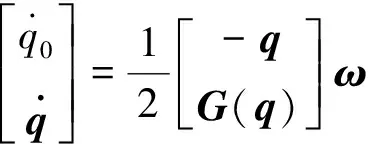
(3)

1.3 测量的动力学模型
考虑到航天器的姿态和角速度是由多个机载传感器测量得到的,同时由于空间中存在的复杂环境干扰,传感器的测量值一般是不确定的,通常含有噪音的成分。因此本文考虑的不确定性包括:未知的外部干扰(),航天器惯性矩阵的不确定Δ和航天器上姿态传感器的测量不确定,分别表示为Δ和Δ。测量的姿态四元数和角速度表示为
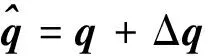
(4)

(5)
根据式(9)和式(11),可以得到
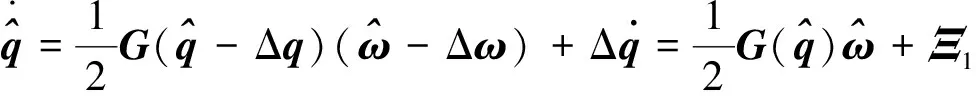
(6)


考虑航天器执行姿态机动任务,假设液体为小幅度晃动,可将式(1)和式(2)做线性化处理,即省略掉式(1)和式(3)中的高阶小量。为了控制系统推导方便,以及后文控制器设计方便,对于式(2)引入新的变量,将得到的方程结合假设1,同时考虑执行器存在失效故障的情形,测量的充液航天器动力学模型表示为

(7a)
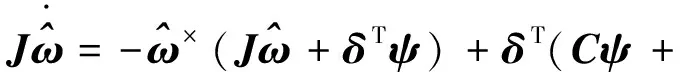
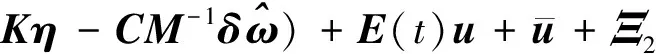
(7b)
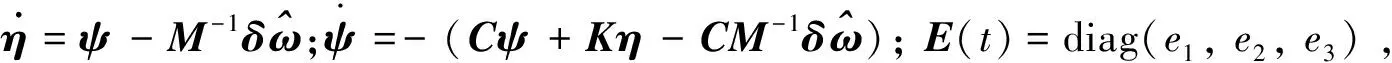

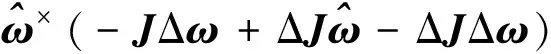
(8)
式中:=+Δ,Δ为参数不确定矩阵。
图2展示了本文的控制目标,其中期望的姿态和角速度等于零。考虑充液航天器姿态控制系统存在外部未知干扰,参数不确定,测量不确定和执行器部分失效的鲁棒控制问题,本文的控制目标为:
1)容错闭环系统中的所有状态向量信号都是最终一致有界的(GUUB)。

图2 控制器设计问题描述示意图Fig.2 Schematic diagram describing the controller design problems
2)测量的姿态和角速度是一致最终有界的,实际的姿态和角速度同时收敛到原点的较小邻域内。
3)性能指标定义为

(9)
是有界的,其中和为辅助变量,定义为

(10)

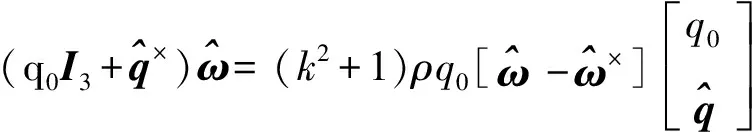
(11)
式中:()是待设计的时变函数;是正常数,其决定整个闭环系统的瞬态响应。
2 鲁棒容错控制律设计和稳定性分析
针对控制系统式(7)存在不匹配集总扰动和匹配集总扰动。本文将变结构控制策略结合自适应估计算法,提出了一种自适应鲁棒容错控制方法,用于实现上述控制目标。为了便于控制器设计,先考虑以下合理的假设:
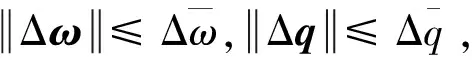

存在足够大的控制增益满足不等式
≥
式中:为待设计的控制参数。
假设3反映了故障信息的不确定性,因为0<≤1,所以假设3的合理性在于,可由两个极限值进行限定。假设4描述了足够大的控制增益抑制执行器故障的不确定性,该假设满足实际应用条件,从而实现期望的姿态机动任务。
考虑充液航天器姿态机动控制系统式(7)存在扰动不确定,测量不确定和执行器失效的问题,如果假设1~4得到满足,设计如下的自适应鲁棒容错控制律和自适应更新律,闭环系统的轨迹是全局一致最终有界的。


=1, 2, 3
(12a)
自适应控制律设计为
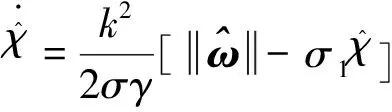
(12b)

(12c)
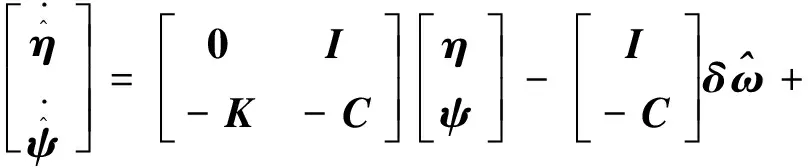

(12d)

考虑Lyapunov函数
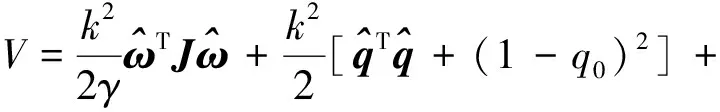
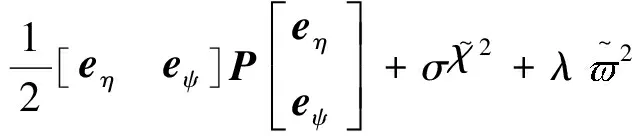
(13)
将式(13)对时间求一阶导数
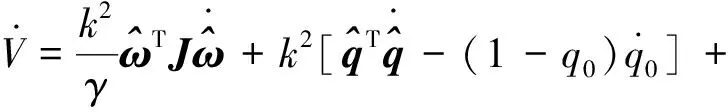
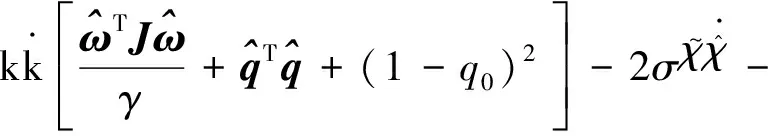


(14)
将式(7),(12a),(12b)和(12c)代入式(14)可得

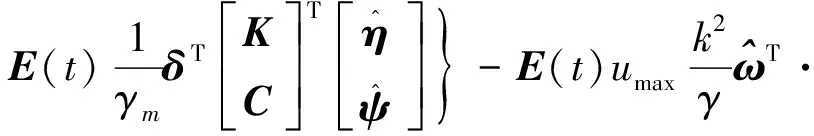






(15)
将式(12 d)代入式(15),并结合假设2和3,进一步简化可得


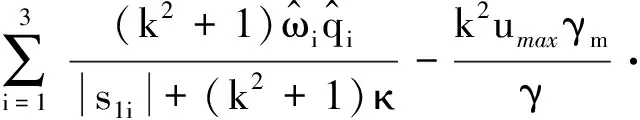

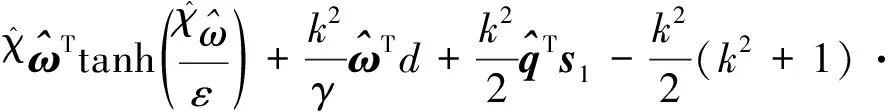
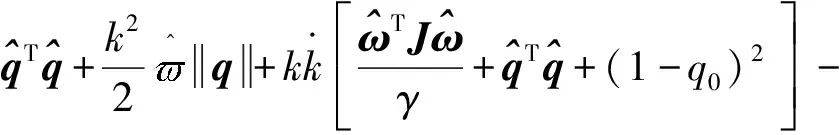
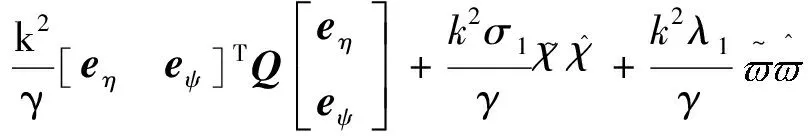
(16)

同时,注意到以下不等式成立
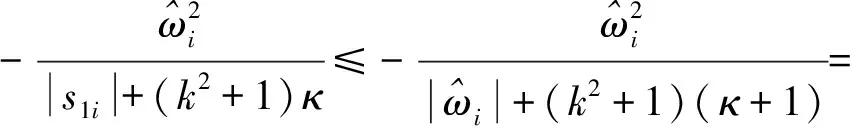
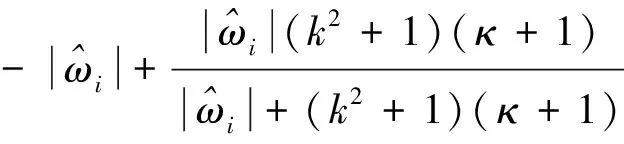
(17)
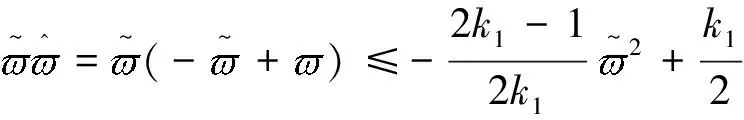
(18)

(19)
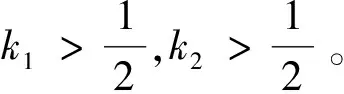
正切双曲函数具有性质
0≤||-||tanh()≤
式中:=02785;>0;∈。使用这个性质可以证明

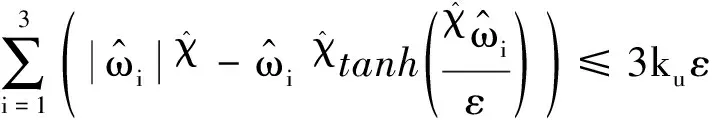
(20)
考虑式(10)和式(11),并且将式(17)~(20)代入式(16),进一步化简可得
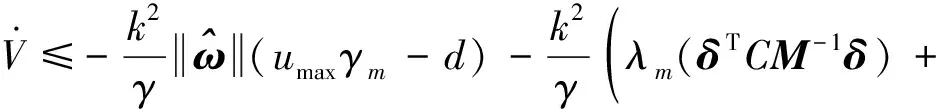

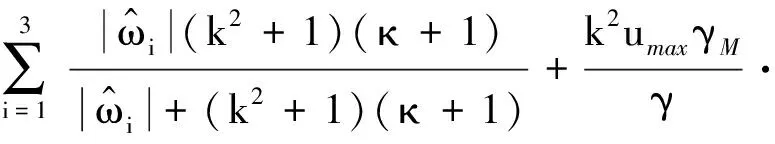




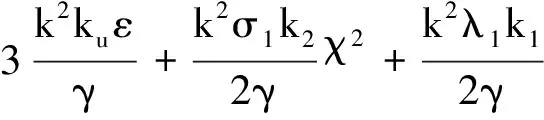
(21)
姿态增益的自适应算法设计为
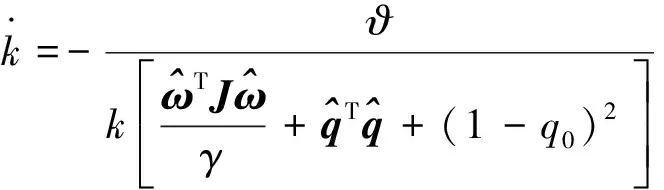
(22)

将式(22)代入式(21)得到
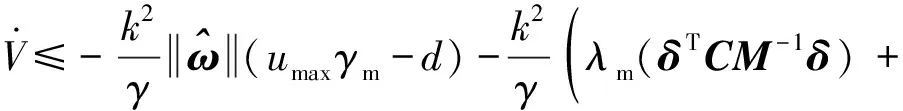


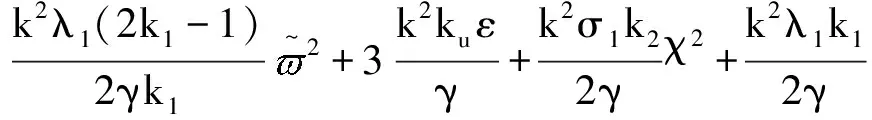
(23)
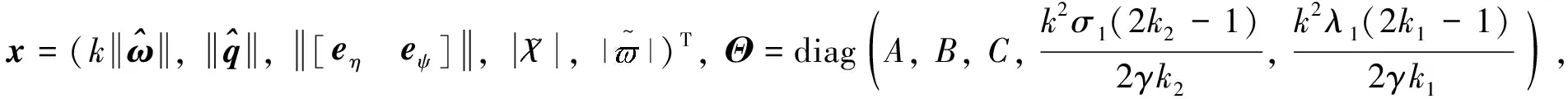
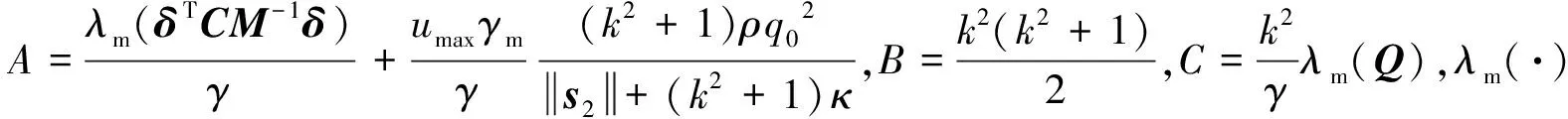
式(23)可以进一步写为

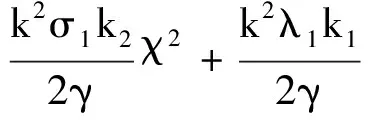
(24)
接下来,证明闭环系统的一致有界性。首先定义一个新的变量

根据式(13)定义的Lyapunov函数满足≤,并且以下不等式关系成立
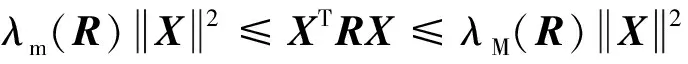
(25)

注意到如下不等式成立

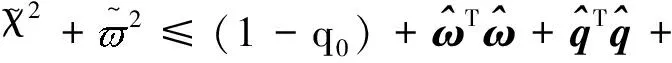

(26)
根据假设4,式(23)可以写为

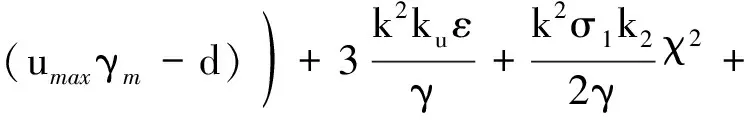

(27)
式中:=()。
引入新的变量0<<1,式(27)可进一步写为:
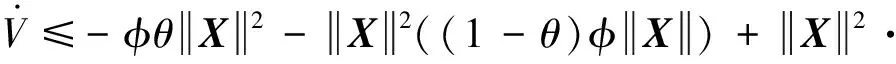


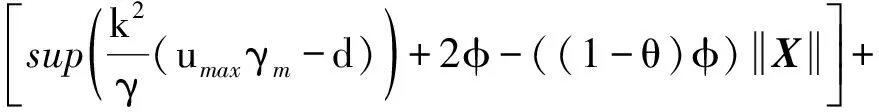
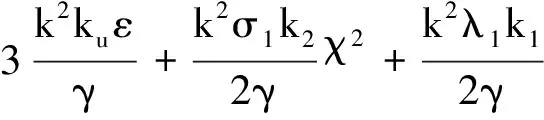
(28)


(29)
式(28)可以写为
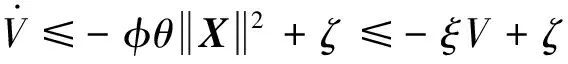
(30)
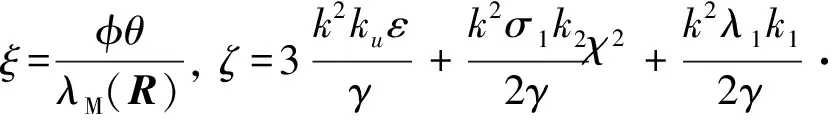
将式(30)两边积分可得
0≤()≤((0)-)e-+
(31)
因此,根据式(13)和式(31),可以得到

(32)
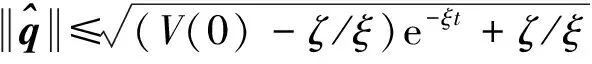
(33)

根据以上得到的结论,可以得到姿态增益也是有一致界的。根据式(4)和式(5),并且结合假设2可以得到

(34)
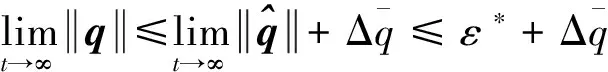
(35)
根据式(34)和式(35)可得:实际的角速度和实际的姿态也是一致有界的,他们会收敛到平衡位置的较小邻域内。证毕。
根据式(12)和(22),所提出的控制器不依赖于故障的准确信息,仅使用估计故障信息的上限和下限。在不存在故障检测与隔离(FDI)的情况下,这些值可用故障信息的极值来代替以获得良好的控制性能,例如=01,=1。

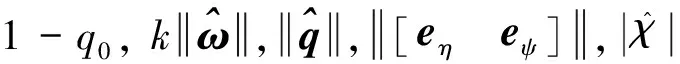
3 数值模拟
在数值仿真中,刚体航天器转动惯量选取为

航天器受到的外部干扰设置为
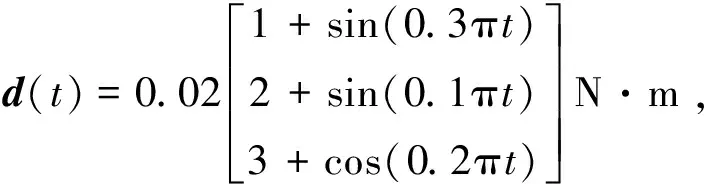
不确定性惯性矩阵Δ=05,假设测量不确定为

执行机构的有效性为
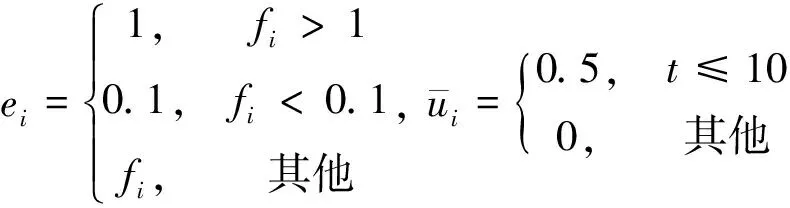
式中:=03+01sin(05+π3),=1, 2, 3。
控制器参数选择=5,=0.01,=01,=10,==0.2,==05,=01,=1,=15,=。
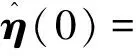
[(0)(0)]=
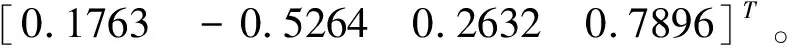
为了验证本文提出控制方法的鲁棒性和有效性,给出两种情形下的仿真结果。
:采用本文设计的控制器式(12),进行数值仿真研究,仿真结果如图3~8所示。

图3 角速度时间历程图Fig.3 Time history of angular velocities

图4 姿态四元数时间历程图Fig.4 Time history of attitude quaternions

图5 估计的晃动位移变量时间历程图Fig.5 Time history of estimated sloshing variables
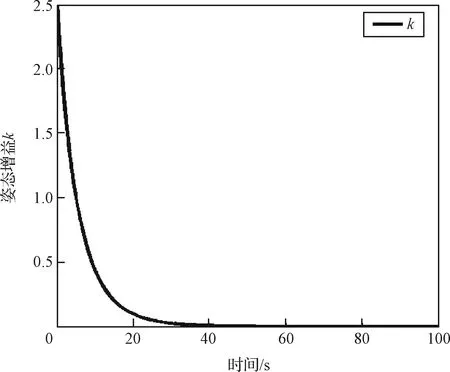
图6 姿态增益时间历程图Fig.6 Time history of attitude gain

图7 参数估计时间历程图Fig.7 Time history of parameter estimation
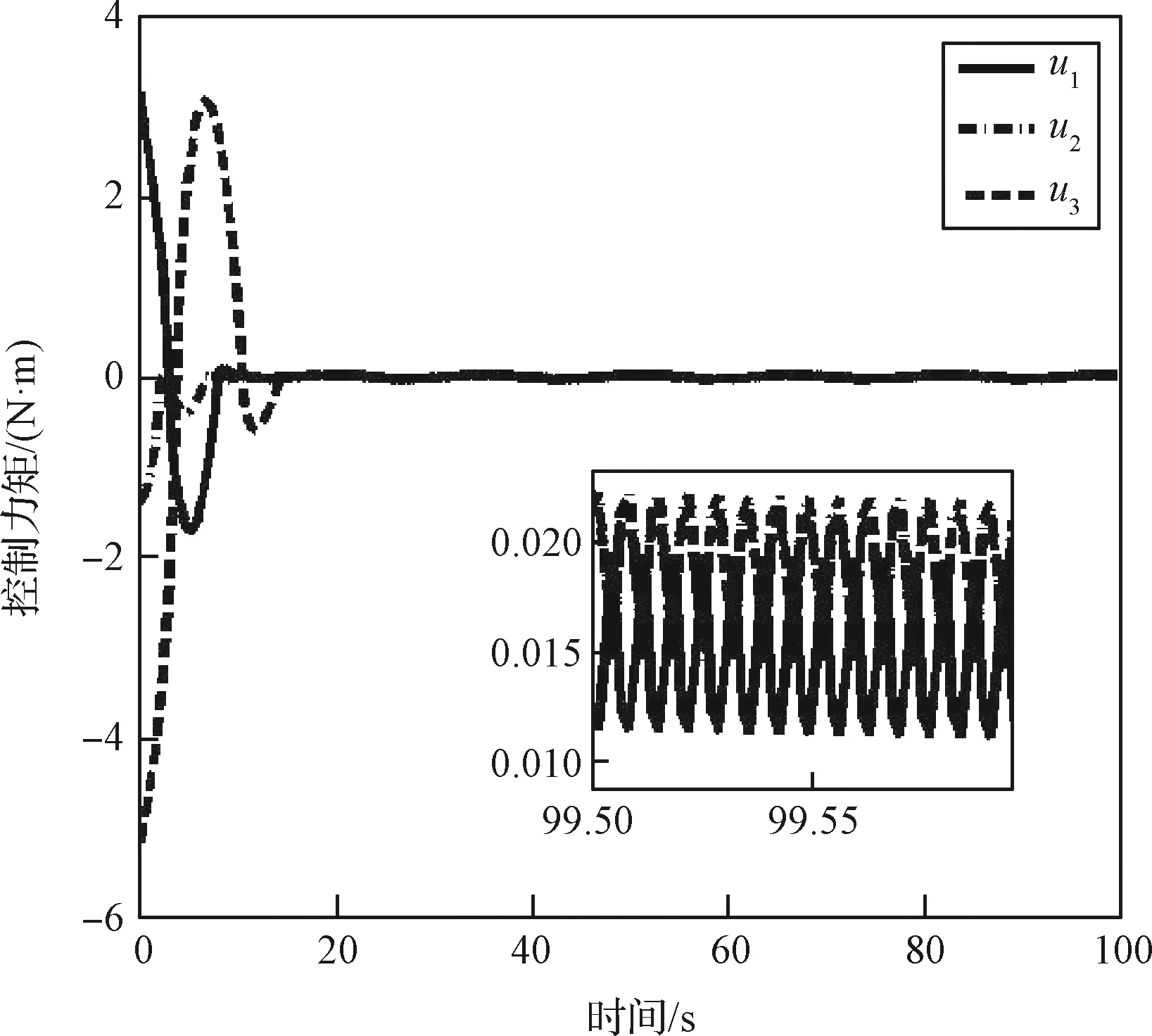
图8 控制力矩时间历程图Fig.8 Time history of control torque
:选择文献[20]中针对刚体航天器设计的鲁棒容错控制器进行对比研究。为了便于控制效果对比,将其设计的控制器在本文充液航天器的控制系统式(7)的环境下进行数值仿真研究。仿真结果图9~11分别给出了航天器姿态角速度,姿态四元数以及控制力矩的响应曲线图。

图9 基于文献[20]控制器的角速度时间历程图Fig.9 Time history of angular velocities by[20]

图10 基于文献[20]控制器的姿态四元数时间历程图Fig.10 Time history of attitude quaternions by[20]
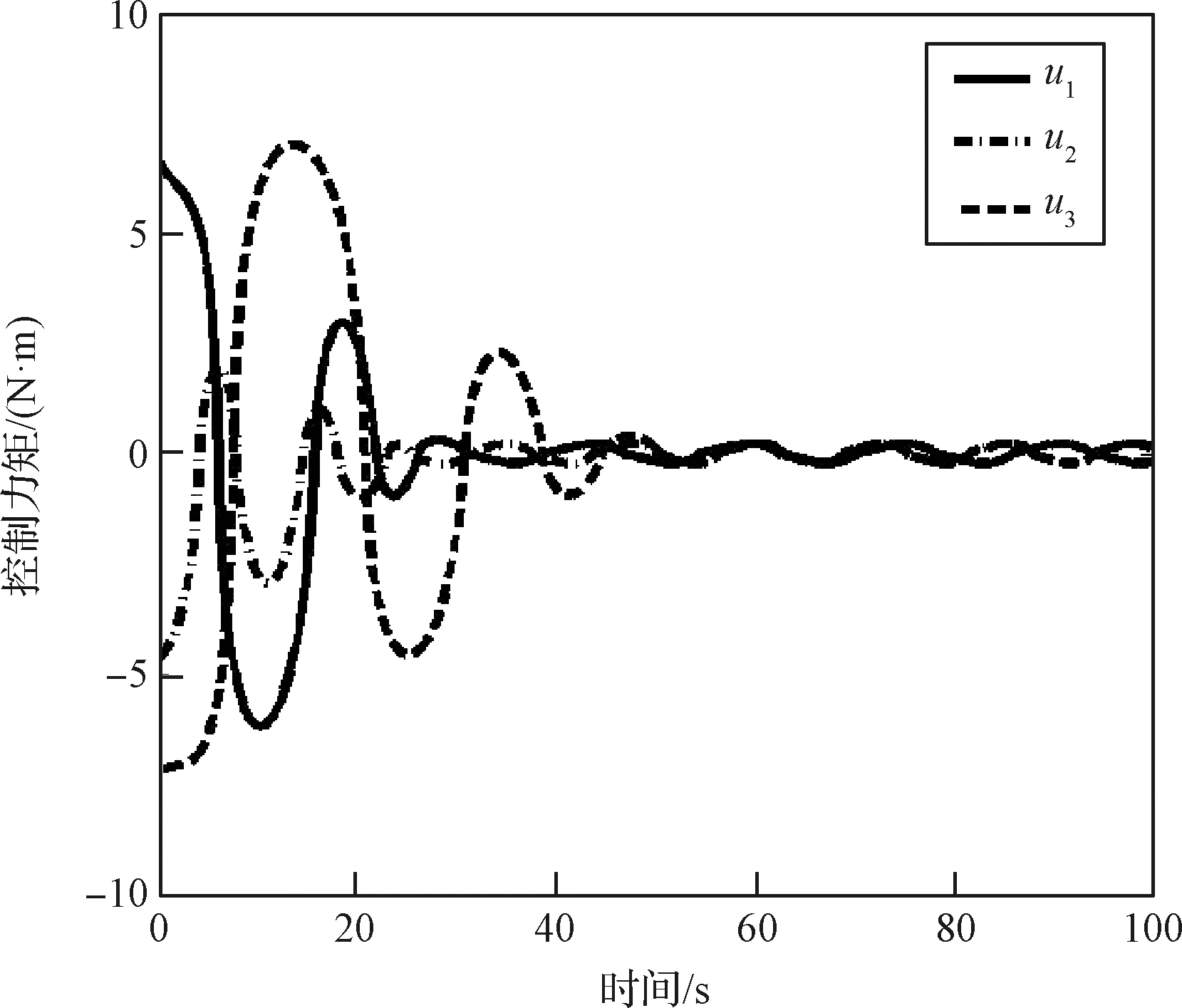
图11 基于文献[20]控制器的控制力矩时间历程图Fig.11 Time history of control torque by[20]
通过以上仿真结果,可以得到以下结论:
1)对比图3和图9中角速度的响应曲线,可以看出在本文控制器式(12)的仿真下,角速度响应需要花费大约20 s的时间收敛到平衡位置,同时在稳态响应阶段的稳态误差精度可以达到||≤1×10rad·s,能够拥有较高的控制精度。在文献[20]设计控制策略仿真下,角速度响应需要花费大约50 s的时间收敛到平衡位,稳态区间的误差精度为||≤5×10rad·s。同时,对比两种控制策略在瞬态响应区间的控制效果,相比较图9而言,可以很明显地看出图3拥有较好的瞬态响应。
2)对比如图4和图10姿态四元数的响应曲线,可以看出在本文设计控制律式(12)的仿真下,姿态四元数需要花费大约20 s的时间收敛到平衡位置,并且在稳态响应区间的稳态误差精度可以达到||≤1×10。在文献[20]的控制策略仿真下,姿态四元数需要花费大约50 s的时间收敛到平稳位置,在稳态响应区间的稳态精度误差可以达到||≤5×10。在对比瞬态响应区间的控制效果,很清楚的看出图4拥有相对较好的瞬态响应。


通过以上分析可以得出,通过比较描述系统状态响应的性能收敛指标,容易得出在相同外部未知干扰、参数不确定,测量不确定和执行器失效的条件下,对比文献[20],本文所提出自适应变结构控制方法能够实现更好的控制性能。
5 结 论
本文以三轴稳定充液航天器的动力学建模和控制策略为研究对象,研究了其姿态控制系统中存在外部未知干扰,参数不确定,测量不确定和未知执行器故障的鲁棒容错控制问题,提出了一种基于变结构控制的自适应鲁棒容错姿态控制方案。
在姿态控制器设计中,将时变变结构控制器结合自适应算法设计了自适应鲁棒容错控制器,提出的控制算法在继承变结构控制策略优点的同时,又能利用自适应算法估计和补偿系统的集总扰动。采用Lyapunov稳定性理论证明了整个容错系统中状态变量的一致最终有界稳定性。最后与现有的变结构控制方法进行了仿真对比研究,仿真结果表明,本文设计的控制器可以实现充液航天器控制系统的快速收敛性能和鲁棒容错能力。

