一种多策略改进的麻雀搜索算法

张 琳，汪廷华，周慧颖

赣南师范大学 数学与计算机科学学院，江西 赣州 341000

群智能算法是受自然界生物群体社会行为模式、进化机制、物理现象的启发而开发的随机搜索算法，具有简单易实现、灵活性、鲁棒性强、自组织性等特点，在图像处理、模式识别、数据挖掘、系统控制等领域被广泛应用。近年来，国内外学者相继提出各种群智能优化算法，如：蚁群算法（ant colony optimization，ACO）[1]、粒子群算法（particle swarm optimization algorithm，PSO）[2]、果蝇优化算法（fruit fly optimization algorithm，FOA）[3]、灰狼优化算法（grey wolf optimizer，GWO）[4]、鲸鱼优化算法（whale optimization algorithm，WOA）[5]、哈里斯鹰优化算法（Harris hawks optimization，HHO）[6]、麻雀搜索算法（sparrow search algorithm，SSA）[7]等。其中麻雀搜索算法是由Xue和Shen于2020年提出的一种新型群智能优化算法，源于对麻雀种群捕食行为和反捕食行为的研究。SSA有全局寻优、可调节参数少、结构清晰等优点，被广泛应用于各种实际工程优化问题且均有很好的实际效果，例如图像分割[8-9]、航迹规划[10-11]、车间调度[12]、发电功率预测[13]等。

然而，SSA在求解复杂优化问题时也存在对初始值敏感，迭代后期种群趋同性严重，难以跳出局部最优值的问题，限制了算法的寻优性能。针对这些缺点，诸多学者对其进行了改进研究。Chen等人[14]通过采用Tent混沌初始化麻雀种群位置，并引入levy飞行和随机游走策略有效改善了算法的收敛速度和探索能力。文献[15]在SSA中对麻雀种群位置进行k-means聚类分化，减小随机性对初始种群的干扰，对加入者和最优个体位置更新引入正余弦搜索策略、自适应局部策略进行优化，提升算法的寻优效率和收敛速度。文献[16]对最优解引入柯西变异和反向学习策略提高算法局部空间最优值的逃逸能力。文献[17]在SSA种群初始化过程中引入精英混沌反向学习机制提升初始种群质量，并结合鸡群算法的随机跟随策略优化加入者位置更新增强算法的搜索性能，借助柯西高斯变异策略保证了种群多样性和种群抗停滞能力，避免算法过早收敛。段玉先等[18]利用Sobol序列映射生成初始种群位置，并引入非线性惯性权重和纵横交叉策略协调算法的局部搜索能力和全局开发能力，降低算法陷入局部最优的可能。文献[19]采用ICMIC混沌初始化种群，增加种群的多样性和质量，在发现者搜索机制中融入螺旋探索策略有效增强算法的全局探索能力，借助精英差分和随机反向的混合变异机制，避免因迭代后期种群个体的快速同化导致算法早熟收敛。上述改进策略虽然对SSA的寻优性能有所提升，但寻优后期搜索能力不足和易早熟收敛的问题依然存在。

因此，本文提出一种多策略改进的麻雀搜索算法（multi-strategy improved sparrow search algorithm，MISSA）。根据以下策略对SSA算法进行改进：首先在麻雀种群初始化过程中引入立方序列映射和反向学习机制，提升初始种群的质量和遍历性，实现对搜索空间更全面彻底的搜索；其次，借鉴粒子群算法的学习策略更新发现者的位置，提升种群间的信息交流能力，协调全局勘探和局部开发之间的平衡；最后融合差分进化算法（differential evolution，DE）中的差分变异、交叉操作和反向学习机制对最优解进行变异，增加迭代后期麻雀种群的多样性，使得算法局部最优值的跳出能力有所提升。通过求解8个基准测试函数，并与其他算法进行比较，验证了改进算法的优越性；并将MISSA应用于SVR模型的参数选取之中，在UCI数据集上的实验进一步验证了改进算法的有效性。

1 麻雀搜索算法

在SSA中，麻雀种群可分为负责寻找食物资源并提供整个种群食物位置与方向的发现者和根据发现者提供的食物信息进行捕食行为的加入者，同时在整个种群中随机选取一定比例的麻雀个体对觅食区域进行警戒侦查，一旦察觉到危险，麻雀种群立即做出反捕食行为。在SSA中，种群中适应度较好的麻雀个体被视为发现者，其位置更新如下所示：

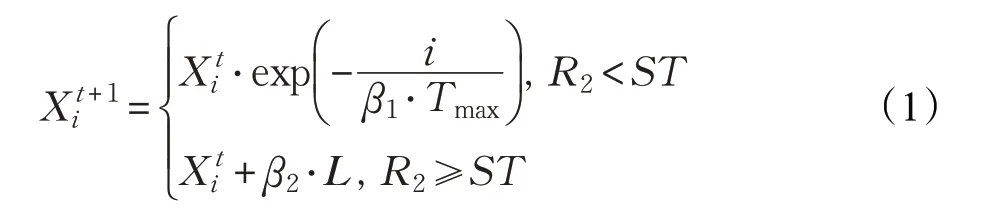
式中，t为当前迭代次数，表示在t代第i只麻雀的位置，Tmax为最大迭代次数，β1∈( )0,1的一个随机数，β2服从正态分布的随机数，L是一个一行多维的全一矩阵，R2∈[0,1]表示警戒值，ST∈[0.5,1]表示安全阈值。当R2＜ST时代表觅食环境安全发现者可广泛搜索，引导种群获取更高的适应度；当R2≥ST时代表可能出现捕食者，需立即向安全区域靠拢。

加入者紧跟发现者进行觅食行为，并可能争夺发现者的食物资源来增加自身捕食率，其位置更新公式为：

在SSA中，侦查者负责监控觅食区域，当意识到危险时会立即发出危险信号，并迅速向安全区域移动或者随机靠近别的麻雀个体来降低被捕食的可能性，其位置更新公式可表示为：

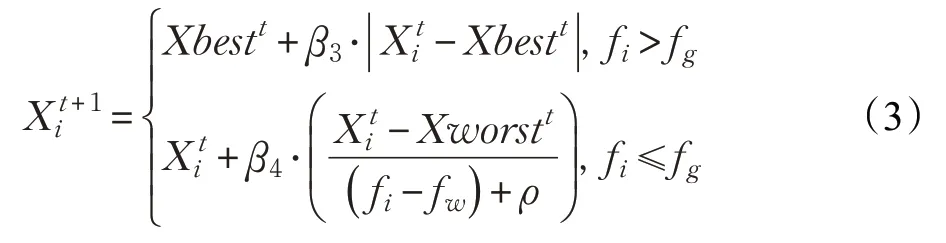
式中，Xbest t为当前全局最优位置，β3是步长控制参数，是一个服从标准正态分布的随机数，β4∈[-1,1]的随机数，ρ的作用是避免分母为0，通常取值为10-50，f i、f g、f w分别为当前个体的适应度、全局最佳适应度及当前全局最差适应度。

2 改进的麻雀搜索算法

2.1 混沌映射和反向学习策略

SSA通过随机生成方式产生初始种群，使得初始种群在搜索空间分布不均匀、遍历性较低，从而导致算法在搜索空间中搜索得不彻底，影响算法的寻优性能和搜索效率。混沌序列映射因具有随机性、遍历性、非重复性、初值敏感性等特点[20]，而被广泛应用于优化搜索问题。通过引入混沌序列映射初始化种群，可以增强初始种群的质量和分布均匀性，有助于算法在搜索空间进行更全面的搜索，实现改善算法的收敛精度和寻优性能的目的。在诸多混沌映射中，立方混沌映射在[0，1]之间均匀分布性能更优，其数学模型为：

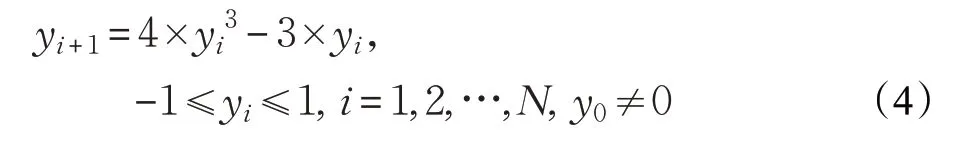
式中，yi为立方序列。若X i∈[lb,ub],lb、ub为搜索空间的上界和下界，将立方序列按式（5）映射到麻雀个体上：

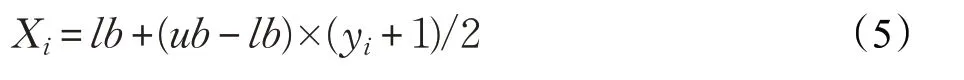
反向学习策略[21]评估问题的可行解及其反向解，选择较优的个体作为算法可行解，扩大搜索空间，进而实现提升初始解的质量，增加算法找到最优解的可能性，降低算法在迭代寻优时的盲目性的目的。个体Xi的反向解OP i可表示为：

式中，k∈(0,1)的随机数。

立方序列映射和反向学习策略初始化种群的具体过程为：

（1）通过式（4）产生立方映射序列，通过式（5）将立方序列映射至麻雀个体上，并计算立方映射种群的适应度值。

（2）通过式（6）寻求立方映射后种群的反向解种群，计算反向解种群的适应度值。

（3）合并立方映射种群和反向解种群后，根据适应度值进行评估，选择适应度值较优的前N个麻雀个体作为初始种群。

2.2 改进发现者的位置更新

在SSA寻优初期，发现者快速收敛于0且向全局最优值的位置聚拢，导致种群多样性骤降，容易出现早熟收敛的状况，从而造成搜索准确性不高的问题。针对这种情况，本文借鉴粒子群算法[2，22]的学习策略，引入全局最优值和个体历史最优值来改进发现者的位置，使得其不仅受全局最优个体位置的影响，还受个体历史最优位置的影响，提升麻雀种群之间的信息交流能力，从而提高算法的搜索速度和寻优精度。改进后的发现者位置更新公式如下：

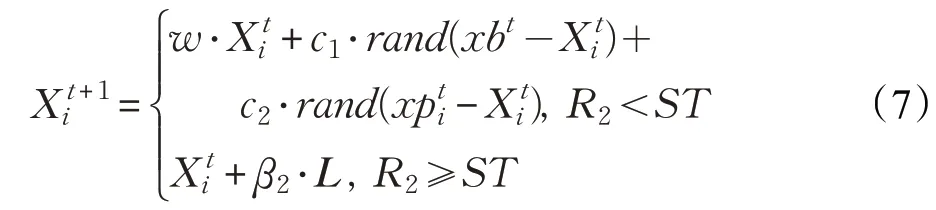
在寻优初期，权重因子大，算法的全局勘探性能强搜索范围广；寻优后期，权重因子快速减小，算法局部开发能力强，有利于快速收敛。

2.3 差分变异策略

在SSA迭代后期，麻雀种群将快速聚集在最优解附近，导致种群趋同性严重，算法停滞不前，进而增大算法陷入局部最优值的概率。为解决此问题，融合差分进化思想[23]至SSA中，通过随机选择两个麻雀个体计算差值与全局最优个体进行变异操作产生新的个体，并对新个体引入反向学习策略，评估比较保留适应度更好的个体，从而改善种群的多样性提升算法局部最优值的逃逸能力，新个体的数学模型可表示为：

式中，X r1、X r2是随机选择的麻雀位置，λ为缩放因子。

3 实验

3.1 基准测试函数上的实验

3.1.1 基准测试函数说明和参数设置

为了验证多策略改进麻雀搜索算法的优化效果，选取了8个基准测试函数对改进算法进行测试检验，具体函数信息如表1所示。

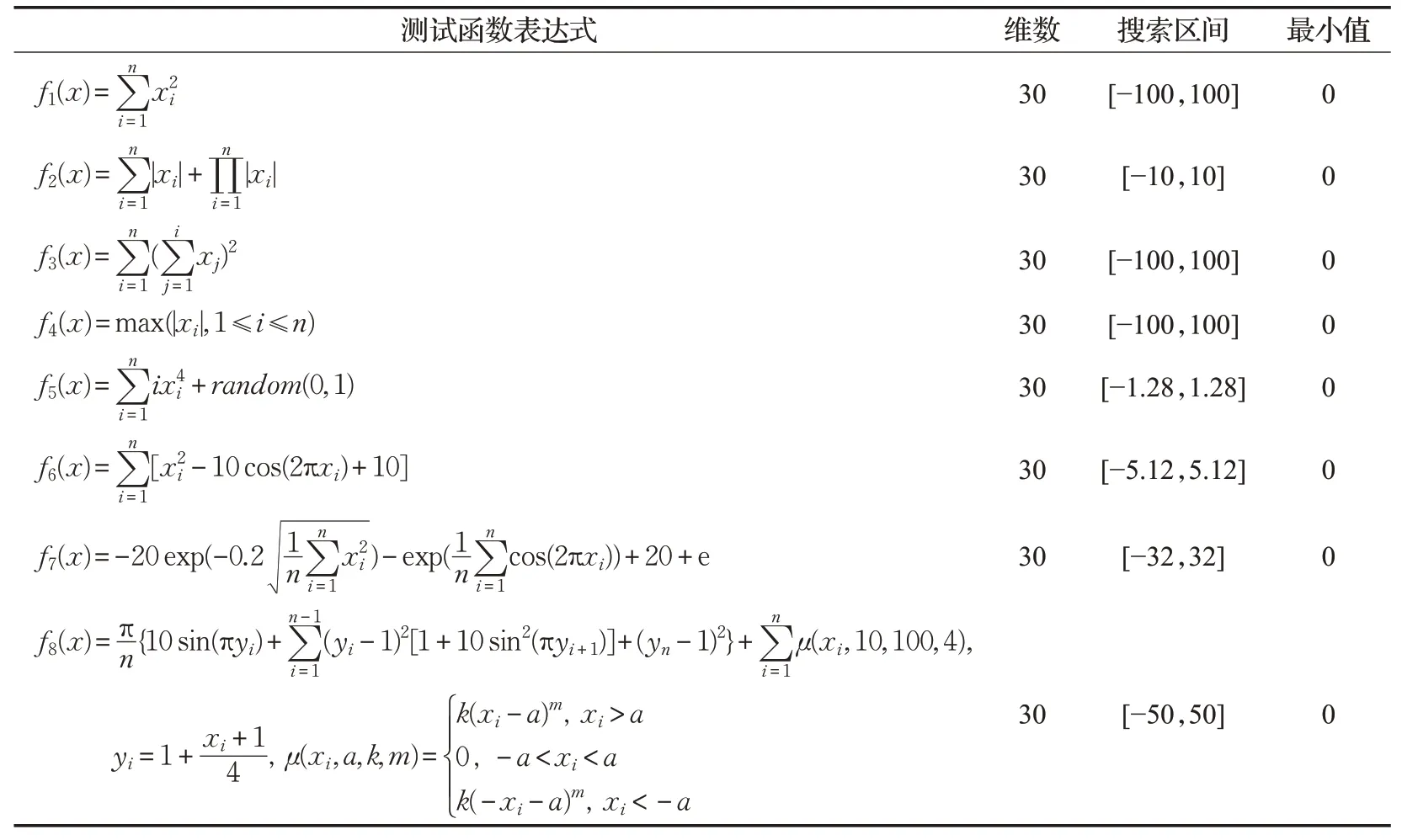
表1 基准测试函数信息Table 1 Benchmark function information

另选取PSO、DE、灰狼优化算法、鲸鱼优化算法、SSA及MISSA进行寻优对比，其中PSO的参数设置为w=0.75,c1=1.5,c2=1.5；DE的参数设置为pcr=0.5,Fmin=0.2,Fmax=0.8；GWO的参数设置为ainitial=2,aend=0；WOA的参数设置为ainitial=2,aend=0,p=0.5,b=1；SSA的参数设置为ST=0.8,PD=0.2,SD=0.2。所有算法的种群规模为30，最大迭代次数为200，每个测试函数独立运行30次来降低算法实验结果的统计误差。表2显示的是30次独立实验中每种算法求解各测试函数的最优解（Best）、最差值（Worst）、平均值（Mean）和标准差（Std）。

3.1.2 实验结果与分析

从表2分析可知：在这8个基准测试函数的寻优实验中，MISSA算法的统计结果明显优于其他5种对比算法。对于单峰函数f1、f2、f3、f4，MISSA算法能够找到其理论最优解，寻优效果远超PSO、DE、GWO、WOA、SSA，对于函数f3、f4，SSA虽也能找到最优值，但最差值、平均值、标准差远远不如MISSA算法；对于单峰函数f5，这几种算法结果表现差别不大，但MISSA算法寻优效果和收敛效率稍微优于其他5种算法。对于多峰函数f6、f7，SSA和MISSA都能稳定地寻找到最优值，说明了该算法本身的优越性；对多峰函数f8，MISSA算法在最优值、平均值和标准差相比于其他算法有所提升。综合分析表明，在寻优过程中MISSA的平均值和标准差均略优于其他算法，表明MISSA算法的寻优精度和鲁棒性明显优于其他算法，说明改进后的麻雀搜索算法能更充分高效地探寻搜索空间，并具备较强的全局寻优能力和局部探索能力。

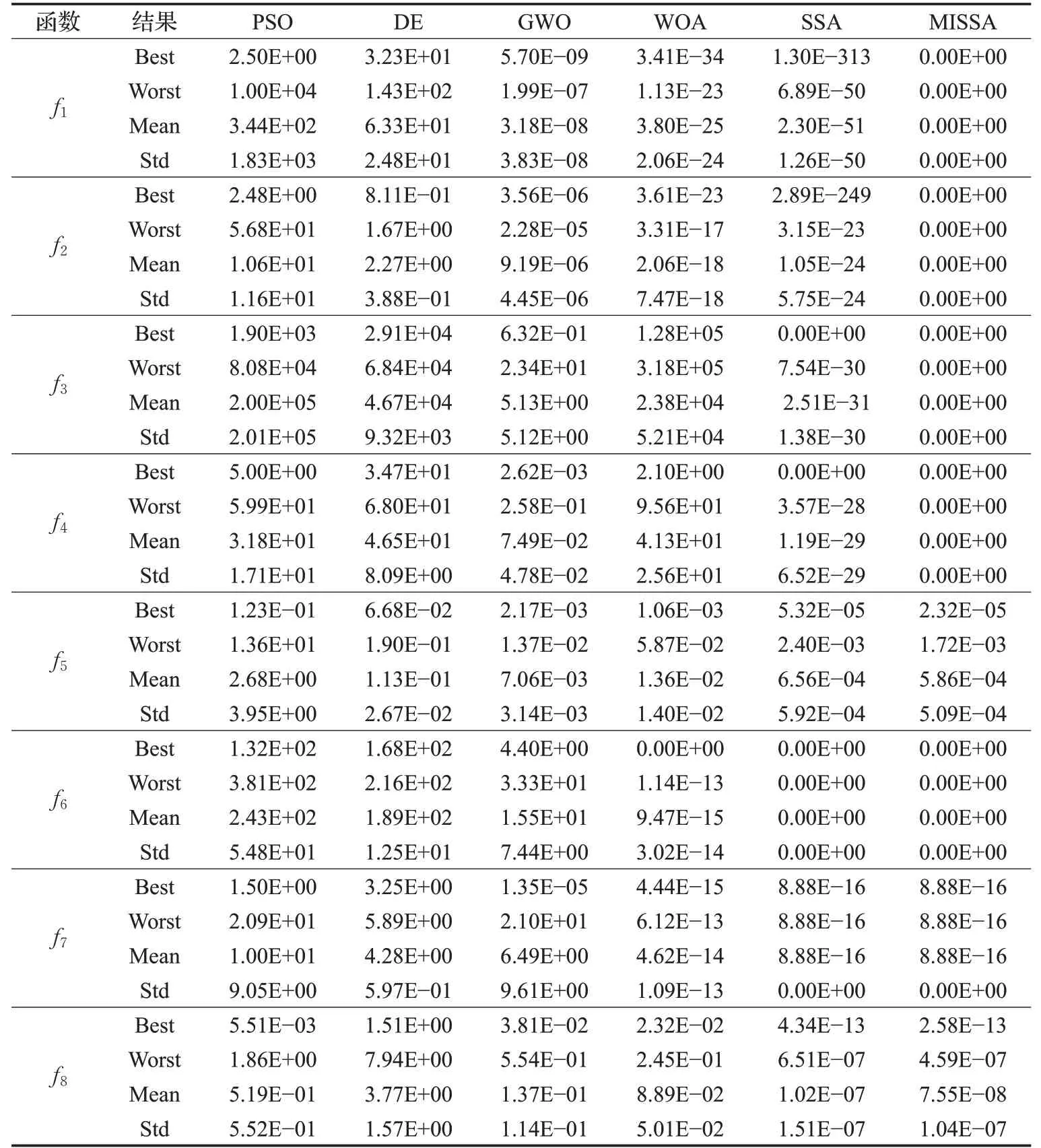
表2 基准测试函数优化结果对比Table 2 Comparison of benchmark function optimization results

为了更好地说明MISSA有着更好的寻优精度以及收敛速度，在8个基准测试函数上进行仿真实验，各算法优化测试函数的收敛曲线对比如图1～图8所示。

从图1至图8可以看出，不论是单峰函数还是多峰函数，在收敛到相同精度的情况下，改进后的MISSA所需迭代次数最少，说明该算法的收敛速度有所提高。在相同的寻优次数，MISSA的求解精度略高于其他算法的求解精度。

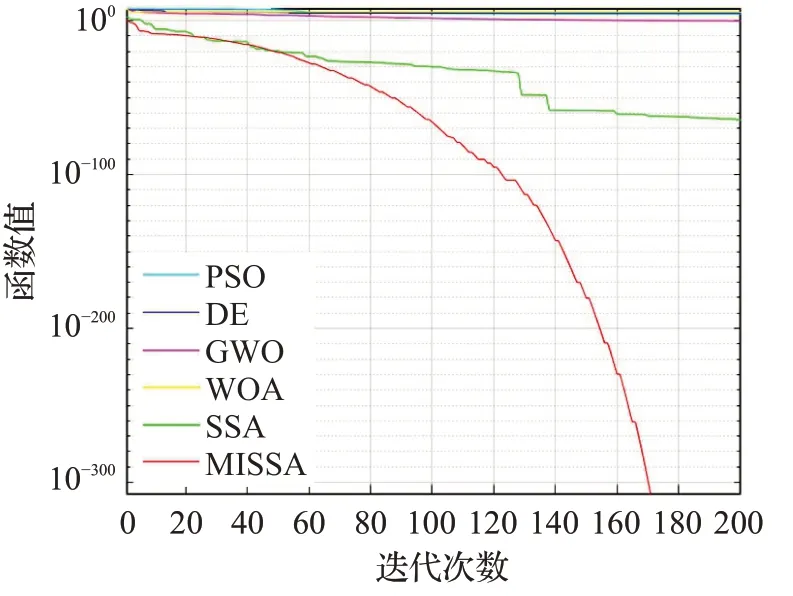
图3 f3函数收敛曲线Fig.3 Convergence curve of f3 function

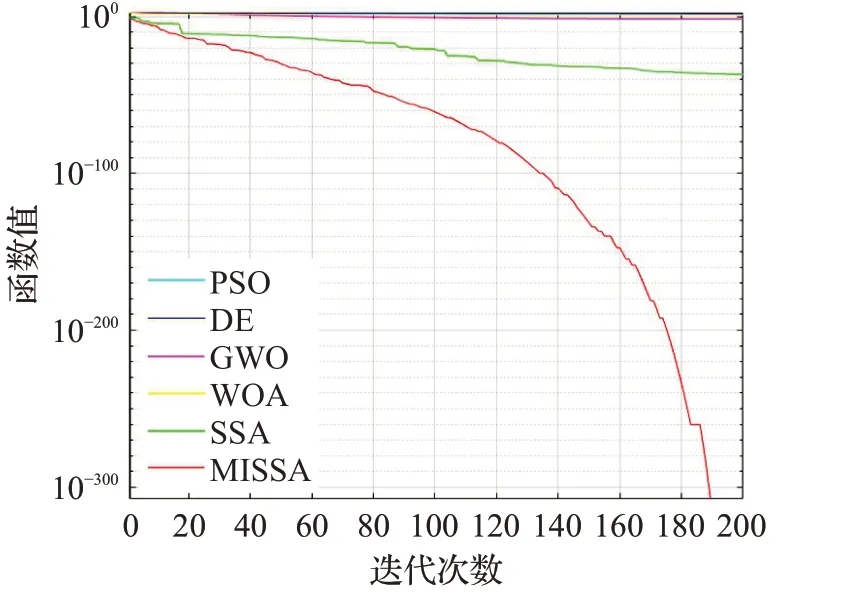
图4 f4函数收敛曲线Fig.4 Convergence curve of f4 function

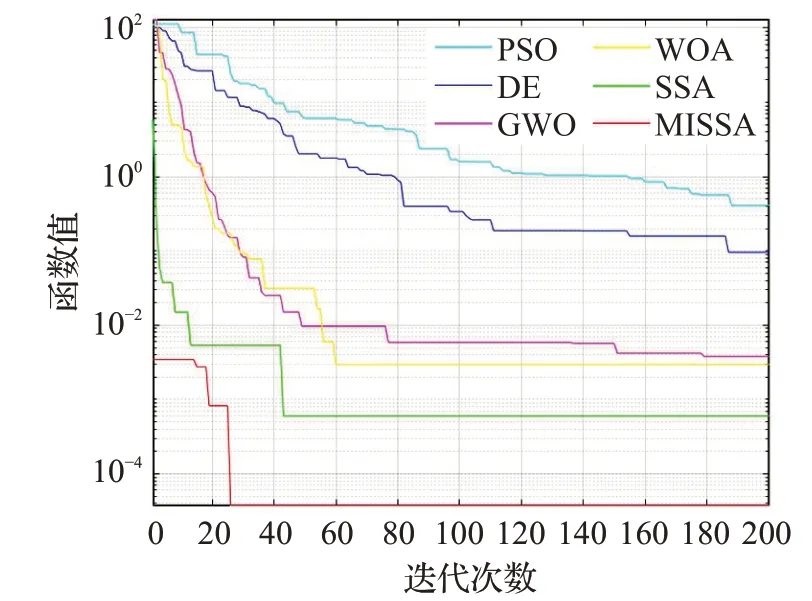
图5 f5函数收敛曲线Fig.5 Convergence curve of f5 function

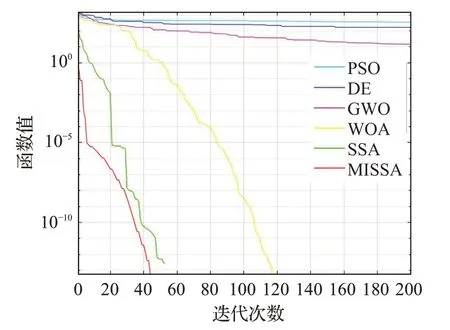
图6 f6函数收敛曲线Fig.6 Convergence curve of f6 function

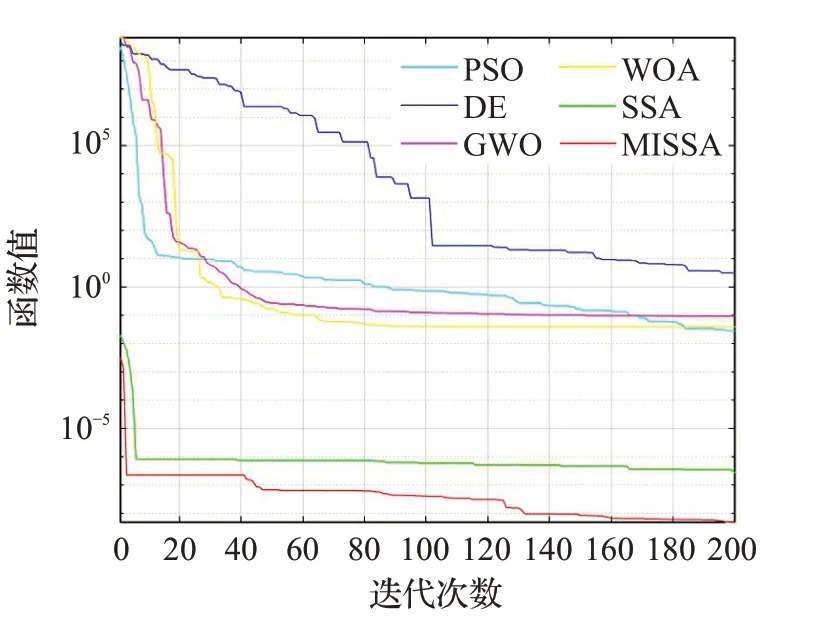
图8 f8函数收敛曲线Fig.8 Convergence curve of f8 function

3.2 SVR模型参数优化对比实验

为进一步验证MISSA的优化性能，将其应用于SVR[24]模型的参数优化选取之中。SVR是建立在统计学习理论上的一种机器学习算法，常用来处理函数拟合和回归预测问题。SVR模型的性能与参数选取紧密相关，参数选择不恰当会降低算法的学习能力和泛化性能[25]。为提高模型性能，本文利用MISSA对SVR中的惩罚系数和核函数中的参数进行优化选择。

3.2.1 MISSA优化SVR参数流程图

利用MISSA对SVR参数进行寻优的流程图如图9所示。首先将数据集进行归一化处理并划分训练集和测试集，然后利用MISSA对SVR模型参数进行优化选择，获得优化模型MISSA-SVR，最后通过优化模型得到预测结果。

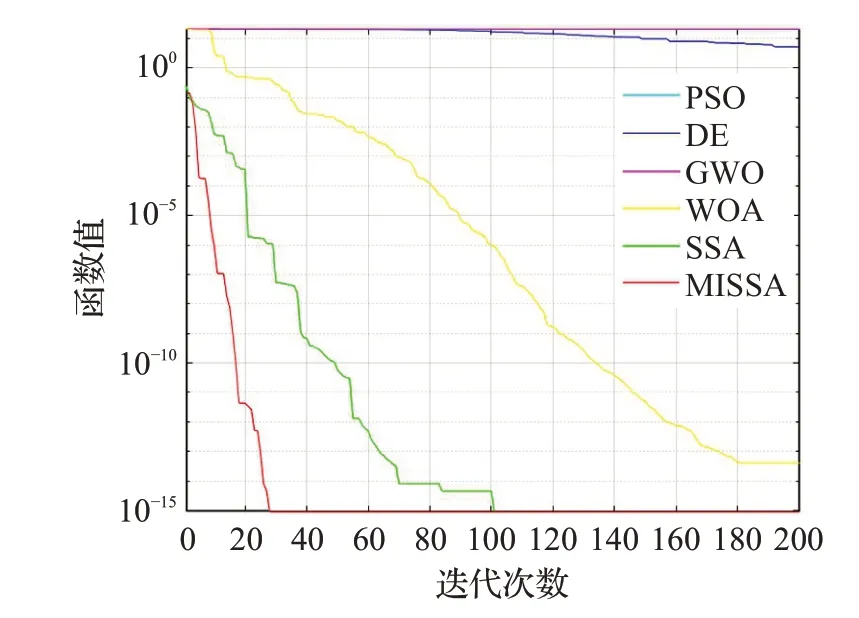
图7 f7函数收敛曲线Fig.7 Convergence curve of f7 function

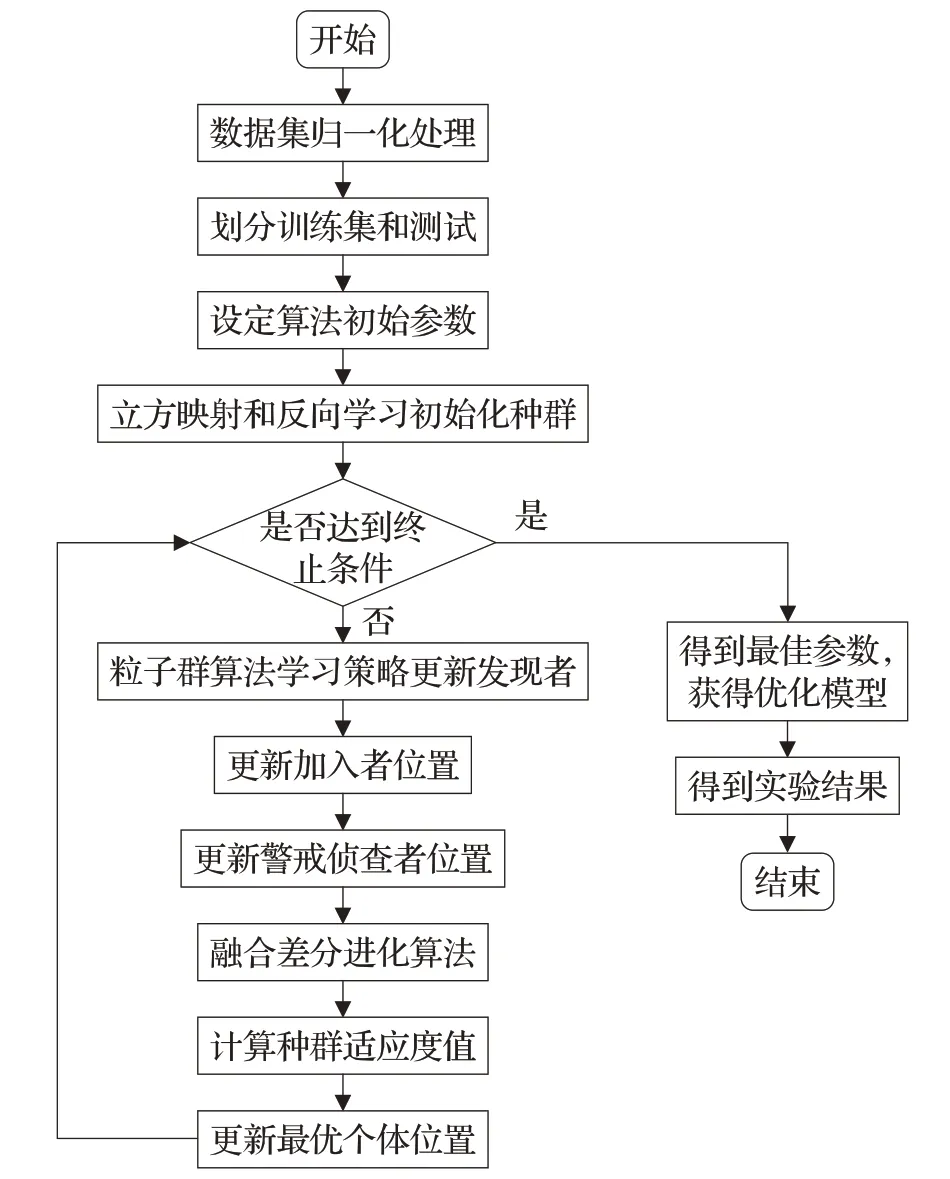
图9 MISSA-SVR参数优化流程图Fig.9 Flow chart of MISSA-SVR parameter optimization

3.2.2 实验数据集与实验设置

从UCI机器学习库[26]中选取了5个数据集来验证MISSA优化SVR模型参数的综合性能，关于数据集的详细信息见表3所示（其中Garments数据集去除包含缺失值的样本后剩余691个数据样本）。

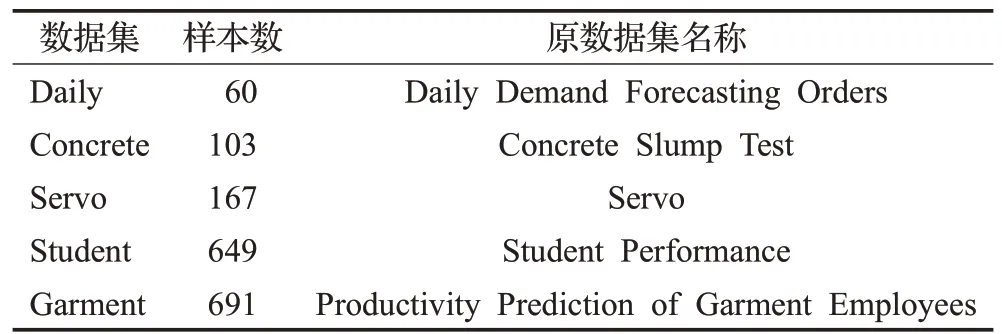
表3 数据集的统计信息Table 3 Statistics for datasets

将数据集去除缺失值后归一化到[0，1]区间，训练集和测试集按照1∶2的比例随机划分，核函数选择径向基核函数，惩罚参数C∈[10-2,25]，核参数γ∈[10-3,24]。为验证改进模型的泛化效果，构建了SVR、PSO-SVR、DE-SVR、SSA-SVR与MISSA-SVR模型进行对比，各模型参数设置如上文所示。通过平均绝对误差（mean absolute error，MAE）、均方根误差（root mean square error，RMSE）、决定系数（R-square，R2）三个评价指标来评估各模型的预测精度，评价指标的计算公式如下所示：

3.2.3 实验结果与分析

表4显示的是5种算法在5组数据集上优化SVR算法参数的实验结果，其中粗体数字表示这些方法在每个数据集上的最佳性能。

通过表4可知，本文提出的MISSA-SVR模型在预测性能上有一定的提升，相比较于其他算法优化参数的SVR模型具有更高的预测精度。从表4分析可得，MISSA-SVR模型在选定的5种数据集上的RMSE、R2取得的效果最好，在4种数据集上MAE表现最好，其中在Servo数据集上，SVR模型达到了和MISSA-SVR模型一样的MAE评价指标，但MISSA-SVR的RMSE和R2略微优于SVR模型。综合分析表明MISSA-SVR模型在相同条件下，泛化性能有明显的提升。

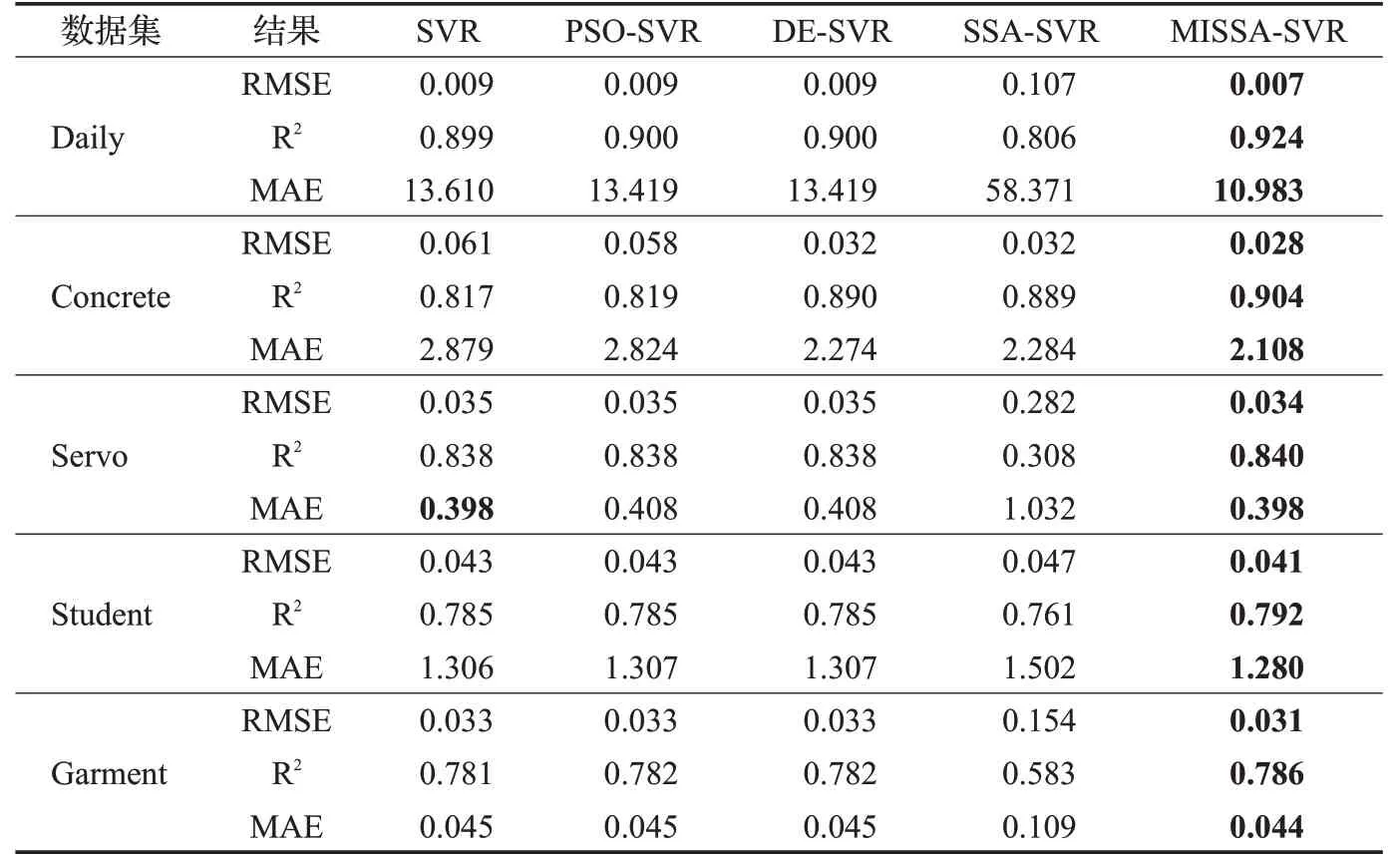
表4 各算法优化SVR的实验结果Table 4 Experimental results of optimizing SVR for each algorithm

4 结语

针对SSA在求解优化问题时存在的缺点，本文提出了一种多策略改进的麻雀搜索算法。通过立方序列映射和反向学习策略改进SSA初始种群的质量，借鉴粒子群算法的学习策略提高种群间信息交流能力，利用差分变异操作和反向学习机制增加SSA迭代后期的种群多样性，提高算法陷入局部最优值的逃逸能力，从而提升算法的寻优精度和收敛效率。通过对8个基准测试函数的寻优实验，实验结果表明MISSA具有更好的求解精度、收敛速度和鲁棒性，相较于麻雀搜索算法综合性能有明显的提升，验证了MISSA算法的改进效果。采用MISSA算法对SVR模型中核参数和惩罚参数进行优化选择，进而构建了MISSA-SVR预测模型。通过对5个UCI数据集进行预测分析，结果表明改进模型具有较好的预测精度，进一步验证了改进算法的有效性和应用可行性。在未来研究中，可将MISSA用于解决更加复杂的实际问题。