空频域图像增强方法研究综述

郭永坤，朱彦陈，刘莉萍，黄 强

1.江西中医药大学 计算机学院，南昌 330004

2.江西中医药大学 网络中心，南昌 330004

在人们的生活、生产中，数字图像的处理已无处不在，例如医疗、军事、工业、民用等各个领域图像都被广泛应用。数字图像处理的历史可追溯至二十世纪二十年代。最早应用之一是在报纸业。那么，什么是图像处理。图像处理（image processing）是指用计算机的手段对图像进行科学分析，以达到所需结果的技术，又称影像处理。图像处理一般指数字图像处理。数字图像是指用摄像机、扫描仪等一系列辅助设备经过拍摄得到的二维数组，该数组的元素称为像素，其值称为灰度值。然而，有些数字图像往往存在着模糊区，给图像的识别带来了诸多不便，为了更加准确地识别图像，图像增强技术应运而生。图像增强技术是一种基本的图像预处理手段，它改善原始图像的视觉效果或某种程度的滤噪，以便于后续的图像处理，其最终目的是为了提高图像质量，加强图像判读和识别效果。最早应用在医学图像处理领域的图像增强方法大多为简单的空间域图像增强方法，对模糊的图像进行数字增强后再进行图像识别。由于起初对于医学图像的处理要求简单，一般采用一些空间域的手段即可，但是随着医学的发展，对于图像处理的要求更加严谨，陆续出现了更多的基于空间域、频域的图像增强方法，增强的效果也因此得到了不同程度的改善。详细的图像增强方法分类框架图如图1所示。随着图像处理领域研究的不断深入，传统的图像增强方法已无法满足要求。为此，本文对图像增强方法进行综述分析，将其分为空域图像增强方法和频域图像增强方法，并分别对这些方法的性能、效果进行对比，以便为进一步研究图像增强算法或者改进图像增强方法提供参考与借鉴。

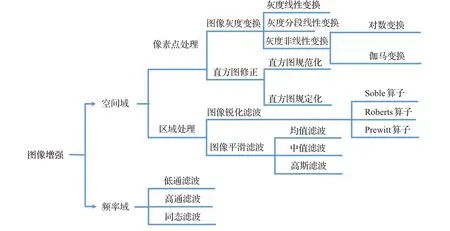
图1 图像增强方法分类框架图Fig.1 Classification framework of image enhancement method

1 空域图像增强方法

空域是指组成图像的像素的集合，空域的图像增强直接作用于图像中像素灰度值，基本上是以灰度映射为基础进行运算处理的。基于空域的图像增强方法[1]主要有直方图修正[2-3]、灰度变换[4-5]和空域滤波[6-9]等方法。

1.1 直方图修正图像增强算法

图像直方图是图像处理中一种十分重要的图像分析工具，它反映的是一幅图像中各灰度级像素出现的频率与灰度级间的关系。其目的是，增大反差，突出图像细节，从而达到图像增强。直方图修正可分为直方图均衡化和直方图规定化两种方式，直方图均衡化HE[10]又称直方图平坦化，主要用于增强动态范围偏小的图像的对比度。直方图规定化HS[11]主要是依据目标图像均衡化，可看作是直方图均衡化的改进。如图2所示，直方图均衡化后图像整体对比度更强，灰度分布较均匀（以藏药臭蚤草植物图像为例），如图3所示，直方图规范化后图像整体目标性更强（以川百合植物图像为例）。直方图修正算法对灰度级相对集中、背景和前景都太亮或者太暗的图像处理效果较好，但对含有噪声的图像效果不明显，并且均衡化处理后可能会造成灰度级减少，易产生一些伪影，对比度过分增强。为此，纪平等人[12]提出一种改进自适应直方图均衡化算法，先采用加权平均值，再用滤波器处理噪声，消除噪声的影响，从而提高了图像增强的效果，但存在着两个明显的缺陷：（1）计算复杂度增加了，造成了大量的空间浪费现象。（2）算法运行在很大程度上存在着人工的干扰。Chang等人[13]提出了各种针对特定问题的基于HE的方法，解决增强图像中的伪影问题。但针对特定问题时，可能会造成过拟合现象。Zahedi等人[14]提出了一种新的颜色直方图均衡化方法，该方法基于一维直方图定义了一个新的三维累积分布函数，以解决产生的伪影问题。但该方法同样受到颜色通道之间相关性的影响较大。Ling等人[15]提出了一种用于暗图像增强的自适应扩展分段直方图均衡算法（AEPHE），以解决过度增强或增强不足问题。但如果原始图像的灰度空间很小时，会造成扩展分段不合理，致使图像增强效果降低。

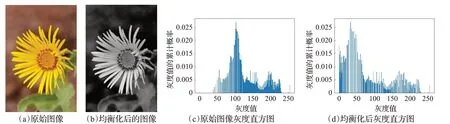
图2 直方图均衡化Fig.2 Histogram equalization

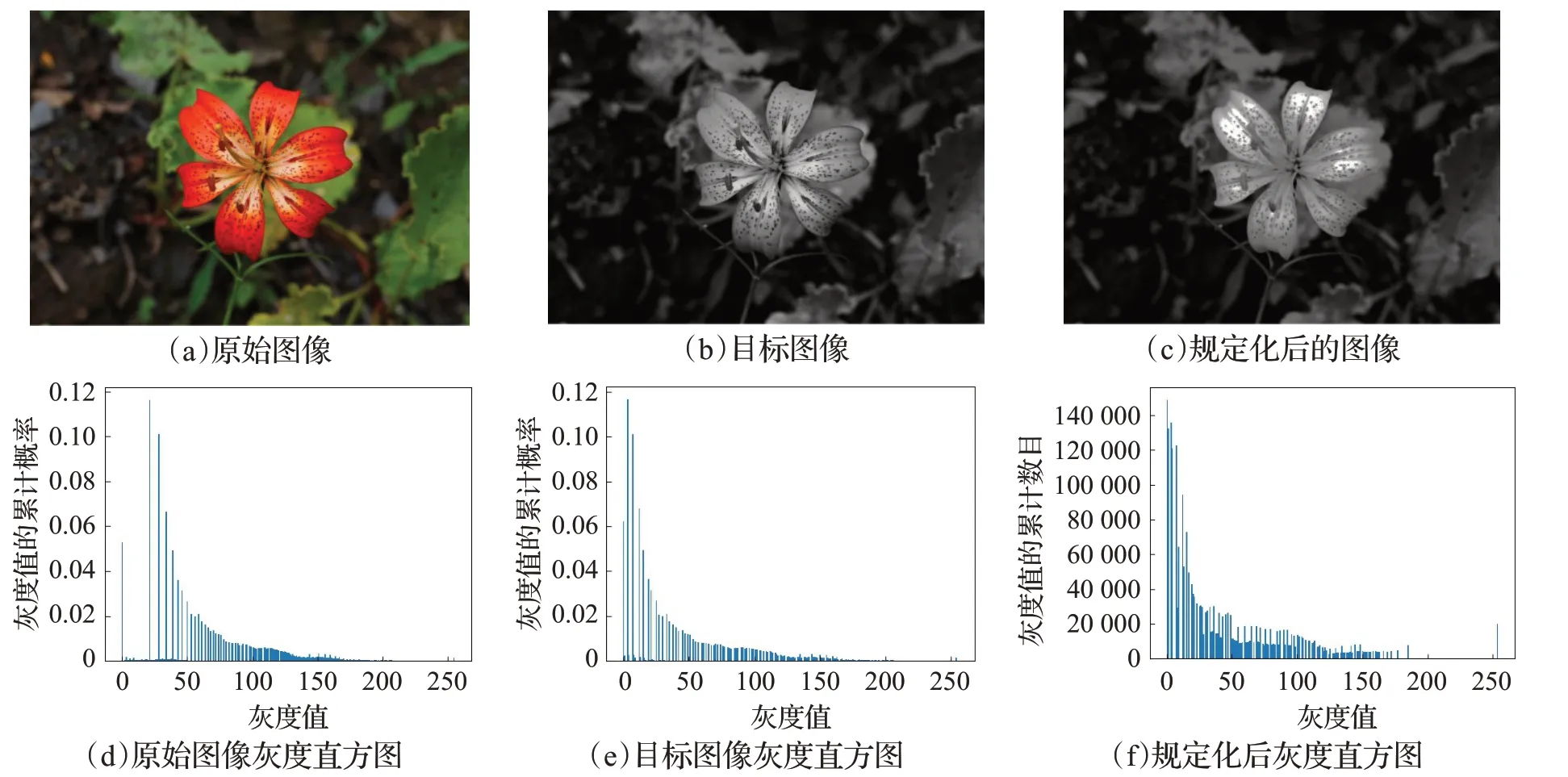
图3 直方图规定化Fig.3 Histogram specification

1.2 灰度变换图像增强算法

灰度变换[16]可使图像动态范围限制缩小，图像对比度增大，图像清晰度增高，以改善图像视觉效果。灰度变换一般可以分为线性、分段线性和非线性变换三类。线性变换[17]是通过建立灰度映射来调整资源图像的灰度，对图像的灰度做线性扩张或压缩，从而达到图像增强的目的。其主要包括反色变换、上移变换和对比度变换等等。分段线性变换[18]是指在一些明亮段拉伸，在另一些明亮段压缩，以调节图像的对比度，其目的是为了突出某些有用的信息。其主要包括灰度拉伸、灰度窗口变换等。非线性变换[19]是通过压缩不关注部分，只对关注部分进行处理。其主要包括对数变换[20]、幂次变换[21]、分段函数变换[22]等等。为了更加明显区分三类算法的不同，分别选用其代表算法线性变换-反色变换LIT、分段线性变换-对比度拉伸PL-TCS和非线性变换-伽马变换NL-TGT展示三类变换的效果，如图4所示（以藏药刺花莲子草植物图像为例）。相比于直方图，灰度变换的方法算法较为简单，映射函数选择较为灵活，得到了广泛应用，如张志伟等人[23]利用一种基于幂律灰度变换的改进型分段幂律曲线模型，对水下焊缝图像处理，以有效提高焊缝边缘信息的对比度。但在低灰度和高灰度区域存在像素点较少的图像，灰度拉伸效果有很大的影响；并且存在灰度值孤立点，会导致存在分段点有一边拉伸效果不明显，图像整体偏暗或者偏亮的现象。华尉然等人[24]采用伽马灰度变换对非暗区域处理，使得图像亮度、清晰度低图像能清晰表现出夜间场景中事物轮廓，从而增加图像增强效果。但是对于界定上下限灰度的临界值不易选取，对增强图像效果的影响很大。Ding等人[25]采用Radon变换消除了噪声的影响，从而增强成像质量差的图像效果。但是也大大增加了内存的消耗，增加了软硬件的容量风险。

图4 灰度变换Fig.4 Gray scale transformation

1.3 空域滤波图像增强算法

空域滤波可分为平滑滤波和锐化滤波，其中平滑滤波有均值滤波[26]、中值滤波[27]和高斯滤波[28]；锐化滤波有Soble[29]算子、Roberts[30]算子和Prewitt[31]算子滤波。平滑滤波是低频增强的空间域滤波技术，其本质上是一种低通滤波手段，它的目的是模糊图像或者降低噪音，其滤波效果如图5所示。锐化滤波的主要目的是为了突出灰度的过渡部分并补偿缺失的轮廓，增强图像的边缘及灰度跳变的部分，使图像变得清晰。与平滑滤波不同的是，锐化滤波器是使用邻域的微分作为算子，增大邻域间像素的差值，使图像的突变部分更加明显，滤波效果如图6所示（以藏药甘青青兰植物图像为例）。两者效果相反，互为补充，从原始图像中减去平滑滤波器的结果能得到锐化滤波器的效果，而从原始图像中减去锐化滤波器的结果则可以得到平滑滤波器的效果。现阶段已有大量平滑滤波和锐化滤波相关研究文献，如王云艳等人[32]利用Sobel算子提取出边缘掩膜，再利用平滑滤波处理提取细节，两者结合可得到效果更好的边缘细节增强图像。但存在图像边缘信息过分增亮的现象。对于平滑过程中产生的细节模糊问题，冯策等人[33]提出了自适应的非锐化掩模深度图像增强算法，只提取出不含噪声的高频部分，克服了经典非锐化掩模算法放大高频噪声的缺点。但该方法在修复较大缺失过程中比较耗时，滤波窗口的尺寸不满足实时性的需求。为解决图像亮度、对比度低的问题，田文利[34]提出了基于滤波与锐化的遥感图像增强算法，建立了基于Sobel与Laplacian的图像锐化增强算子，以增强图像对比度。但是没有考虑到在两次锐化中极易丢失一些信息，可能会导致最后的增强图像信息不完整。

图5 平滑滤波效果图Fig.5 Smoothing filtering effect

图6 锐化滤波效果图Fig.6 Effect of sharpening filtering

2 频域图像增强算法

频域增强[35-39]是利用图像变换方法将原来的图像空间中的图像以某种形式转换到其他空间中，然后利用该空间的特有性质进行图像处理，最后再转换回原来的图像空间中，从而得到处理后图像的过程。频域处理法的基础是卷积定理，它采用傅里叶变换的方法实现对图像的增强处理。在频域空间，图像的信息表现为不同频率分量的组合，如果能让某个范围内的分量或某些频率的分量受到抑制而让其他分量不受影响，使得输出图像的频率分布有规律地变化，以达到增强图像的目的。常用的频域增强方法有低通/高通滤波和同态滤波。

2.1 低通/高通滤波图像增强算法

低通滤波[40]是一种过滤方式，规则为低频信号能正常通过，而超过设定临界值的高频信号则被阻隔、减弱。常用的低通滤波有理想低通滤波、巴特沃斯低通滤波和高斯低通滤波，其滤波效果如图7所示。与低通滤波正好相反，高通滤波通高频抑低频。能检测噪声的急促变化，证实图像的边缘信息，常用的高通滤波有理想高通滤波、巴特沃斯高通滤波和高斯高通滤波，其滤波效果如图8所示。低通/高通滤波常用于指纹识别、人脸识别、医学影像、图像模糊、信号处理等领域，如Yang等人[41]提出了一种新颖的指纹图像增强滤波器设计方法，即改进的Gabor滤波器（MGF），用于指纹识别，解决了伪影问题，但也很可能丢失一些重要信息。Mohammad等人[42]开发了一种新算法，用于在不同光照条件下进行人脸识别，采用低通和高通滤波采集面部图像特征再进行分类识别，但对于什么条件下采用低通和高通滤波采集特征，没有精准的界限。Xia等人[43]提出了一种图像增强与自适应组合低通滤波和模糊增强方法对图像增强和噪声过滤，以提高效果和适应性，但大大增加了算法的复杂度，运行时间较长。Deng等人[44]针对毫米波图像被重模糊和噪声的影响，提出了一种改进的频率空间非线性外推方法，以提高毫米波图像的质量和降低噪声，但非线性滤波器设计较复杂，且易受参数的影响。Liang等人[45]针对偏振去雾方法在不同的成像条件下处理模糊图像不够稳健的问题，提出了一种基于低通滤波的广义极化除雾方法，增强了在不同的雾霾天气和不同密度的散射水下环境中的有效性和鲁棒性，但是没有考虑偏置参数的影响。以上研究大部分都是针对某一缺点而做的改进，但很少考虑到其他的方面，比如文献[41]减少了伪影但也丢失了一些信息，其他研究大都如此，没有综合考虑各因素之间的相关性。

图7 低通滤波效果图Fig.7 Effect diagram of low-pass filtering

图8 高通滤波效果图Fig.8 High pass filtering effect

2.2 同态滤波图像增强算法

同态滤波[46-47]简称为HF算法，是一种在频域中进行的图像对比度增强和压缩图像亮度范围的特殊方法。其能够减少低频并且增加高频，从而能减少光照变化并锐化边缘细节。同态滤波的特点是压缩灰度范围，同时增强对比度，其滤波效果如图9所示。为了更好地解决对比度低和颜色偏差问题，Yu等人[48]提出了一种基于彩色线模型和同态滤波的水下图像增强方法。该方法在定量分析、定性分析、色彩准确度分析、合成水下图像恢复等四个方面均优于当前最先进的方法，尽管如此，但是也大大增加了计算的复杂度，常规的计算方式已经不能满足它的需要，最好使用并行运算的方式。为了解决磁共振MR图像通常存在椒盐噪声以及对比度低的问题，黄雪冰等人[49]提出了自适应加权重复值滤波算法，通过在空域和频域针对不同侧重点分步进行滤波，去除椒盐噪声，提高对比度，增强MR图像。但是该方法有效度不高，同态滤波参数的设置也需要进一步测试和调整。为了解决低照度图像问题，Zhang等人[50]提出了一种图像颜色增强方法来提高图像的亮度和质量，采用局部空间同态滤波提高亮度，梯度域方差来抑制噪声，最终达到增强图像的效果。但没有考虑到对比度和信息丢失的问题，可能会造成图像的视觉效果并不清晰。

图9 同态滤波效果图Fig.9 Homomorphic filtering effect

3 图像增强算法评价与对比

3.1 图像增强效果主观评价

本文编程实现了上述两大类图像增强算法，包括直方图均衡化算法、直方图规定化算法、线性变换、分段线性变换、非线性变换、均值滤波、中值滤波、高斯滤波、Soble算子、Roberts算子、Prewitt算子、低通滤波、高通滤波和同态滤波等17种图像增强算法，采用同一图像进行测试，增强效果如图10所示。

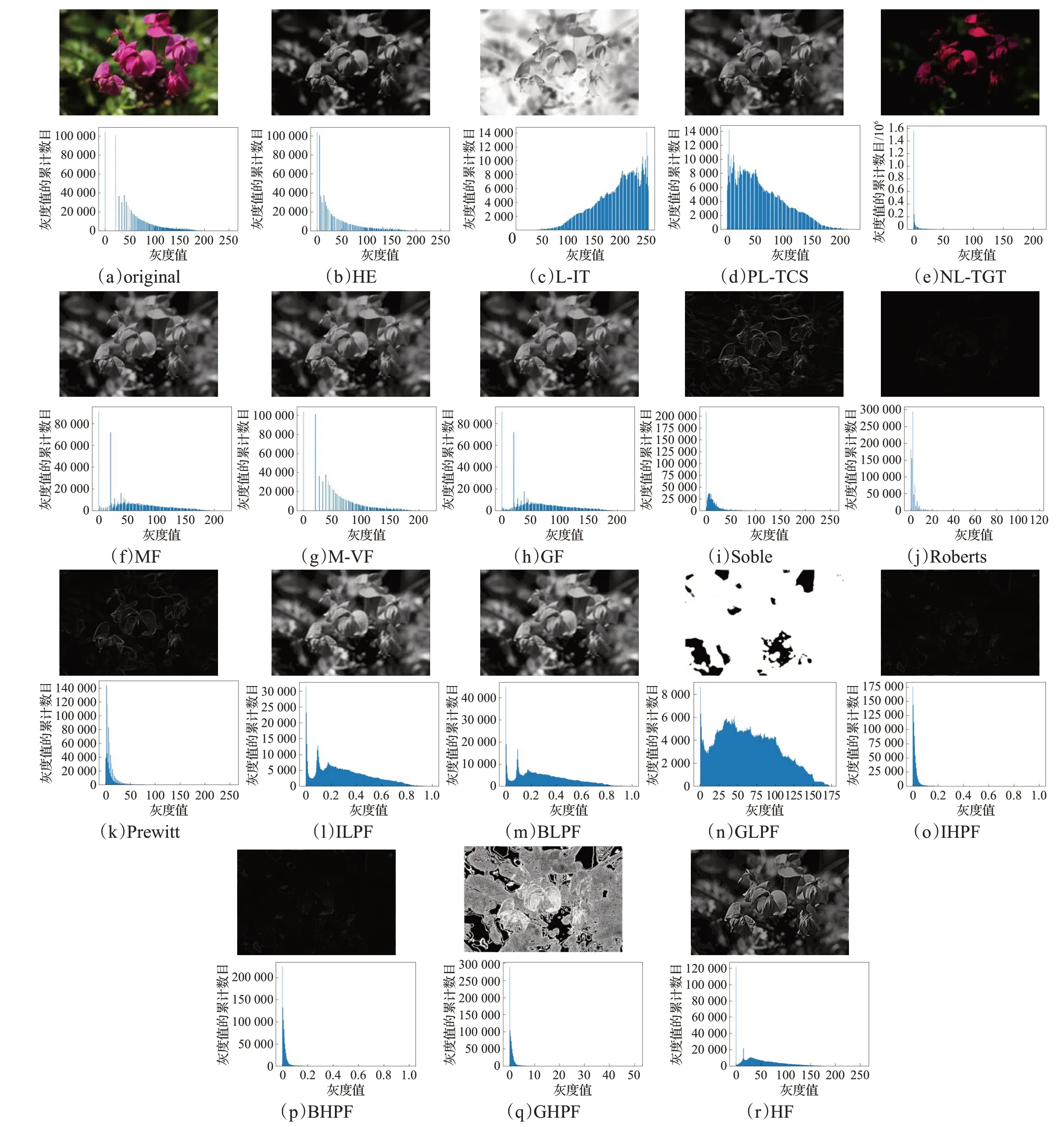
图10 不同算法得到的增强图像及其对应的直方图Fig.10 Enhanced images obtained by different algorithms and their corresponding histograms

由图10可知，从增强图像和其直方图可以看出，HE算法通过拉大图像动态范围达到了图像增强的目的，因此对于动态范围较大的原始图像增强效果不明显。灰度变换类算法能够使得图像整体的亮度值分布较均匀。平滑滤波算法能够使得图像增强后更符合人眼视觉效果。锐化滤波算法能够使得图像增强后对比度更加明显。频域滤波类算法图像增强的效果不佳，说明该原始图像不适宜用该类方法进行图像增强。HF算法效果最好，增强细节的同时也提高了人眼视觉的效果。

3.2 图像增强效果客观评价

本文采用图像的对比度、信噪比和信息熵对增强后的图像质量进行评价。图像对比度的计算公式如下：

式中，δ2(i,j)即相邻像素间的灰度差，Pδ(i,j)即相邻像素间的灰度差为δ的像素分布概率。

图像的信噪比计算公式如下：式中，Gt为图像目标区域最大的灰度值，Gb为图像背景区域的灰度均值，σ为图像背景区域像素灰度值的标准差。

图像信息熵的计算公式如下：

式中，p(k)为灰度级k的概率密度，M为最大的灰度级。

分别采用以上公式计算图像的对比度、信噪比和信息熵，计算结果见表1和表2。

由表1和表2可以看出，直方图均衡化算法能有效提升原始图像的对比度，但由于合并了一些区域，导致了某些图像信息的丢失，使得图像的信噪比和信息熵的提升不够明显。灰度变换类算法同样能提高原始图像的对比度和信噪比，但对于图像的信息熵效果不明显。空域滤波类算法图像的信噪比和信息熵有一定的提升效果，但对于图像的对比度效果不明显。频域滤波类算法图像的对比度、信噪比和信息熵效果度不明显，说明原始图像不适宜用该类方法进行图像增强。同态滤波类算法效果最好，在图像的对比度和信息熵都有明显的提升，但由于增加了高频部分的灰度范围，放大了某些噪声使得增强后的图像信噪比效果不明显。

表1 不同算法得到的图像质量的客观评价结果1Table 1 Objective evaluation results 1 of image quality obtained by different algorithms

表2 不同算法得到的图像质量的客观评价结果2Table 1 Objective evaluation results 2 of image quality obtained by different algorithms

3.3 空频域图像增强方法分析对比

对于空频域图像增强方法，每个方法同样具有自己的优点与不足之处，也有自己的适用范畴。为了综合分析每个算法，对每个算法进行了对比，其详细信息见表3。

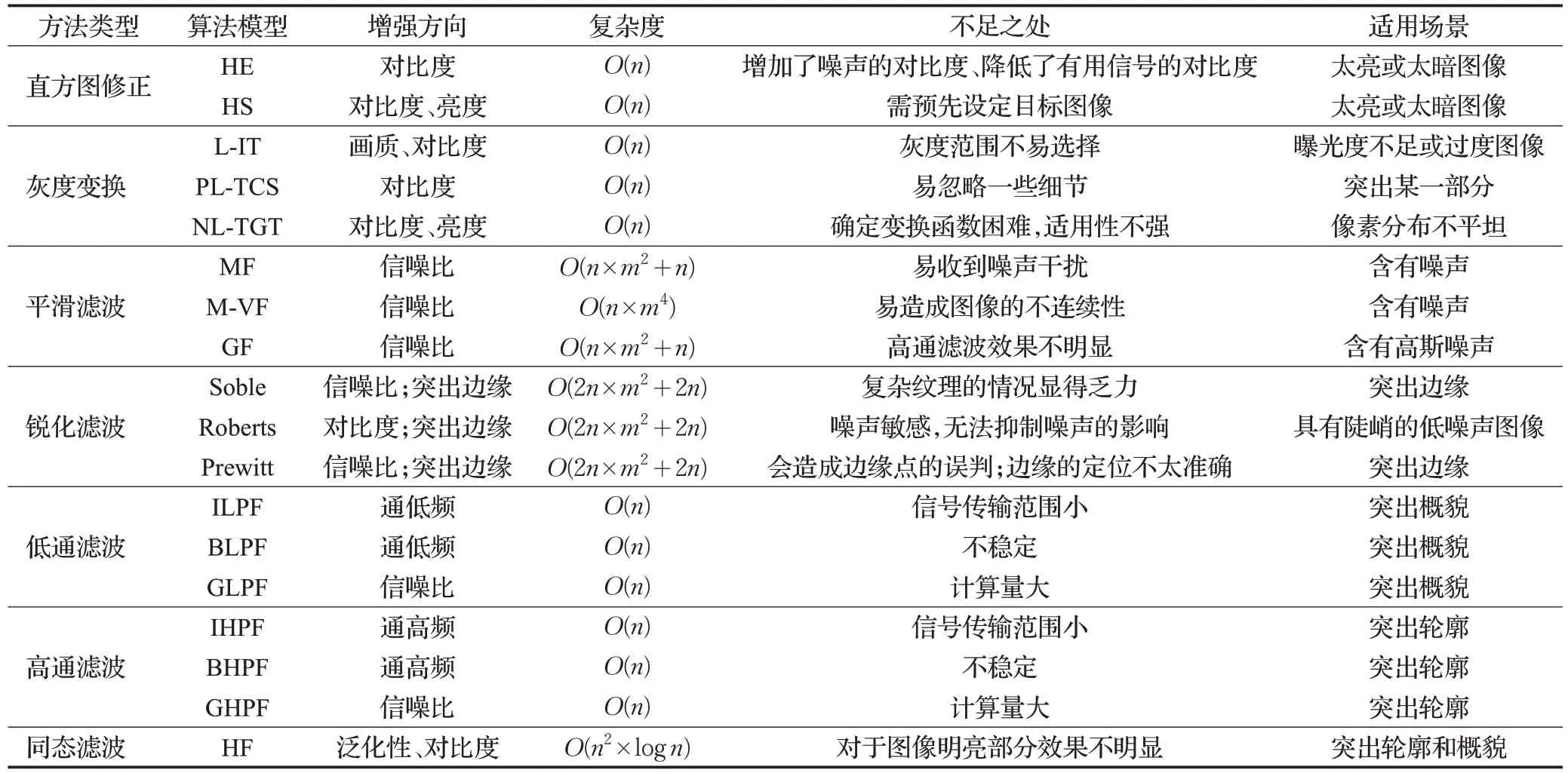
表3 各空频域图像增强方法的分析比较Table 3 Analysis and comparison of various space-frequency domain image enhancement methods

3.3.1 空域图像增强算法模型分析比较

由表3可知，对于基于空域的图像增强方法，主要是对图像对比度、亮度、分辨率和视觉效果进行了增强，在空域图像增强方法中，直方图修正更适合用于曝光过度或曝光不足的图像，但是同时也会产生细节减少、过分增强的问题；灰度变换应用范围更广，更灵活，效果更好，但是相比于直方图函数更复杂，适用性不强，计算更加复杂；平滑滤波更优于处理低频图像，消除噪音，但同样易受噪声干扰，不能很好地保护图像全局细节；锐化滤波更适用处理高频图像或突出边缘图像，但存在边缘定位不太准确，对噪声处理效果不理想等问题。与其他三类方法，直方图计算简单，运行消耗更小，但效果不是特别明显，而灰度变换、平滑滤波、锐化滤波虽然计算量较大，但针对性更强，对于其适用的图像效果明显更优。

3.3.2 空域图像增强算法模型分析比较

由表3可知，对于基于频域的图像增强方法，主要是对图像对比度、色差和饱和度进行了增强，在频域图像增强方法中，低通滤波的优势在于图像平滑，去除噪声，高通滤波的优势在于突出边缘、亮度高的地方，使得特征更加明显，但是低通和高通滤波都不太稳定，信号传输范围较小。而同态滤波综合了两者的优势，且可解决非线性问题，应用性更广，但也削弱了图像的特征表达。

4 结论与展望

本文在阐述图像增强概念的基础上，着重介绍了基于频域和空域两类传统的图像增强方法，选取了不同类别中的代表性算法进行验证和分析，并对其图像增强的效果进行了比较和评价，并对各算法的优缺点、适用场景和复杂度进行了对比分析。

综观图像增强领域的应用场景，针对同一图像，图像增强方法的效果不同，增强对比度更适宜采用空域图像增强方法，突出细节和轮廓更适宜采用频域图像增强方法，所以在实际的图像增强任务中，需根据不同的图像和不同的目标，灵活地选择图像增强算法，以获得最佳的图像增强效果。随着图像增强技术的不断发展，图像增强在计算机图像识别任务中的应用越来越广泛，图像增强的效果也有了明显的提升，但仍然存在一些难题：（1）大部分改进算法仅仅关注一个因素进行改进，往往造成解决了一个因素而很有可能产生了另一个因素，没有综合考虑，适用性不强；（2）多种算法联合使用时，没有考虑算法间的相互影响；（3）研究的改进算法计算较复杂；（4）大部分研究仅仅着重在某一个算法或者某一类算法，没有很好地考虑不同算法相互融合，无法更加有效地发挥各个算法的优势。这些问题将成为未来的研究热点，具有极其重要的研究价值和意义。

本文研究的算法都是经典空频域图像增强算法，但随着图像数据量的扩展，产生质量差的图像也随之增多，因此在未来的研究工作重点可能主要在以下方面：

（1）虽然现阶段已有大量图像增强算法，但是增强效果还不是特别明显，因此设计一个更加高效、适用性强的算法是未来的研究热点，如何提高图像的质量仍然是图像增强领域未来的研究方向。

（2）无论在时间或者空间复杂度上，大部分的研究算法复杂度较高，如何将算法改为最优或者局部最优算法使得复杂度或消耗尽可能小是一直需要研究的方向。

（3）随着图像数据的剧增，导致算法运行时间过度增长，因此采用并行化运算和分布式运算也是下一步可行研究的内容之一。

（4）信息时代新的图像数据每时每刻都在增加，图像增强算法所得到的结果也应要更新，因此，越来越多的改进算法随之诞生，但如何更好地降低甚至消除改进中各算法因素间的相互影响是未来亟需攻克的难关之一。