变异反向学习的自适应帝王蝶优化算法
孙成硕,戚志东,叶伟琴,单 梁
南京理工大学 自动化学院,南京 210094
元启发式算法是基于计算智能的机制求解复杂优化问题最优解的方法,也称为智能优化算法。智能优化是对生物、物理、化学、社会、艺术等系统或领域中相关行为、功能、经验、机理的认识,揭示优化算法的设计原理,在特定问题特征的引导下提炼相应的特征模型,设计智能化的迭代搜索型优化算法。常见的元启发式算法有粒子群优化(PSO)算法[1-2]、差分进化算法[3-4]、布谷鸟算法[5]、萤火虫算法[6]等。PSO算法是一种基于群体智能的全局随机寻优算法,通过模仿鸟类的觅食行为,将问题的搜索空间类比于鸟类的飞行空间,每一只鸟可以抽象为一颗微粒,最优解相当于鸟寻找的食物。差分进化算法是通过选择、交叉、变异更新种群个体,寻找最优解。布谷鸟搜索算法(CS)是2009年剑桥大学杨新社所提出的一种群智能优化算法,它是通过模拟某些种属布谷鸟的寄生育雏这一生物习性,来有效地求解最优问题的算法。萤火虫算法(FA)是把空间各点看成萤火虫,利用发光强的萤火虫会吸引发光弱的萤火虫的特点。在发光弱的萤火虫向发光强的萤火虫移动的过程中,完成位置的迭代,从而找出最优位置。萤火虫算法被应用到几乎所有领域科学和工程,如数字图像压缩和图像处理、特征值优化、工程结构设计、调度和旅行商问题[6-9]。近年来,一些新兴的元启发式优化算法也不断提出,如飞蛾优化算法、麻雀搜索算法等。飞蛾优化算法(MFO)[10]是飞蛾根据光照方向来和自身夹角来调整飞行方向,产生螺旋式逼近光源的飞行路径来搜寻最优解。麻雀搜索算法(SSA)[11]主要是受麻雀的觅食行为和反捕食行为的启发,通过发现者与加入者的位置更新来寻找全局最优解。
受美国帝王蝶在迁徙行为的影响,Wang等[12]提出了帝王蝶优化算法(MBO)。MBO优化算法通过调整算子与迁移算子进行粒子位置更新,两个算子同时进行,一方面增加了粒子的多样性,另一方面权衡了粒子的集中性。适合并行处理问题,且在多领域广泛运用[13-14]。
在一般问题处理中,MBO具有较好的收敛性与较快的运行速度,能较为准确地找到最优解。但由于其调整算子的调整率与迁移率不变,易使问题陷入局部最优解。同时,在一些复杂的测试中,MBO搜寻不到最优的解。故如何避免MBO陷入局部最优解同时不能增加运行的复杂度成为该算法研究方向。
孙林等[15]通过交叉迁移和共享调整对原始MBO算法的局部最优解进行了处理,使其更高效地寻找到全局最优解。Ghanem等[16]将人工蜂群算法与MBO算法结合形成新的元启发式算法。作为新兴的一种算法,上述的改进方法可以提高MBO寻优的性能,但是仍存在问题,如迁移算子更新方式单一,种群的多样性不足,搜索的位置有限等。
针对上述问题,本文基于帝王蝶优化算法,提出了变异反向学习的自适应的MBO算法(adaptive monarch butterfly algorithm based on mutation reverse learning,ALMBO)。首先,在MBO的迁移算子中引入变异反向学习策略,对蝴蝶的位置进行变异更新,增加种群的多样性,避免算法陷入局部最优解。然后,将MBO的调整算子改成自适应的调整算子,使MBO中的调整算子随着迭代次数的变化进行线性调整,提高了算法适应度,增强算法的寻优能力。通过实验对比本文所提出的算法与其他类似算法的寻优能力,验证ALMBO的有效性。
1 帝王蝶优化算法
帝王蝶作为最常见的北美蝴蝶之一,其翅膀上橙色和黑色花纹很容易辨认。研究者们发现,帝王蝶每年春天都会迁移数千英里从加拿大南部飞往墨西哥的中部地区,到了秋季又会往相反的方向飞行,其迁徙能力在蝴蝶纲目中首屈一指。
MBO是模仿帝王蝶的迁移行为来解决各种优化问题,可将其迁移规律理想化为如下假设:
(1)所有的帝王蝶只分布在Land1和Land2中。Land1和Land2是种群所在地。
(2)每只小帝王蝶个体是由Land1和Land2的帝王蝶的迁移算子生成的。
(3)保持种群数不变,即老的帝王蝶在更新为新的小帝王蝶时死去。但若新的小帝王蝶适应度不如老的帝王蝶,则抛弃新的小帝王蝶,保留老的帝王蝶。
(4)适应值最优的帝王蝶会自动迁移到下一代,保证其帝王蝶的质量。
1.1 迁移算子
新的帝王蝶是通过迁移算子从Land1和Land2的帝王蝶中产生。Land1中的帝王蝶代表种群1,Land2中的帝王蝶代表种群2。其中种群1的数量为:
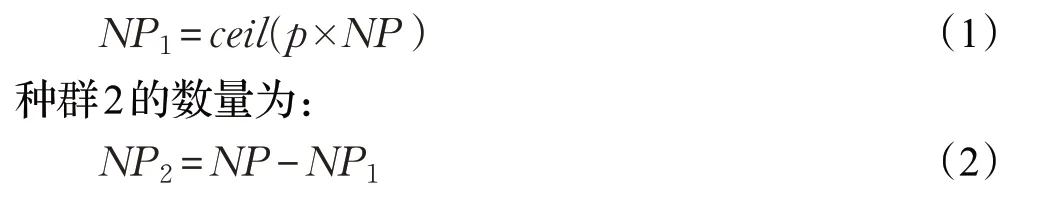
其中,NP为Land1和Land2总的种群数,p为种群1与种群2中帝王蝶的比例,p=5/12,ceil(x)为舍入到大于或等于x的最接近的整数。
设定Land1和Land2中的子群分别称为亚种群1和亚种群2,则迁移过程可以表示为:

其中,rand为[0,1]的随机数,peri表示为迁移周期,取值为1.2。
1.2 调整算子
MBO中的调整算子是用来更新亚种群2中帝王蝶的位置。其位置更新可以表示为:

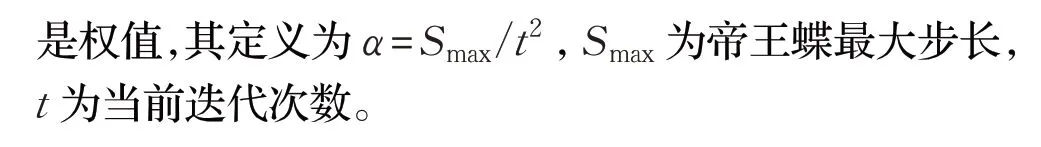
2 变异反向学习的自适应的MBO算法
2.1 变异反向学习迁移算子
原始MBO中,帝王蝶每次位置更新是基于亚种群1和亚种群2中已有的粒子进行重新选择,但个体的数量有限,选择性与随机性不大。生成的粒子不具有多样性,且生成的粒子易陷入局部最优解。故本节,受遗传算法中变异概率思想的启发,将变异概率与反向学习策略进行结合,对帝王蝶的位置进行干扰更新,增加种群的多样性同时加快了收敛的速度。
反向学习(opposition-based learning,OBL)是Tizhoosh[17]于2005年提出的数学方法,其本质使通过估计和比较可行解及其反向解,选择最好的解进入下一次迭代。反向学习的数学表征为:

其中,a,b分别是(a,b)区间中的上下限,c是源数,P是源数的反向数字。
反向学习的引入使收敛速度加快。优化算法的计算时间与初始种群中个体与最优个体的距离有关,个体若在最优值附近出生,则这一次的迭代计算中种群的所有个体都会进行快速的收敛。而纯随机生成的个体由于没有进行过估计,收敛速度是无法预知的。
故本文将变异反向学习融入MBO算法中,其数学表达式为:

2.2 自适应调整算子
在原始的MBO优化算法中,迁移率p与调整率BAR是一个固定值,在整个迭代中都不会发生变化。这样就使得在Land1和Land2中的帝王蝶通过调整算子进行局部更新时,易陷入局部最优解。同时,调整算子生成的所有亚种群个体都直接被接受,继承的方式过于简单。因此,为使种群多样化,将自适应的策略引入到调整算子中,形成自适应调整算子,其公式如下:

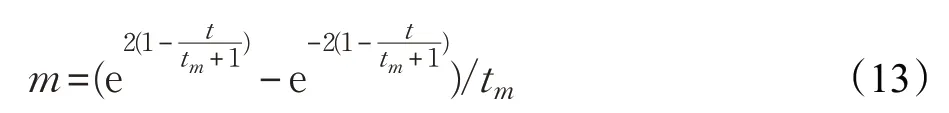
其中,t m是当前最大迭代次数,BARmax、BARmin是调整率的上下界,其范围为[0,1]。为扩大参数选取的范围,设定BARmax=0.8,BARmin=0.2。同时,在第一次迭代的过程中,迁移率p与调整率BAR取5/12。
2.3 柯西变异扰动
柯西变异的理论基础是柯西分布函数,一维柯西分布的概率密度如图1所示。
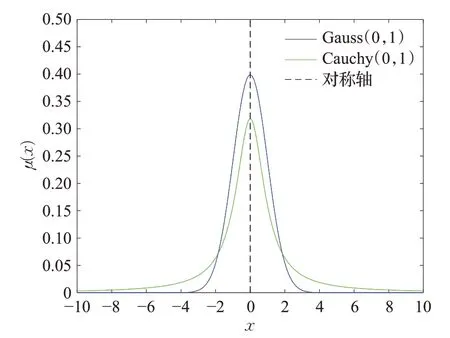
图1 概率密度曲线Fig.1 Probability density curve
柯西分布在两端趋于0的速度较缓,且过程较为平稳,其原点附近的峰值与高斯原点附近的值相比较小,所以柯西变异在扰动能力方面比高斯变异更强。引入柯西变异扰动可以提高算法全局的搜索能力,防止陷入局部最优解。在每次更新的种群中,将排序在最后的5只帝王蝶进行柯西变异,使变异个体附近生成更大的扰动,使整个群体在更大的范围内进行寻优。其算法表达式为:
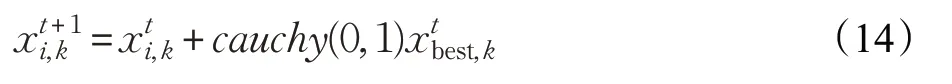
其中,柯西随机变量生成函数为η=tan(π(ξ-0.5)),ξ∈rand(0,1)。
2.4 算法流程图与步骤
由于MBO易陷入局部最优解,故本文针对这一问题,提出了变异反向学习策略扩大种群的多样性,提高其收敛性。同时,对于原始MBO算法中迁移率与调整率固定,本文提出了自适应的调整算子,在优化的过程中对帝王蝶的调整率进行线性调整,增强算法的寻优能力。最后,将每次适应度排在最后的5个粒子进行柯西变异扰动,摆脱其局部最优解,更大程度上激发粒子寻找全局最优解的潜力。算法的流程图如图2所示。
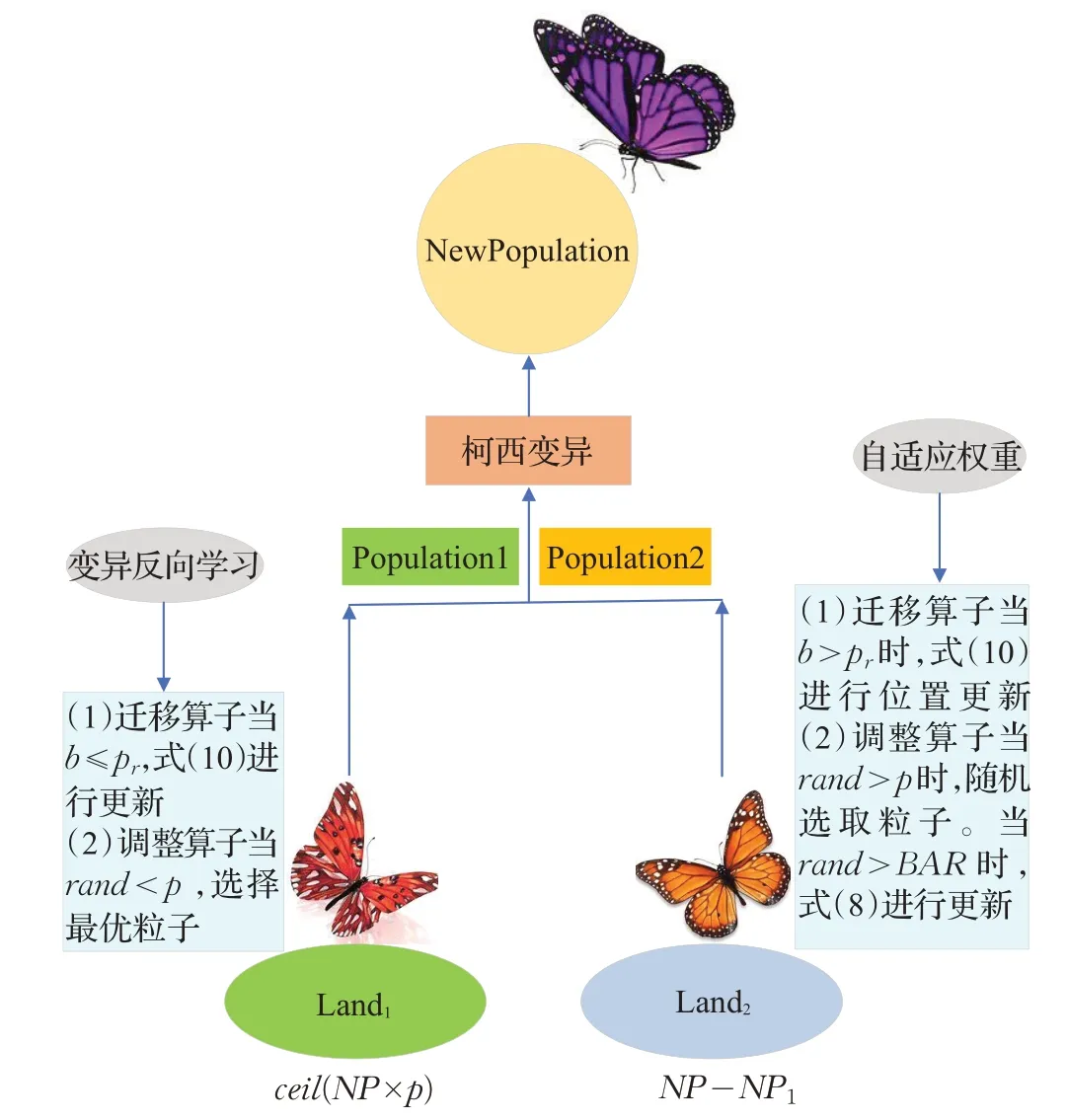
图2 ALMBO算法流程图Fig.2 Flow chart of ALMBO algorithm
2.5 时间复杂度的分析
时间复杂度反映了算法的运行效率。设种群数为N,亚种群1规模为N1,则亚种群2规模为N-N1,优化问题维度为D维,参数初始化为O(1),计算函数适应度为O(N),迭代过程中种群复杂O(ND)。其复杂度计算公式如下:
(1)计算帝王蝶函数的适应度所需为O(N)。
(2)排序的时间复杂度为O(N2)。
(3)帝王蝶分成了2个子群,时间复杂度为O(N)。
(4)在迁移算子中的引入变异反向学习策略,有2个内循环,时间复杂度为O(DN1)。
(5)在调整算子中引入自适应策略,存在2个内循环,时间复杂度为O(D(N-N1))。优化算法ALMBO总时间复杂度为:
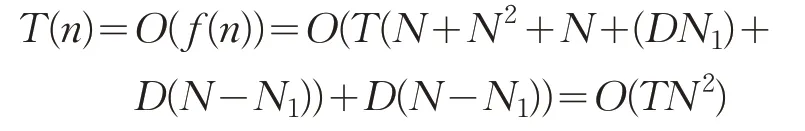
上述分析可知,ALMBO算法在时间复杂度上与原始MBO时间复杂度是相当的。
2.6 收敛性分析

引理1波莱尔-坎泰利(Borel-Cantelli)设B1,B2,…,B n是概率空间上相互独立的事件系列,p(B k)是每个事件系列对应的概率,则有:
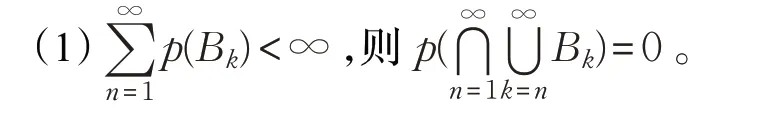
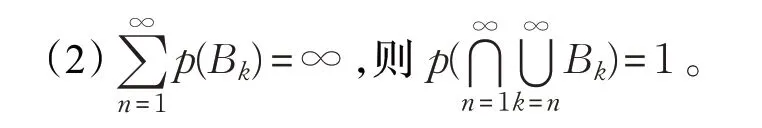
定理1ALMBO算法中的解序列{X t,t≥0}是有限状态空间的齐次马尔科夫链。
证明ALMBO算法在状态转移过程中都是在有限空间中进行的,算法中的变异反向学习迁移,自适应调整,柯西变异干扰等操作都是满足独立随机的过程,并且整个迭代进化过程都是采取的保留最优个体的机制,第t+1代的种群Qt+1只是受第t代种群Q t的影响,与种群之前的信息无关。因此{X t,t≥0}是有限状态空间的齐次马尔科夫链。
引理2在ALMBO算法的状态空间中,存在常数μ∈(0,1),使条件p ij<μ成立,p ij表示从状态空间A i转移到状态空间A j的概率[19]。
定理2ALMBO优化算法以概率1收敛到全局最优解。

3 实验及结果分析
3.1 参数设定
实验选取文献[20]、文献[21]中典型的8个基准函数测试ALMBO的性能,如表1所示。同时为验证其性能,选择飞蛾优化算法(MFO)、麻雀搜索算法(SSA)、PSO优化算法以及MBO算法进行比较。实验环境为Windows10,64位操作系统,CPU为Inter Core i5-6500H,主频为3.2 GHz,内存8 GB,算法是使用MATLAB-2014b,使用M语言编写。为保证对比的公平性,算法基本参数设置相同:种群规模为50,测试函数维数30/50,最大迭代次数为1 000次,各算法独立运行50次。
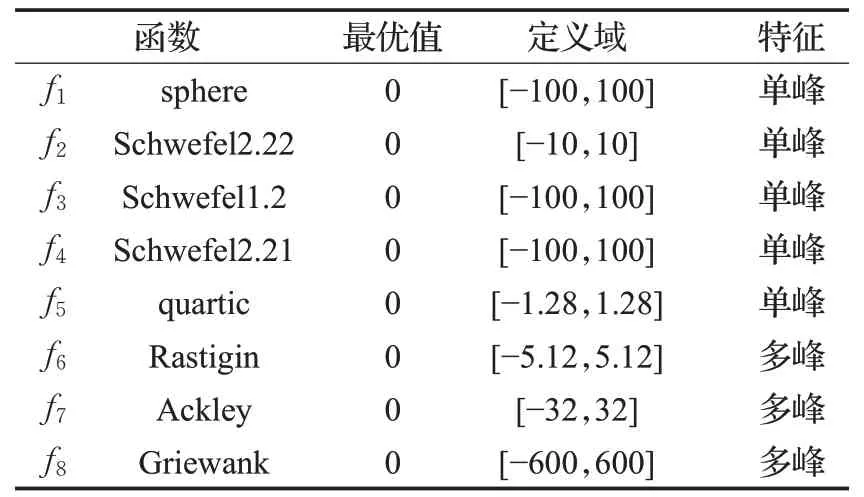
表1 基准函数Table 1 Benchmark function
3.2 算法性能分析
5种优化算法的8个基准函数的测试结果如表2和表3所示。通过对表2和表3的结果分析,MFO、SSA、MBO对于单峰函数问题求解上具有较强的搜索能力,精度较高。在对于多峰函数优化问题求解时,其局限性就体现出来,其求解精度不理想。PSO优化算法同样如此,对于多峰函数寻优效果更差。而本文所提出的ALMBO算法无论在30维或50维,多峰或单峰在求解精度上都比其他四种优化算法要高。对于30维的f2、f3与f5函数可以搜到理论最优值0。ALMBO在多次寻优的平均值与标准差都优于其余四种算法,但在50维f7多峰函数的寻优中,其余四种算法陷入了局部最优解,故每次寻优结果相近,标准差小。ALMBO虽标准差大于其余四种函数,但其可以跳出局部最优解,寻优精度高于其余四种算法。故认为引入变异反向学习与自适应策略有助于算法搜寻最优值,规避了局部最优解,防止算法在不同程度上早熟。同时,在种群更新中引入柯西变异干扰,保持了其多样性,获得了较好的寻优能力。
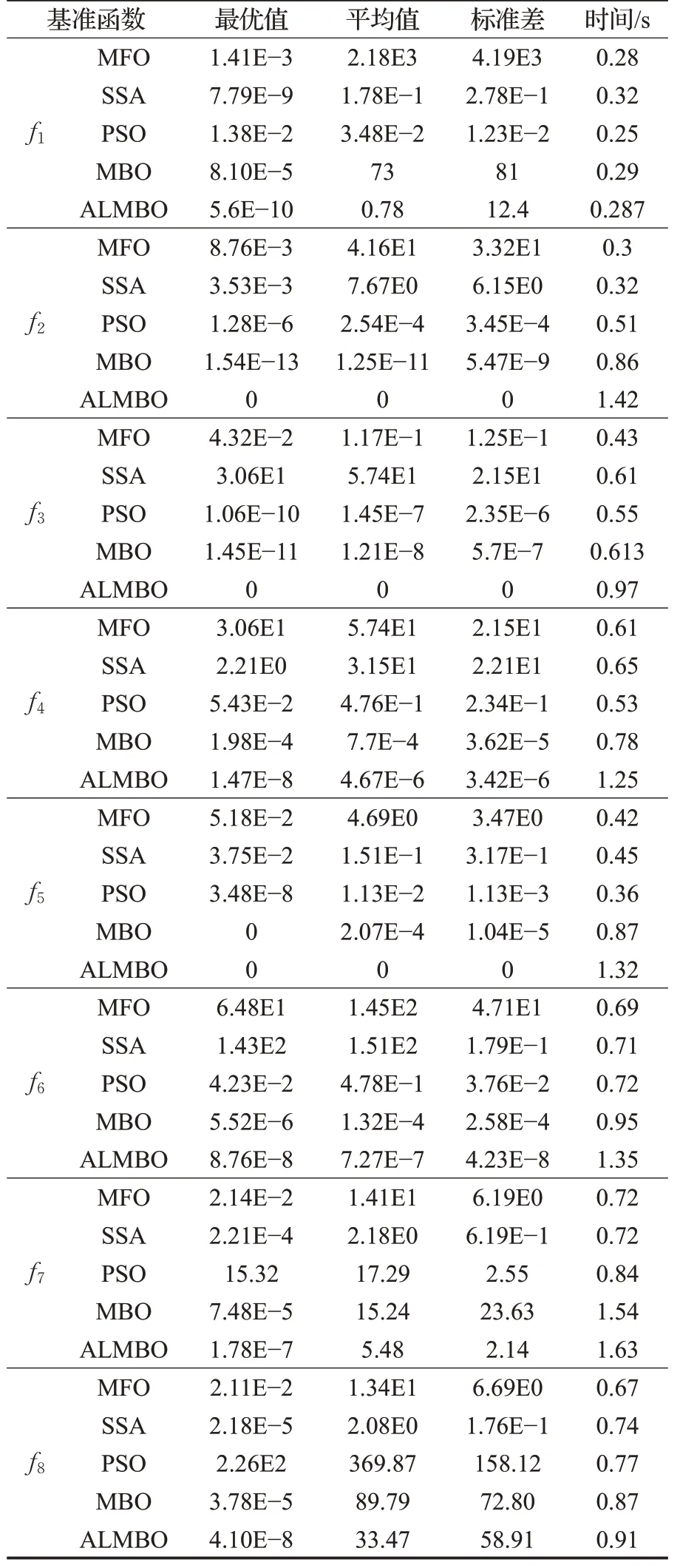
表2 30维结果分析Table 2 Analysis of 30 dimensional results
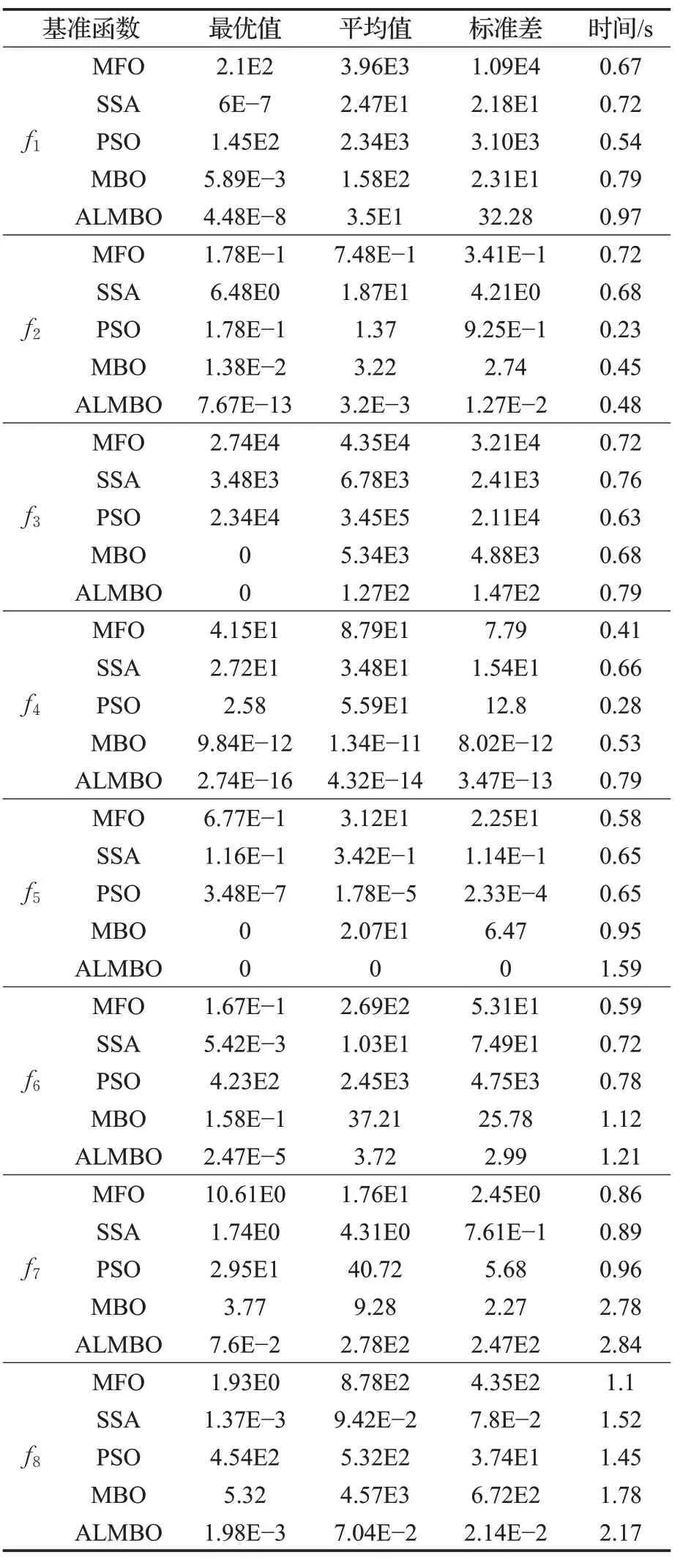
表3 50维结果分析Table 3 Analysis of 50 dimensional results
在寻优时间上,PSO算法因其算法结构简单,故平均耗时最短。MBO与ALMBO引入了调整算子与迁移算子,同时ALMBO在算子上进行了处理,故这两种优化算法的平均耗时比PSO、MFO要长。但从表2可以看出,在30维情况下,ALMBO的平均耗时与MBO相比不超过0.3 s。在50维情况下,ALMBO的平均耗时与MBO相比不超过0.4 s,虽稍牺牲了些寻优时间,但其时间在可接受的范围内。
3.3 Wilcoxon秩和检验
上一节通过最优值、平均值与平均耗时等指标对5种优化算法进行了比较,但仅通过50次独立运行的最优值、平均值是不能较信服地说明ALMBO算法的优越性,故需要进行统计检验来说明本文所提出的算法与其他算法相比有显著性的差异。采用Wilcoxon秩和检验来验证ALMBO每次运行结果在p=5%的显著性水平下与其他算法是否有显著性差异,当p>5%时,可以认为接受假定H0,即认为两种优化算法之间不存在显著性差异,算法寻优能力相当;当p<5%时,则拒绝假设H0,即两种算法之间存在显著性差异。表4是ALMBO与MFO、SSA、PSO、MBO在显著性水平p=5%,维度50维下的比较结果。由于算法自身无法跟自身性能相比,故用N/A来表示。从表4可以看出,检验的p值大部分都远小于5%,故认为ALMBO与其他四种算法存在显著性差异,并且ALMBO的算法显著性更佳。
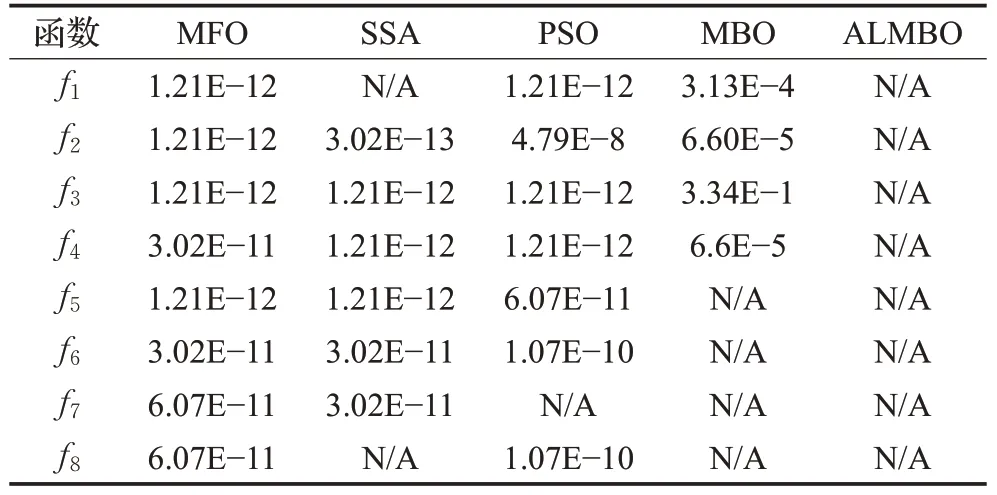
表4 Wilcoxon秩和检验的p值Table 4 Wilcoxon rank and p value
3.4 收敛性分析
图3给出了在30维的条件下8个基准函数的平均收敛曲线图。为方便地观察收敛的情况,对寻优的适应度值(纵坐标)取10为底的对数。由图3(a)至(h)中可以看出,对于单峰函数(图(a)~(e)),MFO、PSO等可以达到较高的精度,而对于多峰函数,其收敛精度明显下降。而无论是单峰函数还是多峰函数,对于每一个基准函数,ALMBO比其他优化算法的收敛精度和速度都要好。图(c)与图(e)分别为在迭代次数300次与500次内搜索到最优值0,故在图中后部分没有显示。由此说明,ALMBO具有较强的搜索能力,能够快速地跳出局部最优解向全局最优解靠近。
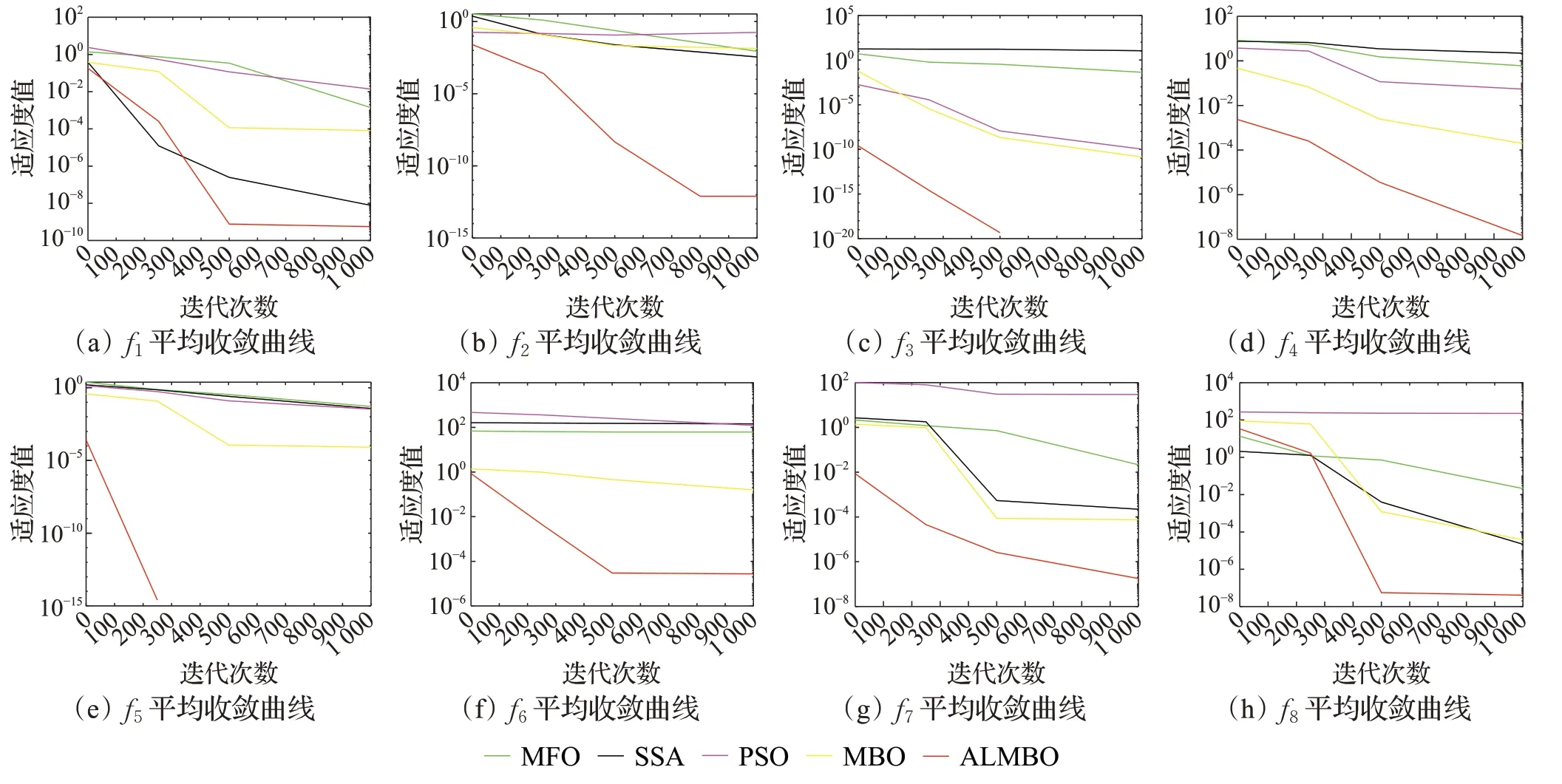
图3 f1~f8平均收敛曲线Fig.3 Mean convergence curves of f1~f8 strategies
4 总结
本文在原始帝王蝶算法的基础上,引入了变异方向学习策略、自适应权重以及柯西变异,提出了一种改进的变异反向学习的自适应帝王蝶优化算法。并将ALMBO与MFO、SSA、PSO、MBO算法在30维/50维的8个基准函数进行对比检验,同时,还运用了Wilcoxon秩和检验的方法,通过显著性水平来验证ALMBO算法的优越性。实验表明,ALMBO可以获得更好的全局最优解与收敛速度。在未来的研究中,考虑将算法应用到系统辨识与滚动优化中,以进一步验证算法的性能。

