改进贪婪投影三角化算法的激光点云快速三维重建

刘翔宇,王 健,常清法,王效盖

(1.山东科技大学测绘与空间信息学院,山东 青岛 266590;2.山东黄金矿业(莱州)有限公司焦家金矿,山东 烟台 261441)

1 引 言

三维重建技术在逆向工程、数据可视化、计算机视觉、医疗技术等领域得到了广泛的应用[1]。该技术发展至今,已经取得了一定的研究成果。根据点云三维重建的方式不同,将三维重建技术分为[2]:参数曲面重建、隐式曲面重建[3]和网格曲面重建。基于参数曲面重建的方法主要包括B样条曲面重建[4]和NURBS曲面重建[5],因为该类方法在进行重建时需要对点云数据进行参数化,而散乱点云数据的参数化效果非常差,所以在对该类数据进行重建时就会造成重构出的模型存在孔洞问题,因此该类方法只适用于表面光滑、变化较小的物体重建。张丹丹等人在传统的NURBS曲面重建基础上提出一种基于点云的整体参数曲面重构方法,该算法采用八叉树建立点云间拓扑关系,然后基于法矢和曲率进行点云精简,该方法提高了整体重建效率并且重建效果较好,但是对于数量较少的点云重建效果不佳[6]。隐式曲面重建的方法主要有泊松算法[7]和移动立方体算法[8],该类算法可以很好的将结构简单的物体拟合成光滑的曲面,但是对于外表结构复杂的物体不能达到理想的重建效果,并且该类算法在进行重建时耗时较长。刘涛等人提出一种基于点云增强优化的泊松重建算法,该算法首先对点云进行降噪处理,然后使用双三次样条插值拟合曲面,该方法有效的减少了模型孔洞的生成,但是在耗时上有所增加[9]。网格曲面重建在点云三维重建中应用最为广泛,经常用于重建具有复杂结构的物体,贪婪投影三角化算法[10](以下简称贪婪投影算法)是网格曲面重建算法的主要代表算法之一,它是基于三维Delaunay三角形的曲面重建方法,贪婪投影算法能够很好的重建出具有复杂拓扑结构的物体,但存在耗时长且对大量点云数据进行重建时模型会出现孔洞的问题。

针对贪婪投影算法的缺点,许多科研工作者做了一些相应的研究。李学兵等人提出一种广度优先搜索算法来调整点云法向量方向,并在此基础上对点云进行重建,该方法得出的模型效果要高于传统贪婪投影算法,但在耗时上有所增加[11]。杨玉泽等提出一种基于KD树纹理映射的贪婪投影算法的点云重建方法,该方法重建出的模型在细节表达上效果较好,但存在点云缺失与孔洞的问题[12]。张津铭等人提出使用移动最小二乘算法对点云数据进行平滑处理,该方法虽然可以去除噪声点的干扰,但也丢失了物体一部分细节特征,导致重建后的模型出现了孔洞[13]。

针对以上问题,本文提出一种改进的贪婪投影算法,期望解决重建后的物体表面粗糙和孔洞问题,并且减少物体重建的时间,提高重建的效率。

2 贪婪投影算法

贪婪投影算法的基本思想是:首先计算输入点云的法向量并在计算完成后投影到某一平面上,然后对投影后的点云作平面内的三角化,从而得到各个点的连接关系。该三角化的过程是基于生长法的曲面重建,该方法通过选取一个样本三角片作为初始曲面,通过对该曲面边界进行延伸,直到形成一张完整的三角网格曲面后结束,然后通过某一平面上的投影点云的连接关系,并以此为基础形成原始点云间的拓扑连接,最后得到重建后的曲面模型。但是贪婪投影算法在进行重建的过程中,如果遇到的点云存在表面不够光滑、密度不均匀的情况,使用该算法得到的重建模型达不到预期效果。贪婪投影算法流程:

1)针对输入点云中的任一点q,采用KD树的近邻域搜索算法确定其含有k个近邻点的邻域。根据搜索的结果,点云会根据其状态分为自由点、完成点、边缘点及边界点。

2)确定任一点q及其k个邻域点的投影切平面,并将这k个邻域点投影到该二维平面中。

①针对第一步中输入的任一点q的邻域,此邻域内的点与过q点的切平面投影存在一一对应的关系。根据贪婪投影算法的PCA(Principal Component Analysis)法线估计方式计算每一点的近似法向量,通过平面方程式来解算出该点的切平面。假设点N0(x0,y0,z0)的法向量m=(A,B,C),点N(x,y,z)过N0的切平面可以表示为:

A(x-x0)+B(y-y0)+C(z-z0)=0

(1)

②为了将空间中的点投影到二维切平面∏中,一般采用投影矩阵的方法,通过平移和旋转等一系列操作得到三维点在切平面上的投影(如图1所示)。投影矩阵ΤM∏的公式如下:

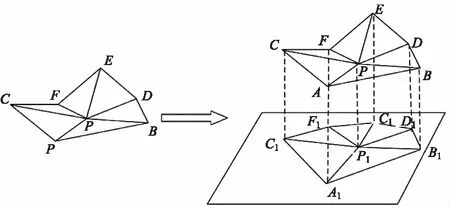
图1 三维k邻近点的局部投影图Fig.1 Local projection of three dimensional k-nearest points

ΤM∏=Tc·Rx·Ry

(2)

其中,Tc为平移变换矩阵:

Rx为围绕x轴旋转α度:

Ry为围绕y轴旋转θ度:

通过式(1)和式(2)可以求出任一点q(xi,yi,zi)在其切平面∏上的投影:

(3)

3)对该二维平面上的点使用贪婪投影算法进行三角剖分,并且每次都选择局部最优点作为扩展点,再通过投影关系,将其扩展的点映射回空间,不断重复这一过程,最终完成物体的表面重构。

步骤一:在点云数据中选择任一点qi作为初始生长点,使用KD树算法搜索其近邻点,在其邻域内找到距离qi最近的点qj并使用直线进行连接,得到线段qiqj,并将其作为三角形的一条生长边。

步骤二:计算距离边qiqj最近的点qk,然后构造出第一个三角形Δqiqjqk。如图2(a)所示。

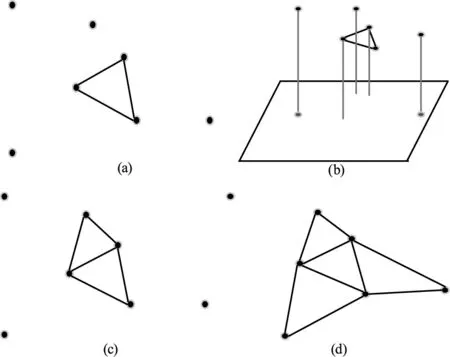
图2 贪婪投影三角化流程图Fig.2 Greedy projection triangulation process

步骤三:在步骤二的基础上,继续寻找距离三角形Δqiqjqk任一边最近的点,构成新的三角形。如图2(c)所示。

步骤四:重复步骤三,直到所有点被选择完毕并构建出完整的拓扑结构,则算法结束。如图2(d)所示。

该算法的原理并不复杂,但是在实现过程中存在一些问题:①使用KD树邻域搜索算法需要耗费大量的时间进行回溯,延长了重建的时间;②当需要重建的物体表面点云密度不均匀时,使用该算法会产生错误的拓扑结构,从而导致重建效果不理想;③当重建物体表面过于复杂时,该算法难以确定投影点与三维空间中的点对应的位置关系,所以会丢失一部分物体信息,造成曲面重叠并使重构后的模型出现孔洞。

3 改进的贪婪投影算法

3.1 体像素(Voxel Grid)网格滤波

体像素网格滤波的基本原理是:根据输入的点云数据建立三维体素栅格,三维体素栅格是一种微小的空间三维立方体的集合,通过设定采样距离的参数大小,可以将这些三维立方体等距划分为a·b·c个立方体,并将输入的点云数据划分到立方体中,将这些包含点云的立方体看成是子包围盒,剔除掉主体之外的所有立方体,最后计算这些主体中所有点的重心,并使用该重心近似代替这些点。该方法在思想上简单并且易于实现,对于散乱无序的点云不需要再次建立点云间的拓扑关系,减少了计算量,加快了算法的重建速度。

3.2 八叉树优化

八叉树最初由Hunter博士提出,该方法被广泛用来表示三维空间,是四叉树在空间范围内的推广[14]。八叉树在对点云进行管理时所采取的思想是:八叉树根据全部点云的最小外接包围盒建立根节点。然后根据等分原理将外接包围盒等分为8个小立方体,也就是子节点。在对点云进行归类的过程中,根据位置关系将其划分到对应的子节点中。至此,三维点云数据已经按照各自特性剖分完毕。八叉树算法在搜索大规模点云时,效率要高于KD树,并且自动化程度较高,可以对点云三维重建的时间进行优化。图3为八叉树的结构示意图。

图3 八叉树结构图Fig.3 Octree structure diagram

3.3 移动最小二乘算法(Moving Least Squares,MLS)基本原理

3.3.1 拟合函数的建立

在拟合区域的局部子域上,拟合函数f(x)表示为:

=pT(x)a(x)f(x)

(4)

其中,a(x)=[a1(x),a2(x),…,am(x)]T为待求系数;p(x)=[p1(x),p2(x),…,pm(x)]T为基函数；它是一个k阶完全多项式；m是基函数的项数。对于一维问题,它的基函数为p(x)=[1,x,x2,…,xm]T,对于二维问题,线性基为p(x)=[1,x,y]T,m=6,二次基通常为[1,x,y,x2,y2,xy]T,m=6,为了尽可能获得更精确的局部逼近,有必要将f(xi)与节点值yi的局部逼近之差的平方权值最小化。因此,离散加权范式为:

(5)

其中,n是影响区域的节点数;f(x)是拟合函数;w(x-xi)是节点xi的权函数。为了确定系数a(x),式(2)中pT(xi)a(x)-yi应取极小值,从而得:

a=(BWBT)-1BWy

(6)

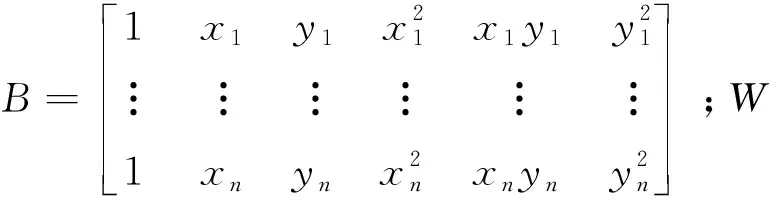
通过式(6)可以计算出式(4)中的各项系数,将未知点代入式(4)中,就能求得该未知点的拟合函数值。

3.3.2 确定权函数

权函数作为移动最小二乘法中最重要的部分,权函数w(x-xi)在移动最小二乘法中具有紧支性,即权函数在x的子域内不为0,这个子域外全是0,这个子域为x的影响域(即权函数的支持域),其半径记为Smax。选择权函数时应遵循以下原则:

①权值函数的紧支决定了各节点在支持域中的权值大于0,在支撑区域外或边界处的权值等于0。

②必须有单位分解。

③权函数要光滑连续,可以推导出函数。

④在支撑域中,随着‖x-xi‖的增加,权值减小。

(ⅰ)点云平滑处理

常用的权函数是三次样条权函数,其表达式为:

(7)

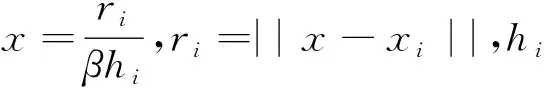
(ⅱ)点云重采样

在空间点云数据重采样中,重采样点的位置会相对于起始采样点发生变化,因此权因子w(x-xi)也应随着待求点位置的变化而变化,针对这种情况,本文使用如下权函数:

(8)

式中,di(x)表示第i个原始采样点pi与重采样点p之间的距离；u表示影响区域中的特征与重采样间的影响因子。

通过式(8)权函数对式(6)进行计算,求得该拟合函数的系数矩阵。

α(x)=(BW(x)BT)-1BW(x)y

(9)

式中,W(x)为高斯权函数的对角矩阵。

3.4 基于改进的贪婪投影三角化的重建流程

传统的贪婪投影算法在估计法向量时采用的是PCA算法,该算法在估计法向量时的正确率不高,造成重建时出现错误的拓扑结构；在处理大规模点云时,KD树的搜索效率要低于八叉树。因此本文的改进算法采用基于MLS法向量估计算法来进行法向量计算并进行重建,并且使用八叉树来代替KD树进行近邻域搜索(如图4所示)。具体的步骤流程如下:

图4 本文算法流程Fig.4 The Algorithm Flow of This Paper

步骤一:对原始点云采用体像素网格滤波算法进行下采样,实现点云的简化并保持密度均匀。

步骤二:针对步骤一中得到的点云表面粗糙,传统贪婪投影算法不能很好地进行平滑处理,所以采用MLS算法对点云进行平滑及重采样处理,得到表面更加平滑的点云数据。

步骤三:对步骤二生成的点云,采用基于MLS算法的点云法线估计的贪婪投影算法对点云进行重建,并且使用八叉树来代替KD树进行近邻域搜索,最终得到效果较好的曲面模型。

4 实验验证与精度分析

为了验证本文算法的有效性和可行性,在本次实验中,实验平台的软件开发工具为Windows10操作系统、vs2019、pcl1.11.0,以及处理点云所需的CMAKE、VTK、boost库等。实验数据选用两种数据源:分别为斯坦福大学的标准数据集horse和通过Trimble TX8三维激光扫描仪获取的雕塑数据。如图5所示。

图5 实验数据Fig.5 Experimental Data

为了体现出改进算法的性能,对比了泊松算法、传统贪婪投影算法和本文算法的重建时间和不同点云数据预处理前后的点云数量变化,如表1和表2所示。从表1可以看出泊松算法的重建时间要长于传统贪婪投影算法和改进算法,由于泊松算法需要使用移动立方体算法原理来提取等值面,所以耗时更长。本文算法的重建时间比传统贪婪投影算法减少了约30 %、比泊松算法减少了约45 %,效率提升明显。

表1 三种算法耗时对比Tab.1 Time consuming comparison of three algorithms

表2 点云预处理前后的数量变化Tab.2 Comparison of the number of point clouds before and after pretreatment

图6为预处理后的horse数据和雕塑数据分别进行传统贪婪投影算法的法线估计和MLS算法的法线估计,由于传统贪婪投影算法与泊松算法的法线估计方法一致,故不加入对比。分析图6(a)和图6(b)与图6(c)和图6(d)可以发现,在模型的边缘、角点、horse数据的腿部和雕塑数据的手臂处,传统贪婪投影算法的法线方向估计一致性较差,MLS算法在这几处地方的法线估计一致性要优于传统算法,所以使用MLS算法进行法线估计可以为后期的重建提供一个更加准确的法线输入,提高重建的精度。

图6 法线估计可视化Fig.6 Visualization of normal estimation

将两组点云数据分别应用泊松算法、传统贪婪投影算法和本文算法进行重建效果比对。重建结果如图7、8所示。从图7(a)和图8(a)可以看出,泊松重建无论是在细节处,还是在模型的完整度上,都不如贪婪投影算法的重建效果好,并且在雕塑数据重建时出现了伪平面,这是由于泊松算法适用于具有封闭性的点云。分析图7、图8中的(b)、(c),对于标准horse数据,由于其整体结构简单,重建的效果差异不大；对于雕塑数据,由于其结构复杂,对点云进行体像素网格滤波重建后,效果要明显好于直接使用贪婪投影算法进行重建,这是因为原始点云中包含许多冗余点,在进行法线估计时会产生错误的结果,从而导致孔洞的产生。分析图7、图8中的(c)、(d)可以看出,经过体像素网格滤波和MLS算法的平滑与重采样后,标准horse数据和雕塑数据生成的模型均在细节处表达出了更好的效果。最后使用本文改进的算法和传统贪婪投影算法进行重建,对比图7、图8的(a)、(e)可以看出,在horse数据的头部和腿部处保证了细节不丢失,并且孔洞有所减少；雕塑数据在保证手臂和大腿处的衣服褶皱不丢失的基础上,提高了模型整体的平滑效果,并且有效的减少了孔洞的产生,而且在面部和衣服等位置处保持了较高的网格细节。通过以上分析可以得出本文改进的算法重建出的模型孔洞少、表面更加光滑、细节表达效果也较好。

图7 Horse重建效果Fig.7 The effect of horse reconstruction

图8 雕塑重建效果Fig.8 The effect of sculpture reconstruction

采用4个定量分析精度评价指标,即利用Geomagic Studio软件计算点云到模型实体的最大偏差距离、平均偏差距离、标准差和均方根误差,并且使用该软件显示三种算法生成模型面片的数量,以此对三种算法生成模型的重建结果进行精度评价。如表3、表4和表5所示。由于horse数据结构较为简单,三种算法重建精度差异不大,在三角面片生成数量上,本文算法也要少于其他两种算法。对于采集的雕塑数据,由于其结构复杂,本文算法在精度上相比于泊松算法要提升了1.13 mm,相较于传统贪婪投影算法提升了0.53 mm,在生成三角面片的数量上本文算法也要优于泊松算法和传统贪婪投影算法,通过分析可以得出本文算法满足大多数领域中建模的精度要求。

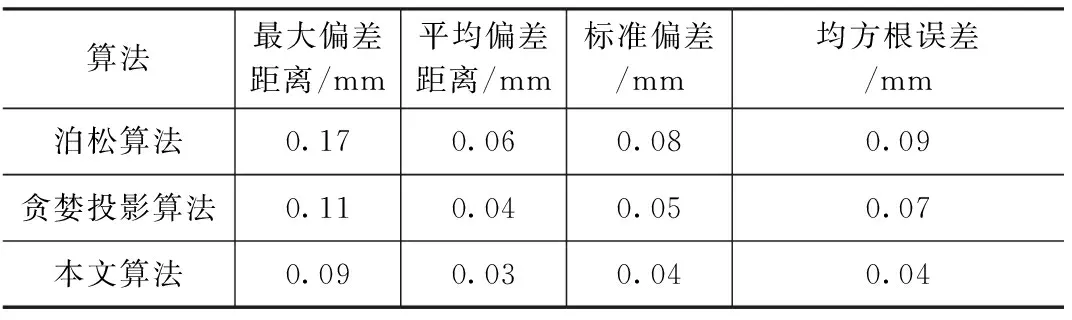
表3 Horse模型重建精度分析Tab.3 Accuracy analysis of horse model reconstruction

表4 雕塑模型重建精度分析Tab.4 Accuracy analysis of sculpture model reconstruction

表5 重建模型面片数量Tab.5 Number of reconstruction model patches

5 结 语

针对目前的点云三维重建的贪婪投影算法存在的重建耗时长,重构的模型存在表面粗糙、孔洞等问题,提出首先采用体像素网格滤波对点云进行下采样,然后采用移动最小二乘算法来对点云进行平滑及重采样,并且使用八叉树代替KD树进行近邻域搜索,最后使用基于移动最小二乘算法的点云法线估计的贪婪投影算法对点云进行重建,在保证重建效果的前提下,减少了重建的时间。通过实验验证,本文算法相较于泊松算法和传统的贪婪投影算法,耗时短,在模型表面的光滑度和孔洞修复上显示了更好的重建效果。但从实验结果可以看出,虽然改进算法对孔洞修复有了一定的改善,但还存在一些细小的孔洞,未能达到孔洞的完全修复,因此针对三维重建中孔洞完全修复有待进一步深入研究。