基于改进型B样条分层插值的汽车零件检测研究

宋艳芳,徐颖若,张继方

(1.同济大学汽车学院,上海 201800；2.河南工业职业技术学院汽车工程学院,河南 南阳 473000)

1 引 言

车辆零件加工装配技术日益成熟[1],在量产与自动化检测领域也取得了长足的发展,但随着零件表面复杂度和检测精度都越来越高[2],为了进一步满足复杂零配件三维结构的自动化检测,从而实现智能装配的最终目标,面向复杂结构汽车零件的自动检测技术的研究成为了热点。

国外工业发展起步较早,在工业自动化检测与控制方面具有领先地位,世界上第一台可编程机器人由美国斯坦福大学生产,目前已在汽车加工、零件装配等领域广泛应用。ABB公司设计的并联机器人成功应用于汽车零件加工中,其小巧的结构在车架内部零件安装过程中具有很好的适用性。Connolly[8]研究的传感式校正系统被应用于机器臂控制,在复杂零件结构检测中精度可优于400 μm。宝马公司推行的智能化汽车装配工程体系采用了虚拟现实与装配工艺流程相结合的设计思路,其中使用的数字孪生(Digital twin)技术就包含传感数据的获取,即自动检测系统。国内中科院自动化所研发的新松机器人就是自动化检测与控制有效结合的典型研究成果,其应用于汽车装配领域的布线工艺环节,具有很大的市场占比。浙江大学的装配技术国家重点实验室研发的虚拟装配软件模块,完成了检测数据与控制系统的数据对接,自动装配系统智能化发展提供了新的思路。同济大学汽车学院开展了汽车零件测量数据对仿真装配过程的校正研究,本文基于此基础针对汽车零件自动检测的扫描路径优化问题,给出了基于分层完成目标区域三次B样条插值的设计思路,构建了验证测试实验。

2 系统设计

2.1 系统组成

为了自动检测复杂面形汽车零件的表面并实现精确重构[15],使机械臂扫描路径更准确,实现为质检、安装等提供准确的修正数据,设计了自动检测系统,如图1所示。

图1 基于三次B样条分层插值的自动检测系统Fig.1 Automatic detection system based on cubic B-spline hierarchical interpolation

系统主要分为两大部分,一是计算分析部分,其中包括处理模块、扫描路径规划模块、分析算法模块；二是执行部分,其中包含机械臂控制模块、机械臂、光学探头。首先,处理模块通过数据采集卡读取由光学探头获取得到的测试件点云数据；然后,通过对测试数据进行三维重建获得测试件的位置与位姿信息；其次,在与工件数学模型对比的基础上,计算测试件实际位置与姿态和理论位置与姿态之间的差异；最后,结合测试获得的偏差数据信息,通过三次B样条分层插值算法完成对扫描路径的优化,从而实现优化自动检测扫描路径的目的。

2.2 工作机理

待测件点云的获取采用结构光配合双目视觉的方法实现,由线阵CCD完成待测区域光信号的采集,利用捕获靶标点信号完成目标的三维重构。设双目视觉系统的坐标系分别是P1和P2,如图2所示,当需要完成点云拼接时,将两个坐标系的数据进行对齐即可实现目标点云的组合。

图2 双目测量的工作机理示意图Fig.2 Schematic diagram of the working mechanism of binocular measurement

双目系统统一坐标系后设其主点为(u0,v0),两个相机的焦距与间距分别为F和D,在两个相机的像面位置上的点分别是P1(u1,v1)和P2(u2,v2)。则待测物坐标可以写成:

(1)

两个相机之间的坐标变换可以通过旋转矩阵和位移矩阵实现,两坐标系之间的变换符合以下矩阵变换规则:

(2)

式中,P表示位移矩阵;R为表示旋转矩阵,上标为选用坐标系,下标为目标坐标系,两个坐标系下的数据互换是可逆的。

3 三次B样条分层插值算法

3.1 传统B样条插值

机械臂的扫描路径常采用B样条曲线构成,由于装配等过程容易造成误差引入,简单的拟合曲线难以符合精度要求,故本文采用三次B样条,并且基于数据特征进行分层插值,从而实现根据测试数据特点进行扫描路径优化的目的。传统B样条曲线可以通过m个顶点和n个节点来控制,则定义B样条曲线为:

(3)

其中,i为n个节点中的第i个;节点值;j为m个顶点中的第j个;k为B样条的次数(本文中采用三次,即k=3);di为控制点数据;ui为节点矢量。

3.2 算法改进依据

由于汽车零件的表面结构复杂,在构建扫描曲线的时候如果不分类处理,在具有阶跃变化的位置很容易造成细节丢失,从而导致扫描精度降低。所以,采用数据分层的方式可以很好地解决诸如直角、棱边、孔洞等结构的点云数据拼接问题。数据分层的依据由测试面的连续程度决定,即采用测试曲面上待测点的曲率决定。这样分层的优势有两个:一是由曲率变化分层可以准确反映出曲面的形态与特征,二是由曲率计算法向量时可以直接为机械臂扫描路径优化提供位姿补偿信息。由此可见,基于曲率连续性的数据分层可以实现测量数据与扫描路径的数据关联,在此基础上,确定节点与顶点的矢量表达就能完成曲线插值重建。对于数据点qi而言,构造三次B样条曲线时要将首末数据点映射到B样条曲线的对应端点上,并且将数据点依次对应到段与段的连接点上,从而得到m段曲线。由此得到的三次B样条曲线将存在(n+1)个控制顶点dj。节点矢量的集合可以表示为:

再次，村落民俗志书写应兼顾村民立场，这是走出传统书写模式中主体“缺席”误区的关键。赵世瑜曾提出历史人类学应掌握一种“逆推顺述”的研究技术和叙事技巧，最近又将之视为一种观察历史的方法论，颇值得注意：

U=[u0,u1,…,un+k+1]

则其固支条件及定义域有:

u∈[u3,un+1]=[0,1]

其中,u0=u1=u2=u3=0,un+1=un+2=un+3=un+4=1。由此将节点矢量的构造过程在各个分层数据中进行遍历,从而获得每个数据分层中拟合曲线的节点矢量信息。

3.3 改进算法的实现

由于采用三次B样条,故k=3代入式(3),得到三次B样条函数:

(4)

然后将定义域[u3,un+1]中符合u∈[ui,ui+1]的节点依次导入方程后,有:

(5)

由此利用式(5)完成对控制顶点的解析,通过顶点方程的矩阵表达可以写成:

(6)

其中,a1、b1、c1为边界条件的首行非零系数；an-1,bn-1,cn-1为边界条件的末行非零系数；ai,bi,ci是中间行系数；d表示控制顶点(下标为顶点号)；e表示顶点矢量(下标为对应顶点)。所有系数可由节点矢量的差分量计算得到,有:

(7)

4 重建仿真分析

待测目标采用AtlaScan型双目扫描仪完成数据采集,该设备最大采样速率为900 /ms,分辨率最高为0.01 mm,仿真时根据设计需要的测试速度与重建精度,系统采样速率与精度选用500 /ms与0.05 mm。采集后的原始点云数据无法直接使用,因为目标点云与背景点云混叠在一起。所以需要先将数据导入MATLAB中完成杂散点滤波,滤波方法采用点云相邻域连通的方式实现。对于本测试中的零件而言,其曲面变化复杂程度并不高,所以只需要两个数据获取就能够得到完整的目标点云集合,然后对每一次获取的点云进行背景点云滤波,将目标点云数据保留后再完成三维目标的重建。

采用100 mm×100 mm扫描区域获取待测目标的点云数据,要求待测目标具有直角、棱边及孔洞等特征。由双目视觉系统获取待测目标结构的点云,导入MATLAB后,对杂散点进行滤波后可以得到目标的点云分布如图3(a)所示。通过点云数据的三次B样条分层插值完成对缺失信息的补偿,从而达到优化扫描路径的目的。在Qualify中,分别重建了无插值与经插值优化的重建效果,如图3(b)所示。

(b)重建数据图3 模拟汽车零件的点云与三维重建Fig.3 Point cloud and 3D reconstruction of simulated auto parts

将双目系统获取的基于靶标点的点云数据输入MATLAB后,利用边界滤波消除多余的噪声点,最终形成图3(a)中的点云数据集合,由此可以看出零件的大体外形轮廓。采用三角面片法将点云连通,从而构成目标的三维模型,重建得到零件的结构如图3(b)所示。在三维重建结构中抽取各个位置上的斜率信息与数模中对应位置上的斜率进行比较,就可以得到预设的扫描路径与实际目标位置之间存在的误差,故对测试得到的三维重建数据进行三次B样条分层插值,就能够将与数模之间的误差以补偿矩阵的形式给出,从而反馈控制调整机械臂轨迹,实现对系统扫描路径的优化。

5 实 验

实验中零件外形点云获取采用的是AtlaScan型双目扫描仪,系统采样速率为500 /ms,采样精度为0.05 mm,标准测试位置范围80 mm×80 mm。获取点云过程中利用数据连通特性完成目标点云与背景点云的区分,具体实现手段是对一个计算范围内的点云求解斜率均值,当相邻区域的点云斜率均值明显大于或小于其相邻域的计算结果时,认为该检测区域与相邻区域不同源,从而在已知目标表面的斜率范围的基础上,可以对所有点云数据区域进行遍历,最终将背景点云与杂散飞点等滤除掉。并且在完成数据运算时,可以通过降低已有目标点云数据总量的方法提高系统对目标重建的速度与边界。

为了验证本系统对扫描路径的优化效果,对上文中仿真分析的同一个零件进行扫描路径规划对比,零件尺寸范围80 mm×40 mm×40 mm,激光扫描范围为80 mm×80 mm,由此可见,在一个维向上仅需完成一次扫描即可获得零件在该维度上的投影数据。重建的曲面精度实际上会决定样件扫描时机械臂与样件表面的位姿关系,而不同的位姿关系计算得到的测试点位置是不同,也就是说,最终可以通过计算不同扫描路径条件下的位置偏移误差进行量化对比。

5.1 位置偏移误差的测量

将实际扫描得到的点云数据与数模点云数据进行点云匹配后,就可以计算两组数据之间的偏差,该偏差就是用于优化自动检测结构扫描路径的补偿信息。由于零件为三维结构,故采用测试点位置之间的绝对距离表征该偏差值,有:

(8)

其中,Δx、Δy、Δz分别表示测试点云数据与数模点云数据在x、y、z位置上的位置偏差量,则直接重建与采用三次B样条分层插值后重建的三坐标偏差数据及绝对距离偏差的计算结果如表1所示。

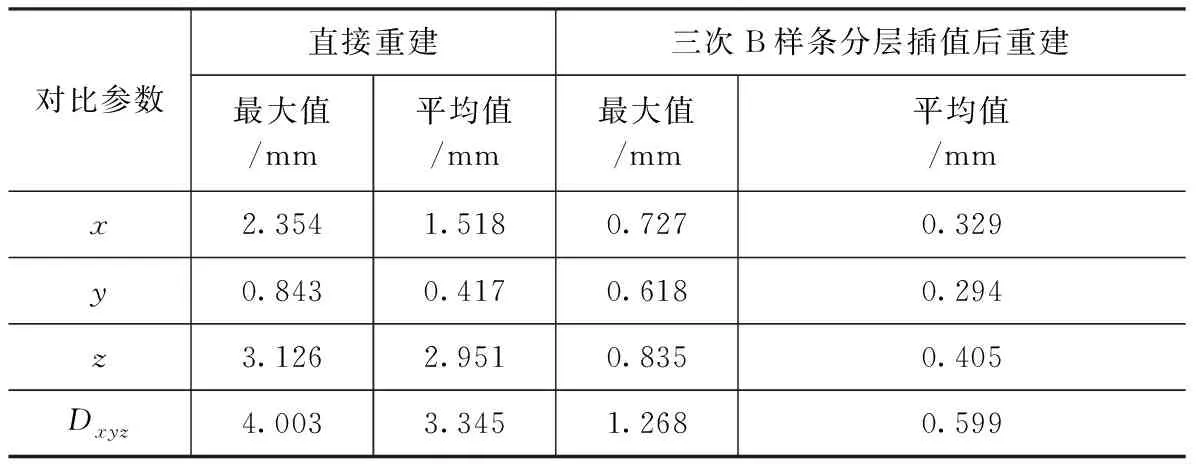
表1 偏差程度对比表Tab.1 Comparison table of deviation degree

由表1可知,优化后重建结果在x、y、z轴方向上的位置偏差的最大值和平均值都有所减小,减小程度约为原有测试值的1/3左右。分析认为,由于采用了三次B样条分层插值算法,通过实测数据点之间插值补偿的方式使拟合曲线更加接近真实值的。相比之下,由于在三个坐标轴方向上的位置偏差均有所改善,故其测试点位的绝对距离修正效果更为明显,约为优化前的1/4。

5.2 结果分析

根据算法对零件三维结构重建面形的误差校正,通过对误差数据的分布形式,给出了相应的自动检测扫描路径的规划结果。对300个样本点的测试偏差结果和基于此偏差结果的路径补偿归一化系数,如图4所示。从图4(a)中可以看出,测试点的绝对距离误差范围集中在0.2～0.8 mm之间,该数据可以为自动扫描路径的优化提供依据。也就是当绝对距离超过设定阈值时,通过程序判断该时刻x,y和z轴上正负值,并根据其正负关系(正值表示相对原路径点分离的程度,负值表示相对原路径点接近的程度)对扫描路径进行修正,修正参数由路径补偿归一化系数决定。而归一化系数如图4(b)所示,可以看出其分布趋势基本与Dxyz倒数接近,因为其就是用来补偿数模导出的扫描路径。综上所述,当采用本系统可以利用三次B样条分层插值算法对重建零件进行补偿,从而实现减小实际装配过程中扫描路径的误差。

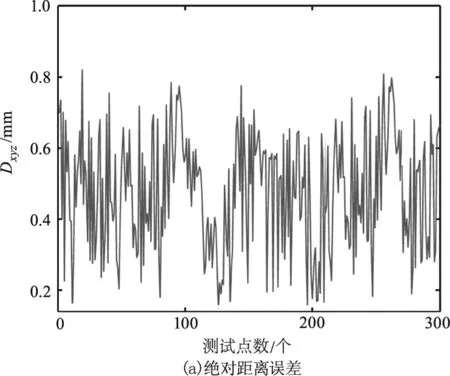
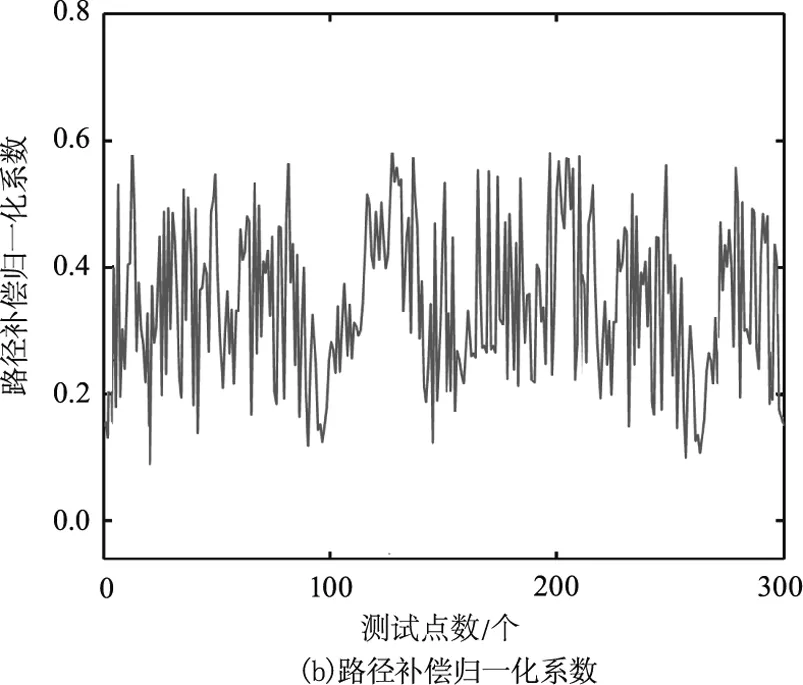
图4 测试点间的偏差程度与补偿系数Fig.4 The degree of deviation between the test points and the compensation coefficient

6 结 论

本文针对汽车零件自动检测过程中由于环境干扰会导致机械臂扫描轨迹与实际零件面形偏差增大的问题,提出了一种基于三次B样条分层插值算法,用于改善点云数据重建效果。在计算三个坐标轴方向上不同偏差程度的基础上,完成了基于测试点绝对距离的偏移误差判断,最终将包含该特征信息的数据以路径补偿归一化系数的形式对扫描轨迹进行修正,达到了优化扫描轨迹的目的。可见,该算法为自动检测的在线修正提出了新的思路。