部分相干径向偏振涡旋光焦场轨道角动量特性
贺 蕊,吕 宏,闫丽凝,庞令阳
(西安工业大学光电工程学院,陕西 西安 710021)
1 引 言
近年来,涡旋光束的轨道角动量在光学探测[1-2]、空间光通信[3-4]、光学微操纵[5]等领域拥有广泛的应用。径向偏振涡旋光束是一种偏振态沿径向变化的涡旋光束[6-7],兼具独特的偏振和相位分布特点,经过聚焦可能产生更新颖的轨道角动量性质,吸引了越来越多的关注。与完全相干光束相比,部分相干光束受湍流大气影响更小,光束的传输质量和性能更为优良[8-10],因此,开展部分相干的径向偏振涡旋光束聚焦轨道角动量特性研究,对其在空间目标探测等领域的应用有着潜在价值。
Guo等人[11]研究了部分相干径向偏振涡旋光束的相干长度和最大数值孔径角对焦场强度,相干度和偏振度的影响。田博等人[12]研究了聚焦光束形成的三维多点光俘获结构-光链。Shu等人[13]研究了聚焦部分相干径向偏振涡旋光束对瑞利粒子的辐射力与其相干长度、束腰宽度、拓扑电荷及物镜数值孔径之间的关系。Wang等人[14]研究了携带离轴涡旋阵列的径向偏振光束焦场内强度的空间重新分布对旋涡离轴距离和透镜数值孔径的依赖性。Zhang等人[15]研究了径向偏振涡旋光束的拓扑电荷对聚焦光场的调制。Xu等人[16]基于矢量衍射理论研究了径向偏振的多高斯谢尔模型涡旋光束经过高数值孔径透镜的聚焦特性。综上所述,目前关于部分相干的径向偏振涡旋光束聚焦研究中,轨道角动量特性相关报道还非常少见。
本文通过聚焦部分相干径向偏振涡旋光束到目标平面处,研究了焦场目标平面处的轨道角动量特性。根据部分相干及Richards-Wolf矢量衍射积分理论推导了光场及轨道角动量密度分布,讨论了光强和轨道角动量密度分布特性,同时,分析了入射光束的相干长度和聚焦透镜的数值孔径对纵向分量轨道角动量和轨道角动量密度分布的影响。
2 理论分析
偏振态沿径向变化,并且携带±l拓扑荷的径向偏振涡旋光束在源平面处的入射光场可以表示为:

(1)
式中,er为径向偏振矢量;w0为束腰半径。根据部分相干理论[17],得到部分相干径向偏振涡旋光束源平面处的交叉谱密度函数为:
(2)
其中,lc为相干长度。经过高数值孔径透镜聚焦,满足正弦近似条件r=fsinθ,因此,将式(2)改写为:
A(θ1,θ2,φ1,φ2)=4ercos(lφ1)cos(lφ2)
(3)
式中,cos(lφ1/2)为光场的角相位项。则入瞳处的振幅包络函数为:

(4)
根据Richards-Wolf矢量衍射积分理论[18],经过运算,得到柱坐标系下焦场目标平面处,部分相干径向偏振涡旋光束的光场分量为:
{[Jl+1(kr1sinθ1)-Jl-1(kr1sinθ1)]×
[Jl+1(kr2sinθ2)-Jl-1(kr2sinθ2)]}×
exp(ikzcosθ1)exp(-ikzcosθ2)dθ1dθ2
(-i)lsinθ1sinθ2cosθ1cosθ2sin(lφ1)sin(lφ2)×
{[Jl+1(kr1sinθ1)+Jl-1(kr1sinθ1)]×
[Jl+1(kr2sinθ2)+Jl-1(kr2sinθ2)]}×
exp(ikzcosθ1)exp(-ikzcosθ2)dθ1dθ2
(-i)l+1(sinθ1)2(sinθ2)2×cos(lφ1)cos(lφ2)×
[Jl(kr1sinθ1)×Jl(kr2sinθ2)]×exp
(ikzcosθ1)exp(-ikzcosθ2)dθ1dθ2
(5)

非傍轴近似条件下,任意一束单色光的时间平均轨道角动量密度可以表示为[19]:
(6)
其中,P为坡印廷矢量,r=xex+yey+zez。经过矢
量运算,得到各分量的轨道角动量密度分布分别为:
(7)
式中,ω为入射光束的频率;μ0为真空磁导率;c为光速,并且:
(8)
在光束横截面上对轨道角动量密度进行积分得到轨道角动量:
(9)
3 数值计算
图1所示为聚焦拓扑电荷|l|=1,|l|=2和|l|=3的部分相干径向偏振涡旋光束在目标平面处的总光强It(r,φ,z),以及各分量光强Ix(r,φ,z),Iy(r,φ,z),Iz(r,φ,z)的分布情况。以下所有数值计算中所选取的参数值为:激光波长λ=632.8 nm,束腰半径w0=1 cm,透镜焦距f=1 cm,折射率n=1.3。
从图1可以看出,目标平面处的光强沿着角向主要集中呈现在花瓣状图案内,且花瓣个数为2|l|,横向分量x和y的强度相比于纵向分量z都较弱,横向分量x的强度最弱。同时,光强中心存在空心型分布,横向分量x的空心程度较其余分量更大,比较同一分量的光强分布得出,空心大小随着拓扑荷绝对值的增大而变大。

图1 聚焦不同阶部分相干径向偏振涡旋光束目标平面处的光强分布(其他参数设置为:相干长度lc=1 cm,数值孔径NA=1)Fig.1 The light intensity distributions in the target plane of focusing partially coherent radially polarized vortex beams with different orders (The rest of parameter settings are:coherence length lc=1 cm,numerical aperture NA=1)
图2所示为|l|=1,|l|=2,|l|=3和|l|=4的部分相干径向偏振涡旋光束总光强以及各分量光强沿x轴的曲线分布图。如图2中的虚线显示,目标平面上,纵向分量的强度分布曲线接近于总的强度分布曲线。同时,与横向分量x的强度Ix相比,纵向分量强度Iz的光斑中心普遍具有较小的的空心尺寸,并且,随着拓扑荷绝对值的增加,所有光强中心的空心增大,这与上述讨论光强分布所得结果一致。其次,比较图2(a),(c)和图2(b),(d)可以发现,相位拓扑荷绝对值为奇数的光束总光强It和横向分量x的强度Ix存在不明显的非对称分布,而纵向分量强度Iz关于x=0保持对称,相位拓扑荷绝对值为偶数时,所有光强始终关于x=0对称分布。
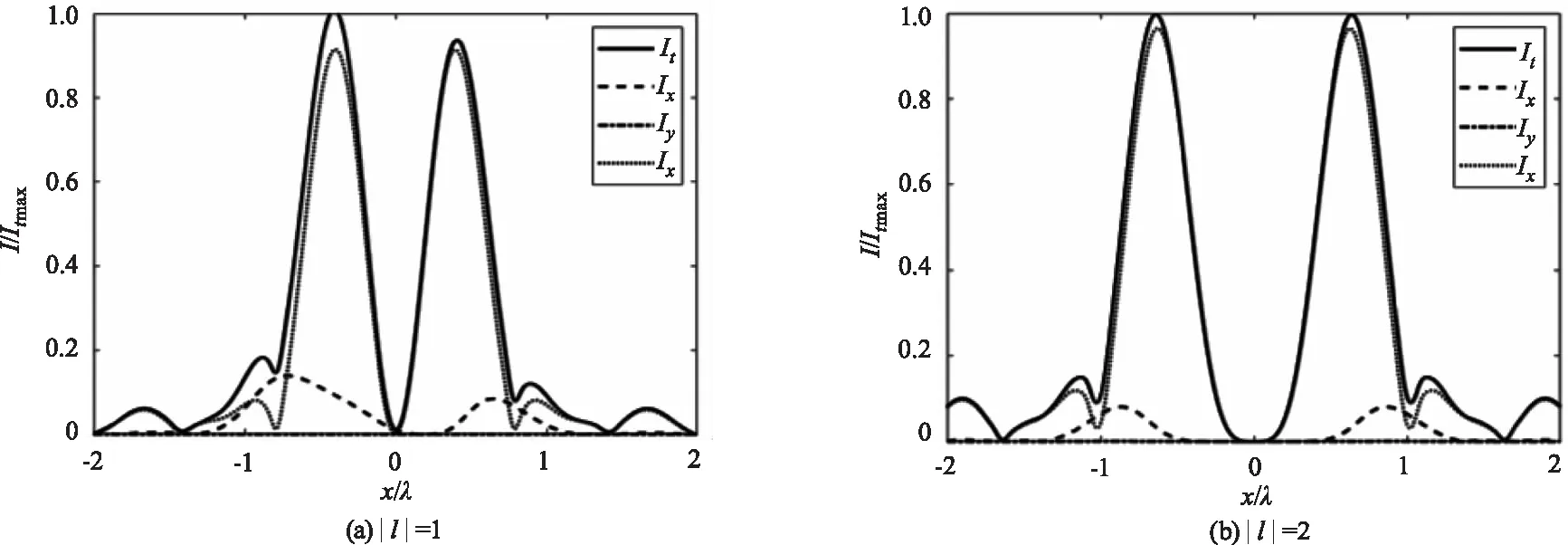

图2 不同阶部分相干径向偏振涡旋光束的光强分布曲线(所有光强已相对It归一化)Fig.2 The light intensity curves of partially coherent radially polarized vortex beams with different orders(all intensities have been relatively normalized toIt)
为了研究入射光束的相干长度及透镜的数值孔径变化对光强的影响,图3给出了拓扑荷|l|=2和|l|=3时,焦场目标平面处的总光强分布随着相干长度和数值孔径的变化情况。从图3(a),(c)可以看出,随着相干长度的增加,焦场平面处光强增大,光斑中心空心尺寸稍有减小,光强和空心现象在相干长度较小时变化程度更大,当相干长度增大至0.5 cm后,其变化不再对光强大小和光斑分布产生影响。此外,如图3(a)中的虚线显示,相干长度选择较小值会在一定程度上破坏偶数阶光束光强的对称分布。从图3(b),(d)可以看出,随着数值孔径的增大,目标平面处的光强没有明显变化,光斑中心空心尺寸略有减小。


图3 不同相干长度和数值孔径对部分相干径向偏振涡旋光束焦场目标平面处光强分布的影响Fig.3 The influence of different coherence lengths and numerical apertures on the intensity distributions for partially coherent radially polarized vortex beams in the focal field target plane
图4所示为结合公式(7)和(8)得到的|l|=1,|l|=2和|l|=3时,聚焦部分相干径向偏振涡旋光束在目标平面处各分量的轨道角动量密度分布情况。从图4可以看出,轨道角动量密度分布与光场分布类似,也集中呈现出花瓣状结构,花瓣个数同样为2|l|。不同之处在于,在轨道角动量密度分布中,只有横向分量x的轨道角动量密度较弱,横向分量y与纵向分量z的轨道角动量密度都较强。轨道角动量密度中心同样存在空心型分布,横向分量x的空心程度较其余分量更大,比较同一分量的轨道角动量密度分布得出,空心大小随着拓扑荷绝对值的增大而变大。此外,在同等参数设置下,拓扑荷绝对值更小的光束,目标平面处的轨道角动量密度整体数值反而更大。

图4 聚焦不同阶部分相干径向偏振涡旋光束目标平面处的轨道角动量密度分布Fig.4 The orbital angular momentum density distributions in the target plane of focusing partially coherent radially polarized vortex beams with different orders
图5所示为入射光束的相干长度和透镜的数值孔径改变对纵向分量轨道角动量密度分布的影响。从图5(a),(c)可以看出,纵向分量的轨道角动量密度随着相干长度的增加而增大,但增大程度在减弱,同样,当相干长度增大至0.5 cm后,相干长度的变化几乎不再影响轨道角动量密度分布。从图5(b),(d)可以看出,不同于数值孔径变化对光强影响很小,随着数值孔径的增大,纵向分量的轨道角动量密度也在变大,并且变化程度越来越大。

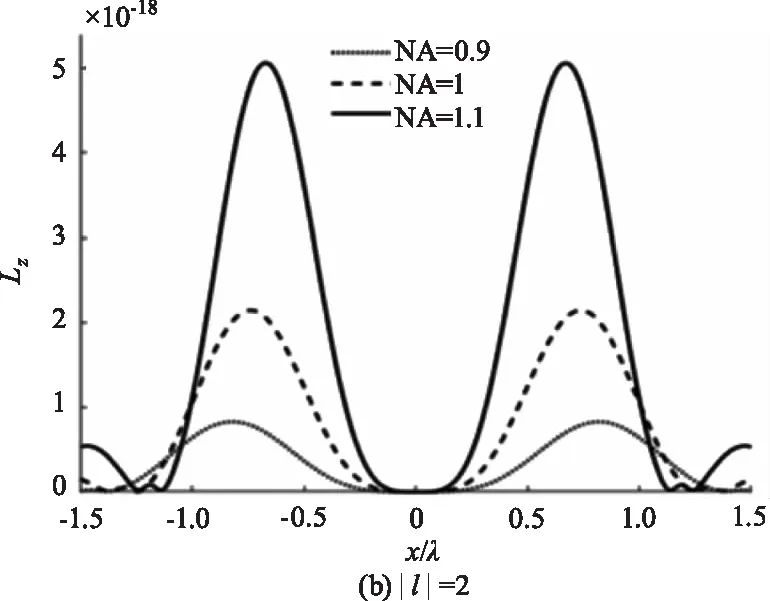


图5 不同相干长度和数值孔径对纵向分量焦场目标平面处轨道角动量密度分布的影响Fig.5 The influence of different coherence lengths and numerical apertures on the orbital angular momentum density distributions for the longitudinal component in the focal field target plane
最后,分析了入射光束相干长度和透镜数值孔径的变化对纵向分量焦场目标平面处轨道角动量的影响,结果如图6所示。如图6(a)所示,随着相干长度的增加,轨道角动量曲线迅速上升,当相干长度增大至0.5 cm后,轨道角动量的变化趋于平缓,即就是说,此后,相干长度的变化将不再影响纵向分量目标平面处的轨道角动量。从图6(b)可以看出,对于携带±l拓扑荷的部分相干径向偏振涡旋光束,透镜数值孔径较小时,纵向分量的轨道角动量随着数值孔径的增加缓慢增长,当增大至0.7后,也就是所谓的深聚焦情形,轨道角动量的增长程度越来越大。此外,可以发现,数值孔径在一定范围内变化时,l的值越小,纵向分量的轨道角动量反而更大,这与分析图4中NA=1时拓扑荷绝对值更小的光束,目标平面上的轨道角动量密度整体数值反而更大的结果相吻合。然而,随着数值孔径的持续增大,达到某一临界值后,l的值越大,目标平面处的轨道角动量就越大。例如,对于|l|=1的光束,当NA>1.1后,其轨道角动量小于|l|=2的光束,而在此之前,当NA=1时,其轨道角动量为4.2708×10-30,大于|l|=2时的轨道角动量3.7504×10-30,而对于|l|=2的光束,这一变化发生在NA>1.2后。这说明,当利用部分相干的涡旋光束进行焦场目标探测时,可以通过控制入射光束的相干长度和聚焦透镜的数值孔径来调整光束的轨道角动量。
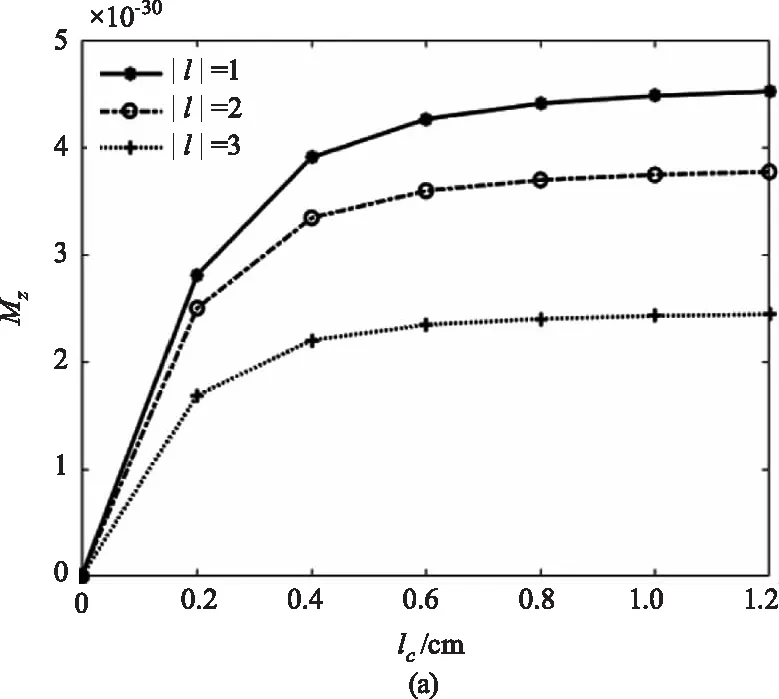
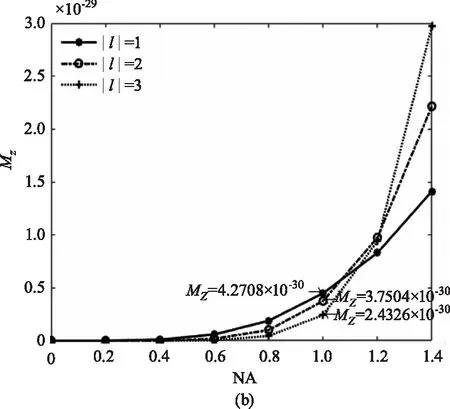
图6 纵向分量的轨道角动量随着相干长度lc和数值孔径NA的变化Fig.6 The orbital angular momentum of the longitudinal component changes with the coherence lengthlcand the numerical apertureNA
4 结 论
本文研究了通过聚焦部分相干径向偏振涡旋光束进行目标探测时,焦场目标平面处的强度和轨道角动量密度分布特性,以及入射光束的相干长度和聚焦透镜的数值孔径对纵向分量轨道角动量和轨道角动量密度分布的影响。结果表明:
(1)携带±l拓扑电荷的部分相干径向偏振涡旋光束焦场目标平面处的轨道角动量密度和强度分布均沿着角向主要集中呈现在花瓣状图案内,花瓣个数为2|l|。在强度分布中,横向分量的强度相比纵向分量都较弱,而在轨道角动量密度中,只有横向分量x的轨道角动量密度较弱,横向分量y与纵向分量的轨道角动量密度都较强。
(2)焦场目标平面处的光强,以及纵向分量的轨道角动量和轨道角动量密度都随着相干长度的增加而增大,当相干长度增大至0.5 cm后,相干长度的变化对其不再产生影响。
(3)随着数值孔径的增大,光强没有明显变化,纵向分量的轨道角动量密度和轨道角动量均变大,并且,变化程度在数值孔径大于0.7后越来越大。
研究成果对于将部分相干径向偏振涡旋光束的轨道角动量特性用于光学探测等领域具有一定的参考意义。

